埼玉県立高校入試2020年学校選択問題数学の問題と解説

埼玉県で行われた公立高校入試2020年（令和2年）度の学校選択問題の数学問題と解説です。
全部で大問5つありますが、問題の一部は一般入試と同じですので基本が大切だというところを見ておきましょう。
数学が上位校で合格点をとるために必要な科目なら手順に注目してみてください。

\(\,2020\,\)年度の埼玉県学校選択問題です。

⇒　2020年度埼玉県立高校入試学校選択問題の数学問題

学校選択問題を選択している人はある程度の基本ができているでしょうから解説は簡単にしておきます。
一般入試と重なる問題（\(\,\large{3}\,\),\(\,\large{4}\,\)）は一般入試で解説したページにリンクさせますのでご了承ください。

第１問小問集合

\(\,\large{1}\,\)は\(\,(1)\,\)から\(\,(9)\,\)まであります。

式の計算と方程式

\(\,(1)\,\)文字式の分数計算です。
　\(\hspace{10pt}\displaystyle \frac{1}{2}(3x-y)-\frac{4x-y}{3}\\
\displaystyle =\frac{3(3x-y)-2(4x-y)}{6}\\
\displaystyle =\frac{9x-3y-8x+2y}{6}\\
\displaystyle =\underline{　\frac{x-y}{6}　}\)

分子にはもともと（かっこ）が付いているのと同じことなので、
形が違っていても分数の扱いは同じです。

\(\,(2)\,\)直接代入しても答えは出ますが、
対称性から展開して代入した人が多いのかもしれません。
　\(\hspace{10pt}\displaystyle \left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\\
\displaystyle =1+\frac{1}{y}+\frac{1}{x}+\frac{1}{xy}　･･･①\\
\displaystyle =1+\frac{x+y}{xy}+\frac{1}{xy}　･･･②\)

これに代入しても良いのですが、同じ部分があるので別々に計算しておく方が早いです。
※
与式の対称性から基本対称式を先に計算しておいても良いくらいです。
基本対称式とは2つの文字の場合、\(\,x+y\,\)と\(\,xy\,\)のことです。

　\(\hspace{10pt} x+y\\
=(2+\sqrt{3})+(2-\sqrt{3})\\
=\color{red}{4}\)

　\(\hspace{10pt} xy\\
=(2+\sqrt{3})(2-\sqrt{3})\\
=4-3=\color{blue}{1}\)

これらを\(\,②\,\)に代入して
　\(\hspace{10pt}\displaystyle 1+\frac{x+y}{xy}+\frac{1}{xy}\\
\displaystyle =1+\frac{\color{red}{4}}{\color{blue}{1}}+\frac{1}{\color{blue}{1}}\\
=\underline{　6　}\)

\(\,①\,\)の段階で代入した人は少し焦り気味ですね。

\(\,(3)\,\)２次方程式の解を求めます。
\(\,(2)\,\)の対称式の求値問題にしても高校の数学\(\,Ⅰ\,\)でやり直す内容ですが、ここまでしておかなければ差がつかないのでしょう。

単純に展開して解の公式を使うか、文字を置きかえて解の公式を使うかのどちらかです。
（タスキガケ因数分解は\(\,2020\,\)年の段階で中学に戻る予定はありません。）

普通は置きかえるでしょう。

　\(\hspace{10pt}2(\color{red}{x-2})^2-3(\color{red}{x-2})+1=0\)

\(\,\color{red}{x-2}=t\,\)とすると

　\(\hspace{10pt}2\,t^2-3\,t+1=0\)

解の公式から
　\(\begin{eqnarray}\displaystyle
t&=&\frac{3\pm \sqrt{3^2-4\times 2\times 1}}{2\times 2}\\
&=&\frac{3\pm \sqrt{9-8}}{4}\\
&=&\frac{3\pm 1}{4}\\
&=&1\,,\,\frac{1}{2}
\end{eqnarray}\)

\(\,t=1\,\)のとき
　\(\,x-2=1\,\)　から　\(\,x=\underline{　3　}\,\)
\(\,\displaystyle t=\frac{1}{2}\,\)のとき
　\(\displaystyle \,x-2=\frac{1}{2}\,\)　から　\(\displaystyle \,x=\underline{　\frac{5}{2}　}\,\)

展開して解の公式とすると
　\(\begin{eqnarray}
2(x-2)^2-3(x-2)+1&=&0\\
2(x^2-4x+4)-3x+6+1&=&0\\
2x^2-8x+8-3x+6+1&=&0\\
2x^2-11x+15&=&0
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
x&=&\frac{11\pm \sqrt{11^2-4\times 2\times 15}}{2\times 2}\\
&=&\frac{11\pm \sqrt{121-120}}{4}\\
&=&\frac{11\pm 1}{4}\\
&=&\underline{　3\,,\,\frac{5}{2}　}
\end{eqnarray}\)

※会員の方でタスキガケ因数分解できるようになっている人は
　\(\begin{eqnarray}\displaystyle
2\,t^2-3\,t+1&=&0\\
(\,t-1\,)(\,2t-1\,)&=&0\\
t&=&1\,,\,\frac{1}{2}
\end{eqnarray}\)
となりますので確認しておいてください。

\(\,(4)\,\)普通の連立方程式です。
「方程式の解」とは、方程式に代入して成り立つ値なので、\(\,x,y\,\)の値を代入します。

　\( \begin{cases}
\hspace{7pt} a(3)+b(-4)=11\\ \\
\hspace{7pt} a(3)-b(-4)=-2
\end{cases}\)

見やすくします。

　\( \begin{cases}
\hspace{7pt} 3a-4b=11\\ \\
\hspace{7pt} 3a+4b=-2
\end{cases}\)

後はこの\(\,a,b\,\)の連立方程式を解くと、
　\(\displaystyle \underline{　a=\frac{3}{2}\,,\,b=-\frac{13}{8}　}\)

確率と反比例のグラフの性質

\(\,(5)\,\)さいころ2つの確率です。
さいころ2つは一般入試と同じですが、条件が違います。

　大きいさいころの出た目を\(\,\color{red}{a}\,\)
　小さいさいころのでためを\(\,\color{blue}{b}\,\)

このとき
　\(\hspace{10pt}\displaystyle \frac{1}{3}≦\frac{\color{red}{a}}{\color{blue}{b}}≦3\)
となる確率です。

さいころ2つは樹形図より表の方が早いです。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{blue}{1} & ○ & ○ & ○ & & & \\ \hline
\color{blue}{2} & ○ & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{blue}{3} & ○ & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{blue}{4} & & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{blue}{5} & & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{blue}{6} & & ○ & ○ & ○ & ○ & ○ \\ \hline
\end{array}\)

　\(\hspace{10pt}\displaystyle \frac{30}{36}=\underline{　\frac{5}{6}　}\)

ちょっとした分数計算だけで確率が求まるので考えることはありません。

考え方は2つあります。
一つはこの条件を満たす出方を数える方法。
もう一つはこの条件を満たさない出方を数える方法。

ただ、二つ目の方法は、一つ目の出方を調べて行くことで気がつくのが普通なので、
そのまま一つ目の方法を続けた方が早いです。
途中で\(\displaystyle \frac{a}{b}＜\frac{1}{3}\,,\,3＜\frac{a}{b}\)に考えを変える方がややこしいですしね。

また、調べ上げるときの文字の固定順位も\(\,a,b\,\)の二通りがあります。

最初に\(\,a\,\)を固定すると
　\(\,a=1\,\)のとき\(\,b=1,2,3\,\)
　\(\,a=2\,\)のとき\(\,b=1,2,3,4,5,6\,\)
　\(\cdots\)

最初に\(\,b\,\)を固定すると
　\(\,b=1\,\)のとき\(\,a=1,2,3\,\)
　\(\,b=2\,\)のとき\(\,a=1,2,3,4,5,6\,\)
　\(\cdots\)

どちらで調べ上げてもそれほど時間はかかりませんが、
いろいろ考えている方が時間がかかります。笑

さいころの出目も整数の\(\,6\,\)通りしかないので調べ上げた方が早いですね。
計算が速いかどうかは個人差があるのでなんとも言えませんが、
調べ上げるという気持ちで取り組めば答えまではそれほど差は出ません。

\(\,(6)\,\)は一般入試と同じなので解説は省略します。

⇒　2020年(令和2年)度埼玉県公立高校一般入試の数学問題と解説

反比例の関数は\(\,x\,\)の範囲にかかわらず変化の割合は一定ではありません。

円錐の表面積とデータの活用の代表値および標本

\(\,(7)\,\)一般入試と同じ円錐ですが求める値が表面積です。

⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

展開図ですね。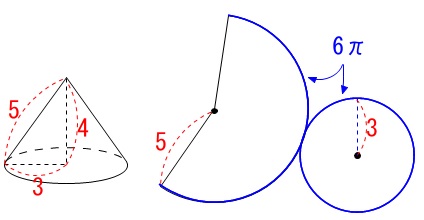表面積なので底面の面積を加えるのを忘れないで下さい。
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\pi \times 5+\pi\,(3)^2\\
=15\,\pi+9\,\pi\\
=\underline{　24\,\pi　}　(\,\mathrm{cm^2}\,)\)

\(\,(8)\,\)「平均値と中央値が等しい」という条件を満たす回数を求めます。

\(\,\mathrm{H}\,\)さんの成功回数\(\,\color{blue}{x}\,\)を除いた\(\,7\,\)人のデータを小さい順に並べると
　\(\hspace{10pt}5,6,7,\color{red}{8},8,9,10\)

\(\,\mathrm{H}\,\)さんの成功回数が何回であっても\(\,\color{red}{8}\,\)は中央値に関係してきます。

例えば
　\(\hspace{10pt}\color{blue}{x},5,6,\color{red}{7},\color{red}{8},8,9,10\)
　\(\hspace{10pt}5,6,7,\color{red}{8},\color{red}{8},9,10,\color{blue}{x}\)
となった場合でも、違う成功回数でも\(\,\color{red}{8}\,\)の左右どちらかに入ります。

\(\,8\,\)個のデータの中央値は小さい方から\(\,4\,\)番目と\(\,5\,\)番目の平均なので
　\(\hspace{10pt}\,\color{blue}{x}\,≦\,7\,\)のとき中央値は\(\,\displaystyle \frac{7+\color{red}{8}}{2}=7.5\,\)
　\(\hspace{10pt}\,\color{blue}{x}\,≧\,8\,\)のとき中央値は\(\,\displaystyle \frac{\color{red}{8}+8}{2}=8\,\)

平均値をこのどちらかにする\(\,x\,\)を求めるだけです。

分かっている\(\,7\,\)人のデータの合計は
　\(\hspace{10pt}5+6+7+8+8+9+10=\color{magenta}{53}\)
なので\(\,\mathrm{H}\,\)さんのデータ\(\,\color{blue}{x}\,\)を加えた\(\,8\,\)人の平均値は
　\(\hspace{10pt}\displaystyle \frac{\color{magenta}{53}+\color{blue}{x}}{8}=7.5　･･･①\)
または
　\(\hspace{10pt}\displaystyle \frac{\color{magenta}{53}+\color{blue}{x}}{8}=8　･･･②\)
を満たすはずです。

①のとき\(\,53+x=60\,\)なので
　\(\,x=7\,\)
②のとき\(\,53+x=64\,\)なので
　\(\,x=11\,\)

\(\,10\,\)回のフリースローで\(\,11\,\)回の成功はありません。

答え　\(\,\underline{　7　}　(\,回\,)\,\)

「回数」は整数なので調べて行っても答えは出ます。

\(\,7\,\)人のデータ合計が\(\,\color{magenta}{53}\,\)であることから、
\(\,\mathrm{H}\,\)さんの成功回数\(\,\color{blue}{x}\,\)を変えていくと、
平均値と中央値が一致するのは
　\(\,x=7\,\)のとき\(\,5,6,7,\color{red}{7},\color{red}{8},8,9,10\,\)
の場合の平均値
　\(\hspace{10pt}\displaystyle \frac{53+7}{8}=7.5\)
が中央値
　\(\hspace{10pt}\displaystyle \frac{7+8}{2}=7.5\)
と一致するときだけだと分かります。
　
方法は何でもいいです。
試験時間と満点を目指すことを考えるとあれこれ考えるより手を動かした方が早いでしょうけど。

それほど多くない具体的なデータの場合、
小さい順に並べるというのは最初にやっておいた方が良いですね。

\(\,(9)\,\)は一般入試と同じなので省略します。

⇒　2020年(令和2年)度埼玉県公立高校一般入試の数学問題と解説

理由は、「無作為に抽出している方法だから」という言葉が入っていれば良いです。

第２問作図と平行四辺形の証明

\(\,\large{2}\,\)は接線の作図と平行四辺形の証明の\(\,2\,\)問です。

\(\,(1)\,\)の接線の作図は良くある問題で、円の外にある点からの接線なので気をつけましょう。
\(\,(2)\,\)は一般入試と同じ図形で合同の証明までは同じで、その後に平行四辺形の成立を加えます。

円の外部からの接線の引き方

\(\,(1)\,\)円周上の点を通る接線は接点と中心と結んだ直線に対し、
接点から垂線を引けばすぐに終わります。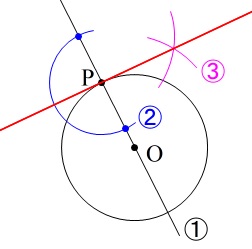

この問題のように円の外の点から接点を引く場合は、接点を正確に決めなくてはなりません。
※
「接線」とあれば、「接点の設定」は高校数学でも同じです。

作図で接線を引く場合は、円周角を利用します。

半径と接線は垂直に交わるので\(\,90°\,\)です。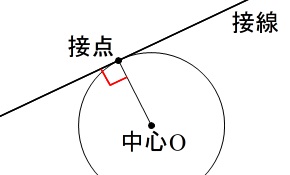これは直径に対する円周角になるので、
線分\(\,\mathrm{OP}\,\)を直径とする円を描くことを考えます。
（この時点でコンパスの針を刺す所が決まる。普通に考えても\(\,\mathrm{O}\,\)か\(\,\mathrm{P}\,\)しかないですけど。笑）
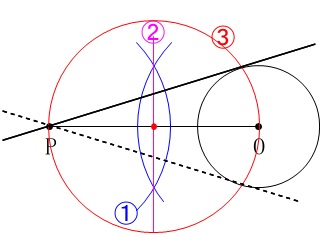円を描くには中心が必要です。
線分\(\,\mathrm{OP}\,\)の中点が中心になります。
　\(\,\color{blue}{①点\,\mathrm{O}\,と点\,\mathrm{P}\,から等しい円}\,\)を描き、
　\(\,\color{magenta}{②}\color{blue}{①の円}\color{magenta}{の2つの交点を結び}\,\)
（線分\(\,\mathrm{OP}\,\)の垂直二等分線です。）
　\(\color{red}{③}\color{magenta}{②}\color{red}{と\,\mathrm{OP}\,との交点を中心とする円}\)を描く。

最後に\(\,③\,\)の円と円\(\,\mathrm{O}\,\)との交点と点\(\,\mathrm{P}\,\)を結べば接線です。
（学校選択問題でこの説明は必要無かったですね。）

平行四辺形の証明

平行四辺形の成立条件は5つありますが、そのうち1つを言えば証明になります。

\(\,(2)\,\)一般入試では\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△CDF}\,\)を証明することが問題でした。ここでは、四角形\(\,\mathrm{AECF}\,\)が平行四辺形であることの証明です。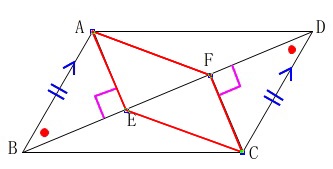
　\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△CDF}\,\)
であることは証明する必要がありますが一般入試問題で解説しています。

⇒　2020年(令和2年)度埼玉県公立高校一般入試の数学問題と解説

\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△CDF}\,\)なので対応する辺は等しく、
　\(\mathrm{AE}\,=\,\mathrm{CF}　･･･①\)
また、\(\,\mathrm{BD}\,\)⊥\(\,\mathrm{AE}\,\)　,　\(\,\mathrm{BD}\,\)⊥\(\,\mathrm{CF}\,\)なので
　\(\,\mathrm{AE}\,\)　∥　\(\,\mathrm{CF}\,　･･･②\)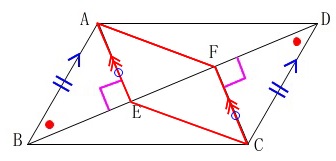①②から
　\(\color{blue}{\,1\,組の対辺が平行で等しい}\,　･･･\color{red}{③}\)
ので、四角形\(\,\mathrm{AECF}\,\)は平行四辺形である。
　
※\(\,\color{red}{③}\,\)について
「\(\,2\,\)辺が等しい」というときは「長さが等しい」という意味で使うので「等しい」だけですませていますが、
「長さが等しい」としても構いません。

第３,４問相似と比例式と関数の座標設定

\(\,\large{3}\,\)と\(\,\large{4}\,\)は一般入試と同じ問題なので省略します。

⇒　2020年度埼玉県公立高校一般入試の数学問題(第3,4問)と解説

\(\,\large{3}\,\)の\(\,(2)\,\)が一般入試問題と違うのは位置関係の図があるかないかだけです。

この程度の条件の抜き出しをしない人は、学校選択問題を受験することはやめておいた方が良いです。
厳しいことをいっているのではありません。
埼玉県の公立高校受験は問題がどうのこうのではなく、厳しいです。
パッと見た目に答えが出てくるほど単純な問題ばかりではありませんよ。

第５問立体の体積とねじれの位置と線分比

\(\,\large{5}\,\)は空間図形です。
　\(\,(1)\,\)立体の体積
　\(\,(2)\,\)ねじれの位置にある辺の本数
　\(\,(3)\,\)平面の切り口における線分比
ですが、気をつけるのは基本的なことだけど\(\,(2)\,\)です。
\(\,(3)\,\)は難しい問題ではありません。

立方体の体積と四角錐の体積

問題にある立体は、正四角錐と立方体で、
　\(\,\mathrm{PA=AB=2}\,\)
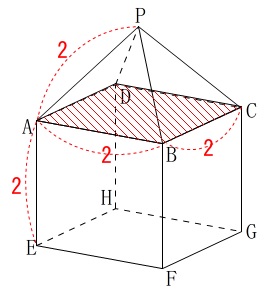これは最後まで同じ条件です。

\(\,(1)\,\)一度に計算すると計算式が横長になるので、
正四角錐と立方体に分けて計算します。

正四角錐の体積を求めるには、底面積と高さが必要です。
底面積はすぐに分かりますが、高さは点\(\,\mathrm{P}\,\)から底面となる四角形\(\,\mathrm{ABCD}\,\)に垂線を下ろします。

四角形\(\,\mathrm{ABCD}\,\)は正方形なので対角線の長さは
　\(\,\mathrm{AC=2\sqrt{2}}\,\)
対角線\(\,\mathrm{AB}\,\)と\(\,\mathrm{BD}\,\)の交点を\(\,\mathrm{O}\,\)とすると\(\,\mathrm{PO}\,\)が高さになり、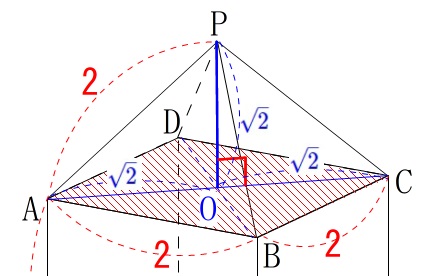
　\(\,\mathrm{AO=PO=\color{blue}{\sqrt{2}}}\,\)

四角錐部分の体積\(\,V_1\,\)は底面は正方形\(\,\mathrm{ABCD}\,\)なので
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times 2^2\times \color{blue}{\sqrt{2}}\\
&=&\color{magenta}{\frac{4\sqrt{2}}{3}}
\end{eqnarray}\)

立方体の体積\(\,V_2\,\)は1辺が\(\,\color{red}{2}\,\)なので
　\(V_2=2^3=\color{magenta}{8}\)

よって、求める立体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&V_1+V_2\\
&=&\underline{　\frac{4\sqrt{2}}{3}+8　}　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

通分はしてもしなくてもどちらでも良いです。

ねじれの位置にある辺の本数

\(\,(2)\,\)ねじれの位置については注意することが一つありますが、
立体の基本問題なので答えを先にお伝えします。
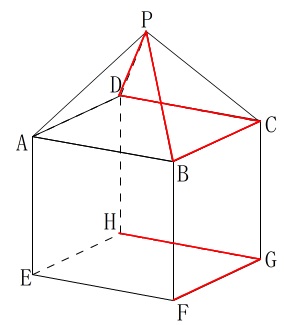　答え　\(\,\underline{　6　}　(\,本\,)\,\)

辺\(\,\mathrm{PC}\,\)もねじれの位置にありそうなのですが、

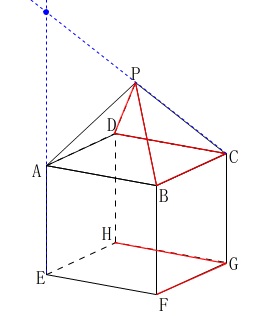
交わりもせず、平行でもない直線がねじれの位置になるので、
延長して交わりを持つ辺はねじれの位置とはいいません。

何故この問題を学校選択の最終問題に入れたのか？
もちろん、基本の確認でもありますが\(\,\mathrm{(3)}\,\)につながるように誘導してくれたのだとしたら、
昨年度とは確実に問題作成の意図が違います。

次で終わりです。
全体的に見ると昨年より易化して平均点は上がるでしょうけど良い問題構成ですね。

トップ校では差がつきにくくて、数学で差を付けるのは難しくなったけど、
ミスに気をつければ満点が狙えますね。

立体の中の線分比

立体を立体のまま考える、そんな高等技術必要ありません。
立体は平面図形の組み合わせでできているので、平面を抜き出せば良いだけです。

点\(\,\mathrm{E,B,D}\,\)を通る平面と辺\(\,\mathrm{PC}\,\)との交点が\(\,\mathrm{Q}\,\)なので、
四角形\(\,\mathrm{EBQD}\,\)を抜き出したいところですが、
求めたいのは線分\(\,\mathrm{PQ}\,\)と\(\,\mathrm{QC}\,\)の比なのでそれだけでは足りません。

ただ、点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P,A,E,G,C}\,\)が同じ平面にあることが分かればいいです。
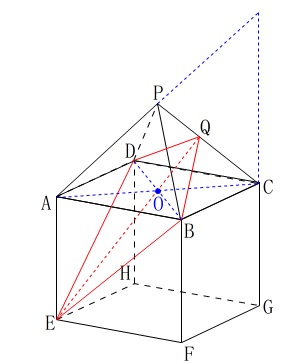\(\,(2)\,\)でねじれの位置にはないことの確認をしましたが、
\(\,\mathrm{AP}\,\)を延長すると\(\,\mathrm{GC}\,\)の延長と交わります。

\(\,\mathrm{EQ}\,\)は\(\,\mathrm{AC}\,\)の中点\(\,\mathrm{O}\,\)を通るので\(\,\mathrm{O}\,\)から交点まで\(\,\mathrm{EO}\,\)と同じ長さ伸びます。

立方体を2つ重ねると分かり易いですが、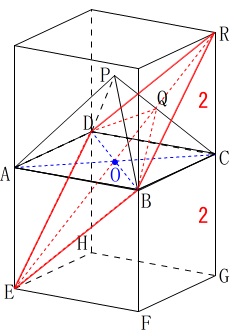
\(\,\mathrm{EQ}\,\)は\(\,\mathrm{EO}\,\)の延長にあるので、

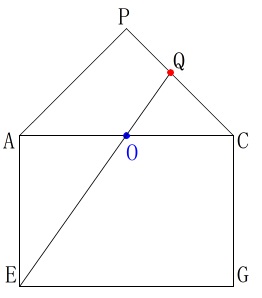
点\(\,\mathrm{Q}\,\)は平面\(\,\mathrm{PAEGC}\,\)上にあります。

ここまで来れば平面図形の問題になりますので、
長さを書き込んで平行線と相似で線分比が出ます。
が、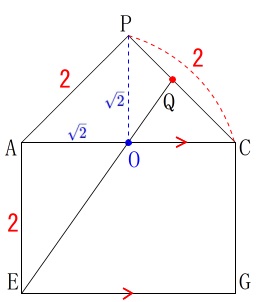相似がすぐには見つかりません。
補助線を入れますが、二通りあります。
\(\,\mathrm{CP}\,\)に平行な線を引いて、合同と相似を利用する方法が一つ。
しかしこれは回りくどいので、平面で切るときにイメージした立体の断面を見ます。
辺\(\,\mathrm{GR}\,\)は\(\,\mathrm{OP}\,\)に平行なので、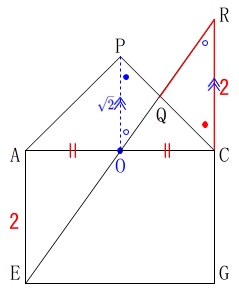
　\(\,\mathrm{△OQP}\,\)　∽　\(\,\mathrm{△RQC}\,\)
相似比は
　\(\hspace{10pt}\mathrm{OP:RC}=\mathrm{QP:QC}=\color{blue}{\sqrt{2}}:\color{red}{2}\)
よって、
　\(\hspace{10pt}\mathrm{PQ:QC}=\underline{　\sqrt{2}:2　}\)