ルートのついた平方根(無理数)と有理数の大小を比較する問題の解き方です。
無理数はルートが外せない場合があるので有理数との比較がやりにくいときがあります。
しかし、数の大小を比較するときにはコツがあります。
√（ルート）がついた無理数でも、整数や分数などと同じようにできるようになりますので確認しておきましょう。
有理数も根号（ルート）を使って表せる
ここでは、ルートのついた無理数の大小を比較していきますので、
整数や有理数にルートをつける付け方を覚えておかなければなりません。
といっても簡単なことで、ルートの外し方の逆の操作をすれば良いのです。
例えば、
\(\sqrt{2^2}=2\,,\,\sqrt{3^2}=3\)
となるように
\(2=\sqrt{2^2}=\sqrt{4}\)
\(3=\sqrt{3^2}=\sqrt{9}\)
のように\(\,2\,\)乗した数に\(\sqrt{ルート}\)を付ければいいだけです。
（分数でも同じようにできますが後で説明することにします。）
問題に入ります。
（１） \( \sqrt{78} , 9\)
（２） \(\sqrt{0.05} , 0.2\)
（３） \(-4\sqrt{3} , -3\sqrt{5}\)
問題１はこのページにはありません。
無理数の大小比較をするときのコツ
高校生でもわかっていない人多いですが、学校では教えないのでしょうかね。
数の大小比較の基本的な作業は、数字の世界をそろえてやることです。
整数なら整数どうしで、分数なら分数どうしで、小数なら小数どうしで、
そして、無理数は無理数どうしで比較すると分かり易いのです。
例えば、\(\,\sqrt{25}\,\)と\(\,\sqrt{24}\,\)では\(\,\sqrt{25}\,\)の方が大きいです。
これはわかりやすいでしょう？
根号の中が大きいほど無理数も絶対値は大きいです。
それさえわかれば、大小を比較するとき、
数直線上で右にあるほど大きい、
という基本通りみてあげればいいのです。
数直線は右に大きくなるようにとるのが普通なので、
数直線で右に来るほど大きくなるのです。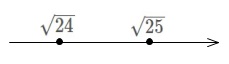
つまりルートがつく数字も数直線上で右に来る方が大きい、
ルートの中身が大きいほど全体が大きいということですね。
負の数、マイナスがつく場合は逆ですよ。
\(9=\sqrt{81}\) なので、\( \sqrt{78}\) との比較は簡単です。
数直線上で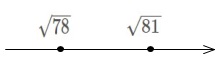
となっているので、
\(\sqrt{78} ＜ \sqrt{81}\)
ですが、これが答えではありません。
答えは問題に与えられた数で答えることを忘れないでください。
\(\underline{ \sqrt{78} ＜ 9 }\)
これが答えです。
数直線を書くという作業をするかしないか、大きな違いです。
これも数字の世界をそろえてあげます。
小数を \(\sqrt{ルート}\) の数に換えましょう。
\(0.2=\sqrt{0.2^2}=\sqrt {0.04}\)
なので、数直線上で表すと、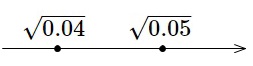
となりますので、
\(\sqrt {0.04} ＜ \sqrt{0.05}\)
です。
これも答えは、問題に与えられた数で答えましょう。
\(\underline{ 0.2 ＜ \sqrt{0.05} }\)
無理数も負の数は絶対値が大きいほど小さい
負の数は絶対値が大きいほど小さいということを思い出しましょう。
例えば \(\,-10\,＜\,-5\,\) です。
負の数で絶対値が大きいということは、数直線上で左にあるということです。
その前に、ルートの中身が違っていて大小の比較がしにくいので、ルートの中に数を入れてしまいましょう。
例えば、
\(\,2\,\)は\(\sqrt{ルート}\)の中に入れると\(\,2\,\)乗されるので\(\,\sqrt{4}\,\)になるように、
\( \color{red}{4}\sqrt{3}=\sqrt{\color{red}{4^2}\times 3}=\sqrt{16\times 3}=\sqrt{48}\)
\( \color{blue}{3}\sqrt{5}=\sqrt{\color{blue}{3^2}\times 5}=\sqrt{9\times 5}=\sqrt{45}\)
のように変形できます。
符号をつけて見ると
\(-4\sqrt{3}=-\sqrt{48}\)
\(-3\sqrt{5}=-\sqrt{45}\)
これを負の数として数直線上に並べると、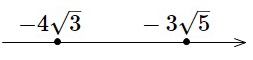
これから、
答えは\(\underline{ -4\sqrt{3}\,＜\,-3\sqrt{5} }\)となります。
負の数の大小は要注意ですね。
数の大小は世界をそろえて数直線上で比較する、というのは理解できましたか？
こういう基本作業をするかしないかで数学の成績は大きく変わりますよ。
特に数学が苦手、といっている人はね。
無理数と根号の使い方は復習しておきましょう。
⇒ 平方根と根号√(ルート)の使い方(ルートの外し方と符号の位置)
次は循環小数を見ておきます。
中学生の無理数の見分け方は簡単ですから軽く見ておいてください。
循環小数、これは高校でもやり直しますが、中学の数学にもありますよ。
出来ていない人多いですけど。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
