循環小数の表し方と有理数と無理数の見分け方をまとめて説明します。
小数には種類があります。
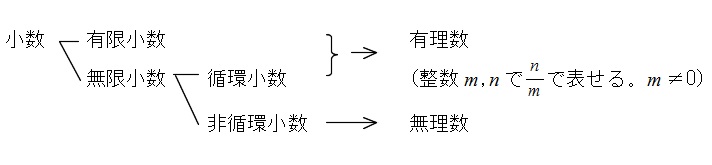
終わりのある有限小数と、繰り返した数字がずっと続く循環小数と、繰り返しのないずっと続く非循環小数です。
ここでは分数を循環小数に書き換える方法と、非循環小数である無理数と有理数との見分け方を練習問題の中で見てみましょう。
循環小数の表し方
小数には種類があります。
\(\,0.1\,\)や\(\,3.125\,\)といった終わりのある有限小数。
それに対して、\(\displaystyle \frac {1}{3}= 0.3333 \cdots\) といつまでも続く無限小数。
さらに無限小数には\(\,2\,\)種類あって、後で説明しますが、
一定の周期で数字が繰り返される循環小数と、
規則性のない数字が続く非循環小数に分かれます。
ここでは無限小数のうち、循環小数の表し方を問題の中で説明します。
（１）\(\displaystyle \frac{5}{12}\)
（２）\(\displaystyle \frac{4}{11}\)
（３）\(\displaystyle \frac{3}{7}\)
問題２まではこのページにはありませんので気にしないでください。
たとえば、
\(\displaystyle \frac {1}{3}= 0.3333 \cdots\)
といつまでも\(\,3\,\)を書いていたら終わりがありません。
無限に続くんだから終わるはずがありません。
そこで循環する数字の上に・を打って表します。
簡単で便利でしょう？
\(\displaystyle \frac {1}{3}= 0.\dot{\color{red}{3}}\)
これで終わりです。
\(\,\color{red}{3}\,\)が繰り返されるという意味です。
ただ、使い方にいくつか約束があるので、問題の中で見ていきましょう。
（１）先ずは普通に割り算して小数にします。
すると
\(\displaystyle \frac{5}{12}= 0.41\color{red}{ 6666 \cdots} \) と\(\,6\,\)だけが循環します。
このような場合は、\(\,\color{red}{6}\,\)の上に・を打ちます。
\(\displaystyle \frac{5}{12}=\underline{0.41\dot{\color{red}{6}}}\)
循環を始めた最初の数字の上に・を打ちます。
（２）これも割り算します。
\(\displaystyle \frac{4}{11}= 0.\color{red}{ 363636 \cdots}\) これは\(\,36\,\)が繰り返されているので、
\(\displaystyle \frac{4}{11}=\underline{0.\dot{\color{red}{3}}\dot{\color{red}{6}}}\)
とします。
見方によっては、\(\,63\,\)が繰り返しているように見えますが、
繰り返される最初の数字から・を打ちますから
\( 0.3\dot{6}\dot{3}\) としないように注意して下さい。
（３）
\(\displaystyle \frac{3}{7}=0.\color{red}{ 428571}\color{green}{ 428571}\color{red}{ \cdots}\) と\(\,428571\,\)が繰り返されています。
だからといって
\(\displaystyle \frac{3}{7}=0.\dot{4}\dot{2}\dot{8}\dot{5}\dot{7}\dot{1}\) とはしません。
繰り返される「最初と最後の数字の上」にだけ・を打てば良いのです。
つまり、
\(\displaystyle \frac{3}{7}=\underline{0.\dot{\color{red}{4}}2857\dot{\color{red}{1}}}\)
でOk.です。
逆に循環小数を分数に直す方法も知っておくと良いですがここでは扱いません。
興味がある人は高校の数学になりますが、
を参考にしておいてください。
まずは、循環小数の意味と、表し方を覚えましょう。
有理数と無理数の見分け方
無限小数には、循環するものとしないものがあります。
有限か、循環する小数を『有理数』といい、
分母分子とも整数（ただし、\(分母 \neq 0 \)）の分数で表せます。
\(\,(有理数)=\displaystyle \frac{q}{p}\hspace{4pt}(p\,,\,q:整数)\,\)
循環しない無限小数を『無理数』といいます。
では、無理数ってどういう数かというと、
たとえば \(\sqrt{2}=0.141421256 \cdots\) のような数です。
ルートが外れない数は循環しません。
「外れない」っていうのは \( \sqrt{4}=2\) のように根号が外せる数は、ルートがついていても無理数とはいわないということです。
\(\sqrt{ (根号) }\) の残る数が無理数、
と覚えていて良いのですが、、、例外があります。
円周率 \(\pi\) です。
\(\pi=3.141592653589793 \cdots\) と続くらしいです。
私は最初の\(\,2\,\)までしか覚えていませんが困ったことはありません。
他にも無理数はありますが、中学の間は
\(\color{red}{ \sqrt{ (根号) } の残る数と \pi}\)
が無理数と考えておいて良いです。
つまり \(\sqrt{ ルート }\) が外せたら有理数、
\(\sqrt{ ルート }\) が外せない数と \(\pi\) は無理数と判断すれば良いのです。
問題を見ておきましょう。
\(\displaystyle -\sqrt{16} , \pi , -\frac{2}{5} , \sqrt{6}\)
\(\displaystyle -\sqrt{11} , \sqrt{81} , \sqrt{0.04} , -\sqrt{\frac{121}{100}}\)
\( -\sqrt{16}= -4\)
\( \sqrt{81}= 9\)
\( \sqrt{0.04}= 0.2\)
\(\displaystyle -\sqrt{\frac{121}{100}}= -\frac{11}{10}\)
は有理数といえますので、
有理数： \(\displaystyle -\sqrt{16} , -\frac{2}{5} , \sqrt{81} , \sqrt{0.04} , -\sqrt{\frac{121}{100}}\)
無理数： \( \pi , \sqrt{6} , -\sqrt{11}\)
と分けることが出来ます。
分数全体に根号がついている場合は分母と分子に根号を分けてつければ良いので、
\(\displaystyle -\sqrt{\frac{121}{100}}=-\frac{\sqrt{11^2}}{\sqrt{10^2}} =-\frac{11}{10}\)
とこの場合は分母と分子が両方平方数なので根号をはずことができます。
ちなみに、\(3+\sqrt{5}\) のような
(有理数\(\,\pm\,\)無理数)も無理数
になります。
かけ算は？
計算結果によります。
結果に\(\sqrt{ルート}\)が残れば無理数です。
循環小数の表し方と有理数と無理数の見分け方、わかりましたか？
次はルートの計算です。
⇒ ルートのついた無理数のかけ算と割り算計算をはやくするコツ
無理数の意味がわかれば、文字式と同じように計算できるようになります。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
