2020年（令和2年）度に行われた北海道公立高校入試数学の問題と解説です。
標準問題と学校裁量問題は重なる問が4問あるのでまとめて解説しておきます。
いずれも5問構成ですが、裁量問題が意外と軽めだったのでそれほど詳しくする解説はありません。
ただ、数学の公式に当てはめるだけの問題ではないので差がつく原因ははっきりしています。
北海道公立入試の２０２１年度の数学の除外範囲がありますのでご確認下さい。
２０２１年（令和３年度）の出題範囲について
北海道では\(\,\mathrm{2021}\,\)年度公立高校入試の学力試験から数学では
「・相似な図形 ・円周角の定理 ・三平方の定理 ・標本調査」
を出題範囲から除外すると発表されています。
2020年度北海道公立高校入試(標準・裁量)数学の問題
\(\,2020\,\)年（令和\(\,2\,\)年）度に行われた北海道公立高校入試数学の問題です。
標準問題
学校裁量問題
標準問題の\(\color{black}{\fbox{2}}\)から\(\color{black}{\fbox{5}}\)が、
学校裁量問題の\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{4}}\)と同じになります。
2020年度北海道公立高校入試(標準・裁量)数学の解説
標準問題の\(\color{black}{\fbox{5}}\)までは普通に解説しますが、
学校裁量問題の\(\color{black}{\fbox{5}}\)は対象がそれなりの受験生だと思われるので、
解説を飛ばすところも出てきますので読み取って下さい。
標準問題の１の解説
\(\large{\color{black}{\fbox{1}}}\)
\(\color{black}{\fbox{1}}\)は式の計算から資料、関数、図形の小問集合です。
基本的な手順で進めて行けば、
手を止めるところはありません。
問\(\,1\,\)
式と計算です。
(1)
\(\hspace{10pt}-5\times 3\\
=\underline{ -15 }\)
正の数負の数の掛け算の結果（積）の符号は、
かけた負の数が奇数個の場合（\(\,-\,\)）です。
\(\hspace{10pt}-(5\times 3)\)
とも見られますが単項式なので
\(\hspace{10pt}(-5)\times 3\)
で良いですよ。
(2)
\(\hspace{10pt}9-6^2\\
=9-36\\
=\underline{ -27 }\)
累乗の\(\,6^2=6\times 6\,\)は掛け算です。
\(\hspace{10pt}9-6^2\\
=9-6\times 6\)
足し算引き算より掛け算が先です。
\(\,-36\,\)は数直線上で左に\(\,36\,\)移動します。
\(\,+9\,\)から左に\(\,36\,\)移動すると\(\,-2\,\)7なることを確認しておいて下さい。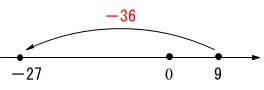
(3)
\(\hspace{10pt}\sqrt{14}\times \sqrt{7}-\sqrt{8}\\
=\sqrt{98}-\sqrt{8}\\
=\sqrt{2\times 7^2}-\sqrt{2^2\times 2}\\
=7\sqrt{2}-2\sqrt{2}\\
=5\sqrt{2}\)
とした人もいるでしょう。
素因数分解をしっかりやっているなら構いません。
\(2\,\underline{)\,98}\\
7\,\underline{)\,49}\\
\hspace{16pt}7\)
なれてきたら
\(\hspace{10pt}\sqrt{\color{red}{14}}\times \sqrt{7}-\sqrt{\color{blue}{8}}\\
=\sqrt{\color{red}{2\times 7}\times 7}-\sqrt{\color{blue}{2^2\times 2}}\\
=7\sqrt{2}-2\sqrt{2}\)
と素因数分解を先にすると早いです。
これくらいの簡単な引き算なら大した差はありません。
しかし、もっと計算量の多い場合でも通用するように無理数の足し算引き算は、
素因数分解を先にすると良いです。
割り算は約分利用ですよ。
計算は文字式も含めて全てに通用するように、
効率的な方法で通した方が結局は楽で早いです。
問\(\,2\,\)
絶対値の定義です。
絶対値は原点からの距離のことなので、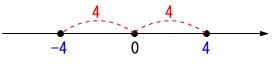
絶対値が\(\,4\,\)になるのは
\(\,\underline{ -4\,と\,+4 }\,\)
問\(\,3\,\)
代表値の1つ、中央値についてです。
中央値はデータを小さい、または大きい順に並べたとき、
真ん中の順位にある値のことです。
気温だけを順に並べると
\(\,21.6\,|\,22.2\,|\,24.2\,|\,\color{red}{25.9}\,|\,31.1\,|\,32.0\,|\,34.2\,\)
これをしない中学生、高校生が多いですが、
データを扱うときの基本です。
\(\hspace{10pt}\underline{ 25.9 ℃ }\)
問\(\,4\,\)
ねじれの位置にある辺です。
ねじれの位置とは
交わりもしない、平行でもない
ことです。
これは直線についてのことなので延長して交わる場合はねじれにはなりませんが、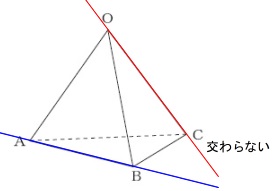
ここでは考えなくて良いですね。
答え \(\,\underline{ 辺\,\mathrm{OC} }\,\)
問\(\,5\,\)
比例です。
\(\hspace{10pt}y=ax\)
比例定数は無条件に求めに行きましょう。
\(\,x=2\,,\,y=-6\,\)を満たすので
\(\begin{eqnarray}
-6&=&a(2)\\
a&=&-3
\end{eqnarray}\)
比例の関数は
\(y=-3x\)
よって、\(\,x=-3\,\)のとき
\(\begin{eqnarray}
y&=&-3\times (-3)\\
&=&\underline{ 9 }
\end{eqnarray}\)
問\(\,6\,\)
図形の問題には違いないですが、
単なる三平方の定理の問題です。
直径に対する円周角は\(\,90^{\circ}\,\)になるから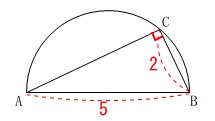
\(\,\mathrm{△ABC}\,\)は直角三角形なので、
三平方の定理から
\(\begin{eqnarray}
\mathrm{AC^2+BC^2}&=&\mathrm{AB^2}\\
\mathrm{AC^2}+2^2&=&5^2\\
\mathrm{AC^2}&=&25-4\\
&=&21\\
\mathrm{AC}&=&\pm \sqrt{21}
\end{eqnarray}\)
辺の長さなので\(\,\mathrm{AC\,＞\,0}\,\)だから
\(\hspace{10pt}\mathrm{AC}=\underline{ \sqrt{21} (\,\mathrm{cm}\,)} \)
\(\color{black}{\fbox{1}}\)は以上です。
ここまでは標準問題だけの問題になるので少し基本から説明しておきました。
次からは少し省略します。
標準問題の２（学校裁量問題の１）の解説
\(\large{\color{black}{\fbox{2}}}\)
\(\color{black}{\fbox{2}}\)は代入計算、確率、作図、方程式の小問集合です。
問\(\,1\,\)
代入するのは求値式（与式）を簡単にしてから、
最後に代入した方が楽な場合が多いです。
\(\hspace{10pt}3x(x+2y)+y(x+2y)\\
=(x+2y)(3x+y)\\
=\{(1)+2(-2)\}\{3(1)+(-2)\}\\
=(1-4)(3-2)\\
=(-3)\times (1)\\
=\underline{ -3 }\)
因数分解に気がつかなかったときでも、
ある程度は文字式の処理をしてからの方がミスは少なくなりますよ。
\(\hspace{10pt}3x(x+2y)+y(x+2y)\\
=3x^2+6xy+xy+2y^2\\
=3x^2+7xy+2y^2\\
=3(1)^2+7(1)(-2)+2(-2)^2\\
=3-14+8\\
=\underline{ -3 }\)
この問題はそのまま代入しても大した計算にならないだけです。
問\(\,2\,\)
マークと数字が違うカード\(\,4\,\)枚の並べ方です。
マークと数字があるのでややこしく感じますが、
数字だけ\(\,1,2,3,4\,\)とあって、
「奇数と偶数が交互になる並べ方」
と同じです。
問題の方が分かり易い表現をしてくれています。
並べ方は\(\,24\,\)通りしかないのでこの問題を難しいという人は
「解く気がない」
と判断されます。（少なくとも私はそう感じます。）
出題者は
「書き出せば分かるんだからあきらめるな！」
といいたいようですよ。
問題全体を通じて感じることです。
考え方は置き場を4つ作って、
「マークが同じにならないように左から並べていく」
という作業だけです。
\(○\,○\,○\,○\)
一番左は何でも良いので\(\,\color{red}{4}\,\)通り。
\(\color{red}{4}\times\,○\,○\,○\)
\(\,2\,\)番目は\(\,1\,\)番目と違うマークの数字はどちらでも良いので\(\,\color{blue}{2}\,\)通り。
\(\color{red}{4}\times\,\color{blue}{2}\times \,○\,○\)
\(\,3\,\)番目は\(\,2\,\)番目と違うマークの残りの\(\,\color{magenta}{1}\,\)通り。
\(\color{red}{4}\times\,\color{blue}{2}\times \,\color{magenta}{1}\times\,○\)
最後は必ず残りの\(\,1\,\)通り。
\(\color{red}{4}\times\,\color{blue}{2}\times \,\color{magenta}{1}\times\,1\)
よって、
\(\hspace{10pt}\underline{ 8 通り }\)
書き出してみます。
\(\begin{array}{|c|c|c|c|} \hline
\,♠\mathrm{A}\, & \,\color{red}{♦\mathrm{A}}\, & \,♠2\, & \,\color{red}{♦2}\, \\ \hline
\,♠\mathrm{A}\, & \,\color{red}{♦2}\, & \,♠2\, & \,\color{red}{♦\mathrm{A}}\, \\ \hline
\,♠2\, & \,\color{red}{♦\mathrm{A}}\, & \,♠\mathrm{A}\, & \,\color{red}{♦2}\, \\ \hline
\,♠2\, & \,\color{red}{♦2}\, & \,♠\mathrm{A}\, & \,\color{red}{♦\mathrm{A}}\, \\ \hline
\,\color{red}{♦\mathrm{A}}\, & \,♠\mathrm{A}\, & \,\color{red}{♦2}\, & \,♠2\, \\ \hline
\,\color{red}{♦\mathrm{A}}\, & \,♠2\, & \,\color{red}{♦2}\, & \,♠\mathrm{A}\, \\ \hline
\,\color{red}{♦2}\, & \,♠\mathrm{A}\, & \,\color{red}{♦\mathrm{A}}\, & \,♠2\, \\ \hline
\,\color{red}{♦2}\, & \,♠2\, & \,\color{red}{♦\mathrm{A}}\, & \,♠\mathrm{A}\, \\ \hline
\end{array}\)
マークと数字を書こうとすると大変なので
\(\,\mathrm{スA\,,\,ス2\,,\,ダA\,,\,ダ2}\,\)
でも良いですし、
カードの左から\(\,1,\color{red}{2},3,\color{red}{4}\,\)とすると
\(\begin{array}{|c|c|c|c|} \hline
\,1\, & \,\color{red}{2}\, & \,3\, & \,\color{red}{4}\, \\ \hline
\,1\, & \,\color{red}{4}\, & \,3\, & \,\color{red}{2}\, \\ \hline
\,3\, & \,\color{red}{2}\, & \,1\, & \,\color{red}{4}\, \\ \hline
\,3\, & \,\color{red}{4}\, & \,1\, & \,\color{red}{2}\, \\ \hline
\,\color{red}{2}\, & \,1\, & \,\color{red}{4}\, & \,3\, \\ \hline
\,\color{red}{2}\, & \,3\, & \,\color{red}{4}\, & \,1\, \\ \hline
\,\color{red}{4}\, & \,1\, & \,\color{red}{2}\, & \,3\, \\ \hline
\,\color{red}{4}\, & \,3\, & \,\color{red}{2}\, & \,1\, \\ \hline
\end{array}\)
色も分けなくていいです。
\(\,1,2,①,②\,\)
で十分見分けがつきます。
普段から書き出そうとしていれば、
自分なりに分かり易い表し方に気がつくようになります。
もちろん、樹形図で良いですよ。
あ、ここは対策じゃ無くて解説なので説明は適当で良いんだった。笑
長くなるので適当にします。
問\(\,3\,\)
作図です。
\(\,30^{\circ}\,\)は\(\,60^{\circ}\,\)の半分なので
正三角形を作り、角の二等分線を引けば点\(\,\mathrm{P}\,\)が見つかります。
辺\(\,\mathrm{BC}\,\)を\(\,1\,\)辺とする正三角形を描き、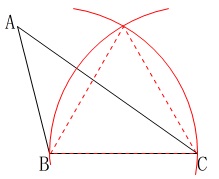
（交点が正三角形のもう一つの頂点です。）
角の二等分線を引き、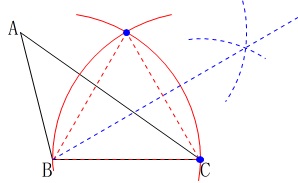
辺\(\,\mathrm{AC}\,\)との交点が点\(\,\mathrm{P}\,\)です。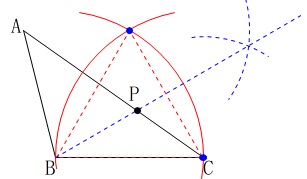
正三角形を作ったので、
等しい\(\,2\,\)辺を利用していたら角の二等分線です。
「角の二等分線を使ってます。」
のアピールとしては正答例のようにもう一手間加えても良いかもしれません。
しかし、一度長さを\(\,\mathrm{BC}\,\)で固定したコンパスをそのまま使うなら、
平行四辺形（ひし形）を作った方が早いですね。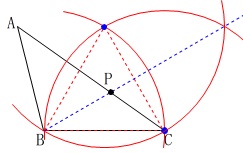
コンパスの針を刺す位置を間違わなければそれほど気にする問題でもありません。
問題は\(\,30^{\circ}\,\)が\(\,60^{\circ}\,\)の半分で、
正三角形を描きにいけるかどうかです。
問\(\,4\,\)
文字式の利用と方程式です。
北海道旗が問題に使われるのは北海道だけです。笑
これは日本国旗（日の丸）でも同じ問題ができます。
対称性のある図形なのでいろいろな問題が想定できるのですが、
資料から分かることは比例関係だけです。
\(\color{red}{\fbox{ 資料の内容 }}\)
道旗の縦と横の長さの比は\(\,2:3\,\)
道章の直径は道旗の縦の長さの\(\displaystyle \,\frac{5}{7}\,\)倍
言い換えると
道章の直径と道旗の縦の長さの比は\(\,5:7\,\)
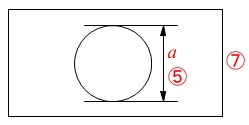
(1)
道章の直径を\(\,a\,\)とすると道旗の縦の長さ\(\,x\,\)は、
\(\begin{eqnarray}\displaystyle
a:x&=&5:7\\
5x&=&7a\\
x&=&\underline{ \frac{7\,a}{5} (\,\mathrm{cm}\,)}
\end{eqnarray}\)
これは比例式を立てなくても
\(\hspace{10pt}\displaystyle \underline{ \frac{7}{5}a (\mathrm{cm})}\)
としても良いです。
(2)
道旗の面積で方程式を立てます。
道旗の縦横の比が\(\,2:3\,\)なので、
縦と横の長さを\(\,2x\,,\,3x\,\)としたいところですが、
問題に縦を\(\,x\,\)とする指定があります。
道旗の縦の長さが\(\,x\,\)なので横の長さを\(\,y\,\)とすると
\(\begin{eqnarray}\displaystyle
2:3&=&x:y\\
2y&=&3x\\
y&=&\frac{3}{2}\,x
\end{eqnarray}\)
から横の長さは\(\displaystyle \,\frac{3}{2}x\,\)となります。
面積が\(\,\mathrm{9000\,cm^2}\,\)なので方程式は
\(\hspace{4pt}\displaystyle \underline{ x\times \frac{3}{2}\,x=9000 }\)
この方程式を解くと
\(\begin{eqnarray}\displaystyle
x\times \frac{3}{2}\,x&=&9000\\
3x^2&=&18000\\
x^2&=&6000\\
x&=&\pm \sqrt{6000}\\
&=&\pm 20\sqrt{15}
\end{eqnarray}\)
長さなので\(\,x\,＞\,0\,\)だから
\(\hspace{10pt}x=\underline{ 20\sqrt{15} (\,\mathrm{cm}\,)}\)
標準問題の３（学校裁量問題の２）の解説
\(\large{\color{black}{\fbox{3}}}\)
\(\color{black}{\fbox{3}}\)は倍数、公倍数の問題です。
ただし、難しい整数論を聞いているのでは無く、
「カレンダーを見て取れますか？」
「うるう年って知ってますか？」
と聞いているような問題です。
問\(\,1\,\)
毎年\(\,9\,\)月と\(\,12\,\)月は\(\,1\,\)日（初日）が同じ曜日である理由を考えます。
同じ曜日というのはその日から\(\,7\,\)日後に来ますので、
\(\,7\,\)の倍数日後は同じ曜日です。
つまり、\(\,n\,\)日後が同じ曜日というのは
\(\,n\,\)が\(\,\color{red}{7}\,\)の倍数のとき
ということです。
\(\color{black}{\fbox{ ア }}\) \(\,\underline{ 7 }\,\)
\(\,9\,\)月は\(\,30\,\)日
\(\,10\,\)月は\(\,31\,\)日
\(\,11\,\)月は\(\,30\,\)日
これは毎年変わりません。
（変わるとすれば\(\,2\,\)月だけです。）
このことから\(\,12\,\)月\(\,1\,\)日は、
\(\begin{eqnarray}n&=&30+31+30\\
&=&\color{red}{91}\end{eqnarray}\)
なので、\(\,9\,\)月\(\,1\,\)日から\(\,91\,\)日後になります。
\(\color{black}{\fbox{ イ }}\) \(\,\underline{ 91 }\,\)
※
\(\,9\,\)月\(\,1\,\)日から
\(\,1\,\)日後が\(\,9\,\)月\(\,2\,\)日
\(\,2\,\)日後が\(\,9\,\)月\(\,3\,\)日
\(\cdots\)
\(\,30\,\)日後が\(\,10\,\)月\(\,1\,\)日
となることを確認しておきましょう。
\(\,30\,\)日後が\(\,9\,\)月\(\,30\,\)日ではありません。
\(\,n=91\,\)となる\(\,91\,\)日後は
\(\hspace{10pt}91=7\times \color{red}{13}\)
で\(\,7\,\)の倍数になっているので同じ曜日になるということです。
\(\color{black}{\fbox{ ウ }}\) \(\,\underline{ 13 }\,\)
問\(\,2\,\)
\(\,1\,\)年間のすべての日の曜日が同じになる年を探します。
\(\,2020\,\)年から\(\,2100\,\)年までなので、
\(\,81\,\)年分を調べれば終わります。
調べました。
答え \(\,\underline{ 2048年 2076年 }\,\)
【解説】
うるう年は\(\,1\,\)年が\(\,366\,\)日なので
\(366=7\times 52\color{red}{+2}\)
で翌年は曜日が\(\,2\,\)日進んで\(\,1\,\)月\(\,1\,\)日が始まります。
うるう年でない年は\(\,1\,\)年が\(\,365\,\)日なので
\(365=7\times 52\color{blue}{+1}\)
で翌年は曜日が\(\,1\,\)日進んで\(\,1\,\)月\(\,1\,\)日が始まります。
\(\,2100\,\)年はうるう年ではありませんが、(※※)
\(\,2096\,\)年までは\(\,4\,\)年おきにうるう年がきますので、
\(\,2020\,\)年から\(\,4\,\)年間ごとに\(\,+5\,\)曜日が進みます。
\(\begin{array}{|c|c|} \hline
年度 & 曜日 \\ \hline
2020 & \color{red}{水} \\ \hline
2024 & 月 \\ \hline
2028 & 土 \\ \hline
2032 & 木 \\ \hline
2036 & 火 \\ \hline
2040 & 日 \\ \hline
2044 & 金 \\ \hline
2048 & \color{red}{水} \\ \hline
\end{array}\)
うるう年から次のうるう年までの\(\,4\,\)年間で\(\,+5\,\)曜日が進むので、
\(\,7\,\)の倍数になるのはうるう年が\(\,7\,\)回過ぎて、
\(\,8\,\)回目の年の初日が同じ曜日になります。
この次のうるう年で同じ曜日で始まるのは、
\(4\times 7=28\)年後
なので
\(\hspace{10pt}2048+28=2076年\)
この\(\,28\,\)年後は\(\,2100\,\)年までにはないのでここまでです。
※※
うるう年は西暦で\(\,4\,\)で割れる年度になりますが、
\(\,100\,\)で割れる年度はうるう年では無くしてズレを調整します。
なので\(\,2100\,\)年はうるう年ではありません。
さらに\(\,400\,\)で割れる年度はうるう年に戻りますが、
これを読んでいる人は生きていないので関係ありません。
（ズレの調整方法が変わる可能性はあります。）
カレンダーが\(\,\mathrm{7}\,\)日周期であることから規則性を見れば、
小学生でも答えを出せる問題です。
時間との関係もありますが捨てる問題ではありません。
標準問題の４（学校裁量問題の３）の解説
\(\large{\color{black}{\fbox{4}}}\)
\(\color{black}{\fbox{4}}\)は関数の座標設定問題です。
座標設定問題にしては容易なのでここで時間を稼げば良かったのですが、
会場での判断は難しいかもしれません。
当会の『最大得点獲得法』を読んで試験慣れしておくと良いです。
\(\color{black}{\fbox{4}}\)全体の条件です。
関数\(\displaystyle \,①：y=\frac{1}{2}\,x^2\,\)
関数\(\displaystyle \,②：y=-\,x^2\,\)
\(\,\mathrm{A}\,\)は\(\,①\,\)上の点で\(\,x\,\)座標は\(\,t\,\)で\(\,t\,＞\,0\,\)
\(\,\mathrm{B}\,\)は\(\,y\,\)軸を軸として\(\,\mathrm{A}\,\)と対称な点
\(\,\mathrm{C}\,\)は\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じで\(\,②\,\)上の点
\(\,\mathrm{D}\,\)は\(\,②\,\)上の点で\(\,x\,\)座標は負
座標を\(\,t\,\)を用いて表しましょう。
（座標設定です。）
\(\,\mathrm{A}\,\)は\(\,①\,\)上の点なので
\(\hspace{10pt}\displaystyle \mathrm{A}\,\left(\,t\,,\,\frac{1}{2}\,t^2\,\right)\)
\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)軸対称なので
\(\hspace{10pt}\displaystyle \mathrm{B}\,\left(\,-t\,,\,\frac{1}{2}\,t^2\,\right)\)
\(\,\mathrm{C}\,\)は\(\,\mathrm{A}\,\)と\(\,x\,\)座標と同じで\(\,②\,\)上の点なので
\(\hspace{10pt}\mathrm{C}\,(\,t\,,\,-t^2\,)\)
問\(\,1\,\)
四角形\(\,\mathrm{ABCD}\,\)が長方形にあるときの\(\,\mathrm{D}\,\)の座標です。
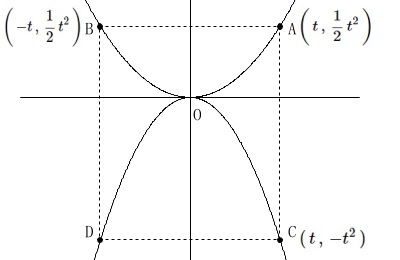
長方形なので\(\,y\,\)軸を軸として\(\,\mathrm{C}\,\)と対称になれば良いので
（\(\,\mathrm{B}\,\)と\(\,x\,\)座標を同じにする、としても同じです。）
\(\hspace{10pt}\mathrm{D}\,\underline{ (\,-t\,,\,-t^2\,) }\)
問\(\,2\,\)
\(\,\mathrm{C}\,\)を通り傾き\(\,-3の\,\)直線の式を求めます。
\(\,t=4\,\)のとき\(\,\mathrm{C}\,\)は
\(\hspace{10pt}(\,4\,,\,-16\,)\)
なので、\(\,\mathrm{C}\,\)を通り傾きが\(\,-3\,\)の直線の切片は
\(\hspace{10pt}y=-3x+b\)
に代入して、
\(\begin{eqnarray}
-16&=&-3\times (4)+b\\
b&=&-4
\end{eqnarray}\)
よって、
\(\hspace{10pt}\underline{ y=-3x-4 }\)
問\(\,3\,\)
\(\,2\,\)点\(\,\mathrm{B,C}\,\)を通る直線の傾きが\(\,-2\,\)となるときの\(\,\mathrm{A}\,\)を求めます。
\(\,\mathrm{B,C}\,\)を通る直線の傾きは\(\,\mathrm{B,C}\,\)の変化の割合になるので
\(\begin{eqnarray}\displaystyle
\frac{\color{red}{-t^2-\displaystyle \frac{1}{2}\,t^2}}{\color{blue}{t-(-t)}}&=&-2\\
\frac{\color{red}{-\displaystyle \frac{3}{2}\,t^2}}{\color{blue}{2t}}&=&-2\\
\color{red}{-\frac{3}{2}\,t^2}&=&-2\times (\color{blue}{2t})\\
-\frac{3}{2}\,t^2&=&-4t\\
3t^2&=&8t\\
3t^2-8t&=&0\\
t(3t-8)&=&0\\
t&=&0\,,\,\frac{8}{3}
\end{eqnarray}\)
\(\,t\,＞\,0\,\)なので\(\displaystyle \,t=\frac{8}{3}\,\)。
このとき\(\,\mathrm{A}\,\)の\(\,y\,\)座標は
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \left(\frac{8}{3}\right)^2\\
&=&\frac{1}{2}\times \frac{64}{9}\\
&=&\frac{32}{9}
\end{eqnarray}\)
なので
\(\hspace{10pt}\displaystyle \mathrm{A}\underline{ \,\left(\,\frac{8}{3}\,,\,\frac{32}{9}\,\right) }\)
「変化の割合」は
\(\hspace{10pt}\displaystyle \frac{ \color{red}{y\,の増加量} }{ \color{blue}{x\,の増加量} }\)
であり、直線の傾きと同じです。
標準問題の５（学校裁量問題の４）の解説
\(\large{\color{black}{\fbox{5}}}\)
\(\color{black}{\fbox{5}}\)は平面図形の角度の問題です。
相似の証明もありますが、辺の長さはないので角度だけの問題になります。
条件です。
\(\,\mathrm{∠BAE=∠BCD=40^{\circ}}\,\)
他は図に与えられた通りの点があります。
問\(\,1\,\)
\(\,\mathrm{∠AFC=115^{\circ}}\,\)のときの\(\,\mathrm{∠ABC}\,\)の大きさを求めます。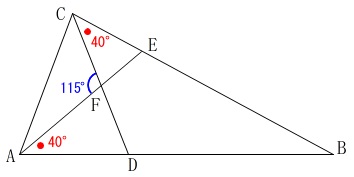
分かる角度を書き込んで行けば普通に求まります。
手っ取り早いのは
\(\,\mathrm{\color{blue}{∠AFC}=\color{red}{∠FCE}+∠FEC}\,\)
なので
\(\begin{eqnarray}
\mathrm{∠FEC}&=&\mathrm{\color{blue}{∠AFC}-\color{red}{∠FCE}}\\
&=&\color{blue}{115^{\circ}}-\color{red}{40^{\circ}}\\
&=&\color{magenta}{75^{\circ}}
\end{eqnarray}\)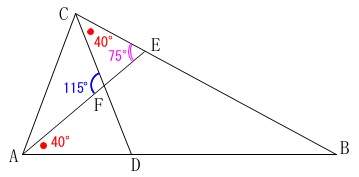
また、
\(\,\mathrm{\color{magenta}{∠AEC}=\color{red}{∠EAB}+∠ABC}\,\)
なので
\(\begin{eqnarray}
\mathrm{∠ABC}&=&\mathrm{\color{magenta}{∠AEC}-\color{red}{∠EAB}}\\
&=&\color{magenta}{75^{\circ}}-\color{red}{40^{\circ}}\\
&=&\underline{ 35^{\circ} }
\end{eqnarray}\)
分かる角度は他にもたくさんあります。
それほど時間に差が出るわけではありません。
やれることはやり尽くしましょう。
それが、問題全体を通じての出題者の意図です。
角度を書き込んで行くと気がつくと思いますが、
四角形\(\,\mathrm{ADEC}\,\)は円に内接しています。
（最初の条件\(\,\mathrm{∠BAE=∠BCD}\,\)の時点で気がつくと早い。）
問\(\,2\,\)
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△EBD}\,\)を証明します。
証明は図の中で完成させておくことです。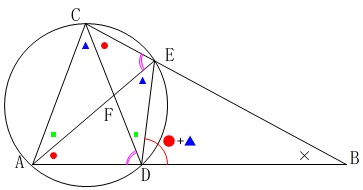
（証明）
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△EBD}\,\)において
\(\,\mathrm{∠ABC=∠EBD\,(共通)} ･･･①\,\)
また、
\(\,\mathrm{\color{red}{∠DAE}=\color{red}{∠DCE}}\,(仮定) ･･･②\)
であることから四角形\(\,\mathrm{ADEC}\,\)は円に内接している。
同一の弧に対する円周角が等しいことから
\(\mathrm{\color{blue}{∠ACD}=\color{blue}{∠AED}} ･･･③\)
さらに、三角形の1つの外角は他の2つの内角の和に等しいので
\(\mathrm{∠EDB=\color{red}{∠DAE}+\color{blue}{∠AED}} ･･･④\)
ここで、②③④より
\(\begin{eqnarray}
\mathrm{∠ACB}&=&\mathrm{\color{red}{∠DCE}+\color{blue}{∠ACD}}\\
&=&\mathrm{\color{red}{∠DAE}+\color{blue}{∠AED}}\\
&=&\mathrm{∠EDB} ･･･⑤
\end{eqnarray}\)
①⑤より
\(\,2\,\)組の角がそれぞれ等しい。
よって、
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△EBD}\,\)
（終わり）
まとめるのに少し苦労するかもしれませんが、
図の中で証明を終わらせて、
それをどういう手順で示したかを書き出せば大丈夫です。
きれいにまとめられなくても論理が飛躍していなければ問題ありません。
（飛んでいると減点されるので日本語で説明を入れても良いですよ。）
裁量問題を指定されている高校の場合は特にですが、
もっと簡単に示して大丈夫でしょう。
\(\color{red}{\fbox{ 定理 }}\)
「円に内接する四角形の1つの外角は、その内角の対角に等しい。」
を使います。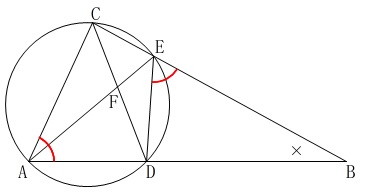
（会員は『円と円周角』のカードで確認しておきましょう。）
四角形\(\,\mathrm{ADEC}\,\)が円に内接していることの後に、
\(\,\mathrm{∠CAB=∠DEB}\,\)
加えておけば共通角と合わせて\(\,2\,\)角相等条件が言えるので証明になります。
定理は一般に成り立ち、一般的に知られている事実です。
標準問題はここまでです。
途中に書いておきましたので出題者の意図を読み取って対策にしてください。
対策は書くことは簡単ですが、
実行するのはあなたしかいないのですよ。
\(\color{black}{\fbox{2}}\)から\(\color{black}{\fbox{5}}\)は裁量問題でもありますので、
次の\(\color{black}{\fbox{ 裁量問題５ }}\)と一緒に見ておいてください。
学校裁量問題の５の解説
方程式、資料、図形と複数の項目があります。
基本的事項に添って問題を読み取りしっかり関係を追っておけば行き届く問題です。
裁量問題受験者向きに解説は簡単にすませます。
問\(\,1\,\)
時間（分）を横\((\,x\,)\)軸、中学校からの道のりを縦\((\,y\,)\)軸にとったグラフがあります。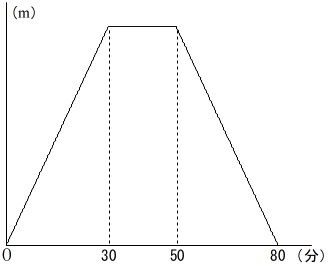
分かっているのは毎分\(\,\mathrm{60\,m}\,\)の速さで移動しているということです。
(1)
中学校から図書館までの道のりを求めます。
毎分\(\,\mathrm{60\,m}\,\)で\(\,30\,\)分移動して図書館まで到達しているので、
\(\hspace{10pt}60\times 30\\
=\underline{ 1800 (\,\mathrm{m}\,)}\)
(2)
往路の速さを復路の\(\,2\,\)倍の速さにして、
図書館での滞在時間を\(\,30\,\)分とし、
全体の所要時間を\(\,80\,\)分のままにするときの往路の速さを求めます。
(1)で図書館までの道のりは\(\,1800\,\)と分かっているので、
往路の速さを\(\,2x\,\)とすると、復路の速さは\(\,x\,\)で、
時間において成り立つ関係式は
\(\hspace{4pt}\displaystyle \frac{1800}{2x}+30+\frac{1800}{x}=80\)
これを解くと復路の速さが\(\,x=54\,\)となります。
よって、往路の速さは\(\,2\,\)倍の
\(\hspace{10pt}2x=108\)
\(\,\mathrm{\underline{ 毎分\,108\,m }}\,\)
（復路の速さが分数になるので往路を\(\,2x\,\)としています。）
移動に使った時間が往復で\(\,50\,\)分なので、
往路で使った時間\(\displaystyle \,50\times\frac{1}{3}\,分\)
復路で使った時間\(\displaystyle \,50\times\frac{2}{3}\,分\)
だから、
往路の速さを\(\,y\,\)、
復路の速さを\(\displaystyle \,\frac{1}{2}\,y\,\)
とすると、道のりの関係で立式すると
\(\displaystyle \frac{50}{3}\times y+\frac{100}{3}\times \frac{y}{2}=3600\)
これから\(\,y=108\,\)と求めることもできます。
または、往路の速さのまま\(\,50\,\)分間歩くと、
中学校と図書館を\(\,1.5\,\)往復することになるので、
往路の速さを\(\,t\,\)として
\(\begin{eqnarray}
50\,t&=&1800\times 2\times 1.5\\
t&=&108
\end{eqnarray}\)
でも良いですけど、時間の方程式が一番分かり易いでしょう。
問\(\,2\,\)
ヒストグラムから平均値を求める問題と、
資料から情報を読み取りヒストグラムを完成させる問題です。
(1)
図１は夏休みのヒストグラムです。
クラス全体で読んだ本の冊数は
\(\begin{array}{|c|c|c|} \hline
一人の冊数 & 人数 & 読んだ本 \\ \hline
0 & 0 & 0 \\ \hline
1 & 2 & 2 \\ \hline
2 & 4 & 8 \\ \hline
3 & 1 & 3 \\ \hline
4 & 2 & 8 \\ \hline
5 & 1 & 5 \\ \hline
6 & 1 & 6 \\ \hline
7 & 3 & 21 \\ \hline
8 & 5 & 40 \\ \hline
9 & 3 & 27 \\ \hline
10 & 3 & 30 \\ \hline
合計 & 25 & 150 \\ \hline
\end{array}\)
クラス\(\,25\,\)人で読んだ本の合計は\(\,150\,\)冊なので、
平均値は
\(\hspace{10pt}\displaystyle \frac{150}{25}=\underline{ 6 (冊) }\)
(2)
冬休みに読んだ本の冊数について、
（資料）からヒストグラムを完成させます。
（資料）を読み取りましょう。
上から①②③④としておきます。
①範囲は夏休みと変わらなかったので、
範囲は\(\,9\,\)冊だから
最小値は\(\,1\,\)冊、最大値は\(\,10\,\)冊
\(\,0\,\)冊だった人は\(\,0\,\)人のまま。
②平均値は変わらなかったことから
\(\,25\,\)人で読んだ総数は\(\,150\,\)冊。
③中央値は冬休みは\(\,8\,\)冊。
（確かに夏休みは\(\,7\,\)冊。）
データを小さい順に並べたときの\(\,13\,\)人目の読んだ冊数は\(\,8\,\)冊。
④\(\,0\,\)冊と\(\,6冊\,\)の度数は\(\,0\,\)。
③から\(\underline{ 7\,冊の度数は\,\color{red}{1} }\)でなければ中央値が\(\,8\,\)冊にならない。
全体で\(\,25\,\)人と分かっているから\(\,8\,\)冊と\(\,9\,\)冊読んだ人の和は\(\,9\,\)人。
\(\,8\,\)冊を\(\,\color{blue}{x}\,\)人とすると\(\,9\,\)冊は\(\,(\color{magenta}{9-x})\,\)人になるので、
累積度数分布表は次のようになります。
※
累積度数は小さい方からその階級までの度数合計です。
\(\begin{array}{|c|c|c|c|} \hline
一人の冊数 & 度数 & 累積度数 & 読んだ冊数 \\ \hline
0 & 0 & 0 & 0 \\ \hline
1 & 4 & 4 & 4 \\ \hline
2 & 3 & 7 & 6 \\ \hline
3 & 1 & 8 & 3 \\ \hline
4 & 1 & 9 & 4 \\ \hline
5 & 2 & 11 & 10 \\ \hline
6 & 0 & 11 & 0 \\ \hline
7 & \color{red}{1} & 12 & 7\\ \hline
8 & \color{blue}{x} & 12+x & 8x\\ \hline
9 & \color{magenta}{9-x} & 21 & 9(9-x)\\ \hline
10 & 4 & 25 & 40 \\ \hline
合計 & 1 & 25 & 150 \\ \hline
\end{array}\)
冊数合計で方程式を立てて\(\,x\,\)（\(\,8\,\)冊の度数）を求めると
\(\hspace{10pt}x=\underline{ 5 }\)
よって、ヒストグラムは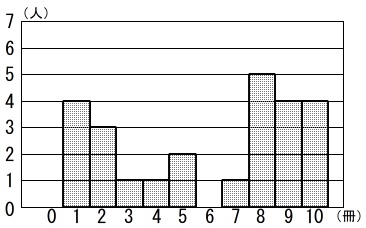
\(\,7\,\)冊の度数が\(\,1\,\)と分かった後、
残りの\(\,9\,\)人を\(\,8\,\)冊と\(\,9\,\)冊に分けて、
\(\,8\,\)冊と\(\,9\,\)冊の読んだ合計が\(\,76\,\)冊になるように調べても良いです。
つまり、
\(\begin{cases}
\hspace{7pt} x+y=9\\
\hspace{7pt} 8x+9y=76
\end{cases}\)
となる\(\,x,y\,\)を求めるということです。
人数なので整数で求まりますが、
中央値が\(\,8\,\)なので\(\,x\,\)は\(\,0\,\)ではありません。
問\(\,3\,\)
線分の長さと回転体の体積を求めます。
条件
\(\,\mathrm{AB=8}\,\)を直径とする半円
\(\,\mathrm{∠ABC=30^{\circ}}\,\)
\(\,\mathrm{D}\,\)は\(\,\mathrm{AB}\,\)の中点
半円なので線分\(\,\mathrm{AB}\,\)が直径になりますが、問題に書いてくれています。
さらにいうなら、点\(\,\mathrm{D}\,\)は円の中心です。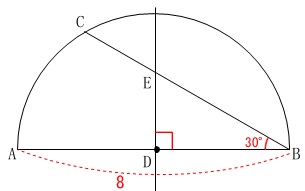
(1)
線分\(\,\mathrm{DE}\,\)の長さを求めます。
\(\,\mathrm{△EBD}\,\)は三角定規で\(\,\mathrm{DB}\,\)は半径の\(\,4\,\)なので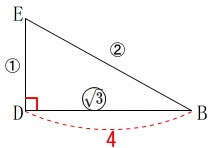
\(\begin{eqnarray}\displaystyle \displaystyle
1:\sqrt{3}&=&\mathrm{DE:DB}\\
1:\sqrt{3}&=&\mathrm{DE}:4\\
\sqrt{3}\,\mathrm{DE}&=&4\\
\mathrm{DE}&=&\frac{4}{\sqrt{3}}\\
&=&\underline{ \frac{4\sqrt{3}}{3} (\,\mathrm{cm}\,)}
\end{eqnarray}\)
長さはすべて分かるので
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△EBD}\,\)
を利用しても良いです。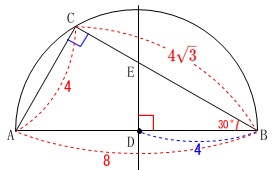
\(\begin{eqnarray}\displaystyle
\mathrm{AC:ED}&=&\mathrm{BC:BD}\\
4:\mathrm{ED}&=&4\sqrt{3}:4\\
4\sqrt{3}\,\mathrm{ED}&=&4\times 4\\
\mathrm{ED}&=&\frac{4\times 4}{4\sqrt{3}}\\
&=&\frac{4\sqrt{3}}{3}
\end{eqnarray}\)
相似に目が行きがちになるので、
この後\(\,\mathrm{△EDB}\,\)だけでも良かったときがつくのではないでしょうか。
時間に余裕があれば、（あまりないだろうけど）
出せる長さはすべて出しておくと最後まで一気に終わりますよ。
(2)
回転体の体積です。
立体を考えるので、見取り図を書きます。
軸は\(\,\mathrm{AB}\,\)なので縦の回転ですが、
\(\,\mathrm{AB}\,\)を立てて横の回転に変えても体積は同じです。
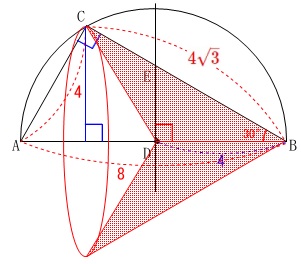円錐から円錐をくり抜いた簡単な体積問題です。
底面が\(\,\mathrm{C}\,\)から\(\,\mathrm{AB}\,\)に下ろした垂線の長さを半径とする円で、
高さを\(\,\mathrm{BD}\,\)とする円錐の体積と同じです。
\(\,\mathrm{△ADC}\,\)は正三角形なので、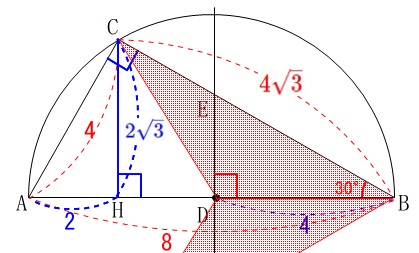
底面の半径は\(\,\color{blue}{2\sqrt{3}}\,\)となります。
よって、求める体積\(\,V\,\)は
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi\times (\,\mathrm{CH}\,)^2\times \mathrm{BD}\\
&=&\frac{1}{3}\times \pi \times (2\sqrt{3})^2\times 4\\
&=&\underline{ 16\,\pi (\,\mathrm{cm^3}\,) }
\end{eqnarray}\)
高さを\(\,\mathrm{BD}\,\)として円錐の体積を出しましたが、
くり抜いた体積で計算しても同じです。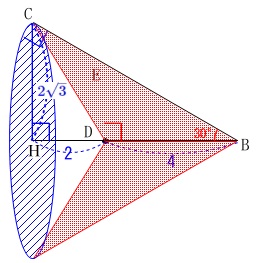
\(\begin{eqnarray}\displaystyle
V&=&\mathrm{\frac{1}{3}\times \pi \times (CH)^2 \times BH}\\
& &\hspace{10pt}-\frac{1}{3}\times \pi \times (\mathrm{CH})^2\times \mathrm{DH}\\
&=&\frac{1}{3}\times \pi \times (\mathrm{CH})^2\times (\mathrm{BH-DH})\\
&=&\frac{1}{3}\times \pi \times (\mathrm{CH})^2\times \mathrm{BD}
\end{eqnarray}\)
具体的に計算した方が分かり易いかもしれませんので、
数値を入れて計算しても良いですよ。
\(\begin{eqnarray}\displaystyle
V&=&\mathrm{\frac{1}{3}\times \pi \times (2\sqrt{3})^2 \times 6}\\
& &\hspace{10pt}-\frac{1}{3}\times \pi \times (2\sqrt{3})^2\times 2\\
&=&24\,\pi-8\,\pi\\
&=&\underline{ 16\,\pi (\,\mathrm{cm^3}\,) }
\end{eqnarray}\)
\(\,\mathrm{2020}\,\)年度北海道公立高校入試の数学は以上です。
裁量問題としては\(\color{black}{\fbox{5}}\)は物足りなく感じたかもしれません。
正直、例年に比べかなり物足りないまま終わりました。
それでも差がつくという原因は、
知識の差でも、計算力でもありません。
もう一度全体を通じて「自分で」答えを導いてみてください。
そうすれば少しは見えてきます。
北海道では毎年、「嫌らしい」と思える問題はありません。
応用問題はありますが受験生の力を測る良い問題構成で出題されていますよ。
※
\(\,\mathrm{2021}\,\)年度は最初にお伝えしたように、
除外される項目がいくつかあります。
応用の広い項目が除外されることで問題の構成が少し（かなり？）変わりますが、
\(\,\mathrm{2020}\,\)年度以上に求められることがはっきりするでしょう。
基本は大切に、何度も復習しておきましょう。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
