大阪府公立高校入試2020年(令和2年)数学Ｃ問題第3問の解説

2020年(令和2年)に大阪府で行われた公立高校入試数学Ｃ問題第３問の解説です。
第３問は立体問題で、面積、角度、線分を求める問題などが５つあります。
線分の長さを聞かれてはいますが体積が必要になったり、総合的な力が試されていますので十分な対策を要します。

大阪府公立高校入試2020年(令和2年)数学Ｃ問題

２０２０年度の問題です。

⇒　２０２０年大阪府立高校入試の数学Ｃ問題

問題はシンプルですが、内容は十分なボリュームを持っています。
\(\,\large{2,3}\,\)で配点されているのは半分以上、
高得点を確保しないと合格は難しいでしょうからさすがに厳しい入学試験問題です。

十分な基礎も欠かせませんが、
合格を手に入れるためには策も必要ですね。

大阪府公立高校入試2020年(令和2年)数学Ｃ問題の解説

Ｃ問題を受験する人向けの解説なので簡単に済ませますので、
不明な点がある場合は基礎力の底上げをしてください。
（ミスが良くあるので気がついた場合はご指摘ください。笑）

問題の条件の整理

全体を通じて言える条件があります。
これは忘れないようにしましょう。

条件
　\(\,\mathrm{ABCD}\,\)は\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)の台形
　\(\,\mathrm{AD=4}\,\)
　\(\,\mathrm{BC=8}\,\)
　\(\,\mathrm{AB=DC=5}\,\)
　四角形\(\,\mathrm{EFGH}\,\)≡四角形\(\,\mathrm{ABCD}\,\)
　\(\,\mathrm{FBCG}\,\)は\(\,1\,\)辺\(\,8\,\)の正方形
　\(\,\mathrm{EFBA,EADH,HGCD}\,\)は長方形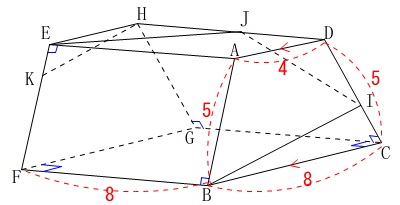
　

(1)距離と面積と角度と線分の長さ

全体に通じる条件に\(\,(1)\,\)で加わる条件があります。

　\(\,\mathrm{DI=3}\,\)
　\(\,\mathrm{J}\,\)は\(\,\mathrm{EJ+JI}\,\)が最小となる点
　\(\,\mathrm{KH}\,\)∥\(\,\mathrm{BI}\,\)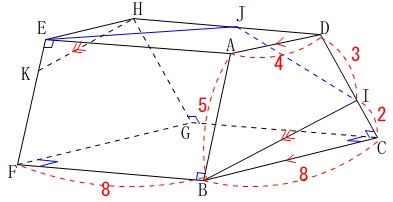

①三角形の面積

\(\,①\,\)\(\,\mathrm{△EJH}\,\)の面積を求めます。

長方形の一部なので\(\,\mathrm{J}\,\)の位置さえつかめれば簡単です。

\(\,\mathrm{J}\,\)は\(\,\mathrm{EJ+JI}\,\)が最小となる点なので、
展開図で見たとき直線になります。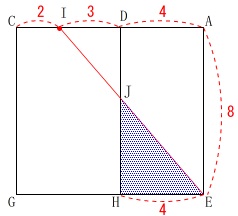高さとなる\(\,\mathrm{HJ}\,\)が分かれば面積が出ます。

　\(\,\mathrm{△JHE}\,\)∽\(\,\mathrm{△JDI}\,\)
　相似比\(\,\mathrm{HE:DI=4:3}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{HJ}&=&\frac{4}{3+4}\times \mathrm{DH}\\
&=&\frac{4}{7}\times 8\\
&=&\color{blue}{\frac{32}{7}}
\end{eqnarray}\)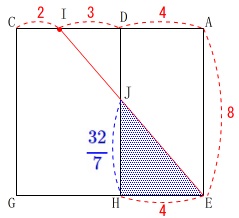よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△EJH}&=&\frac{1}{2}\times \mathrm{\color{red}{HE}}\times \mathrm{\color{blue}{HJ}}\\
&=&\frac{1}{2}\times \color{red}{4}\times \color{blue}{\frac{32}{7}}\\
&=&\underline{　\frac{64}{7}　}　(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

②文字で角度を表す

\(\,②\,\)\(\,\mathrm{∠BIC}\,\)の大きさを文字で表します。

　\(\,\mathrm{∠IBC}=\color{blue}{a}^{\circ}\,,\,\mathrm{∠EKH}=\color{red}{b}^{\circ}\,\)
（以後「度\(\,\mathrm{(^\circ)}\,\)」を省略します。）
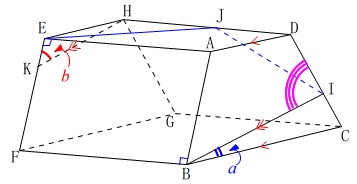遠い！
ということで面を1つにしましょう。

面\(\,\mathrm{ABCD}\,\)側から見ると\(\,\mathrm{HK}\,\)∥\(\,\mathrm{IB}\,\)なので
　\(\,\mathrm{∠ABI=∠EKH}=\color{red}{b}\,\)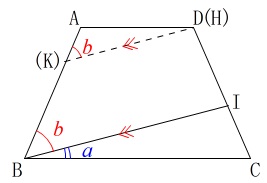四角形\(\,\mathrm{ABCD}\,\)は等脚台形なので
　\(\,\mathrm{∠ABC=∠DCB}=\color{blue}{a}+\color{red}{b}\,\)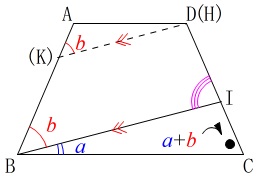よって、
　\(\begin{eqnarray}
\mathrm{∠BID}&=&\mathrm{∠IBC+∠BCI}\\
&=&\color{blue}{a}+(\color{blue}{a}+\color{red}{b})\\
&=&\underline{　2a+b　}　(\,度\,)
\end{eqnarray}\)

③線分の長さ

\(\,③\,\)線分\(\,\mathrm{KF}\,\)の長さを求めます。

\(\,②\,\)で使った透過させた面\(\,\mathrm{ABCD}\,\)を利用しましょう。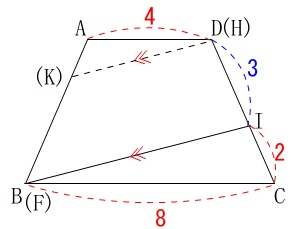
（問題用紙にスペースを作ってくれているので）
相似な三角形ができるように平行線を延長させると
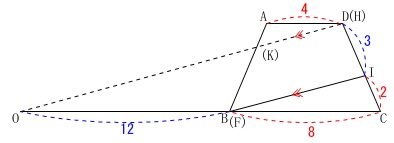　\(\,\mathrm{△A(K)D}\,\)∽\(\,\mathrm{△B(K)O}\,\)
で相似比は
　\(\,\mathrm{AD:BO=\color{red}{4}:\color{blue}{12}=\color{magenta}{1}:\color{magenta}{3}}\,\)
なので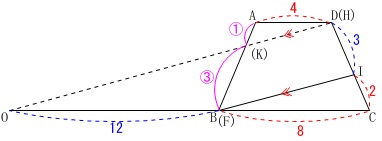
　\(\begin{eqnarray}\displaystyle
\mathrm{KF}&=&\frac{\color{magenta}{3}}{\color{magenta}{1+3}}\times \mathrm{AB}\\
&=&\frac{3}{4}\times 5\\
&=&\underline{　\frac{15}{4}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

(2)立体の対角線の長さと立体の高さ

線分の長さを求める問題が\(\,2\,\)問あります。
どちらも直接は求めることができないのでちょっとした作業は必要ですが、
立体自体が分かり易い形なので答えまでは早いです。

条件は最初の条件に
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DL}\,\)
　\(\,\mathrm{A}\,\)から平面\(\,\mathrm{DFL}\,\)に引いた垂線と平面\(\,\mathrm{DFL}\,\)との交点を\(\,\mathrm{M}\,\)
が加えられます。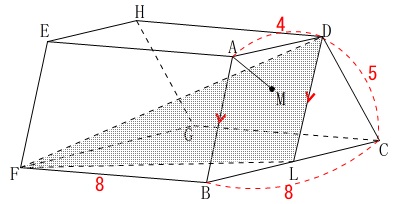　この後立体でポイントとなることが問われます。

①立体の対角線の長さ

\(\,①\,\)線分\(\,\mathrm{DF}\,\)の長さを求めます。

立体では面を抜き出して考えた方が分かり易いので、
求める長さを含む面を抜き出しましょう。

線分\(\,\mathrm{FD}\,\)を含む面は\(\,\mathrm{△FDL}\,\)ですが、
問題にも書いてくれていますが\(\,\mathrm{△FDL}\,\)は直角三角形ではありません。

\(\,2\,\)辺は分かりますが問題の\(\,\mathrm{FD}\,\)にはちょっと遠回りになりそうなのでやめておきましょう。

\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろします。
交点を\(\,\mathrm{N}\,\)とすると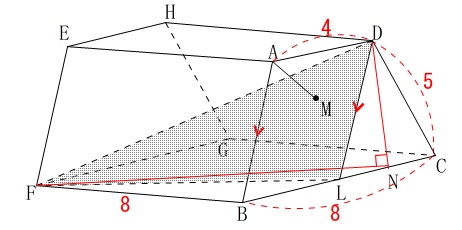\(\,\mathrm{△FND}\,\)は直角三角形になるので三平方の定理が使えます。

辺\(\,\mathrm{DN}\,\)は\(\,\mathrm{△DLC}\,\)において（抜き出して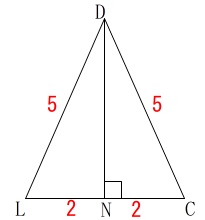）、三平方の定理から
　\(\begin{eqnarray}
\mathrm{DN^2}&=&\mathrm{DL^2-LN^2}\\
&=&5^2-2^2\\
&=&21\\
\mathrm{DN}&=&\color{blue}{\sqrt{21}}　(\,\mathrm{DN}\,＞\,0\,)
\end{eqnarray}\)

また、辺\(\,\mathrm{FN}\,\)は\(\,\mathrm{△FNB}\,\)において（抜き出して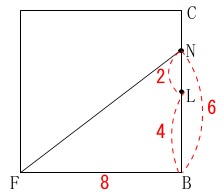）三平方の定理から
　\(\begin{eqnarray}
\mathrm{FN^2}&=&\mathrm{FB^2+BN^2}\\
&=&8^2+6^2\\
&=&100\\
\mathrm{FN}&=&\color{magenta}{10}　(\,\mathrm{FN}\,＞\,0\,)
\end{eqnarray}\)

よって、\(\,\mathrm{△FDN}\,\)において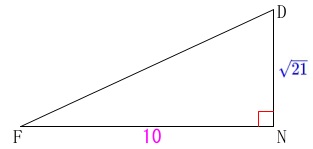もう一度三平方の定理を用いて
　\(\begin{eqnarray}
\mathrm{DF^2}&=&\mathrm{FN^2+DN^2}\\
&=&\color{magenta}{10}^2+(\color{blue}{\sqrt{21}})^2\\
&=&121\\
\mathrm{DF}&=&\underline{　11　}　(\,\mathrm{DF}\,＞\,0\,)
\end{eqnarray}\)

基本通り平面を抜き出す作業を繰り返せば難しいことはありません。

ただ、もう少し早い方法はあります。

奥にある\(\,\mathrm{△DNC}\,\)を底面とする三角柱を切り取り、
ひっくり返して手前にひっつけたとすると直方体なので

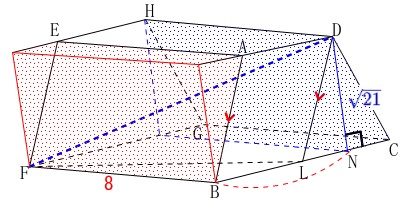
　\(\begin{eqnarray}
\mathrm{FD^2}&=&\mathrm{FB^2+BN^2+DN^2}\\
&=&8^2+6^2+(\sqrt{21})^2\\
&=&121
\end{eqnarray}\)
とすることもできますが、大して変わりません。

直方体の対角線は公式化されていますが、
平面を抜き出すという基本作業の方が応用範囲はだんぜん広いです。
もちろん、時間短縮には公式は使った方が良いですが、
公式が使える形に変形できることをいつも思いつくとは限りません。

②高さとなる線分の長さ

\(\,②\,\)\(\,\mathrm{A}\,\)から平面\(\,\mathrm{DLF}\,\)に下ろした垂線\(\,\mathrm{AM}\,\)の長さを求めます。
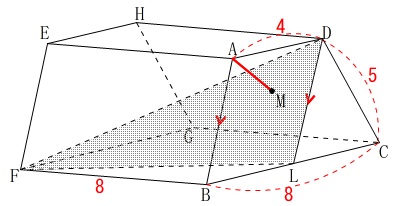この問題が一番取り組みやすかったのではないでしょうか。

一見、難しそうに見えますが、垂線は高さと同じです。

立体を転がして同じ体積どうしを見比べる問題はよく出るので、
方針はすぐに立った人が多かったでしょう。

ただし、作業量はやはり多いです。
迷っているヒマはありません。

線分\(\,\mathrm{AM}\,\)が高さとなる立体は底面を\(\,\mathrm{△FDL}\,\)とする三角錐です。

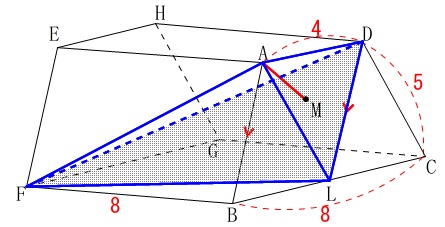
一方で、この立体は
　底面を\(\,\mathrm{△ADL}\,\)
　高さを\(\,\mathrm{FB}\,\)
とする三角錐でもあります。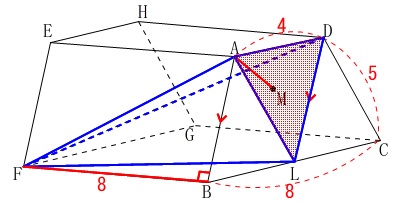体積はこちらの方が先に出せますが、
高さがずれているのでわかりにづらいときは底面を下にして転がしてみると良いです。
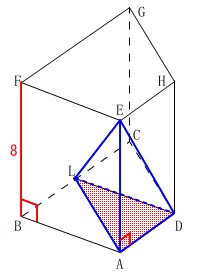　\(\,\mathrm{EA=FB}\,\)
が高さとなるので、
　\(\,\mathrm{F-ADL}\,\)と\(\,\mathrm{E-ADL}\,\)は同じ体積
となります。

ここで底面となる\(\,\mathrm{△ADL}\,\)の面積は\(\,\mathrm{△DLC}\,\)と同じで、
この三角形の高さは①で求めた通りで
　\(\,\mathrm{DN=\sqrt{21}}\,\)
なので\(\,\mathrm{△ADL}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ADL}&=&\mathrm{△ADL}\\
&=&\frac{1}{2}\times 4\times \sqrt{21}\\
&=&2\sqrt{21}
\end{eqnarray}\)

これから三角錐\(\,\mathrm{F-ADL}\,\)の体積\(\,V\,\)は
　高さ\(\,\mathrm{FB=EA=8}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{V}&=&\frac{1}{3}\times \mathrm{△ADL}\times \mathrm{FB}\\
&=&\frac{1}{3}\times 2\sqrt{21}\times 8\\
&=&\color{blue}{\frac{16\sqrt{21}}{3}}
\end{eqnarray}\)

今度は底面を\(\,\mathrm{△DFL}\,\)とみます。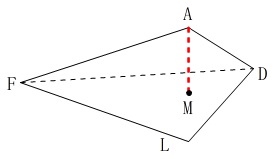底面となる\(\,\mathrm{△DFL}\,\)の面積を求めるために抜き出します。

\(\,\mathrm{△FBL}\,\)から
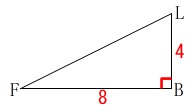　\(\begin{eqnarray}
\mathrm{FL^2}&=&\mathrm{FB^2+BL^2}\\
&=&4^2+8^2\\
&=&\color{red}{80}
\end{eqnarray}\)

これから\(\,\mathrm{FL=4\sqrt{5}}\,\)、
（となりますが平方のまま使うので必要ありません。）
なので\(\,\mathrm{△DFL}\,\)は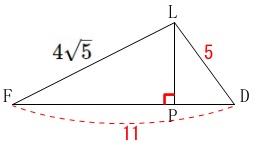\(\,\mathrm{L}\,\)から\(\,\mathrm{FD}\,\)に垂線を下ろし\(\,\mathrm{FD}\,\)との交点を\(\,\mathrm{P}\,\)とすると、
線分\(\,\mathrm{LP}\,\)が高さとなります。

線分\(\,\mathrm{PD}=x\,\)とおくと\(\,\mathrm{FP}=11-x\,\)で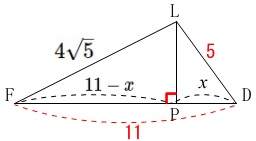　\(\begin{eqnarray}
\mathrm{LP^2}&=&\mathrm{LD^2-PD^2}\\
&=&\mathrm{FL^2-FP^2}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}
5^2-x^2&=&(4\sqrt{5})^2-(11-x)^2\\
25-x^2&=&\color{red}{80}-121+22x-x^2\\
66x&=&22x\\
x&=&3
\end{eqnarray}\)

これから\(\,\mathrm{△DFL}\,\)の高さ\(\,\mathrm{LP}\,\)は
　\(\begin{eqnarray}
\mathrm{LP^2}&=&\mathrm{LD^2-PD^2}\\
&=&5^2-3^2\\
&=&16\\
\mathrm{LP}&=&4　(\,＞\,0\,)
\end{eqnarray}\)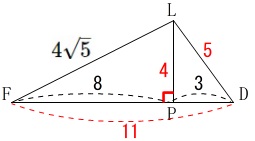
このことから底面\(\,\mathrm{△DFL}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△DFL}&=&\frac{1}{2}\times \mathrm{FD}\times \mathrm{LP}\\
&=&\frac{1}{2}\times 11\times 4\\
&=&22
\end{eqnarray}\)

高さが\(\,\mathrm{AM}\,\)なので三角錐\(\,\mathrm{A-DFL}\,\)の体積\(\,V’\,\)は
　\(\begin{eqnarray}\displaystyle \color{red}{V’}&=&\frac{1}{3}\times\mathrm{ △DFL}\times \mathrm{AM}\\
&=&\color{red}{\frac{1}{3}\times 22\times \mathrm{AM}}\end{eqnarray}\)

三角錐\(\,\mathrm{F-ADL}\,\)と\(\,\mathrm{A-DFL}\,\)は同じ体積なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{V}&=&\color{red}{V’}\\
\color{blue}{\frac{16\sqrt{21}}{3}}&=&\color{red}{\frac{1}{3}\times 22\times \mathrm{AM}}\\
\mathrm{AM}&=&\underline{　\frac{8\sqrt{21}}{11}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

長ったらしい解説になりましたが、
自分で計算を進めるとそれほど時間がかからないことが分かります。
人の計算見て、自分でやった気にならないようにしましょう。

⇒　大阪府公立高校入試2020年(令和2年)数学Ｃ問題第2問の解説

合否を分けるのは\(\,\mathrm{\large{2,3}}\,\)です。
満点を狙うならもっと上の力が必要ですが、
数学で\(\,\mathrm{8}\,\)割程度確保できれば良いのであれば、
基礎知識、ある程度の計算力、そして作業によって拾える問題を確実に結果までだす。

それができれば\(\,\mathrm{C}\,\)問題選択校でも十分合格可能な受験生達でしょう。
この解説をここまで読んでくれた受験生、応援しています！

⇒　大阪府公立高校入試数学の過去問と解答解説

数年分の解説を見て頂ければ分かりますが、
見ているだけで解ける問題は\(\,\mathrm{C}\,\)問題にはほとんどありません。
進学先の高校では、自分で手を動かして解決の糸口を見つける、それが必要だからです。