2020年愛知県公立高校入試A日程の数学問題の解説

2020年(令和2年）に愛知県で行われた公立高校入試A日程の数学問題の解説です。
変に難問が並ぶわけではありませんが、基本知識、計算力、だけでは不足します。
難易度的には例年と変わりないですが、激戦区でもあり時間的にも楽ではありませんね。

2020年愛知県公立高校入試A日程の数学の問題

問題は大問3つです。

⇒　2020年愛知県公立高校入試A日程の数学の問題

\(\,3\,\)問は決して少なくない質と量です。

2020年愛知県公立高校入試A日程の数学の問題の解説

第１問第２問は単独項目ではありませんので、
1つひとつ切り換えて進めて行きましょう。
※
詳しく解説するとものすごく長くなる問題が多いので、
\(\,\mathrm{2}\,\)点を通る直線を求める、
方程式を解く、
といった、自分でやればできる部分は省略しますのでご了承ください。
※※
ミスにお気づきの際はご指摘ください。

第１問

\(\,\large{1}\,\)

\(\,9\,\)問の小問集合になっています。

計算問題も楽な問題ばかりではありませんのでミスには気をつけましょう。

(1)
　\(\hspace{10pt}3-4\times (-2)\\
=3+8\\
=\underline{　11　}\)

足し算引き算より掛け算割り算が先です。

(2)
　\(\hspace{10pt}\displaystyle　\frac{2}{3}\,(2x-3)-\frac{1}{5}\,(3x-10)\\
\displaystyle =\frac{10(2x-3)-3(3x-10)}{15}\\
\displaystyle =\frac{20x-30-9x+30}{15}\\
\displaystyle =\underline{　\frac{11x}{15}　}=\underline{　\frac{11}{15}\,x　}\)

好きに計算して良いですけど、
通分して、分母は一つに分子の計算に集中した方が早いし確実です。
答えはどちらの形でも同じものを表しています。

(3)
　\(\hspace{10pt}(\sqrt{10}+\sqrt{5})(\sqrt{6}-\sqrt{3})\\
=\color{red}{\sqrt{60}}-\sqrt{30}+\sqrt{30}\color{blue}{-\sqrt{15}}\\
=\color{red}{2\sqrt{15}}\color{blue}{-\sqrt{15}}\\
=\underline{　\sqrt{15}　}\)

素直に展開する方法で良いです。
そのまま展開するなら素因数分解を確実にやっておきましょう。

　\(\hspace{10pt}(\sqrt{10}+\sqrt{5})(\sqrt{6}-\sqrt{3})\\
=\color{red}{\sqrt{5}}(\color{blue}{\sqrt{2}+1})\color{red}{\sqrt{3}}(\color{blue}{\sqrt{2}-1})\\
=\color{red}{\sqrt{15}}(\color{blue}{2-1})\\
=\underline{　\sqrt{15}　}\)

因数が見えれば、で良いです。

(4)
２次方程式を解きます。

　\(\begin{eqnarray}
2x^2+5x+3&=&x^2+6x+6\\
x^2-x-3&=&0
\end{eqnarray}\)

因数分解はできないので解の公式を利用します。

2次方程式の解の公式は
　\(ax^2+bx+c=0\)
において
　\(\hspace{10pt}\displaystyle \color{red}{x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}\)
です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{1\pm \sqrt{1+12}}{2}\\
&=&\underline{　\frac{1\pm \sqrt{13}}{2}　}
\end{eqnarray}\)

方程式を解くことと、解を求めることは同じです。

(5)
展開ではありません。
因数分解です。

　\(\hspace{10pt}5x(x-2)-(2x+3)(2x-3)\\
=5x^2-10x-(4x^2-9)\\
=5x^2-10x-4x^2+9\\
=x^2-10x+9\\
=\underline{　(x-1)(x-9)　}\)

展開で終わらないように注意しましょう。

(6)
過不足の方程式です。

何を等号で結ぶかです。
変わらないのが人数と材料費なので材料費で方程式を立てます。

\(\,300\,\)円ずつ集めると\(\,2600\,\)円不足するということは、
材料費は集めた金額より\(\,2600\,\)円大きい。

\(\,400\,\)円ずつ集めると\(\,1200\,\)円余るということは、
材料費は集めた金額より\(\,1200\,\)円小さい。

人数を\(\,x\,\)とすると方程式は
　\(\hspace{10pt}300x+2600=400x-1200\)

これを解いて、
　\(\begin{eqnarray}
300x+2600&=&400x-1200\\
-100x&=&-3800\\
x&=&\underline{　38　(人)}
\end{eqnarray}\)

人数なので\(\,x\,\)が整数で無ければ計算ミスしています。

(7)
ボールが転がるとか関係ありません。
関数の\(\,2\,\)点間の変化の割合を求めます。

関数\(\,y=3x^2\,\)において
　\(\,x=2\,\)のとき\(\,y=12\,\)
　\(\,x=4\,\)のとき\(\,y=48\,\)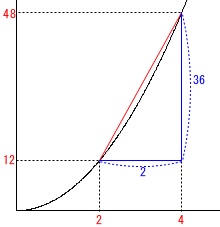なので
　「\(\,2\,\)秒間で\(\,\mathrm{36\,m}\,\)移動した。」
ということになります。

　\(\hspace{4pt}\displaystyle \frac{48-12}{4-2}=\frac{36}{2}=18\)

これが平均の速さになります。

答え　\(\,\underline{　\mathrm{毎秒　18　m}　}\,\)

(8)
\(\,20\,\)通りの組み合わせの確立です。
樹形図を書き出せば終わります。

　\(\,\mathrm{A}\,\)から取り出す数字が\(\,5\,\)通り
　\(\,\mathrm{B}\,\)から取り出す数字が\(\,4\,\)通り
あるので取り出し方は全部で\(\,20\,\)通りあります。

2つの数の積が奇数になるのは両方奇数のときで、
\(\,\mathrm{A,B}\,\)から取り出す\(\,2\,\)数両方が奇数の場合です。

両方が奇数の取り出し方は、
　\(\,\mathrm{A}\,\)から\(\,1,3,5\,\)の\(\,3\,\)通り
　\(\,\mathrm{B}\,\)から\(\,1,3,5\,\)の\(\,3\,\)通り
あるので\(\,9\,\)通り。

よって、\(\,2\,\)数の積が奇数になる確率は
　\(\hspace{10pt}\displaystyle \underline{　\frac{9}{20}　}\)

(9)
良くある円と接線の問題ですが
\(\,\mathrm{2}\,\)円と共通接線があれば接点と中心を結びます。

中心\(\,\mathrm{Q}\,\)を通り、\(\,\mathrm{AB}\,\)に平行な線を引くと、
線分\(\,\mathrm{AB}\,\)と等しい線分ができます。
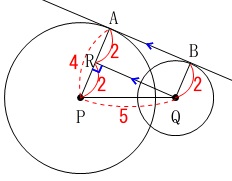平行線と線分\(\,\mathrm{AP}\,\)との交点を\(\,\mathrm{R}\,\)とすると、
　\(\hspace{10pt}\mathrm{\color{red}{AB}=\color{red}{QR}}\)
\(\,\mathrm{△PQR}\,\)において三平方の定理を用いて
　\(\begin{eqnarray}
\mathrm{PQ^2}&=&\mathrm{PR^2+QR^2}\\
5^2&=&2^2+\mathrm{QR^2}\\
\mathrm{QR^2}&=&5^2-2^2\\
&=&25-4\\
&=&21\\
\mathrm{\color{red}{QR}}&=&\sqrt{21}　(\,＞\,0\,)
\end{eqnarray}\)

よって、
　\(\hspace{10pt}\mathrm{\color{red}{AB}}=\underline{　\sqrt{21}　(\,\mathrm{cm}\,)}\)

ポイントは1つ。
図に分かることを書き込む、それだけです。

第２問

\(\,\large{2}\,\)

小問が\(\,4\,\)問あります。

(1)
3つの数の和が等しくなるように図にあるア、イに入る数字を求めます。
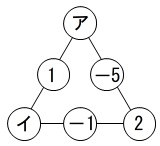連立方程式でも良いですが、
ア、イに何が入っても成り立つ関係からすぐに求まります。

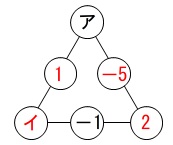
アが何であっても、
　\(\,(\color{red}{イ})+(\color{red}{1})=(\color{red}{-5})+(\color{red}{2})\,\)
なので、
　\(\,イ　\underline{　-4　}\,\)

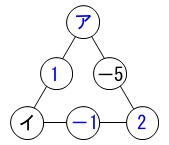
イが何であっても、
　\(\,(\color{blue}{ア})+(\color{blue}{1})=(\color{blue}{-1})+(\color{blue}{2})\,\)
なので、
　\(\,ア　\underline{　0　}\,\)

連立方程式を利用する場合は、
アを\(\,x\,\)、イを\(\,y\,\)として、
　\(\hspace{4pt}x+1+y=x-3=y+1\)
を解くことになります。

(2)
資料の度数分布表から平均値と中央値を読み取ります。

問題が\(\,3\,\)問しか無いので正誤の違いは\(\,8\,\)通りしかありません。
第１問は正解すれば１点、第２門と第３問は正解すれば２点です。

　\(\begin{array}{|c|c|c|c|} \hline
第１問 & 第２問 & 第３問 & 得点 \\ \hline
○ & ○ & ○ & 5 \\ \hline
○ & ○ & × & 3 \\ \hline
○ & × & ○ & 3 \\ \hline
○ & × & × & 1 \\ \hline
× & ○ & ○ & 4 \\ \hline
× & ○ & × & 2 \\ \hline
× & × & ○ & 2 \\ \hline
× & × & × & 0 \\ \hline
\end{array}\)

これを読み取れていれば大丈夫です。

問題にある度数分布表から平均値は、
　\(\hspace{10pt}\displaystyle \frac{45+36+30+12+5+0}{40}\\
\displaystyle =\frac{128}{40}\\
=3.2\)

　\(\hspace{10pt}a　\underline{　3.2　}　点\)

平均値は総得点を度数で割ったものです。

中央値は小さい（または大きい）得点順に並べたときに、
\(\,20\,\)番目と\(\,21\,\)番目にいる人の平均値です。
ただし、ここでは同じ得点なので平均を出す必要はありません。

\(\,5\,\)点、\(\,4\,\)点までで\(\,18\,\)人いますので、
\(\,20\,\)番目\(\,21\,\)番目の人は\(\,3\,\)点の\(\,10\,\)人の中にいます。

　\(\hspace{10pt}b　\underline{　3　}　点\)

第１問を正解した人の得点は奇数得点になるので、
（第２問、第３問は\(\,2\,\)点だから）
点数が\(\,1\,\)点、\(\,3\,\)点、\(\,5\,\)点の人は第１問を正解しています。

　\(\hspace{10pt}9+10+5\\
=24\)

　\(\hspace{10pt}c　\underline{　24　}　人\)

もう一つは正解した問題数の平均値です。

もう一度得点パターンを見てください。
　\(\begin{array}{|c|c|c|c|c|} \hline
第１問 & 第２問 & 第３問 & 得点 \\ \hline
○ & ○ & ○ & 5 \\ \hline
○ & ○ & × & 3 \\ \hline
○ & × & ○ & 3 \\ \hline
○ & × & × & 1 \\ \hline
× & ○ & ○ & 4 \\ \hline
× & ○ & × & 2 \\ \hline
× & × & ○ & 2 \\ \hline
× & × & × & 0 \\ \hline
\end{array}\)

問題の度数分布表から
\(\,5\,\)点の人は\(\,3\,\)問正解の\(\,9\,\)人
\(\,4\,\)点、\(\,3\,\)点の人は\(\,2\,\)問正解の\(\,19\,\)人
\(\,2\,\)点、\(\,1\,\)点の人は\(\,1\,\)問正解の\(\,11\,\)人
\(\,0\,\)点の人は正解なしの\(\,1\,\)人
となっているので正解した問題数の平均値は
　\(\hspace{10pt}\displaystyle \frac{27+38+11+0}{40}\\
\displaystyle =\frac{76}{40}\\
=1.9\)

　\(\hspace{10pt}d　\underline{　1.9　}　問題\)

(3)
反比例のグラフ上の\(\,2\,\)点と、
　原点とで作る三角形と、
　\(\,x\,\)軸上の点で作る三角形の、
面積が等しくなるときの座標を求めます。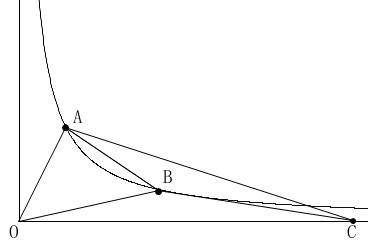\(\,\mathrm{△AOB=△ABC}\,\)となるときの点\(\,\mathrm{C}\,\)の座標です。

方法はいくつか考えられますが、
等積移動を利用した方法で示しておきます。

底辺を同じとした三角形は、
高さが等しければ面積は等しくなります。

この場合は底辺を\(\,\mathrm{AB}\,\)と見ると、
\(\,\mathrm{AB}\,\)と平行な直線上を移動すれば面積は変わらないのですが、
原点\(\,\mathrm{O}\,\)は\(\,\mathrm{C}\,\)と反対側にあるので切片で考えます。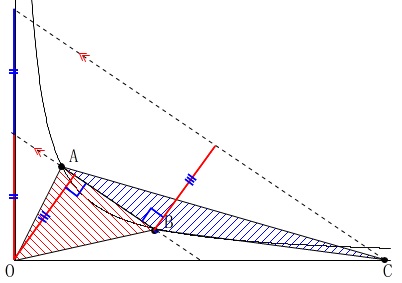
\(\,2\,\)点\(\,\mathrm{A,B}\,\)を通る直線は
　\(\,\mathrm{A\,(\,1\,,\,2\,)}\,\)
　\(\,\displaystyle \mathrm{B}\,\left(\,3\,,\,\frac{2}{3}\right)\,\)
なので、
　\(\hspace{10pt}\displaystyle y=-\frac{2}{3}\,x+\frac{8}{3}\)

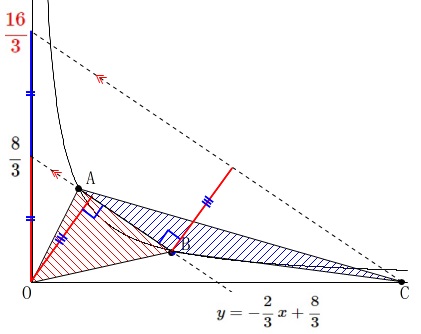
傾きは\(\,\mathrm{AB}\,\)と同じで切片が
　\(\displaystyle \color{red}{\frac{16}{3}}\)
となれば\(\,\mathrm{△AOB=△ABC}\,\)になるので、
　\(\hspace{10pt}\displaystyle y=-\frac{8}{3}\,x+\color{red}{\frac{16}{3}}\)
の\(\,x\,\)軸との交点の座標が求める点\(\,\mathrm{C}\,\)の座標です。

\(\,x\,\)軸は\(\,y=0\,\)なので
　\(\begin{eqnarray}\displaystyle
-\frac{2}{3}\,x+\frac{16}{3}&=&0\\
x&=&8
\end{eqnarray}\)
から
　\(\hspace{4pt}\mathrm{C}\,\underline{　(\,8\,,\,0\,)　}\)

点\(\,\mathrm{C}\,\)を
　\(\hspace{4pt}\mathrm{C}\,(\,t\,,\,0\,)\)
とおいて三点で作る面積の計算をしてもすぐに求まります。
会員の方はやっておいてください。
（一般には通じないし、説明が長くなるのでここではやりません。）

(4)
これも良くある問題ですが、
条件を読み取り整理しておきましょう。

　\(\,\mathrm{A-C-B}\,\)間\(\,\mathrm{12\,km}\,\)の道のりを移動する。
　\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)までは\(\,\mathrm{8\,km}\,\)
\(\,\mathrm{S}\,\)さん：
　\(\,\mathrm{A}\,\)から毎時\(\,\mathrm{12km}\,\)で\(\,\mathrm{C}\,\)に移動、
　\(\,5\,\)分休憩後同じ速さで\(\,\mathrm{B}\,\)に移動。
バス：
　\(\,\mathrm{A-B}\,\)間を往復する。
　\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)には時速\(\,\mathrm{48\,km}\,\)
　\(\,\mathrm{B}\,\)から\(\,\mathrm{A}\,\)には時速\(\,\mathrm{36\,km}\,\)
　\(\,\mathrm{A,B}\,\)それぞれに到着後\(\,5\,\)分停車
　出発は\(\,\mathrm{B}\,\)から。
\(\,\mathrm{S}\,\)さんとバスは同時に出発する。

①
\(\,\mathrm{S}\,\)さんの移動をグラフにします。
軸が\(\,\mathrm{\color{red}{分}}\,\)と\(\,\mathrm{km}\,\)なので時速を分速に変えておきます。

時速\(\,\mathrm{12\,km}\,\)は分速に換えると
　\(\hspace{4pt}\displaystyle \frac{12}{60}=\frac{1}{5}　(\mathrm{km/分})\)
となります。

グラフを描くだけなら関数は必要ありません。

\(\,\mathrm{A}\,\)を出発して\(\,\mathrm{8\,km}\,\)離れた\(\,\mathrm{C}\,\)には\(\,40\,\)分後に到着し、
\(\,5\,\)分休憩して、
\(\,\mathrm{C}\,\)を出発して\(\,\mathrm{4\,km}\,\)離れた\(\,\mathrm{B}\,\)に\(\,20\,\)分後に到着します。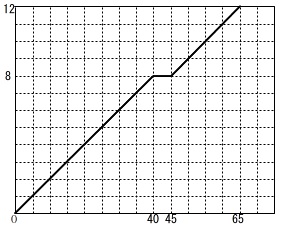
②に進んで良いですが、直線の方程式を出しておきます。

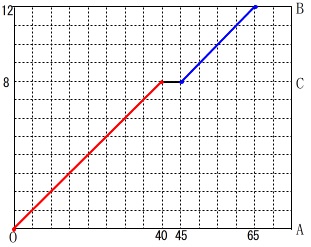
\(\,\mathrm{\color{red}{A-B}}\,\)間：\(\hspace{4pt}\displaystyle y=\frac{1}{5}\,x\)
\(\,\mathrm{\color{blue}{B-C}}\,\)間：\(\hspace{4pt}\displaystyle y=\frac{1}{5}\,x-1\)

交点を求めるときはグラフから読み取るのは正確とは言えません。
関数を連立することで正確に読み取ります。

②
\(\,\mathrm{S}\,\)さんとバスが最後にすれ違うときが、
出発してから何分後かを求めます。

バスの速さは
\(\,\mathrm{A\,\rightarrow \,B}\,\)では
　\(\hspace{4pt}\displaystyle \frac{48}{60}=\frac{4}{5}　(\,\mathrm{km}/分\,)\)
\(\,\mathrm{B\,\rightarrow \,A}\,\)では
　\(\hspace{4pt}\displaystyle \frac{36}{60}=\frac{3}{5}　(\,\mathrm{km}/分\,)\)
これは関数では負の値です。

グラフにバスの移動を書き込んでおきます。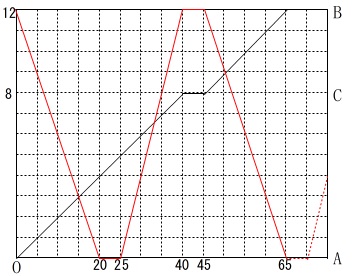グラフが交わるところが同じ位置にいるということです。
見た目では最後にすれ違うのは\(\,50\,\)分後ですが、
少しずれている様にも見えます。（わざとです。笑）

正確に交点を出すには連立します。

\(\,\mathrm{S}\,\)さんが\(\,\mathrm{B}\,\)から\(\,\mathrm{C}\,\)に移動するときの関数は
　\(\hspace{4pt}\displaystyle y=\frac{1}{5}\,x-1\)

バスが\(\,\mathrm{B}\,\)から\(\,\mathrm{A}\,\)に向かう\(\,45\,\)分後からの関数は
　\((\,45\,,\,12\,)\)
　\((\,65\,,\,0\,)\)
を通るので
　\(\hspace{4pt}\displaystyle y=-\frac{3}{5}\,x+39\)

よって、交点の\(\,x\,\)座標が最後にすれ違うときで
　\(\begin{eqnarray}\displaystyle
\frac{1}{5}\,x-1&=&-\frac{3}{5}\,x+39\\
x-5&=&-3x+195\\
4x&=&200\\
x&=&\underline{　50　(分後)}　
\end{eqnarray}\)

合っていました。
定規で直線を引けば交点はきれいに\(\,\mathrm{50}\,\)分後になる軸の取り方をしてくれています。
ただ、交点が読み取れない場合もあるので連立して確実に出すようにしておきましょう。

第３問

\(\,\large{3}\,\)
角度、相似、体積など図形総合問題です。

(1)
\(\,\mathrm{∠DEC}\,\)の大きさを求めます。
与えられた角度は必要だから与えられていることを忘れないでください。

　\(\,\mathrm{∠COA=40^{\circ}}\,\)
　\(\,\mathrm{∠DBE=36^{\circ}}\,\)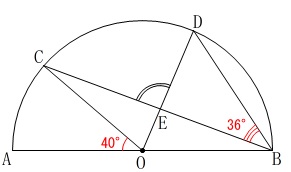中心角と円周角の関係でも良いですし、
半径が等しいことから二等辺三角形の底角でも良いです。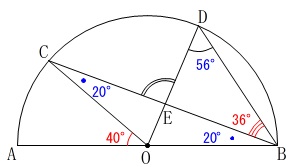\(\,\mathrm{△OBC}\,\)が二等辺三角形であることから
　\(\,\mathrm{∠OBC=∠OCB=\color{blue}{20^{\circ}}}\,\)

\(\,\mathrm{△OBD}\,\)が二等辺三角形であることから
　\(\,\mathrm{∠OBD=∠ODB=\color{blue}{56^{\circ}}}\,\)

よって
　\(\begin{eqnarray}
\mathrm{∠DEC}&=&\mathrm{∠DBE+∠BDE}\\
&=&\color{red}{36^{\circ}}+\color{blue}{56^{\circ}}\\
&=&92^{\circ}
\end{eqnarray}\)

答え　\(\,\underline{　92　度}\,\)

または、
円周角\(\,\mathrm{∠CBD=\color{red}{36^{\circ}}}\,\)から
中心角\(\,\mathrm{∠COD=\color{magenta}{72^{\circ}}}\,\)なので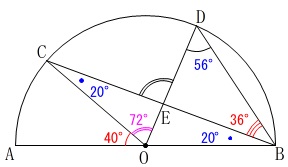
　\(\begin{eqnarray}
\mathrm{∠DEC}&=&\mathrm{∠ECO+∠EOC}\\
&=&\color{blue}{20^{\circ}}+\color{magenta}{72^{\circ}}\\
&=&\underline{　92^{\circ}　}
\end{eqnarray}\)

(2)
線分比と円の面積比を求めます。

長方形は平行四辺形なので平行線と相似を利用しますが、
その前に条件を見ておきます。

　\(\,\mathrm{ABCD}\,\)は長方形
　\(\,\mathrm{EC=2BE}\,\)
　\(\,\mathrm{FC=3DF}\,\)
　\(\,\mathrm{AB=4\,,\,AD=6}\,\)

条件から
　\(\,\mathrm{BE=\color{red}{2}\,,\,EC=\color{red}{4}}\,\)
　\(\,\mathrm{DF=\color{red}{1}\,,\,FC=\color{red}{3}}\,\)
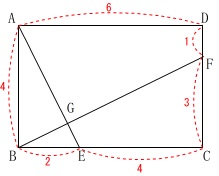これらは比では無く長さです。

①\(\,\mathrm{AG}\,\)と\(\,\mathrm{GE}\,\)の比を求めます。

\(\,\mathrm{ABCD}\,\)は長方形（平行四辺形）なので、
\(\,\mathrm{BF}\,\)の延長と\(\,\mathrm{AD}\,\)の交点を\(\,\mathrm{H}\,\)とすると、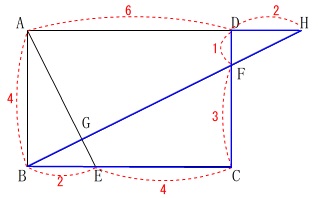
　\(\,\mathrm{△FDH}\,\)∽\(\,\mathrm{△FCB}\,\)
で相似比は
　\(\,\mathrm{FD:FC=1:3}\,\)
なので
　\(\begin{eqnarray}
\mathrm{DH:CB}&=&1:3\\
&=&\color{red}{2}:\color{red}{6}
\end{eqnarray}\)
さらに、
　\(\,\mathrm{△GBE}\,\)∽\(\,\mathrm{△GHA}\,\)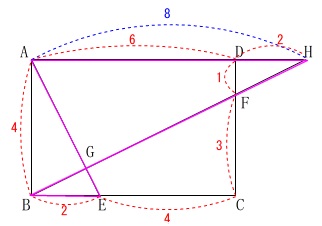相似比は
　\(\,\mathrm{BE:HA=2:8}\,\)
なので
　\(\,\mathrm{AG:EG=4:1}\,\)

答え　\(\,\underline{　4　}　倍\,\)

\(\,\mathrm{DC}\,\)と\(\,\mathrm{AE}\,\)を延長しても良いですよ。
同じ手順で答えが出ます。

②
\(\,3\,\)点\(\,\mathrm{A,F,G}\,\)を通る円と、
\(\,3\,\)点\(\,\mathrm{E,F,G}\,\)を通る円の面積比を求めます。
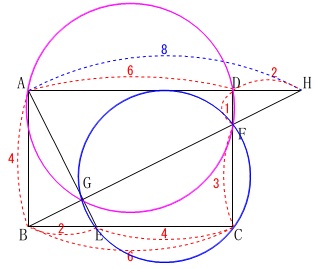「どうやって？」と悩んだ人が多いかもしれませんが、
最初の条件から
　\(\,\mathrm{AE}\,\)　⊥　\(\,\mathrm{GF}\,\)
が分かるので、2つの円は、
　\(\,\mathrm{AF}\,\)と\(\,\mathrm{EF}\,\)が直形の円だと分かります。

円はすべて相似になるので、
直径の比が相似比になることを利用すれば簡単です。

　\(\,\mathrm{AE}\,\)　⊥　\(\,\mathrm{BF}\,\)
であることをちょっと説明します。

相似な図形が多くて見分けにくいですが、
　\(\,\mathrm{△HDF}\,\)∽\(\,\mathrm{△ABE}\,\)
（\(\,2\,\)辺の比とその間の角がそれぞれ等しい。）
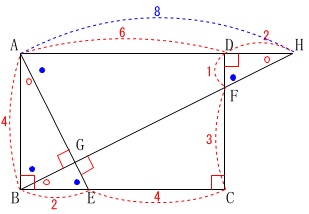となっているので、
　\(\,\mathrm{△HDF}\,\)∽\(\,\mathrm{△HGA}\,\)
であり、
　\(\,\mathrm{∠AGH=90^{\circ}}\,\)

このとき
　\(\,\mathrm{∠AGF=∠EGF=90^{\circ}}\,\)
を円周角とするので
　\(\,\mathrm{AF}\,\)と\(\,\mathrm{EF}\,\)は直径
であることが分かります。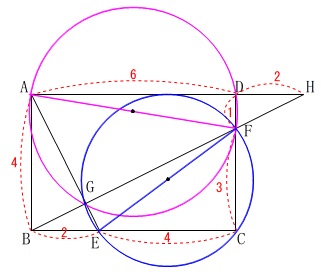
円の相似比は半径でも直径でも同じなので、
直径の比を求め、\(\,2\,\)乗した比が面積比になります。
　相似比　\(\,a:b\,\)
　面積比　\(\,a^2:b^2\,\)

\(\,\mathrm{△ADF}\,\)において三平方の定理から
　\(\begin{eqnarray}
\mathrm{AF^2}&=&\mathrm{AD^2+DF^2}\\
&=&6^2+1^2\\
&=&\color{magenta}{37}
\end{eqnarray}\)
（面積比を出すので\(\,2\,\)乗のままにしておきます。）

\(\,\mathrm{△EGF}\,\)において三平方の定理から
　\(\begin{eqnarray}
\mathrm{EF^2}&=&\mathrm{CF^2+CE^2}\\
&=&3^2+4^2\\
&=&\color{blue}{25}
\end{eqnarray}\)

よって、円の面積比は
　\(\hspace{4pt}\color{magenta}{37}:\color{blue}{25}\)

答え　\(\displaystyle \underline{　\frac{37}{25}　倍}\)

\(\,\mathrm{AE}\,\)⊥\(\,\mathrm{AF}\,\)のときも、
2つの円の直径を求めるときも、
直角三角形は他にもたくさんありますので気がつけばどれでも良いです。
長さのややこしい三角形を選ぶと時間がかかるというだけです。

ただ、円の面積が\(\,\pi\,r^2\,\)なので、
面積の比は半径からしか出てこない、
つまり、
半径（または直径）を求めに行くことがポイントになるということは覚えておくと良いです。

(3)
四角錐の体積と、点と面との距離を求めます。

これは(2)に比べると簡単ですが、
引っかけ、ともいうところがあるので注意しておきましょう。

立体は正四角すいです。
　\(\,\mathrm{OA=9}\,\)
　\(\,\mathrm{AB=6}\,\)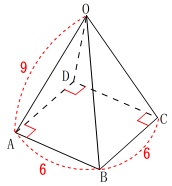高さは\(\,\mathrm{O}\,\)から正方形\(\,\mathrm{ABCD}\,\)に下ろした垂線の長さになります。

垂線と正方形\(\,\mathrm{ABCD}\,\)との交点を\(\,\mathrm{H}\,\)とすると、
\(\,\mathrm{\color{blue}{OH}}\,\)が高さです。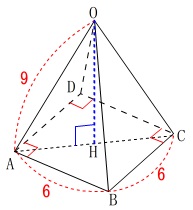底面を抜き出すと、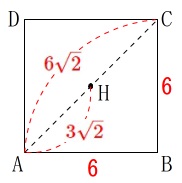
\(\,\mathrm{AH}\,\)はすぐに求まるので三平方の定理から
　\(\begin{eqnarray}
\mathrm{OH^2}&=&\mathrm{OA^2-AH^2}\\
&=&9^2-(3\sqrt{2})^2\\
&=&81-18\\
&=&63\\
\mathrm{OH}&=&\color{blue}{3\sqrt{7}}　（\,＞\,0\,)
\end{eqnarray}\)

よって、求める四角すいの体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \color{red}{6}^2\times \color{blue}{3\sqrt{7}}\\
&=&\underline{　36\sqrt{7}　(\,\mathrm{cm^3}\,)}
\end{eqnarray}\)

②
頂点\(\,\mathrm{A}\,\)と平面\(\,\mathrm{OBC}\,\)との距離を求めます。

問題で「平面\(\,\mathrm{OBC}\,\)」と書いてあるのは、
\(\,\mathrm{A}\,\)から下ろした垂線と交わるのが\(\,\mathrm{△OBC}\,\)の外部でも距離にあることを言っているのですが、
実は垂線がどこに下りるかは関係ありません。

四角すい\(\,\mathrm{OABCD}\,\)の体積の半分である、
三角すい\(\,\mathrm{O-ABC}\,\)を考えます。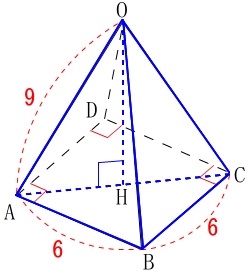
三角すい\(\,\mathrm{O－ABC}\,\)の体積\(\,V_1\,\)は、
正四角すい\(\,\mathrm{OABCD}\,\)の体積\(\,V\,\)の半分なので
　\(\begin{eqnarray}\displaystyle
\color{magenta}{V_1}&=&\frac{1}{2}\times V\\
&=&\frac{1}{2}\times 36\sqrt{7}\\
&=&\color{magenta}{18\sqrt{7}}
\end{eqnarray}\)

今度は底面を\(\,\mathrm{△OBC}\,\)として三角すい\(\,\mathrm{A-OBC}\,\)と見ると、
底面\(\,\mathrm{OBC}\,\)は二等辺三角形で

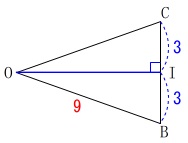
底面\(\,\mathrm{OBC}\,\)の面積\(\,S\,\)は高さ\(\,\mathrm{OI}\,\)が
　\(\begin{eqnarray}\displaystyle
\mathrm{OI}&=&\sqrt{81-9}\\
&=&\sqrt{72}\\
&=&6\sqrt{2}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
\color{red}{S}&=&\frac{1}{2}\times 6\times 6\sqrt{2}\\
&=&\color{red}{18\sqrt{2}}
\end{eqnarray}\)

転がしても三角すいの体積は変わらないので、
\(\,\mathrm{A}\,\)から平面\(\,\mathrm{OBC}\,\)までの距離を\(\,\color{blue}{h}\,\)とすると
　\(\begin{eqnarray}\displaystyle
\color{magenta}{V_1}&=&\frac{1}{3}\times \color{red}{S}\times \color{blue}{h}\\
\color{magenta}{18\sqrt{7}}&=&\frac{1}{3}\times \color{red}{18\sqrt{2}}\times \color{blue}{h}\\
\color{blue}{h}&=&\frac{18\sqrt{7}}{6\sqrt{2}}\\
&=&\frac{3\sqrt{7}}{\sqrt{2}}\\
&=&\underline{　\frac{3\sqrt{14}}{2}　(\,\mathrm{cm}\,)}
\end{eqnarray}\)

\(\,\mathrm{A}\,\)から面\(\,\mathrm{OBC}\,\)に下ろした垂線がどこに行くのかを見ておきます。

正方形\(\,\mathrm{ABCD}\,\)を底面とする直方体を考えると、
面\(\,\mathrm{OBC}\,\)は側面を斜めに切ります。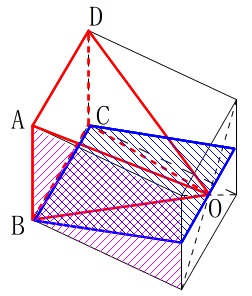このとき面\(\,\mathrm{ABCD}\,\)と面\(\,\mathrm{OBC}\,\)は垂直にはなりませんが、
面\(\,\mathrm{\color{blue}{OBC}}\,\)と\(\,\color{magenta}{直方体の側面}\,\)は垂直になります。

よって\(\,\mathrm{A}\,\)から面\(\,\mathrm{OBC}\,\)に下ろした垂線は側面上にあり、
側面の横の長さは\(\,\mathrm{OH=3\sqrt{7}}\,\)に等しいので、
側面上の点を\(\,\mathrm{L,M,N}\,\)とすると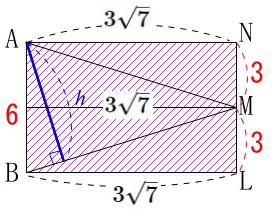
　\(\begin{eqnarray}\displaystyle
\mathrm{AM}&=&\mathrm{BM}\\
&=&\sqrt{(3\sqrt{7})^2+3^2}\\
&=&\sqrt{63+9}\\
&=&\sqrt{72}\\
&=&\color{blue}{6\sqrt{2}}
\end{eqnarray}\)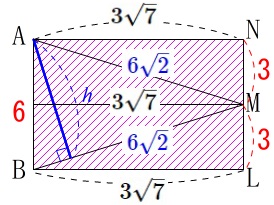
側面上で\(\,\mathrm{△ABM}\,\)の面積は\(\,\color{magenta}{S_1}\,\)は
　\(\begin{eqnarray}\displaystyle
\color{magenta}{S_1}&=&\frac{1}{2}\times \color{red}{6}\times 3\sqrt{7}\\
&=&\color{magenta}{9\sqrt{7}}
\end{eqnarray}\)

また、
三角形の面積\(\,\color{red}{S_1}\,\)は\(\,\mathrm{BM}\,\)を底辺とし、
高さを\(\,\color{blue}{h}\,\)とする三角形でもあるので、
　\(\begin{eqnarray}\displaystyle
\color{magenta}{S_1}&=&\frac{1}{2}\times 6\sqrt{2}\times \color{blue}{h}\\
\color{magenta}{9\sqrt{7}}&=&\frac{1}{2}\times 6\sqrt{2}\times \color{blue}{h}\\
h&=&\frac{9\sqrt{7}}{3\sqrt{2}}\\
&=&\underline{　\frac{3\sqrt{14}}{2}　}
\end{eqnarray}\)

とすることもできます。

この問題は位置を確認しなくても、（できなくても）
計算で答えが出ることを前提に「平面」として条件を与えてくれているのでしょう。

\(\,2020\,\)年愛知県公立高校入試\(\,\mathrm{A}\,\)問題の数学は以上です。

途中の説明を少なくしても割と長くなりました。
\(\,45\,\)分で解く問題ですので、迷うヒマ無く条件を書き出し、計算し続けなければ間に合わないでしょう。

2021年度愛知県公立入試数学の削除項目

愛知県の\(\,2021\,\)年度の公立入試において、
削除項目はありません。

\(\,3\,\)年分の学習は終える授業時間が確保できているそうです。

それでも定着させる時間は不足すると予想できるので、
自分で何度も何度も繰り返し復習しておくようにしましょう。

⇒　2020年愛知県公立高校入試B日程の数学問題の解説

\(\,\mathrm{B}\,\)日程も問題構成は同じです。
もちろん求められるのも変わりません。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

例年\(\,\mathrm{B}\,\)問題も同じような問題構成です。

教科書の基礎から少し標準的な問題まで繰り返しておくと良いですね。