2020年愛知県公立高校入試B日程の数学問題の解説

2020年(令和2年）に愛知県で行われた公立高校入試B日程の数学問題の解説です。
愛知県の入試では誘導が少ないので解法がいろいろ考えられますが、思い立った方法で突っ走りましょう。
A日程問題よりは得点しやすですが、手を止めたらそこで終わることはどこでも変わりません。

2020年愛知県公立高校入試B日程の数学の問題

問題は\(\,\mathrm{A}\,\)日程\(\,\mathrm{B}\,\)日程ともに大問3つです。

⇒　2020年愛知県公立高校入試B日程の数学の問題

\(\,3\,\)問は決して少なくない質と量ですが気づきが必要になります。
数学で気がつくことは作業しないと出てこないことですよ。

傾向は\(\,\mathrm{A}\,\)問題で見て頂くことにして、
作業しまくれば出てくる標準的な解法で簡単に、できるだけ短く、解説しておきます。

2020年愛知県公立高校入試B日程の数学の問題の解説

式の計算、方程式、文章題、関数、図形とすべての分野から偏り無く出題されています。
公立入試としては当然ですが、全体が標準的なレベルで出題されているのが愛知県の特徴です。

\(\,\mathrm{A}\,\)日程の解説でも書いておきましたが、
２０２１年度の公立入試では削除項目はありません。
例年通りです。

注意点などは\(\,\mathrm{A}\,\)日程の解説と同じことの繰り返しになるので、
\(\,\mathrm{A}\,\)日程の解説に目を通しておいてください。

第１問

\(\,\large{1}\,\)

小問題集合です。

(1)符号だけには注意しておきましょう。
　\(\hspace{10pt}4-6\div (-2)\\
=4+3\\
=\underline{　7　}\)

(2)展開です。
　\(\hspace{10pt}(2x+1)(3x-1)-(2x-1)(3x+1)\\
=6x^2+x-1-(6x^2-x-1)\\
=6x^2+x-1-6x^2+x+1\\
=\underline{　2x　}\)

共通因数がないので楽にはなりません。
ミスを防ぐためにも\(\,2\,\)行目は抜かさない方が良いです。

まとまりがあるので
　\(\hspace{10pt}(a+1)(b-1)-(a-1)(b+1)\\
=ab-a+b-1-(ab+a-b-1)\\
=ab-a+b-1-ab-a+b+1\\
=2b\)
とすればきれいには見えますが、何も変わっていません。笑
素直に展開した方が早いです。

(3)
　\(\hspace{10pt}(\sqrt{5}-1)^2+\sqrt{20}\\
=5-2\sqrt{5}+1+2\sqrt{5}\\
=\underline{　6　}\)

部分的に
　\(\hspace{10pt}(\sqrt{5}-1)^2\\
=6-2\sqrt{2}\)
を暗算するのは良いですけど、
全体でミスはしたくないので慎重に行きましょう。

(4)方程式の解を求めます。
　\(\begin{eqnarray}
(\color{red}{x+1})(x-1)&=&3(\color{red}{x+1})\\
(\color{red}{x+1})(x-1-3)&=&0\\
(x+1)(x-4)&=&0\\
x&=&\underline{　-1\,,\,4　}
\end{eqnarray}\)

共通因数があったので因数分解に利用しましたが、
展開してからでもいいです。
　\(\begin{eqnarray}
(x+1)(x-1)&=&3(x+1)\\
x^2-1&=&3x+3\\
x^2-3x-4&=&0\\
(x+1)(x-4)&=&0
\end{eqnarray}\)
たいして変わりません。

(5)
買い物した代金より出したお金の方が多いからおつりが来ます。

　\(\hspace{10pt}\underline{　5a+b\,＜\,500　}\)

(6)
生徒の人数をどうやっておくかで変わりますがどうでもいいです。
最初に希望した人数が
　\(\,\mathrm{A:B=1:2}\,\)
なので
　\(\,\mathrm{A}\,;　x　,　\mathrm{B}\,;　2x\,\)
とします。

\(\,14\,\)人が\(\,\mathrm{B}\,\)から\(\,\mathrm{A}\,\)に変更したので
変更後の人数は
　\(\,\mathrm{A}\,;　x+14\,\)
　\(\,\mathrm{B}\,;　2x-14\,\)
この比が\(\,5:7\,\)なので
　\(\begin{eqnarray}
(x+14):(2x-14)&=&5:7\\
5(2x-14)&=&7(x+14)\\
10x-70&=&7x+98\\
3x&=&\underline{　168　(人)}
\end{eqnarray}\)

お伝えするのを忘れていました。
生徒の人数は\(\,3x\,\)です。

もちろん\(\,x\,\)を求めて\(\,\mathrm{A,B}\,\)の最初の人数を出して加えても良いです。
ただし、何を求めるかは確認していおきましょう。

(7)
関数の性質を聞かれているならグラフは描いて考えましょう。
簡単なグラフで良いですよ。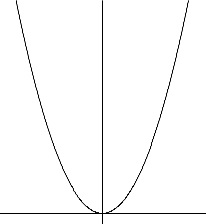
ア
\(\,x\,\)が負の範囲(\(\,y\,\)軸より左）では、\(\,x\,\)が増加したら\(\,y\,\)は減少します。
イ
\(\,y\,\)軸対称です。
ウ
\(\,-1≦x≦2\,\)での最小値は\(\,0\,\)です。
エ
\(\,y\,\)の値が負になることはありません。

　答え　\(\,\underline{　イ　エ　}\,\)

(8)
資料を見るときは値が小さい順に並べてみるのが基本です。
　\(18\,,\,20\,,\,\color{red}{23}\,|\,\color{blue}{25}\,,\,26\,,\,26\)

中央値は小さい順に並べたとき真ん中の順位にある値ですが、
データの数が偶数のときは中央2つの平均が中央値になります。

　\(\hspace{10pt}\displaystyle \frac{\color{red}{23}+\color{blue}{25}}{2}\\
=\underline{　24　(\,\mathrm{m}\,)}\)

(9)
円周角と二等辺三角形の性質を使って角度を求めます。
　\(\hspace{4pt}\mathrm{∠ABO}=31^{\circ}\)
　\(\hspace{4pt}\mathrm{∠BOC}=154^{\circ}\)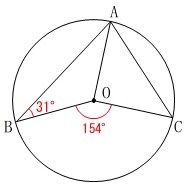円周角が中心角の半分であること、
半径は等しいから二等辺三角形であることから、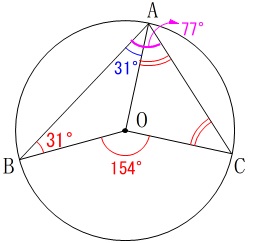
　\(\begin{eqnarray}
\mathrm{∠ACO}&=&\mathrm{∠CAO}\\
&=&\color{magenta}{77^{\circ}}-\color{blue}{31^{\circ}}\\
&=&46^{\circ}
\end{eqnarray}\)

答え　\(\,\underline{　46　度}\,\)

第２問

\(\,\large{2}\,\)
確率、規則的な数値計算、三角形の\(\,2\,\)等分、\(\,1\,\)次関数の文章題の\(\,4\,\)問です。

(1)
さいころを\(\,\mathrm{2}\,\)回投げる確率です。

さいころを投げて出た目の約数のカードを取り除き、
\(\,\mathrm{2}\,\)回投げた後、
カードが\(\,1\,\)枚だけ残る確率を求めます。

樹形図で良いですが、表でも良いです。

\(\,\mathrm{1}\,\)から\(\,\mathrm{6}\,\)の約数を見ると、
2つの数字の約数で5つの数字が取り除かれる必要があるので、
\(\,\mathrm{6}\,\)は必ず出なくてはならない、と気がつけば早いです。

そのことに気がつくのは約数を書き出した後です。
問題に「さいころの出た目の約数」と書いてあるんだから約数は書き出しましょう。
　\(\,\mathrm{1：1}\,\)
　\(\,\mathrm{2：1,2}\,\)
　\(\,3：1,3\,\)
　\(\,4：1,2,4\,\)
　\(\,5：1,5\,\)
　\(\,6：1,2,3,6\,\)

見にくいので見やすくします。
（黒字が約数です。）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\color{blue}{1} & 1 & & & & & \\ \hline
\color{blue}{2} & 1 & 2 & & & & \\ \hline
\color{blue}{3} & 1 & & 3 & & & \\ \hline
\color{blue}{4} & 1 & 2 & & 4 & & \\ \hline
\color{blue}{5} & 1 & & & & 5 & \\ \hline
\color{blue}{6} & 1 & 2 & 3 & & & 6\\ \hline
\end{array}\)

2つの約数を重ねて残りが1つになる組み合わせを考えますが、
　\(\,4\,\)と\(\,6\,\)　か　\(\,5\,\)と\(\,6\,\)
の場合だけですね。

確率は表で求めておきます。
（一回目は青でも赤でもどちらでも良いです。）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6}\\ \hline
\color{blue}{1} & & & & & & \\ \hline
\color{blue}{2} & & & & & & \\ \hline
\color{blue}{3} & & & & & & \\ \hline
\color{blue}{4} & & & & & & ○\\ \hline
\color{blue}{5} & & & & & & ○\\ \hline
\color{blue}{6} & & & & ○ & ○ & \\ \hline
\end{array}\)

答え　\(\displaystyle \frac{4}{36}=\underline{　\frac{1}{9}　}\)

(2)
数値計算を規則的に繰り返し、
\(\,7\,\)回で結果が\(\,1\,\)となる元の数を求めます。

計算規則（ルール）は、
　操作\(\,\mathrm{A}\,\)：奇数なら\(\,3\,\)倍して\(\,1\,\)を加える。
　操作\(\,\mathrm{B}\,\)：偶数ならば\(\,2\,\)で割る。
　\(\,7\,\)回繰り返し結果が\(\,1\,\)となる。

問題が例を与えてくれています。
　与えられた数が\(\,\color{red}{3}\,\)のとき
　\(\,\color{red}{①}\,\)\(\hspace{4pt}3\times 3+1\,=10\)
　\(\,\color{blue}{②}\,\)\(\hspace{4pt}10\div 2\,=5\)
　\(\,\color{red}{③}\,\)\(\hspace{4pt}5\times 3+1\,=16\)
　\(\,\color{blue}{④}\,\)\(\hspace{4pt}16\div 2\,=8\)
　\(\,\color{blue}{⑤}\,\)\(\hspace{4pt}8\div 2\,=4\)
　\(\,\color{blue}{⑥}\,\)\(\hspace{4pt}4\div 2\,=2\)
　\(\,\color{blue}{⑦}\,\)\(\hspace{4pt}2\div 2\,=1\)

　与えられた数が\(\,\color{blue}{128}\,\)のとき
　\(\,\color{blue}{①}\,\)\(\hspace{4pt}128\div 2\,=64\)
　\(\,\color{blue}{②}\,\)\(\hspace{4pt}64\div 2\,=32\)
　\(\,\color{blue}{③}\,\)\(\hspace{4pt}32\div 2\,=16\)
　\(\,\color{blue}{④}\,\)\(\hspace{4pt}16\div 2\,=8\)
　\(\,\color{blue}{⑤}\,\)\(\hspace{4pt}8\div 2\,=4\)
　\(\,\color{blue}{⑥}\,\)\(\hspace{4pt}4\div 2\,=2\)
　\(\,\color{blue}{⑦}\,\)\(\hspace{4pt}2\div 2\,=1\)

上の例を見ていれば分かるように、
自然数なので\(\,\color{blue}{⑦}\,\)で\(\,1\,\)となるのは\(\,2\,\)だけです。
\(\,\color{blue}{⑥}\,\)で\(\,2\,\)となるのは\(\,4\,\)だけです。
\(\,\color{blue}{⑤}\,\)で\(\,4\,\)となるのは\(\,1\,\)と\(\,8\,\)ですが、
\(\,1\,\)になったら計算は終わるので\(\,7\,\)回で終わりません。
だから\(\,8\,\)だけです。
\(\,\color{blue}{④}\,\)で\(\,8\,\)になるのは\(\,16\,\)だけです。
\(\,\color{magenta}{③}\,\)で\(\,16\,\)になるのは\(\,\color{red}{5}\,\)と\(\,\color{blue}{32}\,\)の2つがあります。

つまり、逆にたどれば\(\,\color{blue}{⑦}\,\)から\(\,\color{blue}{④}\,\)までは、
変化しないで\(\,③\,\)の結果は\(\,16\,\)ということです。

ここで\(\,③\rightarrow ②\rightarrow ①\,\)の順に逆戻りしてみましょう。
　\(\begin{array}{|c|c|c|c|} \hline
③の結果 & ②の結果 & ①の結果 & 元\\ \hline
16 & \color{blue}{32} & \color{blue}{64} & \color{blue}{128} \\ \hline
16 & \color{blue}{32} & \color{blue}{64} & \color{red}{21} \\ \hline
16 & \color{red}{5} & \color{blue}{10} & \color{blue}{20} \\ \hline
16 & \color{red}{5} & \color{blue}{10} & \color{red}{3} \\ \hline
\end{array}\)

条件を満たす
　操作\(\,\mathrm{A}\,\)：奇数なら\(\,3\,\)倍して\(\,1\,\)を加える。
　操作\(\,\mathrm{B}\,\)：偶数ならば\(\,2\,\)で割る。
組み合わせは4つしかありません。

答え　\(\,\underline{　a　20　b　21　}\,\)

問題に小さい順に並べると\(\,3\,\)と\(\,128\,\)の間に2つあると書いてあるので、
\(\,4\,\)から\(\,127\,\)の\(\,124\,\)個の自然数を調べれば終わりますが、
かけて、足して、を繰り返している内に途中で規則性に気がつくでしょう。

(3)
三角形の面積を\(\,2\,\)等分する直線と、
もう一つの直線の交点を求めます。

三角形の頂点を通る直線ではないので、
具体的な面積を求めて等分する方法が考えられますが、
この問題は具体的な面積を求める必要はありません。

ながめているだけでは先に進まないので、
条件の整理をしておきましょう。

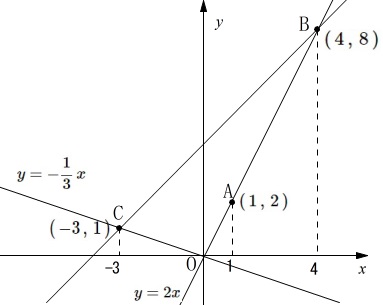
　\(\,\mathrm{A,B}\,\)は\(\,y=2x\,\)上の点
　\(\,\mathrm{C}\,\)は\(\,\displaystyle y=-\frac{1}{3}\,x\,\)上の点
　\(\,\mathrm{A,B,C}\,\)の\(\,x\,\)座標はそれぞれ\(\,1,4,-3\,\)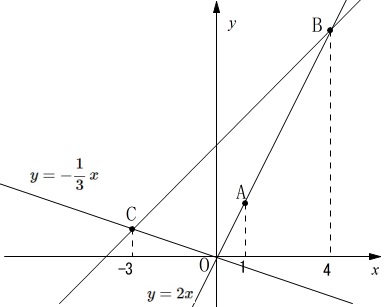座標を求めておきます。
　\(\,\mathrm{A\,(\,1\,,\,2\,)}\,\)
　\(\,\mathrm{B\,(\,4\,,\,8\,)}\,\)
　\(\,\mathrm{C\,(\,-3\,,\,1\,)}\,\)
必要無くても（利用するかどうか分からなくても）出しておくべきでしょう。
直線\(\,\mathrm{BC}\,\)の式も求めておきます。

　\(\,\mathrm{B\,(\,4\,,\,8\,)}\,\)
　\(\,\mathrm{C\,(\,-3\,,\,1\,)}\,\)
を通るので
　\(\hspace{4pt} y=x+4\)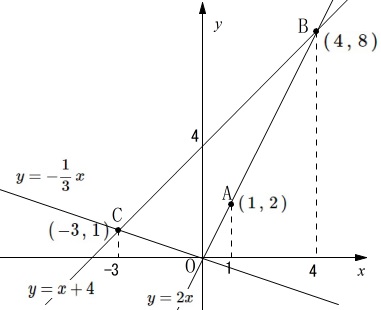
直線が\(\,\mathrm{A}\,\)を通り\(\,\mathrm{△OBC}\,\)の面積を\(\,2\,\)等分するとき、
線分\(\,\mathrm{BC}\,\)上のどこかと交わります。

目安をつけておきます。
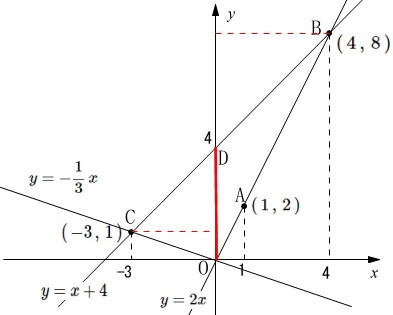直線\(\,\mathrm{BC}\,\)の\(\,y\,\)切片が\(\,4\,\)なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△OBC}&=&\mathrm{\color{red}{△OCD}+\color{blue}{△OBC}}\\
&=&\frac{1}{2}\times 4\times 3+\frac{1}{2}\times 4\times 4\\
&=&\color{red}{6}+\color{blue}{8}\\
&=&14
\end{eqnarray}\)

これを面積\(\,7\,\)と\(\,7\,\)に\(\,2\,\)等分すれば良いことになります。

　\(\begin{eqnarray}\displaystyle
\mathrm{△OAD}&=&\frac{1}{2}\times 4\times 1\\
&=&2
\end{eqnarray}\)
なので\(\,\mathrm{D}\,\)よりは\(\,\mathrm{C}\,\)側の点で交わることは分かります。
※
交点が\(\,\mathrm{D}\,\)のときは\(\,\mathrm{△OAD}\,\)の分四角形に移るので、
　\(\mathrm{△ABD}=\,\color{blue}{8}-2\,=6\)
となってしまいます。

では交点を求めましょう。
方法はいくつかありますが、
直線\(\,\mathrm{BC}\,\)上の交点を
　\(\hspace{4pt}(\,t\,,\,t+4\,)\)
とおいて座標を使って面積計算すると早いのですが一般的ではないので、
普通に解いておきます。
（というか、この問題に時間をかけている場合ではない。）

直線\(\,x=1\,\)と直線\(\,\mathrm{BC}\,\)\(\,(\,y=x+4\,)\,\)との交点は
　\(\hspace{4pt}\mathrm{E}\,(\,1\,,\,5\,)\)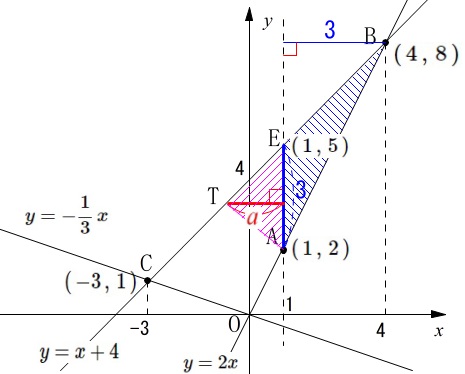ここで\(\,\mathrm{A}\,\)を通る直線と\(\,\mathrm{BC}\,\)が交わる点が\(\,\mathrm{T}\,\)だとすると、
\(\,\mathrm{△ABT=7}\,\)となれば良いので、
　\(\mathrm{\color{blue}{△ABE}+\color{magenta}{△ATE}}=7\)

部分的に面積を求めておくと
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△ABE}}&=&\frac{1}{2}\times 3\times 3\\
&=&\color{blue}{\frac{9}{2}}
\end{eqnarray}\)
なので\(\,\mathrm{△ATE}\,\)の面積が
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△ATE}}&=&7-\color{blue}{\frac{9}{2}}\\
&=&\color{magenta}{\frac{5}{2}}
\end{eqnarray}\)
となれば良いので\(\,\mathrm{△ATE}\,\)の高さを\(\,\color{red}{a}\,\)とすると
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times 3\times a&=&\frac{5}{2}\\
a&=&\color{red}{\frac{5}{3}}
\end{eqnarray}\)

このことから\(\,\mathrm{T}\,\)の\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle x&=&1-\color{red}{\frac{5}{3}}\\
\displaystyle &=&-\frac{2}{3}
\end{eqnarray}\)

このとき\(\,\mathrm{T}\,\)の\(\,y\,\)座標は\(\,y=x+4\,\)から
　\(\begin{eqnarray}\displaystyle
y&=&-\frac{2}{3}+4\\
&=&\frac{10}{3}
\end{eqnarray}\)

よって求める交点の座標は
　\(\displaystyle \underline{　\left(\,-\frac{2}{3}\,,\,\frac{10}{3}\,\right)　}\)

または高さ\(\,\color{red}{a}\,\)を求めるのは
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE+△ATE}&=&7\\
\frac{1}{2}\times 3\times (\color{blue}{3}+\color{red}{a})&=&7\\
3(3+a)&=&14\\
9+3a&=&14\\
a&=&\frac{5}{3}
\end{eqnarray}\)
とまとめても良いです。

図形の性質を利用しても良いですね。

\(\,\mathrm{△OBC}\,\)の底辺を\(\,\mathrm{OB}\,\)と見ると、
　\(\,\mathrm{OA:AB=\color{red}{1}:\color{red}{4}}\,\)
なので、
　\(\mathrm{△OAC:△ACT:△ABT}=\color{magenta}{1}:\color{magenta}{1}:\color{magenta}{2}\)
となるように\(\,\mathrm{T}\,\)をとれば良いので
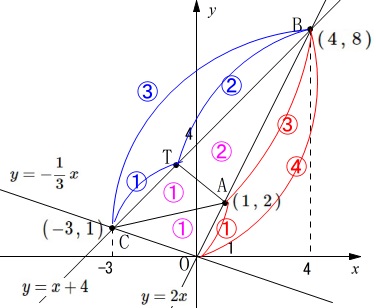　\(\hspace{4pt}\mathrm{CT:TB}=\color{blue}{1}:\color{blue}{2}\)
となることから交点を求めても良いです。
※
会員は\(\,\mathrm{△ABT}\,\)が\(\,\mathrm{△OBC}\,\)の半分になることから
　\(\displaystyle \mathrm{\frac{AB}{OB}\times \frac{TB}{CB}}=\frac{1}{2}\)
を利用したかもしれませんが構いません。
使える事実はどんどん使いましょう。

座標を用いた解法は省略します。

(4)
時間と容器に入った水の高さの問題です。

文章を読み取れれば難しくはありませんので、
落ち着いて条件を処理すると良いです。

　ポンプ\(\,\mathrm{P}\,\)は\(\,\mathrm{A\rightarrow C}\,\)
　ポンプ\(\,\mathrm{P}\,\)は\(\,\mathrm{B\rightarrow C}\,\)
　\(\,\mathrm{A\rightarrow C}\,\)は毎分\(\,\mathrm{2\,cm}\,\)
　\(\,\mathrm{B\rightarrow C}\,\)は毎分\(\,\mathrm{1\,cm}\,\)
　ポンプは同時に動かしはじめる。

ここまでは全体にる条件ですが、
①②では\(\,\mathrm{A,B}\,\)に入っている水の量は違いますので注意しましょう。

①
ポンプの止まる時間差を求めます。

　\(\,\mathrm{A}\,\)の水の高さは\(\,\mathrm{\color{red}{40}}\,\)
　\(\,\mathrm{P,Q}\,\)同時に動かして両方止まったとき\(\,\mathrm{C}\,\)の高さが\(\,\color{blue}{75}\,\)

どちらが先に止まるかを考えます。
（高さの単位を省略します。）

\(\,\mathrm{A}\,\)にあるのは\(\,\color{red}{40}\,\)、全体で\(\,\color{blue}{75}\,\)なので、
\(\,\mathrm{B}\,\)に入っていた水は
　\(\hspace{10pt}\color{red}{70}-\color{blue}{45}\,=35\,\)

　\(\,\mathrm{A\rightarrow C}\,\)は毎分\(\,\mathrm{2\,cm}\,\)
なので\(\,\mathrm{A}\,\)の水を\(\,\mathrm{C}\,\)に移すのにかかった時間は
　\(\hspace{4pt}\displaystyle \frac{40}{2}=20　(分)\)

　\(\,\mathrm{B\rightarrow C}\,\)は毎分\(\,\mathrm{1\,cm}\,\)
なので\(\,\mathrm{B}\,\)の水を\(\,\mathrm{C}\,\)に移すのにかかった時間は
　\(\hspace{4pt}35　(分)\)

よって、\(\,\mathrm{A}\,\)が先に止まり、
\(\,\mathrm{B}\,\)が止まったのは
　\(\hspace{10pt}35-20\,=\underline{　15　(分後)}\)

②
時間と水の高さとの関係をグラフにします。
\(\,\mathrm{A,B}\,\)に入っている水の量は分かっていません。

分かっているのは
　\(\,25\,\)分後の高さが\(\,45\,\)
　\(\,50\,\)分後の高さが\(\,65\,\)
座標で表すと
　\(\,(\,25\,,\,45\,)\,\)
　\(\,(\,50\,,\,65\,)\,\)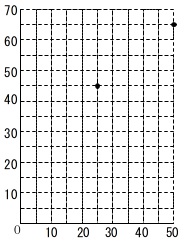
　最初は両方ポンプが動いていて傾きが\(\,3\,\)
　ポンプ\(\,\mathrm{P}\,\)だけが動けば傾き\(\,2\,\)
　ポンプ\(\,\mathrm{Q}\,\)だけが動けば傾き\(\,1\,\)
の直線になります。

ここで\(\,\mathrm{Q}\,\)が先に止まったとすると、
\(\,\mathrm{P}\,\)だけが\(\,25\,\)分動いた場合、
高さは少なくとも\(\,50\,\)を超えるので、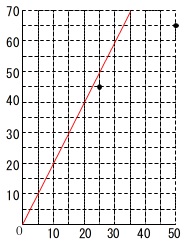
先に止まるのは\(\,\mathrm{P}\,\)です。

\(\,\mathrm{P}\,\)が止まり
\(\,\mathrm{Q}\,\)だけが動いた場合は傾きは\(\,1\,\)なので
　\(\hspace{4pt}y=x+b\)
という直線で\(\,(\,25\,,\,45\,)\,\)を通ります。
（傾き\(\,2\,\)の直線だけが表れることは無いということです。）

\(\,\mathrm{Q}\,\)だけでも\(\,(\,25\,,\,45\,)\,\)は通らないので
最初は両方動いていて傾き\(\,3\,\)の比例関数で
　\(\hspace{10pt}y=3x\)
途中から\(\,\mathrm{Q}\,\)だけが動いて傾き\(\,1\,\)の直線になり、
　\(\,(\,25\,,\,45\,)\,\)
を通り、高さ\(\,50\,\)までは動くということになります。
（\(\,\mathrm{P}\,\)はすでに止まっています。）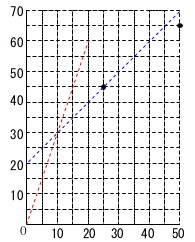
\(\,50\,\)分後\(\,65\,\)を超えることはないので、
\(\,45\,\)分後からは高さは変わりません。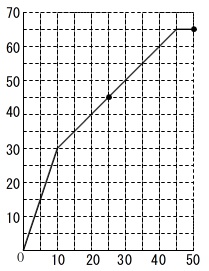\(\,\mathrm{A,B}\,\)に入っていた水の高さも求めることはできますが、
聞かれていないので考え無くて良いです。
　\(\,\mathrm{A：20cm}\,\)
　\(\,\mathrm{B：45cm}\,\)

\(\,\large{2}\,\)に時間をかけ過ぎましたが以上です。

\(\,\large{3}\,\)は図形です。

第３問

\(\,\large{3}\,\)

\(\,3\,\)は角度、線分、面積、体積と図形総合問題です。
具体的な角度、長さがあるので次から次へと分かるところを追っていきましょう。

(1)
条件に合う角度を求めます。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{DF}\,\)は\(\,\mathrm{∠ADC}\,\)の二等分線
　\(\,\mathrm{AE}\,\)⊥\(\,\mathrm{DF}\,\)
　\(\,\mathrm{∠FEB=56^{\circ}}\,\)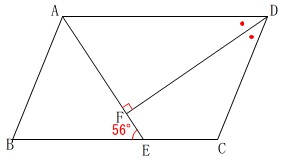平行線の錯角は等しいので、
　\(\hspace{4pt}\mathrm{∠AEB=∠EAD=\color{red}{56^{\circ}}}\)
三角形の内角の和から
　\(\hspace{4pt}\mathrm{∠ADF=\color{blue}{34^{\circ}}}\)
\(\,\mathrm{DF}\,\)は角の二等分線だから
　\(\hspace{4pt}\mathrm{∠CDF=\color{blue}{34^{\circ}}}\)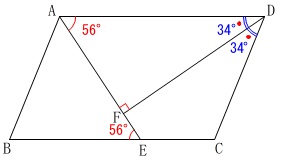平行四辺形の対角は等しいので
　\(\hspace{4pt}\mathrm{∠ABE=\color{blue}{68^{\circ}}}\)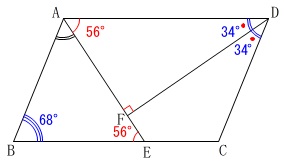よって、三角形の内角の和から
　\(\begin{eqnarray}
\mathrm{∠BAF}&=&180^{\circ}-(\mathrm{\color{blue}{∠ABE}+\color{red}{∠AEB}})\\
&=&180^{\circ}-(\color{blue}{68^{\circ}}+\color{red}{56^{\circ}})\\
&=&56^{\circ}
\end{eqnarray}\)

答え　\(\,\underline{　56　度}\,\)

平行四辺形の隣り合う\(\,\mathrm{2}\,\)角の和が\(\,\mathrm{180^{\circ}}\,\)でも、
分かる角度を追っていけば何でもいいです。

(2)
線分の長さを求めます。

条件
　\(\,\mathrm{ABCD}\,\)は台形
　\(\,\mathrm{E}\,\)は\(\,\mathrm{AB}\,\)の中点
　\(\,\mathrm{AEFD}\,\)と\(\,\mathrm{EBCF}\,\)の周の長さが等しい。
　\(\,\mathrm{AD=2}\,\)
　\(\,\mathrm{BC=6}\,\)
　\(\,\mathrm{DC=5}\,\)
　台形\(\,\mathrm{ABCD}\,\)の高さは\(\,4\,\)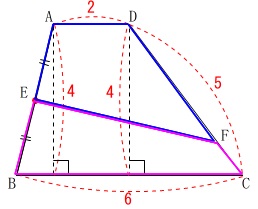これだけ条件があれば何でも出そうですが、
問題に合わせて行きます。

①
線分\(\,\mathrm{DF}\,\)の長さを求めます。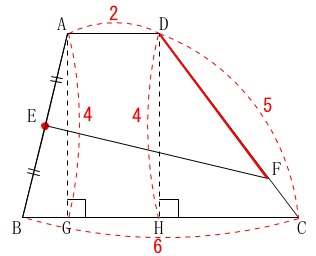
　\(\,\mathrm{AEFD}\,\)と\(\,\mathrm{EBCF}\,\)の周の長さが等しい。
　\(\,\mathrm{E}\,\)は\(\,\mathrm{AB}\,\)の中点
という条件と、\(\,\mathrm{EF}\,\)が共通であることから、
　\(\hspace{4pt}\mathrm{AD+DF=BC+CF}\)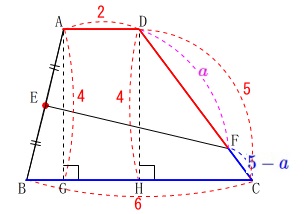
ここで\(\,\mathrm{DF}=\color{magenta}{a}\,\)とすると、
　\(\begin{eqnarray}\displaystyle
\mathrm{AD+DF}&=&\mathrm{BC+CF}\\
2+\color{magenta}{a}&=&6+(\color{blue}{5-a})\\
2a&=&9\\
a&=&\underline{　\frac{9}{2}　\mathrm{cm}}
\end{eqnarray}\)

②
四角形\(\,\mathrm{EBCF}\,\)の面積を求めます。
公式が使える形をしていないので、全体から部分を引きましょう。

\(\,\mathrm{AD}\,\)∥\(\,\mathrm{EK}\,\)となるように\(\,\mathrm{DC}\,\)上に\(\,\mathrm{K}\,\)をとると、
中点連結定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{EK}&=&\frac{\mathrm{AD+BC}}{2}\\
&=&\frac{2+6}{2}\\
&=&\color{blue}{4}　･･･\color{red}{★}
\end{eqnarray}\)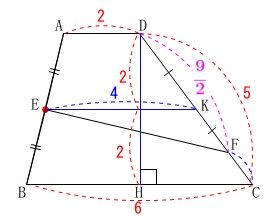なので台形\(\,\mathrm{EBCK}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{(\,\color{blue}{4}+\color{red}{6}\,)\times \color{red}{2}}{2}\\
&=&\color{red}{10}
\end{eqnarray}\)

これから\(\,\mathrm{△EKF}\,\)を引きましょう。

①から\(\,\displaystyle \mathrm{DF}=\color{magenta}{\frac{9}{2}}\,\)なので\(\,\mathrm{DC=5}\,\)から
　\(\hspace{10pt}\displaystyle \mathrm{CF}=\color{magenta}{\frac{1}{2}}\,,\,\mathrm{KF}=\color{magenta}{2}\)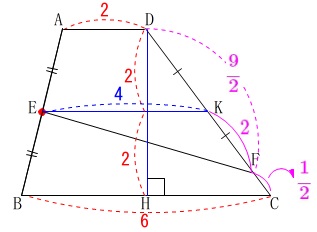このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{KF:FC}&=&2:\frac{1}{2}\\
&=&\color{blue}{4}:\color{blue}{1}
\end{eqnarray}\)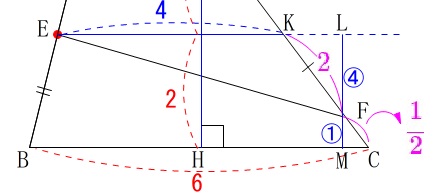このとき\(\,\mathrm{△EKF}\,\)の面積\(\,S_2\,\)は
　\(\begin{eqnarray}\displaystyle
S_2&=&\frac{1}{2}\times \color{blue}{4}\times \color{red}{2}\times \frac{4}{5}\\
&=&\frac{16}{5}
\end{eqnarray}\)

よって、求める四角形\(\,\mathrm{EBCF}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&S_1-S_2\\
&=&10-\frac{16}{5}\\
&=&\underline{　\frac{34}{5}　\mathrm{cm^2}}
\end{eqnarray}\)
　
台形\(\,\mathrm{ABCD}\,\)から引いても良いですよ。

それよりも\(\,\color{red}{★}\,\)を当たり前のように使ってしまいましたが、
一般向けに説明しておきます。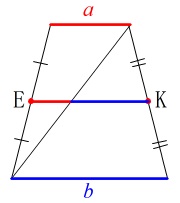台形の脚の中点どうしを結ぶと、
上底の半分と下底の半分を加えたものになります。
　\(\displaystyle \mathrm{EK}=\frac{\color{red}{a}+\color{blue}{b}}{2}\)

他の部分は自分で手を動かして確認してください。
愛知県の問題は時間が十分とは言えないので手を止めたら終わりますよ。

(3)
2つの円の面積の和と円錐台の体積を求めます。
どちらも長さが与えられていて具体的に進めることができます。

条件
問題にある展開図において、
　\(\,\mathrm{DA=CB=3}\,\)
　\(\,\mathrm{ \stackrel{\large{\frown}}{\mbox{AB}}}=6\,\pi\,\)
　\(\,\mathrm{ \stackrel{\large{\frown}}{\mbox{DC}}}=4\,\pi\,\)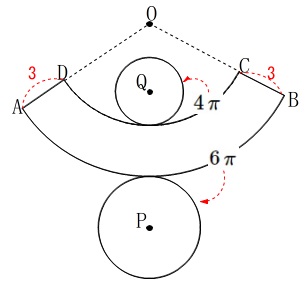
ここで円\(\,\mathrm{P,Q}\,\)の周が\(\,6\,\pi\,,\,4\,\pi\,\)になることが分からない人は『覚え太郎』からやり直してください。

①
円\(\,\mathrm{P}\,\)と円\(\,\mathrm{Q}\,\)の面積の和です。

周の長さが分かっているので半径が分かります。

　円\(\,\mathrm{P}\,\)の半径：\(\,\color{red}{3}\,\)
　円\(\,\mathrm{Q}\,\)の半径：\(\,\color{blue}{2}\,\)

よって、求める面積\(\,S\,\)は、
　\(\begin{eqnarray}
S&=&\pi\times \color{red}{3}^2+\pi\times \color{blue}{2}^2\\
&=&9\,\pi+4\,\pi\\
&=&\underline{　13\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)

②
半径が分かった時点で見取り図も書いておけば良かったのですが、
問題の順序に合わせました。
※
本来なら条件を読み取った時点で見取り図は書いておくといいです。
その時点で①はほぼ終わっています。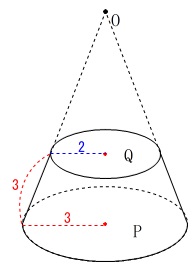円錐台の体積を求める公式はありますが、
相似を利用して具体的に体積を求めておきます。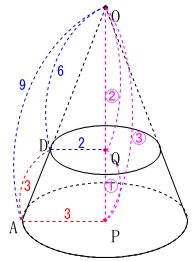2つの底面となる円の中心を\(\,\mathrm{Q,P}\,\)とすると、
小さい円錐と大きい円錐の相似比は
　\(\hspace{10pt}\mathrm{DQ:AP}=\color{red}{3}:\color{blue}{2}\)
なので
　\(\,\mathrm{OD=6}\,\)
　\(\,\mathrm{OA=9}\,\)

三平方の定理から高さとなる\(\,\mathrm{OQ}\,\)は、
　\(\begin{eqnarray}
\mathrm{OQ}&=&\sqrt{6^2-2^2}\\
&=&\sqrt{32}\\
&=&4\sqrt{2}
\end{eqnarray}\)

これから\(\,\mathrm{OQ}\,\)を高さとする小さい円錐の体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times 4\,\pi\times 4\sqrt{2}\\
&=&\frac{16\sqrt{2}}{3}\,\pi
\end{eqnarray}\)

また
　\(\begin{eqnarray}
\mathrm{OP}&=&\sqrt{9^2-3^2}\\
&=&\sqrt{72}\\
&=&6\sqrt{2}
\end{eqnarray}\)
（三平方の定理ではなく、相似比からでも良いです。）

これから\(\,\mathrm{OP}\,\)を高さとする大きい円錐の体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times 9\,\pi\times 6\sqrt{2}\\
&=&18\sqrt{2}\,\pi
\end{eqnarray}\)

よって、求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&V_2-V_1\\
&=&18\sqrt{2}\,\pi-\frac{16\sqrt{2}}{3}\,\pi\\
&=&\frac{54\sqrt{2}-16\sqrt{2}}{3}\,\pi\\
&=&\underline{　\frac{38\sqrt{2}}{3}\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

相似比を体積比にまで利用すると、
大きい円錐と小さい円錐の相似比が\(\,3:2\,\)なので
体積比は
　\(3^3:2^3=27:8\)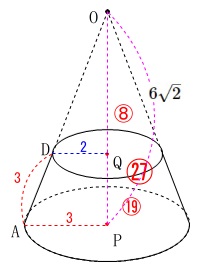
大きい円錐（全体）と円錐台（上の円錐を取り除いた立体）の体積比は
　\(27:(27-8)=27:19\)

これから
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 9\,\pi\times 6\sqrt{2}\times \frac{19}{27}\\
&=&\frac{38\sqrt{2}}{3}\,\pi　\mathrm{cm^3}
\end{eqnarray}\)

または、小さい円錐の高さが先に出たなら
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 4\,\pi\times 4\sqrt{2}\times \frac{19}{8}\\
&=&\frac{38\sqrt{2}}{3}\,\pi　\mathrm{cm^3}
\end{eqnarray}\)

でも同じです。

円錐台の公式を用いると、、、
長くなりましたので省略します。
（この程度で使う必要も無いですが、会員はカードで確認しておいてください。）

\(\,2020\,\)年愛知県\(\,\mathrm{B}\,\)日程の数学は以上です。

あれこれ浮かんで自分でも何を伝えたかったのか分からなくなったところもあります。
勘違いも含めミスもあると思います。笑
お気づきになられた方はご指摘ください。

⇒　2020年愛知県公立高校入試A日程の数学問題の解説

\(\,\mathrm{A}\,\)日程も求めていることは同じです。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

愛知県では\(\,2021\,\)年度は削除項目はありませんので、
今まで通りということですよ。
（問題の難易度はどうするか知りませんけど。）