2020年（令和2年）度に行われた京都府公立高校入試の前期選抜数学の問題と解説です。
今回の規則性は少し楽にはなりましたが、偏り無く全分野からの知識が問われています。
問題の質と量は全国でもトップクラスの公立入試ですので詳しい説明は無しにしてとっとと終わらせます。
2020年京都府公立高校入試前期選抜学力試験の数学問題
\(\,2021\,\)年度の入試では三平方の定理と標本調査は出題範囲から除外されます。
冒頭でも書いた通り、
問題はさらっと\(\,4\,\)ページで大問\(\,6\,\)題でかわいく見えますが、
問題の質と量ともにかわいい問題ではありません。
2020年京都府公立高校入試前期選抜学力試験の数学問題の解説
詳しく説明しているとかなり長くなりそうなのでさらっと済ませます。
第１問小問題集合
\(\,\large{1}\,\)
主に計算問題が\(\,9\,\)問あります。
(1)
符号に注意しながら掛け算が先です。
\(\hspace{10pt}\displaystyle 8\times \left(-\frac{3}{2}\right)^2-(-4^2)\\
\displaystyle =8\times \frac{9}{4}-(-16)\\
=18+16\\
=\underline{ 34 }\)
(2)
分母は1つにして、分子の計算に集中します。
\(\hspace{10pt}\displaystyle \frac{4a-3}{6}-\frac{6a-5}{9}\\
\displaystyle =\frac{3(4a-3)-2(6a-5)}{18}\\
\displaystyle =\frac{12a-9-12a+10}{18}\\
\displaystyle =\underline{ \frac{1}{18} }\)
文字式でも数値計算でも基本的な方法をそろえておくと良いですよ。
(3)
割り算は逆数の掛け算、
これは算数から変わりません。
\(\hspace{10pt}\displaystyle \frac{2}{3}x^2y^3\div \left(-\frac{1}{8}xy\right)\div \frac{4}{9}y\\
\displaystyle =-\frac{2x^2y^3\times 8\times 9}{3\times xy\times 4y}\\
=\underline{ -12xy }\)
\(\,2\,\)行目に逆数の掛け算にしていますが、
分母分子にまわる数値、文字に注意しましょう。
(4)
中心角と面積は比例します。
半径\(\,4\,\)の面積は\(\,16\pi\,\)なので
\(\begin{eqnarray}\displaystyle
16\pi\times \frac{x}{360}&=&6\pi\\
x&=&\frac{6\times 360}{16}\\
&=&\underline{135 ^{\circ}}
\end{eqnarray}\)
会員は「比例計算は時計回り」が常識となっているのでそのまま計算しましたが、
比例計算になれていない人は比例式を立てても良いです。
(5)
方程式を満たす値が方程式の解です。
\( \begin{cases}
\hspace{7pt} 5a+3b=23\\
\hspace{7pt} 10+3a=31
\end{cases}\)
これを解いて
\(\hspace{4pt}\underline{ a=7\,,\,b=-4 }\)
(6)
これは説明するまでもないでしょう。
条件式の無理数を残して平方します。
\(\begin{eqnarray}
a&=&\sqrt{30}-6\\
a+6&=&\sqrt{30}\\
(a+6)^2&=&30\\
a^2+12a+36&=&30
\end{eqnarray}\)
ここからは好きにしていいです。
\(\hspace{4pt}\color{red}{a^2+12a}=-6\)
として、
\(\hspace{10pt}\color{red}{a^2+12a}+35\\
=\color{red}{-6}+35\\
=\underline{ 29 }\)
直接代入しても大した計算ではありませんが数学しましょう。
過去問解説は別枠にしておきたいところですが、
説明すると分かっている人にはムダが多くなるのでリンクさせておきます。
(7)
因数分解できないので解の公式です。
\(\begin{eqnarray}\displaystyle
x&=&\frac{8\pm \sqrt{(-8)^2-4\times 3\times (-4)}}{2\times 3}\\
&=&\frac{8\pm\sqrt{64+48}}{6}\\
&=&\frac{8\pm 4\sqrt{7}}{6}\\
&=&\underline{ \frac{4\pm 2\sqrt{7}}{3} }
\end{eqnarray}\)
たぶん、\(\,x\,\)の係数が偶数なので
\(\begin{eqnarray}\displaystyle
x&=&\frac{4\pm \sqrt{4^2-3\times (-4)}}{3}\\
&=&\frac{4\pm \sqrt{16+12}}{3}\\
&=&\underline{ \frac{4\pm 2\sqrt{7}}{3} }
\end{eqnarray}\)
とした人もいるでしょう。
(8)
\(\,y\,\)軸より左で増加している関数を選びます。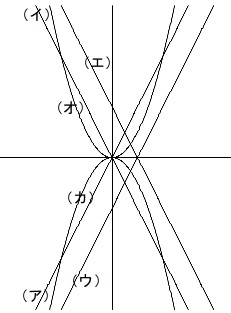
答え \(\,\underline{ (ア) (ウ) (カ) }\,\)
(9)
少なくとも\(\,\mathrm{1}\,\)個黒玉が残る確率です。
黒玉が\(\,\mathrm{2}\,\)個残るか、\(\,\mathrm{1}\,\)個残るかのどちらかですが、
逆に考えれば黒玉が残らない場合を見れば早いです。
普通に考えます。
白玉\(\,(\color{red}{1},\color{red}{2},\color{red}{3},\color{red}{4})\,\)と黒玉\(\,(5,6)\,\)をすべて区別して考えると、
\(\,2\,\)個の取り出し方は、
\(\,1\,\)回目が\(\,6\,\)通り
\(\,2\,\)回目は1つ減って\(\,5\,\)通り
あるので、
\(\hspace{4pt}6\times 5=30\,\)通り。
樹形図が楽です。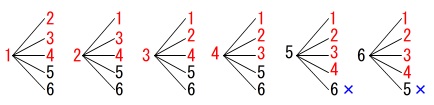
2つ連続で黒玉を取り出すと黒は残らないので、
少なくとも\(\,1\,\)個は黒玉が残る確率は
\(\hspace{4pt}\displaystyle \frac{28}{30}=\underline{ \frac{14}{15} }\)
黒が残らない確率は
\(\displaystyle \frac{2}{30}=\frac{1}{15}\)
なので求める確率は
\(\hspace{10pt}\displaystyle 1-\frac{1}{15}\\
\displaystyle =\underline{ \frac{14}{15} }\)
としも良いです。
白玉、黒玉を区別するのは基本ですが、
確率の積を利用できるなら必要ありません。
一つ目黒である確率は
\(\hspace{4pt}\displaystyle \frac{2}{6}\)
二つ目は1つ減っているので二つ目も黒である確率は
\(\hspace{4pt}\displaystyle \frac{1}{5}\)
よって、\(\,2\,\)回とも黒である確率は
\(\hspace{4pt}\displaystyle \frac{2}{6}\times \frac{1}{5}=\frac{1}{15}\)
確率はすべてを加えると\(\,1\,\)になるので、
「\(\,2\,\)回とも黒」ではない確率は
\(\hspace{10pt}\displaystyle 1-\frac{1}{15}\\
\displaystyle =\underline{ \frac{14}{15} }\)
余事象といいますが簡単にいえば「起こらない確率」です。
第２問データの活用
\(\,\large{2}\,\)
データの活用の中央値と度数を求める問題です。
(1)
\(\,1\,\)年生\(\,50\,\)人の中央値を度数分布表から考えます。
\(\,50\,\)人なので小さい順に（累積度数）を見て、
\(\,25\,\)番目と\(\,26\,\)番目の人の冊数の平均
となるので
\(\,6\,\)冊以上\(\,8\,\)冊未満の階級
ということが分かります。
ただし、この階級には\(\,8\,\)冊の人はいません。
（冊数は整数なので\(\,8\,\)冊は次の階級に含まれます。）
よって、\(\,25\,\)番目と\(\,26\,\)番目の人の冊数は
\(\,6\,\)冊と\(\,6\,\)冊
\(\,6\,\)冊と\(\,7\,\)冊
\(\,7\,\)冊と\(\,7\,\)冊
とのどれかです。
このことから考えられる中央値は
\(\,6\,,\,6.5\,,\,7 (冊)\,\)
のどれかになります。
答え \(\,\underline{ （ア） （イ） （ウ） }\,\)
(2)
条件から\(\,3\,\)年生の度数を求めます。
条件
①\(\,4\,\)冊以上\(\,6\,\)冊未満の相対度数は\(\,1\,\)年生と等しい。
②\(\,8\,\)冊以上\(\,10\,\)冊未満の階級の相対度数は\(\,3\,\)年生の方が大きい。
③\(\,3\,\)年生の最大値は\(\,16\,\)冊であった。
条件①から\(\,4\,\)冊以上\(\,6\,\)冊未満の\(\,1\,\)年生の相対度数は
\(\hspace{4pt}\displaystyle \frac{10}{50}=\color{red}{0.2}\)
なので\(\,3\,\)年生の度数は、
\(\hspace{10pt}\mathrm{X}=40\times \color{red}{0.2}=\underline{ 8 }\)
もちろん、
\(\hspace{4pt}\displaystyle \frac{\mathrm{X}}{40}=\color{red}{0.2}\)
を解いても良いです。
\(\,\mathrm{X=8}\,\)と分かれば他の階級の度数から
\(\hspace{4pt}\mathrm{Y+Z}=14\)
とまでは分かります。
条件②から\(\,8\,\)冊以上\(\,10\,\)冊未満の階級の相対度数は\(\,3\,\)年生の方が大きいので
\(\hspace{4pt}\displaystyle \frac{15}{50}＜\frac{\mathrm{Y}}{40}\)
なので
\(\hspace{4pt}12＜\mathrm{Y}\)
具体的にいえば\(\,\mathrm{Y}\,\)には\(\,13\,\)か\(\,14\,\)が入ります。
ここで、条件③から\(\,16\,\)冊以上\(\,18\,\)冊未満の階級には、
\(\,16\,\)冊の人が少なくとも\(\,1\,\)人はいるので、
\(\hspace{10pt}\mathrm{Y}=\underline{ 13 }\)
しかありません。
（\(\,\mathrm{Y}=14\,\)だと\(\,\mathrm{Z}=0\,\)となり最大値が合わない。）
このとき、\(\,\mathrm{Z}=\underline{ 1 }\,\)
答え \(\underline{ \mathrm{X}=8\,,\,\mathrm{Y}=13\,,\,\mathrm{Z}=1 }\)
\(\,\large{1}\,\)の計算の後なので気が抜けるかもしれませんが、
ここで気を抜いてはいけません。
第３問円と円周角
\(\,\large{3}\,\)
円に内接する四角形があります。
\(\,\mathrm{AD=DC=12}\,\)
\(\,\mathrm{DE=9}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。）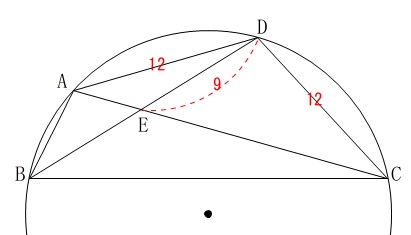
円に内接している条件が分かれば中心より下の半円は見なくて良いのでカットしています。
(1)
\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△EAD}\,\)を証明します。
同一（または同一長）の弧に対する円周角は等しく、
二等辺三角形の底角も等しいので、
図の同じ印は等しい角になります。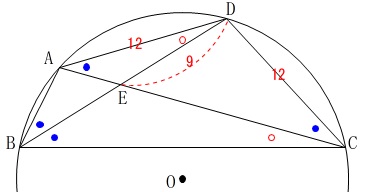
他にも等しい角はありますが証明は終わっていますね。
\(\,2\,\)角相等により
\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△EAD}\,\)
証明は適当にやっておいてください。
\(\,①\,\)円周角が等しい。
\(\,②\,\)二等辺三角形の底角が等しい。
という条件と共通角から
\(\,2\,\)組の角がそれぞれ等しい。
という『相似条件』が書かれていれば減点されるところはありません。
(2)
(1)で誘導してくれているので相似を使いましょう。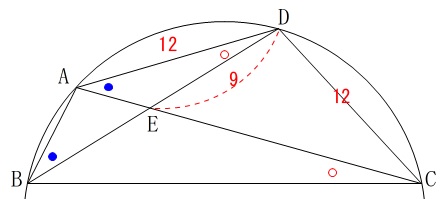
\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△EAD}\,\)
なので、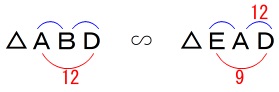
\(\begin{eqnarray}\displaystyle
\mathrm{AD:ED}&=&\mathrm{BD:AD}\\
12:9&=&\mathrm{BD}:12\\
9\times \mathrm{BD}&=&12\times 12\\
\mathrm{BD}&=&16
\end{eqnarray}\)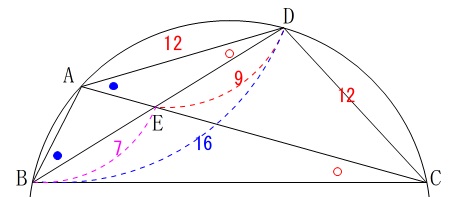
このことから
\(\begin{eqnarray}
\mathrm{BE}&=&\mathrm{BD-ED}\\
&=&\color{blue}{16}-\color{red}{9}\\
&=&\underline{ 7 \mathrm{cm}}
\end{eqnarray}\)
(3)
線分\(\,\mathrm{AC}\,\)の長さと\(\,\mathrm{△ABC}\,\)の面積を求めます。
具体的な角度が与えられますが、角度の問題ではありません。
\(\,\mathrm{∠ACD=30^{\circ}}\,\)の意味を考えれば長さに直結します。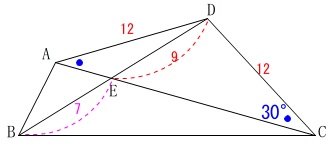
頂点\(\,\mathrm{D}\,\)から\(\,\mathrm{AC}\,\)に垂線\(\,\mathrm{DM}\,\)を下ろすと、
\(\,\mathrm{DM}\,\)は「二等辺三角形の頂角の二等分線」で、
合同な三角定規が2つできます。
辺の比は
\(\,\mathrm{DM:DC:MC=1:2:\sqrt{3}}\,\)
なので、
\(\,\mathrm{DM=\color{blue}{6}\,,\,MC=\color{blue}{6\sqrt{3}}}\,\)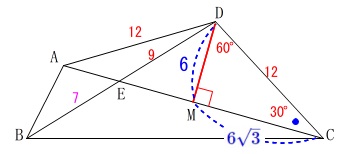
\(\,\mathrm{△DAM≡△DCM}\,\)なので、
線分\(\,\mathrm{AC}\,\)は
\(\begin{eqnarray}
\mathrm{AC}&=&\mathrm{MC}\times 2\\
&=&6\sqrt{3}\times 2\\
&=&\underline{ 12\sqrt{3} \mathrm{cm}}
\end{eqnarray}\)
また、\(\,\mathrm{△ABC}\,\)の面積は\(\,\mathrm{B}\,\)から直線\(\,\mathrm{AC}\,\)に垂線\(\,\mathrm{\color{magenta}{BN}}\,\)を引くと、
\(\,\mathrm{\color{magenta}{△EBN}}\,\)∽\(\,\mathrm{\color{blue}{△EDM}}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{BN:DM}&=&\mathrm{BE:DE}\\
\mathrm{BN}:\color{blue}{6}&=&\color{magenta}{7}:\color{blue}{9}\\
9\times \mathrm{BN}&=&6\times 7\\
\mathrm{BN}&=&\frac{14}{3}
\end{eqnarray}\)
底辺を\(\,\mathrm{AC}\,\)と見ているので
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AC}\times \mathrm{BN}\\
&=&\frac{1}{2}\times 12\sqrt{3}\times \frac{14}{3}\\
&=&\underline{ 28\sqrt{3} \mathrm{cm^2} }
\end{eqnarray}\)
\(\,\mathrm{BN}\,\)の長さを高さとして具体的に出しましたが、
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{\color{magenta}{7}}{\color{blue}{9}}\times \mathrm{△ADC}\\
&=&\frac{7}{9}\times \frac{1}{2}\times 12\sqrt{3}\times 6\\
&=&\underline{ 28\sqrt{3} \mathrm{cm^2} }
\end{eqnarray}\)
と同じことです。
ちなみに、\(\,\mathrm{DM}\,\)は\(\,\mathrm{AC}\,\)の垂直二等分線なので円の中心を通ります。
そこまで気が回った人は少し惑わされたかもしれませんね。
\(\,\mathrm{BC}\,\)では無く、\(\,\mathrm{AC}\,\)を底辺に見るので、
少し図を回転させて見るとわかりやすい問題でした。
第４問関数
\(\,\large{4}\,\)
関数の問題ですが比例定数を求め、
直線の式と面積を等しくする点を求める普通の問題です。
条件を書き出しておきます。
\(\,\mathrm{A,B}\,\)は\(\,y=ax^2\,\)上の点
\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,6\,\)
点\(\,\mathrm{B,C}\,\)は\(\displaystyle \,y=-\frac{1}{2}x+7\,\)上の点
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,2\,\)
直線\(\,\mathrm{BC}\,\)は\(\,y\,\)軸に平行
\(\,\mathrm{ＡＣ:ＣＤ=5:4}\,\)
(1)
比例定数と点\(\,\mathrm{A}\,\)の座標を求めます。
\(\,\mathrm{B}\,\)は\(\displaystyle \,y=-\frac{1}{2}x+7\,\)上の点で、
\(\,x\,\)座標が\(\,6\,\)なので
\(\begin{eqnarray}\displaystyle
y&=&-\frac{1}{2}\times 6+7\\
&=&4
\end{eqnarray}\)
これから\(\,\mathrm{B}\,\)の座標は
\(\hspace{10pt}\mathrm{B}\,(\,6\,,\,4\,)\)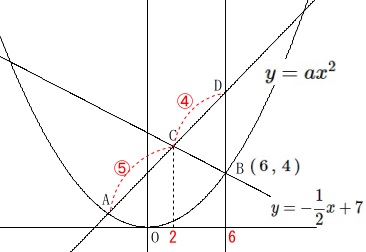
関数\(\,y=ax^2\,\)は\(\,\mathrm{B}\,\)を通るので
\(\begin{eqnarray}\displaystyle
4&=&a\times (6)^2\\
a&=&\underline{ \frac{1}{9} }
\end{eqnarray}\)
このとき
\(\hspace{10pt}\displaystyle y=\frac{1}{9}\,x^2\)
また\(\,\mathrm{ＡＣ:ＣＤ=5:4}\,\)なので、
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,x\,\)座標の差の比を考えて
\(\begin{eqnarray}
(2-x):(6-2)&=&5:4\\
x&=&\underline{ -3 }
\end{eqnarray}\)
Aの座標を出しておきます。
\(\,\mathrm{A}\,\)の\(\,y\,\)座標は
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{9}\,(-3)^2\\
&=&1
\end{eqnarray}\)
より、
\(\,\mathrm{A\,(\,-3\,,\,1\,)}\,\)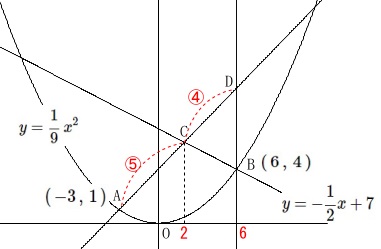
本来なら次の(2)および点\(\,\mathrm{D}\,\)の座標を出すまでは問題に無くてもやっておいた方が良いです。
(2)
直線\(\,\mathrm{AC}\,\)の式を求めます。
\(\,\mathrm{C}\,\)の座標が必要ですが、
直線\(\,\mathrm{BC}\,\)を通り\(\,x\,\)座標が\(\,2\,\)なので、
\(\,\mathrm{C}\,\)の\(\,y\,\)座標は
\(\begin{eqnarray}\displaystyle
y&=&-\frac{1}{2}\,(2)+7\\
&=&6
\end{eqnarray}\)
だから
\(\hspace{4pt}\mathrm{C}\,(\,2\,,\,6\,)\)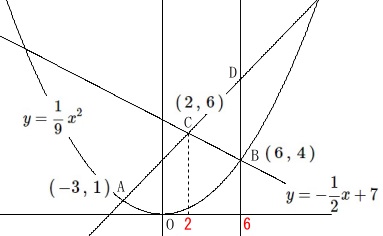
よって、直線\(\,\mathrm{AC}\,\)は\(\,2\,\)点
\(\hspace{4pt}\mathrm{A}\,(\,-3\,,\,1\,)\)
\(\hspace{4pt}\mathrm{C}\,(\,2\,,\,6\,)\)
を通るので
\(\hspace{10pt}\underline{ y=x+4 }\)
傾きから求める方法で良いですよ。
(3)
直線\(\,\mathrm{AC}\,\)上にある四角形\(\,\mathrm{OBCA}\,\)と\(\,\mathrm{△OEA}\,\)が等しくなる点\(\,\mathrm{E}\,\)を求めます。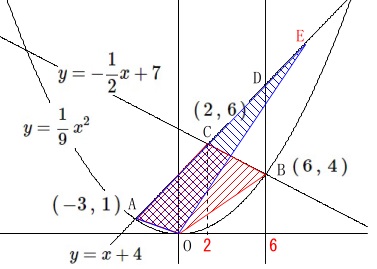
\(\,\mathrm{A}\,\)より左にも面積が等しくなる点はありますが、
\(\,\mathrm{E}\,\)の\(\,x\,\)座標は正なので1つです。
具体的な面積が求まるので計算しても良いのですが、
等積移動させたい問題なので平行線を利用します。
四角形\(\,\mathrm{OBCA}\,\)と\(\,\mathrm{△OEA}\,\)は\(\,\mathrm{\color{magenta}{△OAC}}\,\)を共通にしています。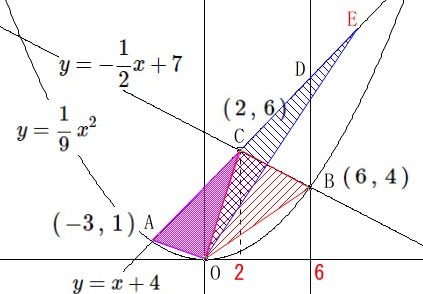
このことから
\(\,\mathrm{\color{red}{△OBC}}\,\)と\(\,\mathrm{\color{blue}{△OCE}}\,\)
の面積が等しくなれば良いことになります。
線分\(\,\mathrm{OC}\,\)を共通の底辺とみると、
高さが平行移動しても面積は等しいので、
\(\,\mathrm{△OBC=△OCE}\,\)
となります。
つまり、
\(\,\mathrm{B}\,\)を通り直線\(\,\mathrm{OC}\,\)に平行な直線と、
直線\(\,\mathrm{AC}\,\)との交点が\(\,\mathrm{E}\,\)
です。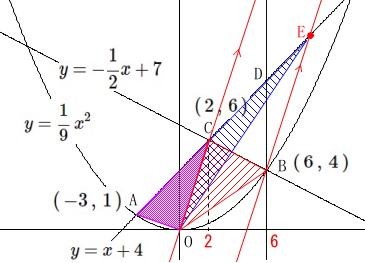
直線\(\,\mathrm{OC}\,\)は比例の関数で
\(\hspace{10pt}y=3x\)
この直線に平行で点\(\,\mathrm{B}\,\)を通る直線は
\(\hspace{4pt}\mathrm{B}\,(\,6\,,\,4\,)\)
なので
\(\hspace{10pt}y=3x-14\)
直線\(\,\mathrm{AC}\,\)は\(\,y=x+4\,\)なので交点\(\,\mathrm{E}\,\)は
\(\hspace{10pt}\mathrm{E}\,\underline{ (\,9\,,\,13\,) }\)
会員は点\(\,\mathrm{E}\,\)を\(\,(\,t\,,\,t+4\,)\,\)おいて、
面積計算したくなるかもしれませんが、
簡単に終わるので自分でやっておいてください。
（四角形\(\,\mathrm{OBCA}\,\)の面積は\(\,24\,\)です。）
第５問立体と断面
\(\,\large{5}\,\)
条件を整理した結果からいうと、直方体を平面で切る問題です。
条件を書き出しておきます。
\(\,\mathrm{ABCD-EFGH}\,\)は直方体
\(\,\mathrm{AB=AD=6}\,\)
\(\,\mathrm{AE=12}\,\)
\(\,\mathrm{BP=DQ=3}\,\)
\(\,\mathrm{CQ}\,\)∥\(\,\mathrm{PR}\,\)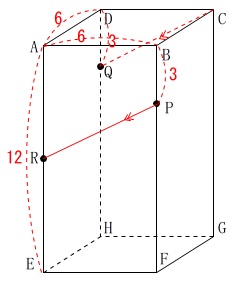
対面で平行なので\(\,\mathrm{C,P,R,Q}\,\)は同一平面上にあります。
さらに\(\,4\,\)辺の長さも等しいのでひし形です。
(1)
\(\,\mathrm{PQ}\,\)の長さは\(\,\mathrm{BD}\,\)の長さに等しいので
\(\begin{eqnarray}
\mathrm{PQ}&=&\mathrm{BD}\\
&=&\underline{ 6\sqrt{2} \mathrm{cm}}
\end{eqnarray}\)
(2)
四角形\(\,\mathrm{CQRP}\,\)、ひし形の面積です。
問題にある長さの条件から
\(\begin{eqnarray}
\mathrm{CR}&=&\sqrt{6^2+6^2+6^2}\\
&=&6\sqrt{3}
\end{eqnarray}\)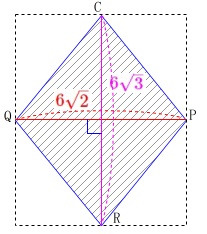
よって、四角形\(\,\mathrm{CQRP}\,\)の面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times \mathrm{CR}\times \mathrm{PQ}\\
&=&\frac{1}{2}\times 6\sqrt{2}\times 6\sqrt{3}\\
&=&\underline{ 18\sqrt{6} \mathrm{cm^2}}
\end{eqnarray}\)
また、直線\(\,\mathrm{CQ}\,\)と直線\(\,\mathrm{PR}\,\)の距離\(\,\color{red}{d}\,\)は、
四角形\(\,\mathrm{CQRP}\,\)の底辺を\(\,\mathrm{CQ}\,\)と見たときの高さになります。
ここで\(\,\mathrm{CQ}\,\)は直方体の\(\,\mathrm{△QDC}\,\)から
\(\begin{eqnarray}
\mathrm{CQ}&=&\sqrt{3^2+6^2}\\
&=&\sqrt{45}\\
&=&3\sqrt{5}
\end{eqnarray}\)
四角形\(\,\mathrm{CQRP}\,\)の面積は変わらないので、
\(\begin{eqnarray}\displaystyle
3\sqrt{5}\times \color{red}{d}&=&18\sqrt{6}\\
\color{red}{d}&=&\frac{18\sqrt{6}}{3\sqrt{5}}\\
&=&\underline{ \frac{6\sqrt{30}}{5} \mathrm{cm}}
\end{eqnarray}\)
(3)
条件が加わります。
線分\(\,\mathrm{AF}\,\)と線分\(\,\mathrm{PR}\,\)の交点を\(\,\mathrm{S}\,\)
\(\,\mathrm{SF}\,\)の中点を\(\,\mathrm{M}\,\)
このとき三角錐\(\,\mathrm{MCQP}\,\)の体積を求めます。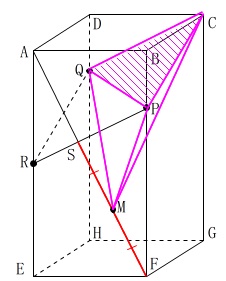
底面を\(\,\mathrm{△CPQ}\,\)と見ても高さは具体的ではありません。
ちょっと見方を変えると、求める三角錐の体積は、
三角錐\(\,\mathrm{F-CPQ}\,\)の半分です。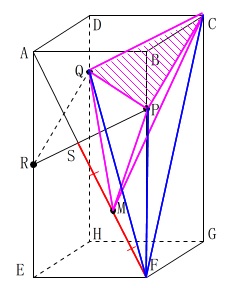
これは少し説明が必要でしょう。
\(\,\mathrm{S}\,\)は底面と見なした平面\(\,\mathrm{CPRQ}\,\)上にあります。
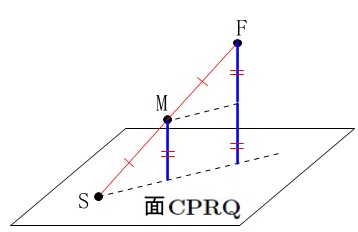
\(\,\mathrm{SF}\,\)の中点が\(\,\mathrm{M}\,\)なので、
\(\,\mathrm{M}\,\)から平面までの距離が三角錐の高さになりますが、
\(\,\mathrm{F}\,\)から平面までの距離の半分です。
（平面のどこに下りるかは関係ありません。）
ところで、
三角錐\(\,\mathrm{Q-CPF}\,\)は底面を\(\,\mathrm{△CPF}\,\)と見て高さが\(\,\mathrm{QT}\,\)です。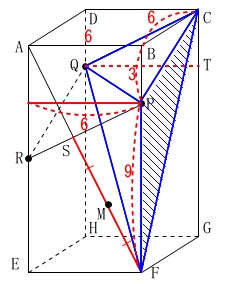
\(\,\mathrm{QT}\,\)の長さは\(\,\mathrm{AB}\,\)に等しいので、
三角錐\(\,\mathrm{Q-CPF}\,\)の体積\(\,V_1\,\)は
\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \mathrm{△CPF}\times \mathrm{QT}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 9\times 6\times 6\\
&=&54
\end{eqnarray}\)
求める三角錐\(\,\mathrm{MCQP}\,\)の体積\(\,V\,\)はその半分で
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{2}\times V_1\\
&=&\underline{ 27 \mathrm{cm^2}}
\end{eqnarray}\)
他にも、
底面となる面がひし形の半分であることから、
三角錐\(\,\mathrm{F-CPR}\,\)を求めに行くなど、
求め方はいくらでもあります。
一番きついのは底面を\(\,\mathrm{△CQP}\,\)とみて、
そのまま高さを求めに行く方法でしょう。
第６問約数と規則性
\(\,\large{6}\,\)
約数と規則性の問題です。
〈規則〉があるので読み取っておきましょう。
・\(\,n\,\)は\(\,1\,\)から始まる自然数
・\(\,n\,\)回目には\(\,n\,\)の約数のうち\(\,9\,\)以下の約数の箱に玉を\(\,1\,\)個ずつ入れる
いくつか例えがあるのでおおよそ規則はつかめると思いますが、
\(\,10\,\)以上の約数は関係ないので、
箱に入る数は\(\,1\,\)から\(\,9\,\)までの倍数の数だけ見ておけば良いことに注意しましょう。
(1)
\(\color{black}{\fbox{6}}\)の箱に玉を入れるのは\(\,n\,\)が\(\,6\,\)の倍数のときだけなので、
\(\,3\,\)個目の玉を\(\color{black}{\fbox{6}}\)の箱に入れるのは
\(\,n=6\times 3\,=18\,\)
つまり、\(\,18\,\)回目の操作ではじめて\(\,3\,\)個になります。
同じように
\(n=6\times 4\,=24\)
つまり、\(\,24\,\)回目の操作ではじめて\(\,4\,\)個になります。
答え \(\color{black}{\fbox{ ア }}\) \(\,\underline{ 18 }\,\) \(\color{black}{\fbox{ イ }}\) \(\,\underline{ 24 }\,\)
(2)
(1)で具体的に求めているので規則性は分かります。
\(\color{black}{\fbox{3}}\)の箱にはじめて\(\,b\,\)個の玉が入るのは\(\,n=3b\,\)のとき
なので
\(\hspace{4pt}a=3b ･･･①\,\)
この\(\,85\,\)回後、
\(\,n=3b+85\,\)
の操作ではじめて\(\color{black}{\fbox{8}}\)の箱に\(\,b\,\)個の玉が入ります。
\(\color{black}{\fbox{8}}\)の箱にはじめて\(\,b\,\)個の玉が入るのは\(\,n=8b\,\)のとき
なので
\(\hspace{4pt}3b+85=8b ･･･②\)
①②から
\(\hspace{10pt}\underline{ a=51\,,\,b=17 }\)
(3)
(1)(2)から分かるように、
操作の回数\(\,n\,\)までに倍数が何回出てくるかで箱の玉の数が決まります。
\(\,267\,\)回目から赤玉の代わりに黄玉を入れていきます。
\(\,266\,\)回目までに
\(\,266\,=4\times 66+2\,\)
\(\,266\,=9\times 29+5\)
なので
\(\,4\,\)の倍数は\(\,66\,\)回
\(\,9\,\)の倍数は\(\,29\,\)回
出てくるので
\(\color{black}{\fbox{4}}\)の箱に赤玉は\(\,66\,\)個
\(\color{black}{\fbox{9}}\)の箱に赤玉は\(\,29\,\)個
入っています。
この後\(\color{black}{\fbox{9}}\)の箱に黄玉が、
\(\color{black}{\fbox{4}}\)の箱にある赤玉の数\(\,66\,\)個入るのは、
\(\color{black}{\fbox{9}}\)の箱に赤玉黄玉の合計で
\(\hspace{4pt}29+66\,=95\)個
になったときで、
\(\begin{eqnarray}
n&=&9\times 95\\
&=&855
\end{eqnarray}\)
つまり\(\,855\,\)回の操作で条件を満たします。
このとき\(\,4\,\)の倍数は
\(\,855=4\times 213+3\)
だから\(\,213\,\)回出て来るので、
\(\color{black}{\fbox{4}}\)の箱には\(\,213\,\)個の玉が入っています。
このうち\(\,66\,\)個は赤玉なので黄玉は
\(\hspace{10pt}213-66\\
=\underline{ 147 個}\)
以上です。
条件の読み取りさえできれば\(\,\mathrm{6}\,\)の規則性がやりやすかったのは良いのですが、
全体的に甘くない質と量であることは間違いありません。
⇒ 2020年中期選抜（公開予定）
\(\,2021\,\)年は三平方の定理が除外されるので、
さらに手を動かさないと糸口が見えない練り込まれた問題になるかもしれないですね。
試験本番でいきなり問題が解けるようになるなんてことはないので対策は十分にしておきましょう。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
