2020年(令和2年)度群馬県公立高校入試【前期】数学の問題と解説

2020年(令和2年)度に行われた群馬県公立高校入試前期の数学の問題と解説です。
式の計算から方程式、図形や関数と幅広く基本が問われます。
前期入試は問題数も少なく軽めの問題が多いので一気にサクッと解説します。
嫌らしい問題はなく基本事項をしっかり抑えておけば気をつけるのはミスだけです。

2020年（令和2年）度群馬県公立高校入試前期選抜の数学の問題

問題は大きく\(\,4\,\)問題です。

⇒　令和2年度群馬県公立高校入試前期選抜の数学の問題

2020年（令和2年）度群馬県公立高校入試前期選抜の数学の解説

計算から関数、図形まで基本問題中心です。
試験時間は十分にありますので焦らず取り組みましょう。

第１問基本小問集合

\(\,1\,\)

数値、文字式計算問題が\(\,12\,\)題あります。

(1)
①から⑥までの計算問題です。

①
　\(\hspace{10pt}-4+\color{red}{(-1)\times 5}\\
=-4\color{red}{-5}\\
=\underline{　-9　}\)

足し算引き算より掛け算割り算が先です。

②
　\(\hspace{10pt}7a\times (-3)\\
=\underline{　-21a　}\)

符号に注意して係数と文字部分を別々に計算すれば、
どんな文字式でも同じです。

③
　\(\hspace{10pt}5(x+2)\color{red}{-2(x+4)}\\
=5x+10\color{red}{-2x-8}\\
=\underline{　3x+2　}\)

\(\,2\,\)行目を暗算しないようにした方がミスは減ります。

④
　\(\hspace{10pt}\displaystyle \frac{x+y}{3}-\frac{x+3y}{6}\\
\displaystyle =\frac{2(x+y)\color{red}{-(x+3y)}}{6}\\
\displaystyle =\frac{2x+2y\color{red}{-x-3y}}{6}\\
\displaystyle =\underline{　\frac{x-y}{6}　}\)

分数計算では通分して分母を1つにして、
分子の計算に集中するとミスは減り、早いです。
\(\,3\,\)行目の展開は③と同様に確実にしましょう。

⑤
　\(\hspace{10pt}8a^2b\color{red}{\div (-2a)^2}\\
\displaystyle =\frac{8a^2b}{\color{red}{(-2a)^2}}\\
\displaystyle =\frac{8a^2b}{4a^2}\\
=\underline{　2b　}\)

割り算は逆数の掛け算です。
会員には言うまでもありませんが、『約分の活用』は数学では当然ですね。
ここではそのまま割れますがもっと大きな計算になると違いが出てきますよ。

⑥
　\(\hspace{10pt}\displaystyle \frac{10}{\sqrt{5}}-\color{blue}{\sqrt{45}}\\
\displaystyle =\frac{10\color{red}{\times \sqrt{5}}}{\sqrt{5}\color{red}{\times \sqrt{5}}}-\color{blue}{3\sqrt{5}}\\
\displaystyle =\frac{10\sqrt{5}}{5}-3\sqrt{5}\\
=2\sqrt{5}-3\sqrt{5}\\
=\underline{　-\sqrt{5}　}\)

有理化をていねいにやりましたが、
\(\,45\,\)の素因数分解は確実にやりましょう。
ここではお任せします。

(2)
　\(\hspace{10pt}2x^2y-4xy^2\\
=\underline{　2xy(x-2y)　}\)

因数分解の第\(\,1\,\)手順は、共通因数の抜き出しです。
この問題はそこで終わりますが、
（かっこ）の中が因数分解できるかどうかの確認はしましょう。

(3)
ひもの残りを文字式で表す問題です。
（単位は\(\,\mathrm{cm}\,\)ですが省略します。）

　長さ\(\,90\,\)のひもがある。
　\(\,1\,\)辺が\(\,a\,\)の正方形を\(\,b\,\)個作る。
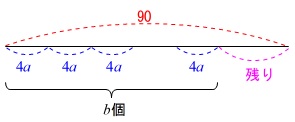正方形は\(\,4\,\)辺あるので1つの正方形で\(\,\color{blue}{4a}\,\)使います。

　\(\hspace{10pt}\color{red}{90}-\color{blue}{4a}\times b\\
=\underline{　90-4ab　}\)

答え　\(\,\underline{　90-4ab　(\,\mathrm{cm}\,)}\)

(4)
反比例の問題です。

「反比例」と見たら先ずは比例定数を求めます。
　\(\hspace{10pt}\displaystyle y=\frac{a}{x}\)

\(\,x=2\,,\,y=-6\,\)を代入して、
　\(\begin{eqnarray}\displaystyle
-6&=&\frac{a}{2}\\
-12&=&a
\end{eqnarray}\)

これでこの問題は終わりです。
　\(\displaystyle \underline{　y=-\frac{12}{x}　}\)

比例定数は
　\(\hspace{10pt}xy=a\)
として求めても良いですよ。

ちなみに、
　比例の関数：\(\,y=\color{red}{a}x\,\)
　反比例の関数：\(\displaystyle \,y=\frac{\color{red}{a}}{x}\,\)
　放物線の関数：\(\,y=\color{red}{a}x^2\,\)
の\(\,\color{red}{a}\,\)はすべて比例定数と呼ぶので忘れないようにしましょう。

(5)
\(\,2\,\)次方程式を解きます。

方程式の基本はすべての項を左辺に集め、
右辺を\(\,0\,\)にすることです。
（\(\,1\,\)次方程式は定数を右辺に集めた方が早い、というだけです。）

　\(\begin{eqnarray}
x(x-2)&=&3\\
x^2-2x-3&=&0\\
(x+1)(x-3)&=&0\\
x&=&\underline{　-1\,,\,3　}
\end{eqnarray}\)

方程式を解くというのは、方程式の解を求めることと同じです。

(6)
直角三角形の斜辺を求めます。

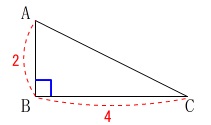
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AC^2}&=&\mathrm{AB^2+BC^2}\\
&=&2^2+4^2\\
&=&4+16\\
&=&20\\
\mathrm{AC}&=&\pm 2\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{AC}\,\)は長さだから\(\,\mathrm{AC\,＞\,0}\,\)なので
　\(\hspace{10pt}\mathrm{AC}=\underline{　2\sqrt{5}　\mathrm{cm}}\)

素因数分解はていねいにしましょう。

(7)
円周角である\(\,\mathrm{∠BDC}\,\)の大きさを求めます。
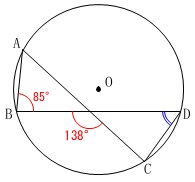分かる角度を一つひとつ書き込めばどうやってもたどり着きます。
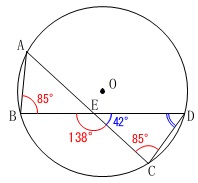円周角が等しいことから
　\(\mathrm{∠ABD=∠ACD}=85^{\circ}\)

三角形の内角の和から
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BDC}&=&180^{\circ}-(\,\mathrm{∠CED+∠ECD}\,)\\
&=&180^{\circ}-(42^{\circ}+85^{\circ})\\
&=&180^{\circ}-127^{\circ}\\
&=&\underline{　53^{\circ}　}
\end{eqnarray}\)
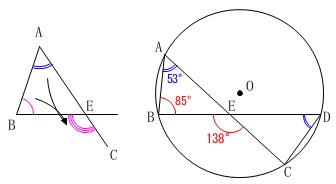三角形の1つの外角は、
他の2つの内角の和になることから、
　\(\begin{eqnarray}
\mathrm{∠BEC}&=&\mathrm{\color{blue}{∠BAE}+∠ABE}\\
\mathrm{\color{blue}{∠BAE}}&=&\mathrm{∠BEC-∠ABE}\\
&=&138^{\circ}-85^{\circ}\\
&=&\color{blue}{53^{\circ}}
\end{eqnarray}\)

これから円周角が等しいことを利用しても同じです。

第２問関数・データ・回転体・確率の小問題集合

\(\,2\,\)

関数のグラフやデータの代表値、
回転体の体積比や確率と\(\,4\,\)問あります。

(1)
5つのグラフから\(\displaystyle \,y=\frac{1}{4}x^2\,\)のグラフを選びます。

放物線のグラフはすべて相似なのですが、
比例定数によって上下および左右の開き具合が変わります。

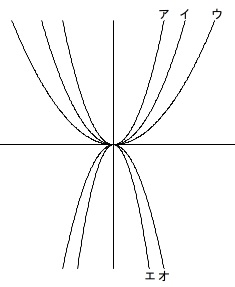
　\(\displaystyle y=\frac{1}{4}x^2\)
は比例定数が正なので上に開きます。
（「下に凸」といいます。）
アイウのどれかになります。

比例定数は小さいほど横に広がった放物線になるので、
　\(\displaystyle y=x^2\,,\,y=\frac{1}{2}x^2\,,\,\frac{1}{4}x^2\)
の中では\(\displaystyle \,y=\frac{1}{4}x^2\,\)が比例定数が小さいから、
ウが\(\displaystyle \,y=\frac{1}{4}x^2\,\)のグラフです。

答え　\(\,\underline{　ウ　}\,\)

問題のグラフには目盛りがあるので
　\((\,4\,,\,4\,)\)
など具体的な関数上の点がどの曲線に乗るかを見ても良いです。

(2)
2つのデータの代表値が等しいといえるものを選びます。

フリースローの成功回数とかはなんでもいいです。
基本通りデータの小さい順に並び替えます。

\(\,1\,\)年生：\(\,8\,\)人
　\(2,3,3,3,5,6,6,8\)
\(\,2\,\)年生：\(\,8\,\)人
　\(3,3,4,4,4,5,6,9\)

ア　中央値

中央値は真ん中の順位になる値なのですが、
データ数が偶数なので真ん中2つの平均が中央値になります。

\(\,1\,\)年生：\(2,3,3,\color{red}{3},\color{red}{5},6,6,8\)
　\(\hspace{10pt}\displaystyle \frac{\color{red}{3}+\color{red}{5}}{2}=4\)
\(\,2\,\)年生：\(3,3,4,\color{blue}{4},\color{blue}{4},5,6,9\)
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{4}+\color{blue}{4}}{2}=4\)

等しいと言える。○

イ　平均値

平均値は総得点を度数合計で割ります。
　\(\displaystyle (\,平均値\,)=\frac{　(\,総得点\,)　}{　(\,度数合計\,)　}\)

度数合計は同じなので総得点だけで比較します。

\(\,1\,\)年生：\(\hspace{10pt}36\)
\(\,2\,\)年生：\(\hspace{10pt}38\)

\(\,2\,\)年生の方が平均値は大きい。×

ウ　最頻値

最頻値は同じ値の度数が一番多い値です。

\(\,1\,\)年生：\(2,\color{red}{3},\color{red}{3},\color{red}{3},5,6,6,8\)
　\(\,\color{red}{3}\,\)が\(\,3\,\)人で最も多いので最頻値\(\,3\,\)
\(\,2\,\)年生：\(3,3,\color{blue}{4},\color{blue}{4},\color{blue}{4},5,6,9\)
　\(\,\color{blue}{4}\,\)が\(\,3\,\)人で最も多いので最頻値\(\,4\,\)

違います。×

エ　範囲

範囲は「(最大値)－(最小値)」のことです。

\(\,1\,\)年生：\(\color{blue}{2},3,3,3,5,6,6,\color{red}{8}\)
　最大値\(\,\color{red}{8}\,\)で最小値\(\,\color{blue}{2}\,\)なので範囲\(\,6\,\)
\(\,2\,\)年生：\(\color{blue}{3},3,4,4,4,5,6,\color{red}{9}\)
　最大値\(\,\color{red}{9}\,\)で最小値\(\,\color{blue}{3}\,\)なので範囲\(\,6\,\)

等しい。○

答え　\(\,\underline{　ア　エ　}\,\)

(3)
回転体の部分的な体積比を求めます。

回転体なので見取り図を書けば分かり易くなります。

条件
　\(\,\mathrm{AB}\,\)の中点が\(\,\mathrm{D}\,\)
　\(\,\mathrm{AC}\,\)の中点が\(\,\mathrm{E}\,\)
　\(\,\mathrm{AC}\,\)を軸として回転させる。
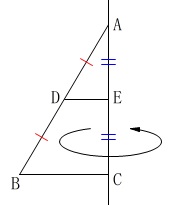回転体は円すいになります。
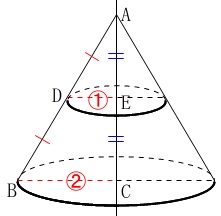高さ\(\,\mathrm{AE}\,\)の円すいと高さ\(\,\mathrm{AC}\,\)の円すいは相似で
　相似比\(\,1:2\,\)
なので
　体積比\(\,1^3:2^3=1:8\,\)
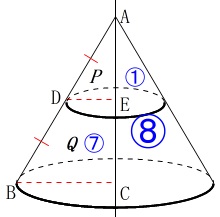全体が\(\,\color{blue}{⑧}\,\)のとき上の円すい\(\,P\,\)は\(\,\color{blue}{①}\,\)なので、
下の円すい台\(\,Q\,\)は全体から上の円すい\(\,P\,\)を引いて\(\,\color{blue}{⑦}\,\)になります。

よって、
　\(\hspace{10pt}P:Q=\underline{　1:7　}\)

(4)
取り出したカードの積が素数になる確率です。

袋の中のカードは
　\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)\(\color{black}{\fbox{3}}\)\(\color{black}{\fbox{4}}\)\(\color{black}{\fbox{5}}\)
がそれぞれ１枚ずつの５枚あります。

\(\,1\,\)回取り出した後、元の袋にもどします。
\(\,2\,\)回目もこの袋から取り出します。

\(\,1\,\)回目にとり出した数字と、
\(\,2\,\)回目にとり出したの数字の積が素数となる確率です。

樹形図で良いです。
ここでは表にします。
　\(\,1\,\)回目取り出した数字を縦
　\(\,2\,\)回目取り出した数字を横
とすると中の数字が\(\,2\,\)数の積です。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \,\color{blue}{1}\, & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5}\\ \hline
\color{red}{1} & 1 & \color{magenta}{2} & \color{magenta}{3} & 4 & \color{magenta}{5}\\ \hline
\color{red}{2} & \color{magenta}{2} & 4 & 6 & 8 & 10\\ \hline
\color{red}{3} & \color{magenta}{3} & 6 & 9 & 12 & 15\\ \hline
\color{red}{4} & 4 & 8 & 12 & 16 & 20\\ \hline
\color{red}{5} & \color{magenta}{5} & 10 & 15 & 20 & 25\\ \hline
\end{array}\)

答え　\(\displaystyle \underline{　\frac{6}{25}　}\)

\(\,1\,\)は素数ではありません。
気をつけておきましょう。

第３問方程式

\(\,3\,\)

持ち帰り用に販売されたコーヒーが何杯か方程式をたてて求めます。

条件
　コーヒーは\(\,1\,\)杯消費税抜きで\(\,200\,\)円
　持ち帰り用は消費税が\(\,8\,\)％
　店内で飲むと消費税が\(\,10\,\)％
　全部で\(\,300\,\)杯売れた。
　売上合計金額は\(\,65180\,\)円であった。

一気に方程式にしても良いですが、
\(\,1\,\)杯あたりの税込み金額を出しておくと分かり易いです。

持ち帰り用は消費財が\(\,8\,\)％なので
　\(\hspace{10pt}200\times 1.08\\
=216　(円)\)

店内で飲む場合は消費財が\(\,10\,\)％なので
　\(\hspace{10pt}200\times 1.10\\
=220　(円)\)

持ち帰り用の販売されたコーヒーを\(\,x\,\)とすると、
店内で販売されたコーヒーは\(\,(\,300-x\,)\,\)となるので、
売上合計で方程式を立てて解くと
　\(\begin{eqnarray}\displaystyle
216x+220(300-x)&=&65180\\
216x+66000-220x&=&65180\\
220x-216x&=&65180-66000\\
-4x&=&-820\\
x&=&205　(適)
\end{eqnarray}\)

答え　\(\,\underline{　205　杯}\,\)

方程式を立てた後の処理は適当に省いて良いです。

テイクアウトとイートインという軽減税率の問題でした。

第４問平面図形

\(\,4\,\)

平行四辺形の性質を利用する平面図形の問題です。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{EF}\,\)

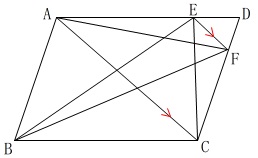
(1)
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△EBC}\,\)の面積が等しいことの証明です。

さりげなく書かれることの多い１番目の条件
　『平行四辺形』
は非常に多くの条件を持っているので見落とさないようにしましょう。
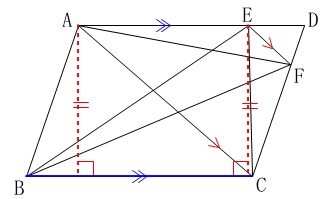平行四辺形の対辺なので
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
だから高さ同じで、底辺\(\,\mathrm{BC}\,\)は共通なので
　\(\,\mathrm{△ABC\,=\,△EBC}\,\)
となります。

答え　\(\,\mathrm{\underline{　ア　AD　イ　BC　}}\,\)
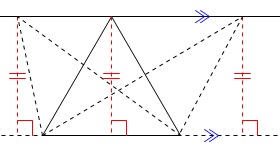三角形の底辺が同じで、
頂点が平行移動したとき底辺までの距離は変わりません。

(2)
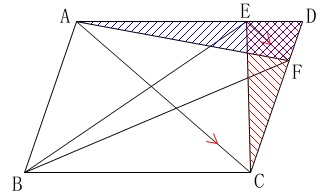
\(\,\mathrm{△ADF}\,\)と\(\,\mathrm{△CDE}\,\)の面積が等しいことを証明します。
(1)で理由を説明してあるので証明だけしておきます。

\(\,\mathrm{△ADF}\,\)と\(\,\mathrm{△CDE}\,\)は
　\(\,\mathrm{△ADF=△AEF+△DEF}\,\)
　\(\,\mathrm{△CDE=△CEF+△DEF}\,\)
と2つの三角形の和になっていて、
　\(\,\mathrm{△DEF}\,\)は共通部分だから面旗は等しい。
また、仮定（条件）から
　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{EF}\,\)
なので
　\(\,\mathrm{△AEF=△CEF}\,\)
である。
よって、
　\(\,\mathrm{△ADF=△CDE}\,\)

(3)
条件が加わります。

条件
　平行四辺形\(\,\mathrm{ABCD}\,\)の面積は\(\,\mathrm{96\,cm^2}\,\)
　\(\,\mathrm{AE:ED=3:1}\,\)
このとき、四角形\(\,\mathrm{EBFD}\,\)の面積を求めます。

　\(\,\mathrm{AC}\,\)∥\(\,\mathrm{EF}\,\)
なので
　\(\,\mathrm{△DEF}\,\)∽\(\,\mathrm{△DAC}\,\)
（これはなくても良いです。）
となり、
　\(\,\mathrm{DF:DC=1:3}\,\)
と分かります。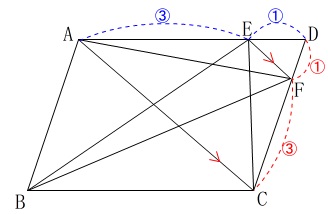ここで、対角線\(\,\mathrm{BD}\,\)で平行四辺形を2つに分けると、

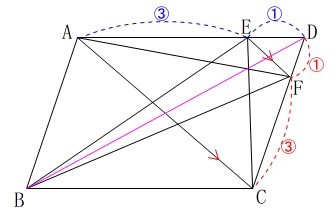
四角形\(\,\mathrm{EBDF}\,\)の面積\(\,S\,\)は
　\(\hspace{10pt}S=\mathrm{\color{blue}{△BED}+\color{red}{△BFD}}\)
となります。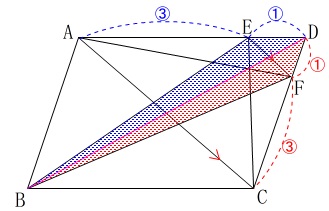　\(\,\mathrm{△ABD}\,\)は平行四辺形\(\,\mathrm{ABCD}\,\)の半分で、
さらに、\(\,\mathrm{AE:ED=3:1}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△AED}&=&\frac{1}{4}\times \mathrm{△ABD}
\end{eqnarray}\)
だから
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△AED}}&=&\frac{1}{4}\times 96\times \frac{1}{2}\\
&=&\color{blue}{12}
\end{eqnarray}\)

同じように
　\(\,\mathrm{\color{red}{△BFD}=\color{red}{12}}\,\)

よって、求める面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{\color{blue}{△AED}+\color{red}{△BFD}}\\
&=&\color{blue}{12}+\color{red}{12}\\
&=&\underline{　24　\mathrm{cm^2}}
\end{eqnarray}\)

(1)(2)から等積移動することも考えられますが、
具体的な面積があるので線分比を利用しました。

以上です。
（こんなにだらだら解説する予定ではなかった。笑）

基本的な問題が多く問題数も多くないので十分満点が狙えます。
推薦される内申点があるなら『覚え太郎』と『基本レポート』で十分ですよ。

⇒　2020年(令和2年)度群馬県公立高校入試【後期】数学の問題と解説

後期選抜でも数学で満点を取って、
差をつけることは十分可能です。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

過去問を見るとわかりますが基本事項の確認と、
普通に数学でやるべきことをやれば解けるように問題は作成されています。