2020年(令和2年)度群馬県公立高校入試【後期】数学の問題と解説

2020年(令和2年)度群馬県で行われた公立高校入試の後期選抜数学の問題と解説です。
全分野から偏りなく出題された、バランスの良い問題です。
群馬県立高校入試では学校によって試験時間が変わるので時間配分に注意は必要ですが、
基本事項を定着させ、問題をよく読めば十分高得点が狙えます。

2020年(令和2年)度群馬県公立高校入試後期選抜数学の問題

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。

⇒　令和2年度群馬県公立高校入試後期選抜数学の問題

※
群馬県の2021年（令和3年）度の学力選抜試験で数学では、
　前期：「三平方の定理」「標本調査」
　後期：「標本調査」
が範囲から除外されます。

後期においては「標本調査」の代わりに「代表値」でも組み込めば、
例年と変わらないということです。

2020年(令和2年)度群馬県公立高校入試後期選抜数学の解説

前期の解説でていねいにやっていますので、
会員向けに近くなりますが、ある程度の計算は解説を省略します。

第１問基本確認の小問集合

\(\,1\,\)
式の計算や方程式、確率、円周角など小問が\(\,11\,\)題あります。

(1)計算問題です。

①
　\(\hspace{10pt}1+2\times (-4)\\
=1-8\\
=\underline{　-7　}\)

計算順序に気をつけましょう。

②
　\(\hspace{10pt}\displaystyle 3x-\frac{1}{2}x\\
\displaystyle =\frac{6x-x}{2}\\
\displaystyle =\underline{　\frac{5x}{2}　}\)

暗算でもできますが、通分が確実です。

答えは\(\,\displaystyle \frac{5}{2}\,x\,\)でも良いです。

③
　\(\hspace{10pt}4a^2b\div2a\times 2b\\
\displaystyle =\frac{4a^2b\times 2b}{2a}\\
=\underline{　4ab^2　}\)

割る（\(\div\)）の直後は分母に回して約分です。

(2)
絶対値が最も大きい数を選びます。

数の大小は数の世界をそろえるのが基本です。
ただ、明らかに大小の分かる小さい方は除外していくと早いです。

ウの\(\,2\sqrt{2}\,\)で
　\(\hspace{4pt}2\sqrt{2}=2\times 1.41\cdots=2.8\cdots\)
と\(\,\sqrt{2}\,\)の近似値を覚えていればすべて小数で比較できます。

答え　\(\,\underline{　イ　}\,\)

近似値を覚えていない場合はルートをつけた数値にそろえることになります。

　\(\hspace{4pt}2\sqrt{2}=\sqrt{8}\)
これと適当な数値を比較すると
　\(\hspace{4pt}|\,-3\,|=\sqrt{9}\)
なので少なくても絶対値は\(\,-3\,\)の方が大きいことが分かります。

(3)
因数分解です。

　\(\hspace{10pt}x^2-10x+25\\
=\underline{　(x-5)^2　}\)

(4)
連立方程式を解きますが、
一文字消去が基本ですね。

　\(\begin{cases}
\hspace{4pt} 2x+3y=4\\
\hspace{4pt} -x+y=3
\end{cases}\)

消去するのはどっちからでもいいです。
ここでは\(\,x\,\)を消去します。

　\(\hspace{22pt}2x+3y=4\\
\underline{+)-2x+2y=6}\\
\hspace{46pt}5y=10\\
\hspace{50pt}y=2\)

これをどれにでも良いですがもどします。
　\(\hspace{4pt}-x+y=3\)
にもどすと
　\(\begin{eqnarray}
-x+(2)&=&3\\
x&=&-1\\
\end{eqnarray}\)

答え　\(\,\underline{　x=-1\,,\,y=2　}\,\)

(5)
硬貨を\(\,3\,\)回投げる確率です。

表を\(\,○\,\)、裏を\(\,×\,\)として樹形図で良いです。

ここでは表にします。
　\(\begin{array}{|c|c|c|} \hline
\,1\,回目\, & \,2\,回目\, & \,3\,回目\, &\,出る\, \\ \hline
○ & ○ & ○ & ● \\ \hline
○ & ○ & × & ● \\ \hline
○ & × & ○ & ● \\ \hline
○ & × & × & ● \\ \hline
× & ○ & ○ & ● \\ \hline
× & ○ & × & ● \\ \hline
× & × & ○ & ● \\ \hline
× & × & × & \\ \hline
\end{array}\)

少なくとも\(\,1\,\)回は表が出る確率は
　\(\hspace{10pt}\displaystyle \underline{　\frac{7}{8}　}\)

「少なくとも」とある場合は普通は逆を考えます。

\(\,1\,\)回も表が出ない確率は
　\(\displaystyle \frac{1}{8}\)
これ以外は\(\,1\,\)回は表が出るので、
確率の全部を合わせると\(\,1\,\)（何かは起こる）、
であることから
　\(\hspace{10pt}\displaystyle 1-\frac{1}{8}=\frac{7}{8}\)
とします。

しかし、ここでは\(\,3\,\)回とも裏という確率を
　\(\hspace{4pt}\displaystyle \frac{1}{2}\times \frac{1}{2}\times \frac{1}{2}=\frac{1}{8}\)
と確率の積で出せないと樹形図や表で出すので変わりないです。

(6)
\(\,2\,\)次方程式を解きます。

方程式を解くときの基本は（左辺）\(\,=0\,\)にすることなので、
　\(\begin{eqnarray}\displaystyle
(2x-5)^2&=&18\\
(2x-5)^2-18&=&0\\
4x^2-20x+25-18&=&0\\
4x^2-20x+7&=&0　･･･①
\end{eqnarray}\)
と変形し解の公式で
　\(\begin{eqnarray}\displaystyle
x&=&\frac{20\pm \sqrt{20^2-4\times 4\times 7}}{2\times 4}\\
&=&\frac{20\pm \sqrt{400-112}}{8}\\
&=&\frac{20\pm \sqrt{288}}{8}\\
&=&\frac{20\pm 12\sqrt{2}}{8}\\
&=&\underline{　\frac{5\pm 3\sqrt{2}}{2}　}
\end{eqnarray}\)
としても良いです。

ただ、ここは左辺を平方の形にしてくれているので
　\(\begin{eqnarray}\displaystyle
(2x-5)^2&=&18\\
2x-5&=&\pm 3\sqrt{2}\\
2x&=&5\pm3\sqrt{2}\\
x&=&\underline{　\frac{5\pm 3\sqrt{2}}{2}　}
\end{eqnarray}\)
と平方根型を利用した方が早いです。

また、
\(\,2\,\)次方程式①の\(\,1\,\)次の項が偶数なので
　\(\begin{eqnarray}\displaystyle
x&=&\frac{10\pm \sqrt{10^2-4\times 7}}{4}\\
&=&\frac{10\pm\sqrt{72}}{4}\\
&=&\frac{10\pm 6\sqrt{2}}{4}\\
&=&\underline{　\frac{5\pm 3\sqrt{2}}{2}　}
\end{eqnarray}\)
と簡略化できますが、それでも平方根型の方が早いです。

(7)
円周角を求めます。

条件は
　\(\,\mathrm{BD}\,\)は円\(\,\mathrm{O}\,\)の直径
　\(\,\mathrm{∠BCD=38^{\circ}}\,\)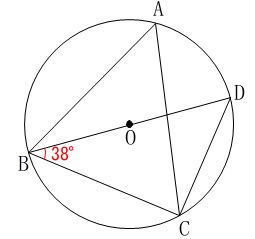直径に対する円周角は\(\,90^{\circ}\,\)なので
　\(\begin{eqnarray}
\mathrm{∠BDC}&=&\color{blue}{52^{\circ}}
\end{eqnarray}\)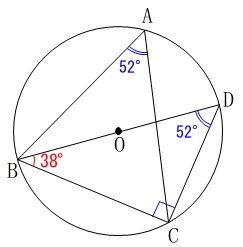
同一の弧\(\,\mathrm{BC}\,\)の円周角は等しいので
　\(\begin{eqnarray}
\mathrm{∠BAC}&=&\mathrm{∠BDC}\\
&=&\underline{　52^{\circ}　}
\end{eqnarray}\)

(8)
標本調査です。
数の分からない黒いビーズの数を推測します。

黒いビーズが\(\,x\,\)個入っている容器に\(\,\color{blue}{100}\,\)個の白いビーズを入れ、
その容器の中から\(\,100\,\)個取り出したら、白いビーズが\(\,10\,\)個入っていた。

白いビーズを容器に入れた後は、
容器全体の白黒ビーズは\(\,x+\color{blue}{100}\,\)になっているので、
　白黒\(\,\color{red}{x+100}\,\)個の中に白いビーズは\(\,\color{blue}{100}\,\)個
　白黒\(\,\color{red}{100}\,\)個の中に白いビーズは\(\,\color{blue}{10}\,\)個
という比例関係が成り立ちます。

比例式で良いです。
　\(\begin{eqnarray}\displaystyle
(x+100):100&=&100:10\\
10(x+100)&=&100\times 100\\
x+100&=&1000\\
x&=&900
\end{eqnarray}\)

答え　\(\,\underline{およそ　900　個}\,\)

「比例計算は時計回り」なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{10}\times \frac{\color{red}{x+100}}{\color{red}{100}}&=&\color{blue}{100}\\
x+100&=&1000\\
x&=&900
\end{eqnarray}\)
でも良いですよ。
※
分数の分母分子が同じ色を表しているなら、
　\(\begin{eqnarray}\displaystyle
\color{blue}{100}\times \frac{\color{red}{100}}{\color{red}{x+100}}&=&\color{blue}{10}
\end{eqnarray}\)
でも比例関係は崩れていません。

標本調査は推測になるので「およそ」がつきます。

(9)
\(\,2\,\)本の直線が平行になるための条件を探します。

「\(\,2\,\)本の直線が平行なら同位角と錯角が等しい。」
という関係は逆も成り立ちます。

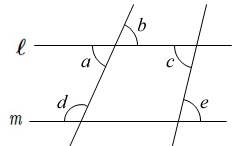
錯角である\(\,∠c\,\)と\(\,∠e\,\)が等しければ、
直線\(\,\ell\,\)と直線\(\,m\,\)が平行になるので
　\(\,∠\underline{　c　}\,\)と\(\,∠\underline{　e　}\,\)

ちなみに、平行でなくても同位角や錯角という言葉は使います。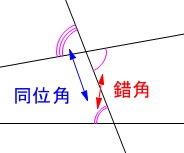平行なときに等しくなるだけです。

※
\(\,∠a=∠d(=90^{\circ})\,\)のときは平行にはなりますが、
問題は「右の図のように」明らかに直交していないときも、
どの角が等しければ「『いつも』平行と言えるか」を聞いています。

第２問関数の性質

\(\,2\,\)
比例と\(\,x^2\,\)に比例する関数の性質です。

(1)
\(\,y\,\)が\(\,x\,\)に比例するものを選びます。
　\(\hspace{10pt}y=ax\)
となっているものを選べば良いだけです。

すべて関数で表しておきます。

ア　自然数\(\,x\,\)の約数の個数\(\,y\,\)は比例していません。×
（いくつか自然数と約数の個数を書き並べると一定の関係式で表せないことが分かります。）

イ　\(y=1000-x\)　×
\(\,1\,\)次関数です。

ウ　\(\displaystyle y=\frac{1200}{x}\)　×
反比例です。

エ　\(\displaystyle y=5\times \frac{x}{100}=\frac{1}{20}\,x\)　○

オ　\(y=2x\)　○

答え　\(\,\underline{　エ　オ　}\,\)

(2)
関数\(\,y=2x^2\,\)について述べた文として正しいものを選びます。

簡単にグラフをかいて見れば済むことです。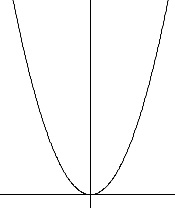
ア　原点を通ります。　○

イ　\(\,x\,＞\,0\,\)のとき\(\,x\,\)が増加すると\(\,y\,\)は増加します。　×

ウ　\(\,x\,\)軸対称ではなく、\(\,y\,\)軸対称です。　×

エ　\(\,y\,\)の変域は\(\,0\,≦\,y\,≦\,8\,\)です。　○

最小値は\(\,x=-1\,\)のときの\(\,y=2\,\)ではなく、
\(\,x=0\,\)のときの\(\,y=0\,\)です。

オ　変化の割合は一定ではなく変化し続けています。　×

変化の割合はグラフ上の\(\,2\,\)点間の傾きです。
比例定数の\(\,2\,\)は変化の割合ではありません。

答え　\(\,\underline{　ア　エ　}\,\)

それぞれ自分で書き込んで確認してください。

第３問文字式による倍数の証明

\(\,3\,\)
文字式による証明です。

例にあるように\(\,\mathrm{1331\,,\,7227}\,\)ような整数が\(\,11\,\)の倍数だということの証明です。

\(\,4\,\)けたの整数なので千の位の数は\(\,0\,\)ではないので条件がつきますが、
証明の続きを書きます。

（文字の設定が済んだ後）
　\(\hspace{4pt}1000a+100b+10b+a\,\)であり、
　\(\hspace{10pt}1000a+100b+10b+a\\
=1001a+110b\\
=11(91a+10b)\)
\(\,91a+10b\,\)は整数なので、
\(\,11(91a+10b)\,\)は\(\,11\,\)の倍数である。
（「したがって」に続く。）

とにかく文字で条件通りに表して、
\(\,11\,\)という因数で全体をくくれば良いのです。

ただし、残りの因数が分数や小数になると必ず整数とは言えないので
　「\(\,91a+10b\,\)は整数なので、」
という説明が必要になります。

第４問立体と距離の問題

\(\,4\,\)
直方体の問題です。

条件
　直方体\(\,\mathrm{ABCD-EFGH}\,\)
　\(\,\mathrm{AB=2}\,\)
　\(\,\mathrm{AD=4}\,\)
　\(\,\mathrm{AE=3}\,\)
（長さの単位は\(\,\mathrm{m}\,\)ですが途中計算では省略します。）

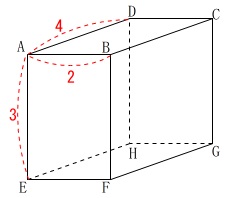
(1)
対角線\(\,\mathrm{AG}\,\)の長さを求めます。
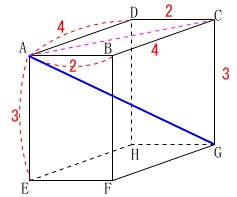面の対角線\(\,\mathrm{AC}\,\)を求めてから、
直角三角形\(\,\mathrm{ACG}\,\)に三平方の定理でも良いですが、
教科書でも公式化されているので直方体の対角線で良いでしょう。

　\(\begin{eqnarray}\displaystyle
\mathrm{AG}&=&\sqrt{2^2+3^2+4^2}\\
&=&\sqrt{4+9+16}\\
&=&\underline{　\sqrt{29}　\mathrm{m}}
\end{eqnarray}\)

(2)
\(\,\mathrm{A}\,\)から\(\,\mathrm{G}\,\)に糸を\(\,2\,\)通りの方法でかけます。

　ア　辺\(\,\mathrm{BC}\,\)を通るようにかける。
　イ　辺\(\,\mathrm{BF}\,\)を通るようにかける。

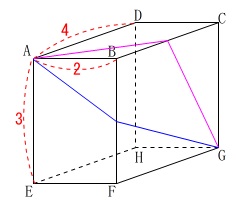
①
糸が最も短くになるのはア、イのどちらか選び、そのときの長さを求めます。

折れ線が最も短くなるのは平面にしたとき直線になるときです。
展開図で直線にすればそれぞれの最短距離が出ます。
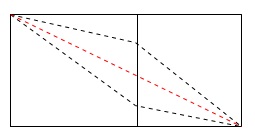\(\,2\,\)点間を最短でいくにはまっすぐ進んだ方が最短というのは直感的にも分かるでしょう。

ア
　\(\,\mathrm{BC}\,\)上の点を\(\,\mathrm{M}\,\)とすると、
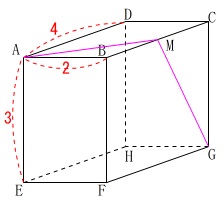\(\,\mathrm{AM＋MG}\,\)が最短になるのは展開図において
\(\,\mathrm{A-M-G}\,\)が直線になるときです。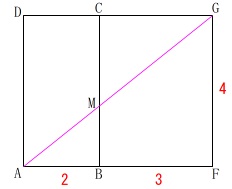このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{AG}&=&\sqrt{(2+3)^2+4^2}\\
&=&\sqrt{25+16}\\
&=&\color{magenta}{\sqrt{41}}
\end{eqnarray}\)

イ
　\(\,\mathrm{BF}\,\)上の点を\(\,\mathrm{N}\,\)とすると、
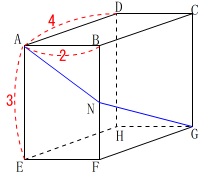\(\,\mathrm{AN＋NG}\,\)が最短になるのは展開図において
\(\,\mathrm{A-N-G}\,\)が直線になるときです。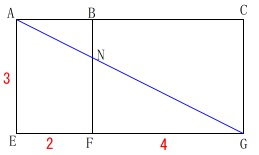このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{AG}&=&\sqrt{3^2+(2+4)^2}\\
&=&\sqrt{9+36}\\
&=&\color{blue}{\sqrt{45}}\\
&=&3\sqrt{5}
\end{eqnarray}\)

よって、
短いのは\(\,\underline{　ア　}\,\)で長さは\(\,\underline{　\sqrt{41}　\mathrm{m}}\,\)

主役は、展開図です。

②
①でかけた糸が長い方\(\,イ\,\)の場合を考えます。

かけた糸が面\(\,\mathrm{BFGC}\,\)を通る直線を\(\,\ell\,\)として、
点\(\,\mathrm{C}\,\)と\(\,\ell\,\)との距離を求めます。
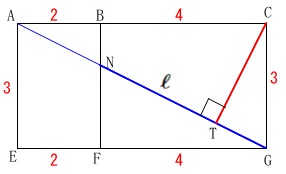点\(\,\mathrm{C}\,\)と直線\(\,\ell\,\)との距離は、
点\(\,\mathrm{C}\,\)から\(\,\ell\,\)に下ろした垂線の長さ\(\,\mathrm{CT}\,\)で、
\(\,\mathrm{△AGC}\,\)の底辺を\(\,\mathrm{AG}\,\)としたときの高さになります。

\(\,\mathrm{△AGC}\,\)の面積は底辺\(\,\mathrm{AC}\,\)、高さ\(\,\mathrm{CG}\,\)の直角三角形だから
　\(\begin{eqnarray}\displaystyle
\mathrm{△AGC}&=&\frac{1}{2}\times \mathrm{AC}\times \mathrm{CG}\\
&=&\frac{1}{2}\times (2+4)\times 3\\
&=&\color{red}{9}
\end{eqnarray}\)

また、
\(\,\mathrm{△AGC}\,\)は底辺を\(\,\mathrm{AG}\,\)とし、
高さを\(\,\mathrm{CT}\,\)としても面積は変わらないので、
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \mathrm{AG}\times \mathrm{CT}&=&\color{red}{9}\\
\frac{1}{2}\times 3\sqrt{5}\times \mathrm{CT}&=&9\\
3\sqrt{5}\times \mathrm{CT}&=&9\times 2\\
\mathrm{CT}&=&\frac{18}{3\sqrt{5}}\\
&=&\underline{　\frac{6\sqrt{5}}{5}　\mathrm{m}}
\end{eqnarray}\)

三角形の面積は底辺と高さを換えても変わらないことを利用しています。
体積でも良く使うので覚えておきましょう。

第５問円すいと相似な図形

\(\,5\,\)
円すいの相似と方程式の問題です。

条件（単位は\(\,\mathrm{cm}\,\)ですが省略します。）
　天井と床の間は\(\,300\,\)
　ライトを天井からひもでつりさげる。
　ライト\(\,\mathrm{A}\,\)は底面の直径\(\,8\,\)、高さ\(\,10\,\)の円すい
　ライト\(\,\mathrm{B}\,\)は底面の直径\(\,6\,\)、高さ\(\,10\,\)の円すい
　ライトから出た光は円すいの母線の延長までの範囲を照らす。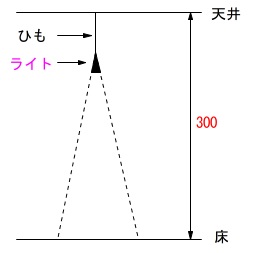
(1)
ライト\(\,\mathrm{A}\,\)をひもの長さ\(\,100\,\)でつるすとき、
ひかりが床を照らす円の直径を求めます。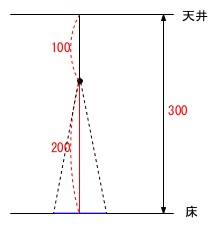ライトの円すいの頂点が一致する相似です。
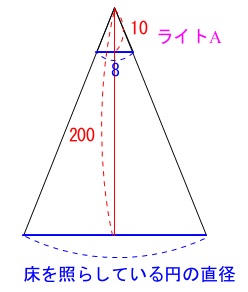床からの高さと円の直径は比例するので、
床の円の直径を\(\,a\,\)とすると
　\(\begin{eqnarray}\displaystyle
\color{red}{10}:\color{blue}{8}&=&\color{red}{200}:\color{blue}{a}\\
10a&=&200\times 8\\
a&=&\underline{　160　\mathrm{cm}}
\end{eqnarray}\)

比例なので時計回りに
　\(\displaystyle \color{blue}{8}\times \frac{\color{red}{200}}{\color{red}{10}}=a\)
としても良いです。

(2)
ライト\(\,\mathrm{A}\,\)を\(\,x\,\)のひもで吊り下げます。
ただし、\(\,50\,≦\,x\,≦180\,\)です。
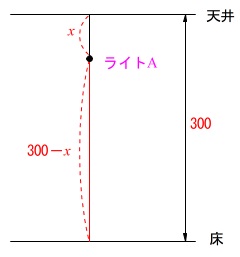円すいの頂点は床から\(\,300-x\,\)の高さになります。

①
高さと円の直径の比例関係は(1)と同じなので
　\(\begin{eqnarray}\displaystyle
10:8&=&(300-x):y\\
10y&=&8(300-x)\\
y&=&\frac{8(300-x)}{10}\\
&=&\frac{4(300-x)}{5}\\
&=&\underline{　240-\frac{4}{5}x　}
\end{eqnarray}\)
ただし、
　\(\,50\,≦\,x\,≦180\,\)

比例計算なので一気に
　\(\hspace{10pt}\displaystyle y=8\times \frac{300-x}{10}\)
とした人もいるでしょう。
間違いありませんので構いません。

②
①のとき\(\,50\,≦\,x\,≦180\,\)から\(\,y\,\)の変域は
　\(\hspace{4pt}\underline{　96\,≦\,y\,≦\,200　}\)

傾きが負なので
　\(\,x=180\,\)のとき\(\,y=96\,\)で最小
　\(\,x=50\,\)のとき\(\,y=200\,\)で最大
となります。

(3)
ライト\(\,\mathrm{A}\,\)とライト\(\,\mathrm{B}\,\)の照らすひかりの面積が等しくなるひもの長さを求めます。

　ライト\(\,\mathrm{A}\,\)をつるすひも\(\,x\,\)
　ライト\(\,\mathrm{B}\,\)をつするひも\(\displaystyle \,\frac{1}{2}x\,\)

ライト\(\,\mathrm{A}\,\)を\(\,x\,\)でつるす場合は(2)で関数にしています。
　\(\displaystyle \hspace{4pt}y=240-\frac{4}{5}x\)
です。

ライト\(\,\mathrm{B}\,\)を\(\displaystyle \,\frac{1}{2}x\,\)でつるすと、
床からの高さは\(\,\displaystyle \color{red}{300-\frac{1}{2}x}\,\)なので、
ライト\(\,\mathrm{B}\,\)の円すいの高さと底面の円の直径の比が、
　\(\,\color{red}{10}:\color{blue}{6}\,\)だから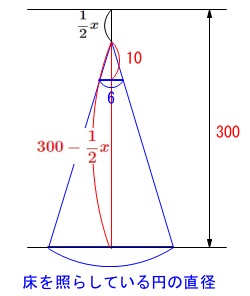床のひかりが照らす円の直径との比例関係から、
ライト\(\,\mathrm{B}\,\)の床を照らす円の直径を\(\,y_\mathrm{B}\,\)とすると
　\(\begin{eqnarray}\displaystyle
y_\mathrm{B}&=&180-\frac{3}{10}x
\end{eqnarray}\)
（(2)と同じ比例関係なので自分で出してみてください。）

直径が等しければ円の面積も等しくなるので、
　\(\begin{eqnarray}\displaystyle
240-\frac{4}{5}x&=&180-\frac{3}{10}x\\
2400-8x&=&1800-3x\\
-8x+3x&=&1800-2400\\
-5x&=&-600\\
x&=&\underline{　120　\mathrm{cm}}
\end{eqnarray}\)

問題になっているのは単なる比例関係なので、
問題のいっている状態がどう合っているか書き出すことがポイントです。

第６問平面図形と折り返し

\(\,6\,\)
半円と折り返しの問題です。

\(\,\mathrm{AB}\,\)が直径の半円があります。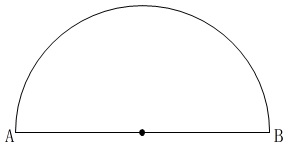
(1)
作図とその理由です。

\(\,\mathrm{弧AP:弧PB=1:2}\,\)となる点\(\,\mathrm{P}\,\)を弧\(\,\mathrm{AB}\,\)上に作図します。

手順
　\(\,ⅰ\,\)　直径\(\,\mathrm{AB}\,\)の中点\(\,\mathrm{O}\,\)をとる。
　\(\,ⅱ\,\)　\(\,\mathrm{AO=AP}\,\)となるような、弧\(\,\mathrm{AB}\,\)上の点\(\,\mathrm{P}\,\)をとる。

①
手順\(\,ⅰ\,\)によって\(\,\mathrm{AB}\,\)の中点、つまり中心\(\,\mathrm{O}\,\)を作図します。

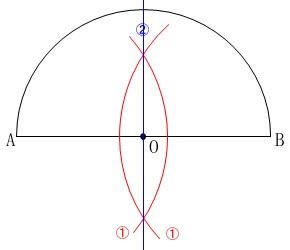
　\(\,\color{red}{①}\,\)　\(\,2\,\)点\(\,\mathrm{A,B}\,\)から\(\,2\,\)点で交わるように同じ半径の円をかく。
　\(\,\color{blue}{②}\,\)　\(\,\color{red}{①}\,\)の交点を結んで\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{O}\,\)とする。　
　
線分\(\,\mathrm{AB}\,\)の垂直二等分線を描いて、
\(\,\mathrm{AB}\,\)の中点（中心）を印しただけです。

②
手順\(\,ⅰ\,,\,ⅱ\,\)によって、なぜ、
　\(\,\mathrm{弧AP:弧PB=1:2}\,\)
になるのかの理由を説明します。

手順\(\,ⅰ\,\)では中心を見つけました。
つまり、\(\,\mathrm{AO}\,\)は半径です。

手順\(\,ⅱ\,\)で\(\,\mathrm{AO=AP}\,\)とすると、
半径はつねに等しいから\(\,\mathrm{OP=AO}\,\)でもあります。

このことから、
　\(\,\mathrm{△OAP}\,\)は正三角形で\(\,\mathrm{∠AOP=60^{\circ}}\,\)
となるから
　\(\,\mathrm{∠BOP=120^{\circ}}\,\)

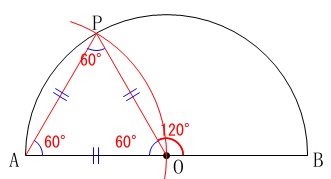
中心角の比が
　\(\begin{eqnarray}
\mathrm{∠AOP:∠BOP}&=&60^{\circ}:120^{\circ}\\
&=&1:2
\end{eqnarray}\)
となります。

また、中心角とその中心角に対する弧の長さは比例するので
　\(\hspace{4pt}\stackrel{\large{\frown}}{\mbox{AP}}\,:\,\stackrel{\large{\frown}}{\mbox{PB}}=1:2\)

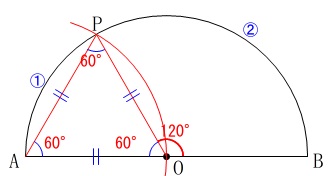
よって、手順\(\,ⅰ\,,\,ⅱ\,\)によって、
　\(\,\mathrm{弧AP：弧PB=1:2}\,\)
となります。

(2)
長さが加わり、部分の面積を求めます。

　直径の長さは\(\,\mathrm{AB=12}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）

①
(1)で作図した\(\,\mathrm{P}\,\)について、
弦\(\,\mathrm{PB}\,\)と弧\(\,\mathrm{PB}\,\)で囲まれた図形を弦\(\,\mathrm{PB}\,\)を折り目として折り、
元の半円と重なった部分の面積を求めます。
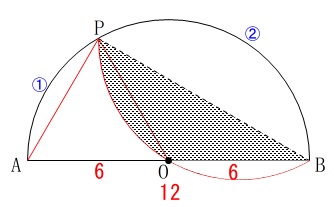影のついた部分です。

求め方はいろいろあります。

折角なのでここで復習しておきましょう。

「折る」というのは対称（線対称）な図形を作りますので、
対称性について見ていきます。
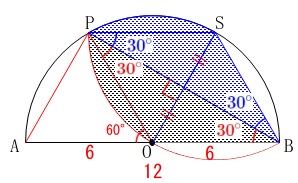折り返すと、
角度も辺もすべてが軸の反対側に移されます。

これが折り返し問題を考えるときの基本です。

影の部分の面積を求めるので、
折り返す元の図形の面積を考えましょう。
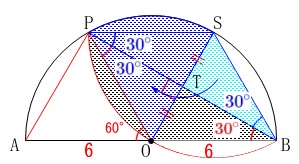\(\,\mathrm{PB,OS}\,\)の交点を\(\,\mathrm{T}\,\)とすると、
\(\,\mathrm{△STB}\,\)が\(\,\mathrm{△OTP}\,\)と合同なので移動できて、
求める面積\(\,S\,\)が中心角\(\,60°\,\)の扇形だと分かります。

円\(\,\mathrm{O}\,\)の面積は半径\(\,6\,\)なので
　\(\hspace{4pt}\pi\,(6)^2=36\pi\,\)
よって、
　\(\begin{eqnarray}\displaystyle
S&=&36\pi \times \frac{60}{360}\\
&=&\underline{　6\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)

この問題は折り返さなくても、
中心角\(\,60°\,\)の扇形に変形できるので簡単に答えが出ますが、
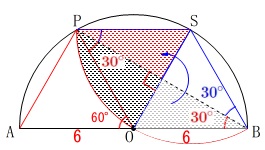折り返しの基本から復習しておきました。

三角形でも四角形でも折り返しの基本作業は変わりません。

②
\(\,\mathrm{弧AQ\,:\,弧QB=1:3}\,\)となる点\(\,\mathrm{Q}\,\)を弧\(\,\mathrm{AB}\,\)上にとります。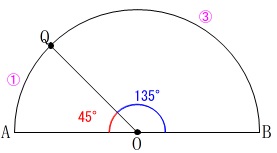
「①と同様に」
\(\,\mathrm{QB}\,\)を軸に折ります。

問題はよく読みましょう。
同様に折り返しているということは、
同じように求めれば良いということを伝えてくれているのです。

弧を\(\,1:3\,\)に分けているので、
中心角も\(\,1:3\,\)に分けられます。
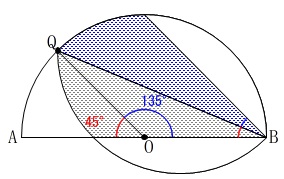折り返されているので角度も辺も折り返されます。
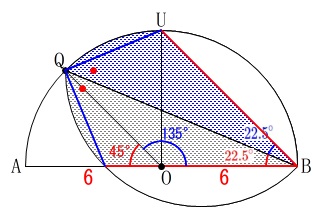半径は等しいので\(\,\mathrm{△OBQ}\,\)は二等辺三角形で
　\(\,\mathrm{∠OBQ=\color{red}{22.5^{\circ}}}\,\)
折り返しているので\(\,\mathrm{∠UBQ=\color{blue}{22.5^{\circ}}}\,\)でもあり、
　\(\hspace{4pt}\mathrm{∠UBO}=45^{\circ}\)

このとき\(\,\mathrm{△UOB}\,\)は直角二等辺三角形になります。
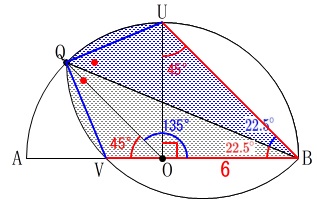求める面積は中心角を\(\,\mathrm{∠QOB}\,\)とする扇形から、
　\(\,\mathrm{△OBQ}\,\)と弦\(\,\mathrm{UB}\,\)と弧\(\,\mathrm{UB}\,\)で囲まれた部分
を引けば求まります。
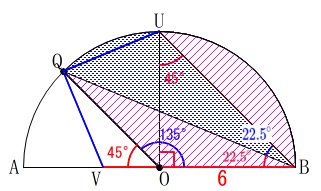\(\,\mathrm{△OBQ}\,\)の面積が欲しいので、
\(\,\mathrm{Q}\,\)から\(\,\mathrm{AB}\,\)に垂線を下ろし\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{R}\,\)とすると、
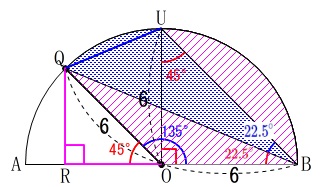\(\,\mathrm{△QRO}\,\)は直角二等辺三角形なので
　\(\,\mathrm{QR=OR}\,\)
かつ三角定規の比から
\(\,\mathrm{RQ：OQ=1:\sqrt{2}}\,\)なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{QR:OQ}&=&1:\sqrt{2}\\
\mathrm{QR}:6&=&1:\sqrt{2}\\
\sqrt{2}\mathrm{QR}&=&6\\
\mathrm{QR}&=&3\sqrt{2}
\end{eqnarray}\)

これは\(\,\mathrm{△OBQ}\,\)の高さで、底辺は\(\,\mathrm{OB}\,\)なので、
\(\,\mathrm{△OBQ}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S_1&=&\frac{1}{2}\times \mathrm{OB}\times \mathrm{QR}\\
&=&\frac{1}{2}\times 6\times 3\sqrt{2}\\
&=&\color{blue}{9\sqrt{2}}
\end{eqnarray}\)

また、
弦\(\,\mathrm{UB}\,\)と弧\(\,\mathrm{UB}\,\)で囲まれた部分の面積\(\,S_2\,\)は、
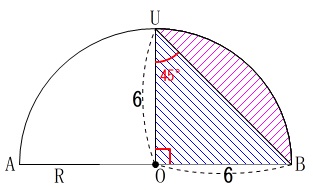四分円から直角二等辺三角形を引けば良いので
　\(\begin{eqnarray}\displaystyle
S_2&=&36\,\pi\times \frac{1}{4}-\frac{1}{2}\times 6\times 6\\
&=&\color{red}{9\,\pi-18}
\end{eqnarray}\)

中心角\(\,135°\,\)の扇形の面積\(\,S_3\,\)は
　\(\begin{eqnarray}\displaystyle
S_3&=&36\,\pi\times \frac{135}{360}\\
&=&36\,\pi \times \frac{3}{8}\\
&=&\frac{27}{2}\,\pi
\end{eqnarray}\)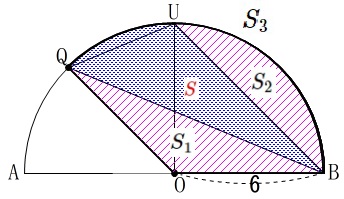よって、
求める面積\(\,\color{red}{S}\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&S_3-S_1-S_2\\
&=&\frac{27}{2}\,\pi-\color{blue}{9\sqrt{2}}-(\color{red}{9\,\pi-18})\\
&=&\underline{　\frac{9}{2}\,\pi-9\sqrt{2}+18　(\,\mathrm{cm^2}\,)}
\end{eqnarray}\)

折り返しというのは線対称だということを忘れなければ、
基本レポート程度の計算問題です。

ただ、
\(\,\mathrm{△UOB}\,\)が直角二等辺三角形だと気がついた後は、
折り返す前の（問題にある）影の部分で面積は出せます。

どちらでも良いですよ。
問題の「①と同様に」から『対称』というテーマにしておきました。

いつのまにか長くなってしまいましたが以上です。

細かい説明は必要無かったかもしれませんが、
平均点から少していねいにやっておきました。
（会員向けにチャチャっとしとけば良かった。）

⇒　2019年群馬県公立高校後期入試の数学の問題と解説

令和\(\,2\,\)年度の問題と解説です
令和\(\,\mathrm{3}\,\)年度も後期は出題範囲もほとんど変わりませんよ。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

群馬県の公立入試は計算がすごくハードで計算に追われるような問題ではありません。

「基本事項の定着を確実にして、問題の意味をしっかり読み取り、基本的な数学の作業をしてください。」
と、群馬県の公立入試はいっています。