2020年度福岡県公立高校入試数学の問題と解説

2020年（令和2年）度に福岡県で行われた公立高校入試数学の問題と解説です。
偏りのない教科書全範囲からのバランスの良い出題となっています。
空間図形を苦手にしている人が多いですが、
きれいな数値で与えられているので落ち着いて取り組めば難問ではありません。

2020年度福岡県公立高校入試数学の問題

\(\,2020\,\)年度福岡県立高校入試の数学問題です。

⇒　2020年度福岡県立高校入試の数学の問題

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。

どれも計算力だけで差をつけるような見にくい数値はありませんので、
しっかり考えて作業すればすんなり答えが出るように問題が作られています。

2020年度福岡県公立高校入試数学の解説

計算に時間がかかるような問題はそれほど見当たりませんので、
計算力よりほんの少しの作業量で差がつく問題です。

空間図形の得点率が低いのは時間配分を間違えたのでしょう。
それほど解説が必要とも思えませんので一気に終わらせます。

第１問計算が主な小問集合

\(\color{black}{\fbox{1}}\)
式の計算と方程式、反比例、データの活用の\(\,9\,\)問です。

(1)
　\(\hspace{10pt}8+\color{red}{2\times (-7)}\\
=8\color{red}{-14}\\
=\underline{　-6　}\)

掛け算部分が先です。

(2)
　\(\hspace{10pt}2(a+4b)-(5a+b)\\
=2a+8b-5a\color{red}{-b}\\
=\underline{　-3a+7b　}\)

展開して同類項をまとめるだけですが、
符号を間違えないように\(\,2\,\)行目はしっかり書いておきましょう。

(3)
　\(\hspace{10pt}\displaystyle \sqrt{75}-\frac{9}{\sqrt{3}}\\
\displaystyle =5\sqrt{3}-\frac{9\times \color{red}{\sqrt{3}}}{\sqrt{3}\times \color{red}{\sqrt{3}}}\\
\displaystyle =5\sqrt{3}-\frac{9\sqrt{3}}{3}\\
=5\sqrt{3}-3\sqrt{3}\\
=\underline{　2\sqrt{3}　}\)

なれている人は\(\,2\,\)行目は飛ばして良いです。
ただし、素因数分解はきっちりやりましょう。

(4)
　\(\begin{eqnarray}
3(2x-5)&=&8x-1\\
6x\color{blue}{-15}&=&\color{red}{8x}-1\\
6x\color{red}{-8x}&=&-1\color{blue}{+15}\\
-2x&=&14\\
x&=&\underline{　-7　}
\end{eqnarray}\)

単なる\(\,1\,\)次方程式です。
左辺に文字式、右辺に定数項を集める、で良いですよ。

(5)
　\(\begin{eqnarray}\displaystyle
2a+3b&=&1\\
2a&=&1-3b\\
a&=&\underline{　\frac{1-3b}{2}　}
\end{eqnarray}\)

答えは
　\(\hspace{10pt}\displaystyle a=\frac{1}{2}-\frac{3}{2}b\)
でも良いですが、手間が増えるだけです。

\(\,a\,\)について解く場合は\(\,b\,\)は定数扱いですよ。

(6)
関数は反比例です。
　\(\displaystyle y=\frac{\color{red}{a}}{x}\)
先ずは比例定数\(\,\color{red}{a}\,\)を求めましょう。

表中のどれでも良いですが
　\(\,(-2\,,\,6)\,\)
を代入します。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{a}{x}\\
-2&=&\frac{a}{6}\\
\color{red}{a}&=&-12
\end{eqnarray}\)

関数は
　\(\hspace{10pt}\displaystyle y=\frac{-12}{x}\)
となるので\(\,x=3\,\)のとき
　\(\hspace{10pt}\displaystyle y=\frac{-12}{3}=\underline{　-4　}\)

反比例ではいつも
　\(xy=\color{red}{a}　(一定)\)
となります。

(7)
放物線のグラフは\(\,3\,\)点を記入すれば良いのですが、
頂点が分かっている場合は、頂点と他の\(\,1\,\)点で良いです。
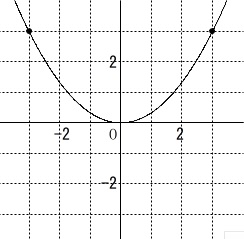目盛りがついている場合は必ず通る点\(\,(\,\pm3\,,\,3)\,\)と
　\(\,x=1\,\)のとき、\(\,y=\displaystyle \frac{1}{3}\,\)
　\(\,x=2\,\)のとき、\(\,y=\displaystyle \frac{4}{3}\,\)
　\(\cdots\)
とおおよそで良いので位置を押させておきましょう。
\(\,y\,\)軸を軸として対称となるグラフなので、
あまりにも放物線としておかしい場合は○にはなりません。

(8)
度数分布表から相対度数を比較します。
　\(\displaystyle (\,相対度数\,)=\frac{　(\,度数\,)　}{　(\,度数合計\,)　}\)
階級は\(\,30\,\)以上\(\,60\,\)未満だけを見れば良いです。

\(\,\mathrm{A}\,\)中学校の相対度数は
　\(\hspace{10pt}\displaystyle \frac{25}{85} =\color{red}{\frac{5}{17}}\\
=0.294\cdots\)

\(\,\mathrm{B}\,\)中学校の相対度数は
　\(\hspace{10pt}\displaystyle \frac{32}{136} =\color{blue}{\frac{4}{17}}\\
=0.235\cdots\)

相対度数は\(\,\mathrm{A}\,\)中学校の方が大きく、
　\(\hspace{10pt}\underline{　0.29　}\)

分数で大小を見分けましたが最初から割り算しても良いですよ。
\(\,\mathrm{B}\,\)中学校の相対度数を小数で表す必要はなかったのですが、
割り算した人もいるだろうから確認のため割り算しておきました。

第２問文字式と方程式

\(\color{black}{\fbox{2}}\)
花だんの中に道を作る良くある問題です。

条件
　長方形の土地の横の長さは縦の長さの\(\,2\,\)倍。
　縦の長さを\(\,x\,\)とする。
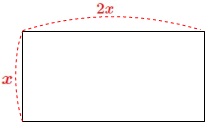このとき、縦が\(\,\color{red}{x}\,\)、横が\(\,\color{red}{2x}\,\)になることは良いでしょう。

(1)
計算してしまうとわかりにくくなりますが、
計算式そのままで表してあるので簡単です。
　縦\(\,x\,\)と横\(\,2x\,\)を足して\(\,2\,\)倍
　\(\hspace{4pt}(x+2x)\times 2\)
してあるので周の長さです。

答え　\(\,\underline{　ア　}\,\)

(2)
花だんの面積と道の面積のどちらでも方程式を立てて、
土地の縦の長さを求めます。

条件
　道幅\(\,2\,\)で縦横に道を作る。
　残りの花だんの面積が\(\,264\,\)になった。
（単位は\(\,\mathrm{m}\,\)ですが省略します。）
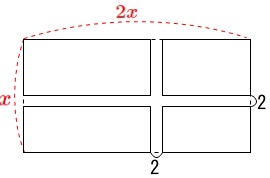部分部分を足しても良いのですが、
道を端にずらします。

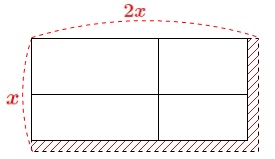
道幅が\(\,2\,\)なので
　花だんの縦は\(\,\color{blue}{x-2}\,\)
　花だんの横は\(\,\color{blue}{2x-2}\,\)
になります。

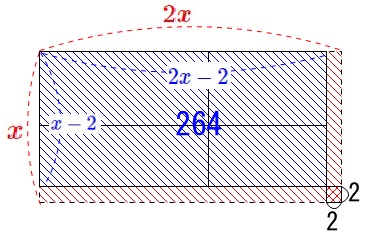
\(\,ア\,\)　花だんの面積で方程式を立てます。

花だんの面積が\(\,\color{blue}{264}\,\)なので
　\(\begin{eqnarray}\displaystyle
(x-2)(2x-2)&=&264\\
2(x-2)(x-1)&=&264\\
(x-2)(x-1)&=&132\\
x^2-3x+2&=&132\\
x^2-3x-130&=&0\\
(x+10)(x-13)&=&0\\
\end{eqnarray}\)
長さなので\(\,x\,＞\,0\,\)だから
　\(\hspace{10pt}x=\underline{　13　m}\)

\(\,イ\,\)　道の面積で方程式立てます。

全体の面積から花だの面積\(\,\color{blue}{264}\,\)を引けば道の面積になるので、
右下の正方形（道が重なっている部分）\(\,\color{red}{4}\,\)が\(\,2\,\)回数えられていることに注意して、
　\(\begin{eqnarray}\displaystyle
x(2x)-\color{blue}{264}&=&2(x+2x)-\color{red}{4}\\
2x^2-264&=&2x+4x-4\\
2x^2-6x-260&=&0\\
x^2-3x-130&=&0
\end{eqnarray}\)

答えは同じです。　\(\underline{　13　\mathrm{m}}\)

道幅が\(\,2\,\)なので、
　縦が\(\,x\,\)だから道の縦で\(\,2\times x\,\)
　横が\(\,2x\,\)だから道の横で\(\,2\times 2x\,\)
これを合わせて道の面積の右辺では
　\(2(x+2x)\)
とまとめて表しています。
（式が横長になるのでまとめただけなので普通に書いて良いです。）

第３問組み合わせと確率

\(\color{black}{\fbox{3}}\)
\(\,2\,\)枚のカードを取り出し、
\(\,2\,\)枚の数の和だけコマを動かすときの組合わせと確率です。

条件
　マスは\(\,\mathrm{A,B,C,D}\,\)の4つ。
　箱にはカードは\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)が1枚ずつ。
　最初\(\,\mathrm{A}\,\)にコマをおく。
　\(\,2\,\)枚のカードを同時に取り出す。
　\(\,\mathrm{A}\,\)から\(\,\mathrm{B,C,D,A\,\cdots}\,\)の順に\(\,2\,\)数の和だけ動く。
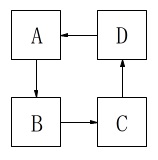\(\,\mathrm{A}\,\)から順に動きますが、
\(\,2\,\)数の和は
　\(\,3,4,5,6,7,8,9\,\)
しかなくて、
　\(\,\mathrm{B}\,\)に止まるのは和が\(\,5,9\,\)
　\(\,\mathrm{C}\,\)に止まるのは和が\(\,6\,\)
　\(\,\mathrm{D}\,\)に止まるのは和が\(\,3,7\,\)
　\(\,\mathrm{A}\,\)に止まるのは\(\,4,8\,\)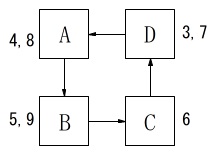
のときだけだと分かれば、
5つの数字の組み合わせは\(\,10\,\)通りしかないので、
書き出した方が早いです。

樹形図で良いですが表にしておきます。

(1)
コマが\(\,\mathrm{D}\,\)に止まる組み合わせです。

　\(\begin{array}{|c|c|C_} \hline
カード & カード & 和 & 止まる位置 \\ \hline
1 & 2 & 3 & \color{red}{\mathrm{D}} \\ \hline
1 & 3 & 4 & \mathrm{A} \\ \hline
1 & 4 & 5 & \mathrm{B}\\ \hline
1 & 5 & 6 & \mathrm{C}\\ \hline
2 & 3 & 5 & \mathrm{B}\\ \hline
2 & 4 & 6 & \mathrm{C}\\ \hline
2 & 5 & 7 & \color{red}{\mathrm{D}}\\ \hline
3 & 4 & 7 & \color{red}{\mathrm{D}}\\ \hline
3 & 5 & 8 & \mathrm{A}\\ \hline
4 & 5 & 9 & \mathrm{B}\\ \hline
\end{array}\)

組合わせ\(\,(\,1\,,\,2\,)\,\)以外の２つは
　\(\underline{　(\,2\,,\,5\,)\,(\,3\,,\,4\,)　}\)

(2)
\(\,\mathrm{A、C}\,\)の止まる確率をそれぞれ出して、
どちらに止まりやすいかを求めます。

\(\,5\,\)枚のカードが
　\(\,1,2,3,3,5\,\)
になります。

\(\,3\,\)が\(\,2\,\)枚あるので\(\,3\,\)が取り出される確率は、
他の数字とは同じではありません。

そこで2つの\(\,3\,\)を区別します。
　\(\,\color{red}{3a}\,,\,\color{blue}{3b}\,\)
とすると取り出し方は

　\(\begin{array}{|c|c|C_} \hline
カード & カード & 和 & 止まる位置 \\ \hline
1 & 2 & 3 & \mathrm{D} \\ \hline
1 & \color{red}{3a} & 4 & \mathrm{A} \\ \hline
1 & \color{blue}{3b} & 4 & \mathrm{A}\\ \hline
1 & 5 & 6 & \mathrm{C}\\ \hline
2 & \color{red}{3a} & 5 & \mathrm{B}\\ \hline
2 & \color{blue}{3b} & 5 & \mathrm{B}\\ \hline
2 & 5 & 7 & \mathrm{D}\\ \hline
\color{red}{3a} & \color{blue}{3b} & 6 & \mathrm{C}\\ \hline
\color{red}{3a} & 5 & 8 & \mathrm{A}\\ \hline
\color{blue}{3b} & 5 & 8 & \mathrm{A}\\ \hline
\end{array}\)

\(\,\mathrm{A}\,\)に止まる確率は
　\(\displaystyle \frac{4}{10}=\frac{2}{5}\)

\(\,\mathrm{C}\,\)に止まる確率は
　\(\displaystyle \frac{2}{10}=\frac{1}{5}\)

よって、コマが止まりやすいのは
　\(\,\underline{　\mathrm{A}　}\,\)

いつも通り樹形図で良いですよ。

第４問１次関数

\(\color{black}{\fbox{4}}\)
基本料金と分ごとの通話料が加わる\(\,1\,\)次関数問題です。

与えられた条件から\(\,\mathrm{A,B,C}\,\)の\(\,1\,\)次関数を求めれば終わります。
ただし、通話時間によって分単位の料金が変わるのでそこだけ気をつけましょう。
（単位は円ですが省略します。）

(1)
\(\,\mathrm{A}\,\)プランでは
　基本料金\(\,1200\,\)
と通話料金が、
　\(\,60\,\)分までは\(\,1\,\)分あたり\(\,40\,\)
　\(\,60\,\)分を超えると\(\,1\,\)分あたり\(\,30\,\)
に変わります。

\(\,\mathrm{A}\,\)についてはグラフがあるので読み取れば良いです。

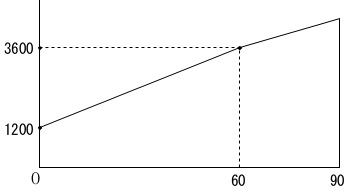
\(\,60\,\)分までは
　\(\,(\,0\,,\,1200\,)\,\)
　\(\,(\,60\,,\,3600\,)\,\)
を通るので、
　\(\,y=40x+1200\,\)

\(\,y=3000\,\)のときはこの区間にあるので
　\(\begin{eqnarray}\displaystyle
3000&=&40x+1200\\
40x&=&1800\\
x&=&\underline{　45　分}
\end{eqnarray}\)

\(\,60\,\)分後からは\(\,1\,\)分\(\,30\,\)なので
\(\,30\,\)分で\(\,900\,\)高くなるから
　\(\,(\,90\,,\,4500\,)\,\)
を通るので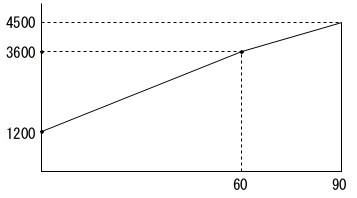
　\(\,(\,60\,,\,3600\,)\,\)
との\(\,2\,\)点を通る直線は
　\(y=30x+1800\)

これは後で使いますが、求まる関数はすべて求めておきます。

(2)
(1)と同じでグラフから区間ごとの関数を読み取る問題です。

\(\,x,y\,\)の関係が書かれています。
　
　\(\,0\,≦\,x\,≦\,20\,\)のとき\(\,y=2300\,\)
　\(\,20\,≦\,x\,≦\,90\,\)のとき\(\,y=ax+b\,\)
　\(\,x=60\,\)のとき\(\,y=3300\,\)

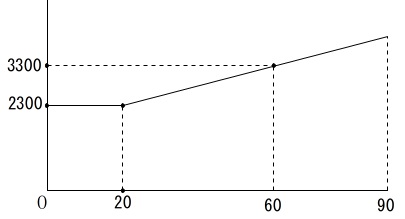
これは基本料金が\(\,2300\,\)で\(\,20\,\)分が通話料無料で、
\(\,20\,\)分から\(\,60\,\)分の\(\,40\,\)分間で\(\,1000\,\)上がっているので、
この区間では\(\,1\,\)分で\(\,25\,\)上がることを意味しています。

答え
　（ア）\(\,\underline{　2300　}\,\)
　（イ）\(\,\underline{　20　}\,\)
　（ウ）\(\,\underline{　25　}\,\)

ややこしく見えますが、\(\,2\,\)直線はつながっていて
　\(\,(\,0\,,\,2300\,)\,　･･･①\)
　\(\,(\,20\,,\,2300\,)\,　･･･②\)
　\(\,(\,60\,,\,3300\,)\,　･･･③\)
を通っています。

①②を通る直線が
　\(\,y=2300\,\)（定直線）
②③を通る直線\(\,y=ax+b\,\)が
　\(\,y=25x+1800\)

(3)
\(\,\mathrm{C}\,\)プランは
　基本料金が\(\,3900\,\)
　\(\,60\,\)分までは通話無料
　\(\,60\,\)分を超えたら\(\,1\,\)分あたり一定の料金がかかる。

この一定の料金\(\,\color{blue}{a}\,\)を求めておけば良いのです。

\(\,\mathrm{C}\,\)の関数は
　\(\,(\,60\,,\,3900\,)\,\)
　\(\,(\,90\,,\,4350\,)\,\)
を通るので\(\,30\,\)分で\(\,450\,\)上がるので
　\(\displaystyle \color{blue}{a}=\frac{450}{30}=15\)
これが直線の傾きで、
\(\,60≦x≦90\,\)の区間の関数は
　\(\,y=15x+3000\,\)

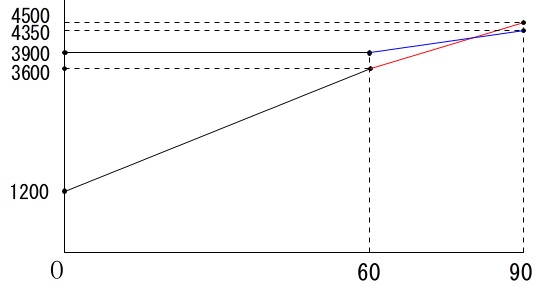
\(\,\mathrm{A}\,\)プランと\(\,\mathrm{C}\,\)プランの料金が同じになるのは
　\(\,y=30x+1800　(\,60\,≦\,x\,≦\,90\,)\)
　\(\,y=15x+3000　(\,60\,≦\,x\,≦\,90\,)\,\)
が交わるときで、
（グラフからは明らかに\(\,60\,\)分から\(\,90\,\)分にある。）
　\(\begin{eqnarray}\displaystyle
30x+1800&=&15x+3000\\
15x&=&1200\\
&=&80　分
\end{eqnarray}\)

これは\(\,60\,\)分から\(\,90\,\)分までの間にあるので適している。

これより多く通話する場合は\(\,\mathrm{C}\,\)プランの方が安くなります。

答え　\(\,\underline{　80　分}\,\)

ただ、\(\,2\,\)点を通る直線を求め続けただけです。

第５問平面図形

\(\color{black}{\fbox{5}}\)
対称な図形の意味と相似の証明と面積を求める平面図形の問題です。

(1)
角の二等分線を引く作図の意味です。

　\(\,\color{red}{①}\,\)\(\,\mathrm{B}\,\)を中心に円をかき、\(\,\mathrm{AB,CB}\,\)との交点を\(\,\mathrm{M,N}\,\)とする。
　\(\,\color{blue}{②}\,\)\(\,\mathrm{M}\,\)を中心に\(\,\color{red}{①}\,\)の半径より大きい円をかく。
　\(\,\color{magenta}{③}\,\)\(\,\mathrm{N}\,\)を中心に\(\,\color{blue}{②}\,\)と同じ半径の円をかく。
　\(\,④\,\)\(\,\color{blue}{②}\color{magenta}{③}\,\)の交点\(\,\mathrm{P}\,\)と\(\,\mathrm{B}\,\)を結ぶ直線をひく。
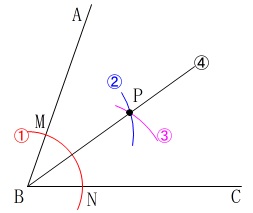直線\(\,\mathrm{BP}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線です。

作図の課程を見ていくとわかります。

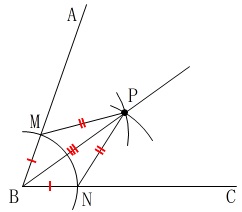
\(\,3\,\)辺がそれぞれ等しいので
　\(\,\mathrm{△MBP}\,\)≡\(\,\mathrm{△NBP}\,\)
だから
　\(\,\mathrm{∠ABP=∠CBP}\,\)
になります。

会話にあてはめると、
　四角形\(\,\mathrm{PMBN}\,\)が直線\(\,\mathrm{BP}\,\)を対称の軸とする線対称
な図形だから。

答え　\(\,\underline{　ウ　}\,\)

単に「対称」という場合は線対称を意味しますので注意して使って下さい。

(2)
これは作図の課程の意味を書き出せば終わりです。
　\(\,\color{red}{①}\,\)で\(\,\mathrm{BM=BN}\,\)となる点\(\,\mathrm{M,N}\,\)を探した。
　\(\,\color{blue}{②}\color{magenta}{③}\,\)で\(\,\mathrm{MP=NP}\,\)となる\(\,\mathrm{P}\,\)を探した。
　また、\(\,\mathrm{BP}\,\)は共通な辺
なので\(\,3\,\)辺がそれぞれ等しいことが言えます。

答え　
　\(\,\mathrm{\underline{　BM=BN　}}\,\)
　\(\,\mathrm{\underline{　MP=NP　}}\,\)

ここまでは理由も何もありません。
作図で何をしたのか書いただけです。

(3)
相似の証明です。

条件が割と多いので証明は簡単です。

条件
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EG}\,\)

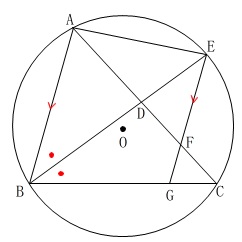
後は問題にある図の通りの記号が与えられています。

　\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△FAE}\,\)を証明します。

このサイトのどこでも言っていますが、
証明は図の中で仕上げておくことです。

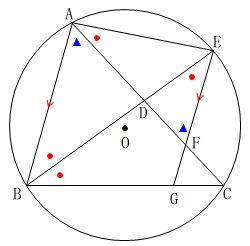
（証明）
　\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△FAE}\,\)において
直線\(\,\mathrm{BE}\,\)が\(\,\mathrm{∠ABC}\,\)の二等分線なので
　\(\,\mathrm{∠ABD=\color{red}{∠CBD}}\,　･･･①\)
弧\(\,\mathrm{CE}\,\)に対する円周角は等しいから
　\(\,\mathrm{∠FAE=\color{red}{∠CBD}}　･･･②\)
①②から
　\(\,\mathrm{∠ABD=∠FAE}　･･･③\)
また、\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EG}\,\)なので錯角が等しく
　\(\,\mathrm{∠BAD=∠AFE　･･･④}\,\)
③④より、
　\(\,2\,\)組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABD}\,\)∽\(\,\mathrm{△FAE}\,\)
（証明終わり）

相似と合同の証明での中で大切なのは2つあります。

　記号の順番を合わせること。
と
　相似または合同条件を書く。

後は図の中で示したことを適当に書き並べれば、
どのような形式でも論理が正しければ減点されることはありません。

(4)
(3)で与えられた図に条件が加わります。

加わる条件
　\(\,\mathrm{∠ABC=60^{\circ}}\,\)
　\(\,\mathrm{BE}\,\)は円\(\,\mathrm{O}\,\)の直径
　\(\,\mathrm{△ABC=15　\mathrm{cm^2}}\,\)

（長さの単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。）

(3)の条件はまだ続いているので、
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EG}\,\)
は使えます。

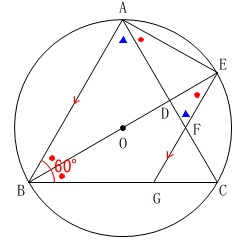
　\(\,\mathrm{∠ABC=60^{\circ}}\,\)
なので
　\(\,\mathrm{△ABC}\,\)が正三角形
で面積が\(\,15\,\)なので\(\,1\,\)辺の長さを求めたくなりますが、
実は長さは必要ありません。

この図形には二等辺三角形と三角定規がたくさんあります。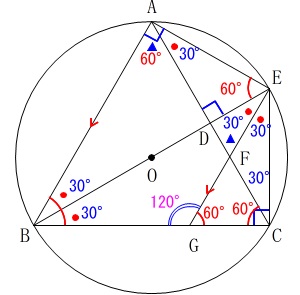
\(\,\mathrm{△CGF}\,\)と\(\,\mathrm{△ABC}\,\)が正三角形であることと、
\(\,\mathrm{△GBE}\,\)と\(\,\mathrm{△FCE}\,\)が二等辺三角形であること、
さらに\(\,\mathrm{△CGE}\,\)が三角定規であることから、
　\(\,\mathrm{CG}=\color{red}{a}\,\)
とすると\(\,\mathrm{△GBE}\,\)は二等辺三角形なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BG}&=&\mathrm{GE}\\
&=&2\times \mathrm{CG}\\
&=&\color{red}{2\,a}\\
\end{eqnarray}\)

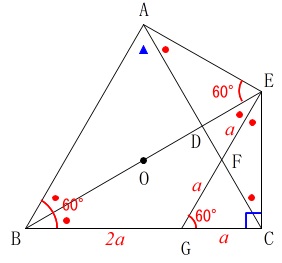
このことから2つの正三角形
\(\,\mathrm{△FGC}\,\)と\(\,\mathrm{△ABC}\,\)の相似比は
　\(\,\mathrm{GC:BC=1:3}\,\)
面積比は
　\(\,\mathrm{1^2:3^2=1:9}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△FGC}&=&\frac{1}{9}\times \mathrm{△ABC}\\
&=&\frac{1}{9}\times 15\\
&=&\color{red}{\frac{5}{3}}
\end{eqnarray}\)

また\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△BCD}\,\)の面積は\(\,\mathrm{△ABC}\,\)の半分なので
　\(\displaystyle\,\mathrm{△ABD}=\mathrm{△BCD} =\color{blue}{\frac{15}{2}}\)

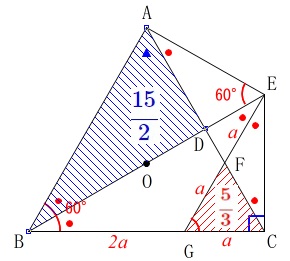
よって、求める四角形\(\,\mathrm{BGFD}\,\)の面積\(\,\mathrm{S}\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△BCD-△FGC}\\
&=&\color{blue}{\frac{15}{2}}-\color{red}{\frac{5}{3}}\\
&=&\frac{45-10}{6}\\
&=&\underline{　\frac{35}{6}　\mathrm{cm^2}}
\end{eqnarray}\)

比だけで出しました。

というより、
\(\,\mathrm{△ABC}\,\)の面積が\(\,15\,\)なので
正三角形の\(\,1\,\)辺は求められないのではないですか？

正三角形の\(\,1\,\)辺を何かで表し、
相似を繰り返し利用しても出てきます。

他にも正三角形の相似比にたどり着く手順はありますが、
どの方法でも四角形\(\,\mathrm{BGFD}\,\)は公式が使える形はしていないので、
　「全体－部分」
や
　「部分＋部分」
の公式が使える面積を利用する方法になりますね。

第６問空間図形

\(\color{black}{\fbox{6}}\)
空間図形の問題で、位置関係、錐台の体積、線分の長さを求めます。

直方体なので扱いやすいです。

直方体の辺の長さ
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{BC=4}\,\)
　\(\,\mathrm{AE=3}\,\)

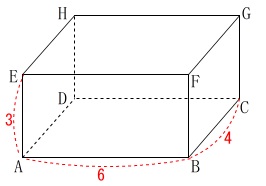
(1)
位置関係を正しく述べている記号を選びます。

ア　「面\(\,\mathrm{ABFE}\,\)と辺\(\,\mathrm{DH}\,\)は垂直である。」
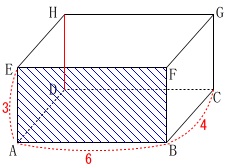平行です。×

イ　「辺\(\,\mathrm{AB}\,\)と辺\(\,\mathrm{AD}\,\)は垂直である。」
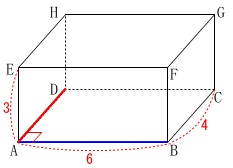辺\(\,\mathrm{AD}\,\)は面\(\,\mathrm{ABFE}\,\)そのものと垂直です。○

ウ　「面\(\,\mathrm{ADHE}\,\)は面\(\,\mathrm{BCGF}\,\)は平行である。」
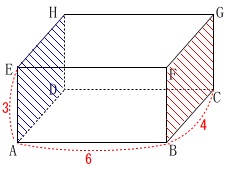直方体の対面になるので平行です。○

エ　「辺\(\,\mathrm{ＣＤ}\,\)と辺\(\,\mathrm{ＥＦ}\,\)はねじれの位置にある。」
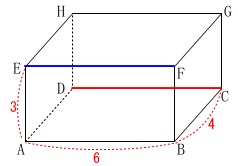交わることはありませんが平行です。
ねじれの位置にはありません。×

答え　\(\,\underline{　イ　ウ　}\,\)

(2)
直方体を平面で切った図形の体積を求めます。

条件
　\(\,\mathrm{EF}\,\)の中点を\(\,\mathrm{M}\,\)
　\(\,\mathrm{FG}\,\)の中点を\(\,\mathrm{N}\,\)
　\(\,4\,\)点\(\,\mathrm{A,C,N,M}\,\)を通る平面で直方体を分ける。

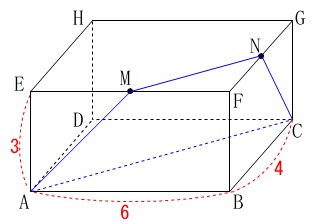
問題に\(\,4\,\)点\(\,\mathrm{A,C,N,M}\,\)が、
同じ平面上にあることを書いているので分かり易いです。

中点連結定理から
　\(\,\mathrm{MN}\,\)∥\(\,\mathrm{EG}\,\)
また
　\(\,\mathrm{EG}\,\)∥\(\,\mathrm{AC}\,\)
なので同一平面にあります。
ここは迷わず平面で切って進んで下さいという作成者が親切に書いてくれた訳です。

頂点\(\,\mathrm{F}\,\)を含む立体は三角錐の一部です。

辺\(\,\mathrm{BF}\,\)、\(\,\mathrm{AM}\,\)、\(\,\mathrm{CN}\,\)を延長すると\(\,1\,\)点で交わります。
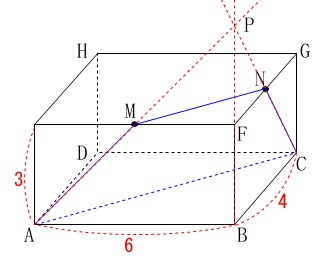底面を\(\,\mathrm{ABC}\,\)と見たとき、
3つの側面は中点連結定理により、
辺\(\,\mathrm{BF}\,\)、\(\,\mathrm{AM}\,\)、\(\,\mathrm{CN}\,\)を\(\,2\,\)倍にした点\(\,\mathrm{P}\,\)で交わります。
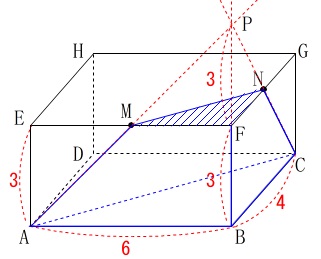三角錐\(\,\mathrm{P-MFN}\,\)と三角錐\(\,\mathrm{P-ABC}\,\)は相似で、
相似比
　\(\,\mathrm{PF:PB=1:2}\,\)
なので体積比は
　\(\,1^3:2^3=1:8\,\)

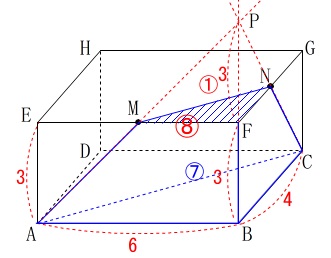
三角錐\(\,\mathrm{P-ABC}\,\)の体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{PB}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 4\times 6\\
&=&24
\end{eqnarray}\)

この体積から体積比\(\,\color{red}{①}:\color{red}{⑧}\,\)の\(\,\color{red}{①}\,\)にあたる上の三角すいを除くことになるので、
台になっている下の部分の体積は、
全体を\(\,\color{red}{⑧}\,\)としたとき\(\,\color{blue}{⑦}\,\)になります。

よって求める立体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&24\times \frac{7}{8}\\
&=&\underline{　21　\mathrm{cm^2}}
\end{eqnarray}\)

まだまだきれいな数字だけで問題が作られています。

(3)
立体中の線分\(\,\mathrm{IJ}\,\)の長さを求めます。

直方体の条件は変わらず、条件が加わります。

条件
　\(\,\mathrm{EI=1}\,\)
　\(\,\mathrm{DJ:JG=1:2}\,\)
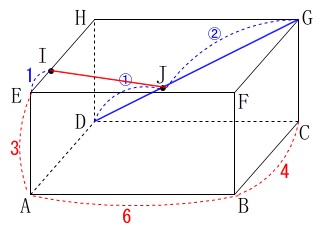\(\,\mathrm{DG}\,\)は長方形\(\,\mathrm{CGHD}\,\)の対角線で面の中にあるので簡単です。

平面を抜き出して作業するのが基本ですが、
分かり易いので立体のまま進めます。

\(\,\mathrm{J}\,\)から\(\,\mathrm{GH}\,\)に垂線を引いて、
\(\,\mathrm{HG}\,\)との交点を\(\,\mathrm{K}\,\)とすると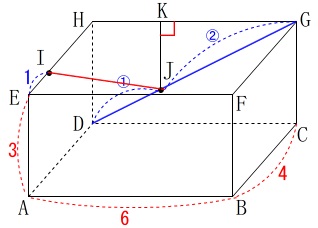　\(\,\mathrm{△GKJ}\,\)∽\(\,\mathrm{△GHD}\,\)
なので条件の\(\,\mathrm{DJ:JG=1:2}\,\)から、
　\(\,\mathrm{HK:KG=1:2}\,\)
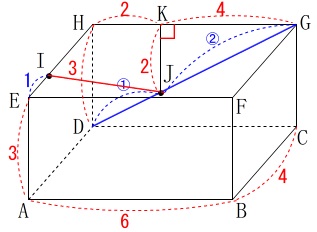
なので\(\,\mathrm{HG=\color{red}{6}}\,\)であることから
　\(\hspace{4pt}\mathrm{HK}=\color{red}{2}\)

同じように、
　\(\,\mathrm{HD:KJ=3:2}\,\)
なので
　\(\hspace{4pt}\mathrm{KJ}=\color{red}{2}\)
ここで\(\,\mathrm{IJ}\,\)は直方体の対角線になるので、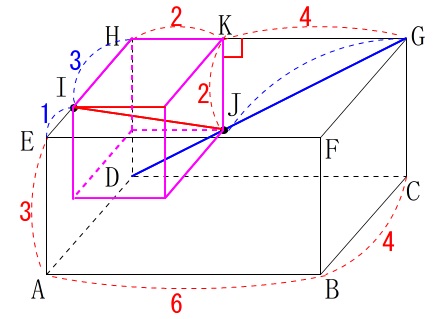
　\(\begin{eqnarray}\displaystyle
\mathrm{IJ}&=&\sqrt{\mathrm{KJ^2+HK^2+IH^2}}\\
&=&\sqrt{2^2+2^2+3^2}\\
&=&\sqrt{4+4+9}\\
&=&\underline{　\sqrt{17}　\mathrm{cm}}
\end{eqnarray}\)

基本通り平面を抜き出して進めると、
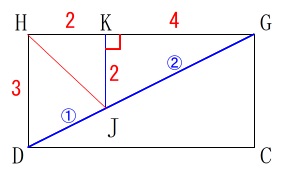三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{HJ}&=&\sqrt{\mathrm{HK^2+KJ^2}}\\
&=&\sqrt{2^2+2^2}\\
&=&\color{magenta}{2\sqrt{2}}
\end{eqnarray}\)

今度は\(\,\mathrm{△HIJ}\,\)を抜き出すと直角三角形です。
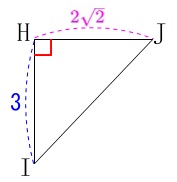三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{IJ}&=&\sqrt{\mathrm{HJ^2+HI^2}}\\
&=&\sqrt{(2\sqrt{2})^2+3^2}\\
&=&\sqrt{8+9}\\
&=&\underline{　\sqrt{17}　\mathrm{cm}}
\end{eqnarray}\)