秋田県公立高校入試2020年(令和2年)度の数学の問題と解説

秋田県で行われた公立高校入試2020年(令和2年)度の数学の問題と解説です。
秋田県立高校の入試では学校指定の問題があるので注意が必要ですが、解答時間は十分にあります。
最後に選択問題もありますが基本通り手を動かせば差のある問題ではありません。

平均点は2019年度より少し下がったとはいえ、基本から標準的な問題です。
※
秋田県の得点分布は受験者総数の\(\,8\,\)％を抽出したデータです。

秋田県公立高校入試2020年(令和2年)度の数学の問題

⇒　令和2年度秋田県立高校入試数学の問題

学校が指定する問題があるので、受験の際は学校から指示された問題を間違いなく解いてください。

秋田県公立高校入試2020年(令和2年)度の数学の解説

学校別に選択する問題があって少し多めになるので、
チャチャっと解説していきます。

第１問基本から標準までの小問集合

\(\,\large{1}\,\)

\(\,15\,\)問の中から学校が指示する\(\,8\,\)問を選びます。

(1)
　\(\hspace{10pt}1+\color{red}{(-0.2)\times 2}\\
=1-0.4\\
=\underline{　0.6　}\)

計算順序を間違えないようにしましょう。

(2)
　\(\hspace{10pt}\displaystyle \frac{6}{\sqrt{2}}\\
\displaystyle =\frac{6\color{red}{\times \sqrt{2}}}{\sqrt{2}\color{red}{\times \sqrt{2}}}\\
\displaystyle =\frac{6\sqrt{2}}{2}\\
=\underline{　3\sqrt{2}　}\)

ていねいに有理化しておきました。

(3)
代入は求値式（与式）を簡単にしてからです。

　\(\hspace{10pt}3(a-2b)-5(3a-b)\\
=3a-6b-15a+5b\\
=-12a-b\\
\displaystyle =-12\times \left(\frac{1}{2}\right)-(3)\\
=-6-3\\
=\underline{　-9　}\)

直接代入しても間違いではありませんが、遅いです。

(4)
日本語を不等式にしますが、
数量を文字式に変えることからですね。

　\(\,1\,\)個\(\,a\,\mathrm{kg}\,\)を\(\,3\,\)個は\(\,3a\,\mathrm{kg}\,\)
　\(\,1\,\)個\(\,b\,\mathrm{kg}\,\)を\(\,2\,\)個は\(\,2b\,\mathrm{kg}\,\)
合わせると
　\(\hspace{4pt}(\,3a+2b\,)\,\mathrm{kg}\,\)
これが\(\,20\,\mathrm{kg}\,\)以上なので
　\(\hspace{10pt}\underline{　3a+2b\,≧\,20　}\)

(5)
　\(\begin{eqnarray}\displaystyle
\frac{2x+4}{3}&=&4\\
2x+4&=&12\\
2x&=&8\\
x&=&\underline{　4　}
\end{eqnarray}\)

方程式を解くときの基本は\(\,(左辺)＝0\,\)とすることですが、
\(\,1\,\)次方程式は左辺に\(\,x\,\)の項、右辺に定数を移項すると早いです。

分数の方程式では分母を最初に無くすともっと早いです。

(6)
連立方程式を解くときは一文字消去ですね。
\(\,x\,\)を代入法で消しましょう。

　\(\begin{cases}
\hspace{4pt} 2x-3y=-5　･･･①\\
\hspace{4pt} x=-5y+4　･･･②
\end{cases}\)

②を①に代入します。

　\(\begin{eqnarray}\displaystyle
2(-5y+4)-3y&=&-5\\
-10y+8-3y&=&-5\\
-13y&=&-13\\
y&=&1
\end{eqnarray}\)

これを①にもどす（代入し直す）と
　\(\begin{eqnarray}\displaystyle
x&=&-5(1)+4\\
&=&-1
\end{eqnarray}\)

よって、
　\(\hspace{10pt}\underline{　x=-1\,,\,y=1　}\)

(7)
「方程式の解」とは、「方程式を成立させる値」のことです。
解の1つが\(\,-1\,\)なので方程式に代入しましょう。

　\(\begin{eqnarray}
(-1)^2-2a(-1)+3&=&0\\
1+2a+3&=&0\\
2a&=&-4\\
a&=&\color{red}{-2}
\end{eqnarray}\)

これを方程式にもどすと
　\(\begin{eqnarray}
x^2-2(\color{red}{-2})x+3&=&0\\
x^2+4x+3&=&0\\
(x+1)(x+3)&=&0\\
x&=&-1\,,\,-3
\end{eqnarray}\)

よって、もう一つの解は
　\(\hspace{10pt}\underline{　x=-3　}\)

\(\,2\,\)次方程式の\(\,x^2\,\)の係数が\(\,1\,\)なので、
　2つの解の積が定数項の\(\,3\,\)になる。
ということから\(\,-3\,\)とすぐに求まりますが、
「方程式の解とは？」という定義重視で解いていきましょう。

(8)
平均でも速さは道のりを時間で割ります。

片道\(\,a\,\mathrm{m}\,\)だから往復では\(\,\color{red}{2a}\,\mathrm{m}\,\)となるので、
往復でかかる時間を求めておきましょう。

往路（行き）では
　\(\hspace{4pt}\displaystyle \frac{a}{60}　分\)
復路（帰り）では
　\(\hspace{4pt}\displaystyle \frac{a}{90}　分\)
かかっているので往復で
　\(\hspace{10pt}\displaystyle \frac{a}{60}+\frac{a}{90}\\
\displaystyle =\frac{3a+2a}{180}\\
\displaystyle =\frac{5a}{180}\\
\displaystyle =\color{blue}{\frac{a}{36}}　分\)
かかっています。

よって、往復の平均の速さは毎分
　\(\hspace{10pt}\displaystyle \color{red}{2a}\div \color{blue}{\frac{a}{36}}\\
\displaystyle =2a\times \frac{36}{a}\\
=\underline{　72　\mathrm{m}}\)

行きの速さが\(\,60\,\)、帰りが\(\,90\,\)だから平均は中間の\(\,75\,\)としないようにしましょう。
道のりが一定だとするとき、
時間を求めるには速さは分母になる数なので、
逆数の中間が、速さの平均の逆数になります。
　\(\hspace{10pt}\displaystyle \left(\frac{1}{60}+\frac{1}{90}\right)\div 2\\
\displaystyle =\frac{3+2}{180}\times \frac{1}{2}\\
\displaystyle =\frac{1}{72}\)
似たような計算は理科の抵抗値の計算で見たことあるでしょう。
けど、忘れて良いです。

ただし、道のり、速さ、時間は計算して確実に求めましょう。

(9)
逆が正しいものを選びます。

逆とは、仮定と結論を入れかえたもののことです。

答え　\(\,\underline{　ア　}\,\)

内角がすべて等しければ（すべて\(\,60°。\,\)）ならば、正三角形である。

イ、ウ、エの逆は成り立ちません。
1つでも良いので成り立たない例を探し出せば良いです。
イ　ひし形で対角線の長さが違う形
ウ　\(\,x=4.5\,\)
エ　\(\,x=-1\,\)

(10)
ルートの付いた数が整数になる自然数の個数を求めます。
\(\,n\,\)を整数とすると
　\(\hspace{4pt}\displaystyle \sqrt{120+a^2}=n\)

左辺は正の平方根なので\(\,n\,\)は正の整数です。
両辺正なので平方しても成り立つので平方します。

　\(\hspace{4pt}120+a^2=n^2\)

変形すると
　\(\begin{eqnarray}
120&=&n^2-a^2\\
120&=&(n-a)(n+a)
\end{eqnarray}\)

このとき2つの数\(\,(n-a)\,\)と\(\,(n+a)\,\)は正の数で、
\(\,2\,\)つの数の和を\(\,2\,\)で割ると
　\(\hspace{4pt}\displaystyle \frac{(n-a)+(n+a)}{2}=n　(整数)\)
となります。

これは\(\,(n-a)\,\)と\(\,(n+a)\,\)の和が偶数であることを意味します。

積が\(\,120\,\)になる組み合わせは
　\(\,1\times 120\,\)
　\(\,2\times 60\,\)
　\(\,3\times 40\,\)
　\(\,4\times 30\,\)
　\(\,5\times 24\,\)
　\(\,6\times 20\,\)
　\(\,8\times 15\,\)
　\(\,10\times 12\,\)
後は逆になるだけなので組み合わせとしてはこれだけです。

この組み合わせで和が偶数になるのは
　\(\,2\times 60\,\)
　\(\,4\times 30\,\)
　\(\,6\times 20\,\)
　\(\,10\times 12\,\)
の4つです。

これは正である条件に適しています。

答え　\(\,\underline{　4　個}\,\)

※
この問題は具体的に求めなくて良いのですが、
\(\,n\,\)は2つの数の中間の数です。
足して\(\,2\,\)で割れば求まります。
\(\,a\,\)は大きい方から小さい方を引いて\(\,2\,\)で割れば求まります。
　\(\hspace{4pt}\displaystyle \frac{(n+a)-(n-a)}{2}=a\)

この問題は高校の「整数」でやり直すことになりますが、
　「\(n-a\,,\,n+a\,\)は奇遇が一致する。」
とかっこいい言い方をしますので、覚えておくと良いです。

ちょっと話がずれてしまいますが、
　\(\hspace{4pt}\sqrt{120+a^2}\)
が整数になる自然数\(\,a\,\)は大きな数にしていけばいくらでもありそうなのに、
　4つしかない。
小学校の頃から慣れ親しんだ整数の奥の深さを高校で感じて下さい。
（高校入試までは、調べ尽くす、で良いです。笑）

(11)
平行線と角度です。
　\(\,\ell\,\)　∥　\(\,m\,\)
なので同位角は等しくなります。
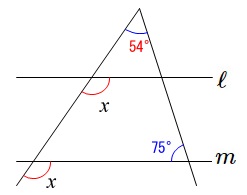よって、
　\(\begin{eqnarray}
x&=&\color{red}{54^{\circ}}+\color{blue}{75^{\circ}}\\
&=&\underline{　129^{\circ}　}
\end{eqnarray}\)
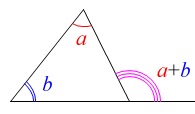三角形の1つの外角は、他の2つの内角の和です。

(12)
多角形の内角を求めます。

内角の和から計算しても求められますが、
「多角形の外角の和はつねに\(\,360^{\circ}\,\)」
を利用しましょう。

分かっている4つの外角の和は
　\(\hspace{10pt}55^{\circ}+115^{\circ}+65^{\circ}+79^{\circ}\\
=314^{\circ}\)
なので残りの外角は
　\(\hspace{10pt}360^{\circ}-314^{\circ}\\
=46^{\circ}\)
よって、
　\(\begin{eqnarray}
x&=&180^{\circ}-46^{\circ}\\
&=&\underline{　134^{\circ}　}
\end{eqnarray}\)

図に自分で書き込みながら進めてください。

(13)
ねじれの位置とは、
　「平行でもなく交わりもしない。」
ことです。
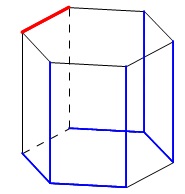本数だけなので記号は省きました。

答え　\(\,\underline{　8　本}\,\)
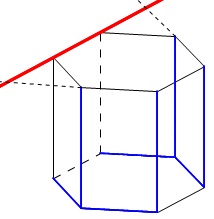延長して交わるものはねじれの位置とはいいません。

(14)
体積を求めるので高さを先に出しておきましょう。
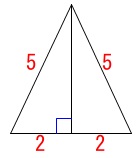三平方の定理から高さを\(\,h\,\)とすると、
　\(\begin{eqnarray}\displaystyle
h&=&\sqrt{5^2-2^2}\\
&=&\sqrt{21}
\end{eqnarray}\)

また底面積\(\,S\,\)は
　\(\hspace{10pt}S=\pi\,(2^2)=4\,\pi\)

よって、求める円すいの体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times S\times h\\
&=&\frac{1}{3}\times 4\,\pi\times \sqrt{21}\\
&=&\underline{　\frac{4\sqrt{21}}{3}\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

(15)
体積比です。
線分比があるので長さは必要ありません。

条件
　\(\,\mathrm{P,Q}\,\)は\(\,\mathrm{BC,BD}\,\)の中点
　\(\,\mathrm{AR:RB=1:4}\,\)
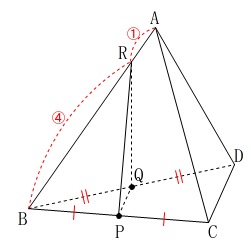三角錐\(\,\mathrm{A-BCD}\,\)と三角錐\(\,\mathrm{R-BPQ}\,\)において
底面は\(\,\mathrm{△BCD}\,\)と\(\,\mathrm{△BPR}\,\)が相似で
　相似比\(\,2:1\,\)
なので
　面積比は\(\,2^2:1^1=\color{magenta}{4}:\color{magenta}{1}\,\)

また、高さの比は\(\,\mathrm{AR:RB=1:4}\,\)なので
　\(\mathrm{AB:RB}=5:4\)
だから高さの比も　\(\hspace{10pt}\color{blue}{⑤}:\color{blue}{④}\)
よって、体積を\(\,\mathrm{[R-BPQ]}\,\)などと表すと
　\(\begin{eqnarray}\displaystyle
\mathrm{[R-BPQ]}&=&\mathrm{[A-BCD]}\times \frac{1}{4}\times \frac{4}{5}\\
&=&\frac{1}{5}\times \mathrm{[A-BCD]}\\
\mathrm{[A-BCD]}&=&5\times \mathrm{[R-BPQ]}
\end{eqnarray}\)

答え　\(\,\underline{　5　倍}\,\)

どちらも錐体なので\(\,\displaystyle \frac{1}{3}\,\)とか必要ないです。

第２問関数と作図と面積比

\(\,\large{2}\,\)

反比例のグラフと放物線の性質です。

(1)
関数\(\displaystyle \,y=\frac{3}{x}\,\)について言えることを選びます。
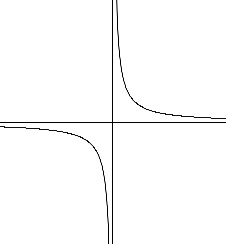\(\,x＞0\,\)の範囲においても、\(\,x＜0\,\)の範囲においても
\(\,x\,\)が増加すると、（右に移動すると）
\(\,y\,\)はつねに減少している。（下に移動する）

答え　\(\,\underline{　イ　,　エ　}\,\)

(2)
関数が2つありますが、同時に見ることはありません。

\(\,㋐\,\)\(\,y=ax^2\,\)
\(\,㋑\,\)\(\displaystyle \,y=-\frac{1}{2}x^2\,\)

条件
　\(\,\mathrm{P,Q}\,\)は\(\,㋐\,\)上の点。
　\(\,\mathrm{P}\,(\,6\,,\,9\,)\,\)
　\(\,\mathrm{Q}\,(\,-2\,,\,b\,)\,\)

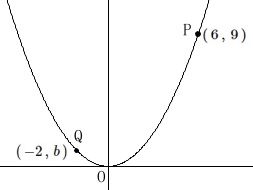
①
点\(\,\mathrm{Q}\,\)の\(\,y\,\)座標\(\,b\,\)を求めます。

点\(\,\mathrm{P}\,(\,6\,,\,9\,)\,\)が\(\,㋐\,\)上の点なので
　\(\begin{eqnarray}\displaystyle
9&=&a\times (6)^2\\
&=&36\,a\\
a&=&\frac{1}{4}
\end{eqnarray}\)
このことから関数\(\,㋐\,\)は
　\(\hspace{10pt}\displaystyle y=\frac{1}{4}x^2\)
と比例定数が定まります。
点\(\,\mathrm{Q}\,(\,-2\,,\,b\,)\)も\(\,㋐\,\)上の点なので
　\(\begin{eqnarray}\displaystyle
b&=&\frac{1}{4}\times (-2)^2\\
&=&\underline{　1　}
\end{eqnarray}\)

②
関数\(\displaystyle \,y=-\frac{1}{2}x^2\,\)は下に開いた（上に凸な）グラフです。
　\(\,x\,\)の変域\(\,c\,≦\,x\,≦\,2\,\)
のとき
　\(\,y\,\)の変域\(\,-8\,≦\,y\,≦\,d\,\)
最大値は\(\,x=0\,\)のとき\(\,y=0\,\)なので
　\(\,\underline{　d=0　}\,\)

また、最小値は\(\,-8\,\)なのでこのときの\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle
-8&=&-\frac{1}{2}x^2\\
16&=&x^2\\
x&=&\pm -4
\end{eqnarray}\)

\(\,x\,\)の変域は\(\,c\,≦\,x\,≦\,2\,\)なので
　\(\hspace{10pt}\underline{　c=-4　}\)

(3)
点を時計回りに\(\,45°\,\)回転移動させた点の作図です。

\(\,45°\,\)は\(\,90°\,\)の半分なので点\(\,\mathrm{O}\,\)を通る垂線を引いて、
角の二等分線を引けば終わりです。
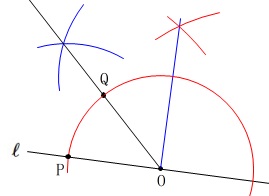\(\,\mathrm{OP}\,\)を半径に円を描くと点\(\,\mathrm{Q}\,\)はその円上にあるので、
点\(\,\mathrm{O}\,\)を通る垂線を引くときから利用すれば良いです。

(4)
平行四辺形の面積と内部にある三角形の面積比を求めます。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{CE:ED=1:2}\,\)
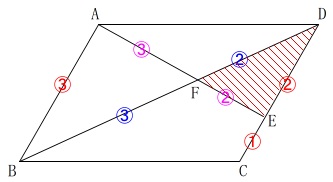\(\,\mathrm{△ABF}\,\)∽\(\,\mathrm{△EDF}\,\)
で、相似比が\(\,3:2\,\)なので、
\(\,\mathrm{△BCD}\,\)が平行四辺形\(\,\mathrm{ABCD}\,\)の面積\(\,\color{red}{S}\,\)の半分であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△DFE}&=&\color{red}{S}\times \frac{1}{2}\times \color{blue}{\frac{2}{5}}\times \color{red}{\frac{2}{3}}\\
&=&\frac{2}{15}\times \color{red}{S}
\end{eqnarray}\)

よって、\(\displaystyle \underline{　\frac{2}{15}　倍}\)

このようにすぐ出てくるのですが、少し説明しておきます。
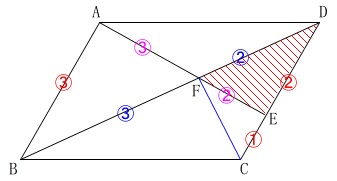\(\,\mathrm{CF}\,\)を結ぶと底辺\(\,\mathrm{BD}\,\)を\(\,\color{blue}{3:2}\,\)に分けているので
　\(\hspace{10pt}\displaystyle \mathrm{△CFD}=\color{blue}{\frac{2}{5}}\times\mathrm{ △BCD}\)
また、\(\,\mathrm{E}\,\)は\(\,\mathrm{DC}\,\)を\(\,\color{red}{2:1}\,\)に分けているので
　\(\hspace{10pt}\displaystyle \mathrm{△DFE}=\color{red}{\frac{2}{3}}\times \mathrm{△CFD}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△DFE}&=&\color{blue}{\frac{2}{3}}\times \color{red}{\frac{2}{5}}\times \mathrm{△BCD}\\
&=&\frac{4}{15}\times \mathrm{△BCD}
\end{eqnarray}\)
ここで
　\(\,\mathrm{△BCD}=\frac{1}{2}\times \color{red}{S}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△DFE}&=&\frac{4}{15}\times \frac{1}{2}\times \color{red}{S}\\
&=&\frac{2}{15}\times \color{red}{S}
\end{eqnarray}\)

また、\(\,\mathrm{E}\,\)を通り\(\,\mathrm{AD}\,\)に平行な線を引いて分割しても出てきます。
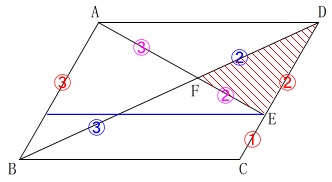やってみてください。（自分で）

第３問１次関数

加湿器のタンクの水の水量変化を見る\(\,1\,\)次関数の問題です。

加湿器の性能（条件）
　運転方法は強、中、弱の3段階
　タンクの容量は\(\,4000\,\mathrm{mL}\,\)
　強で\(\,4\,\)時間で空になる。
　中で\(\,5\,\)時間で空になる。
　弱で\(\,8\,\)時間で空になる。
　使い始めてからの時間を\(\,x\,\)、
　タンクの水の量を\(\,y\,\)とする。

\(\,1\,\)時間あたりの水の使用量を出しておきます。
　強：\(\,1000\,\mathrm{mL}\,\)
　中：\(800\,\mathrm{mL}\,\)
　弱：\(500\,\mathrm{mL}\,\)

(1)
強運転で\(\,2\,\)時間、弱運転で\(\,4\,\)時間使って空になったことになります。

①
先に出しておきましたが、
\(\,4\,\)時間で\(\,4000\,\mathrm{mL}\,\)を空にするので、
\(\,1\,\)時間あたり
　\(\hspace{10pt}\displaystyle \frac{4000}{4}=\underline{　1000　}\,\mathrm{mL}\)
減少します。

②
強運転\(\,2\,\)時間で
　\(\hspace{4pt}1000\times 2=2000\,mL\)
弱運転で\(\,4\,\)時間
　\(\hspace{4pt}500\times 4=2000\,mL\)
で使い切っています。
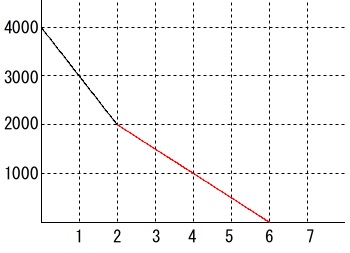関数を\(\,1\,\)次関数と見なし直線でつなげば良いです。

(2)
中運転と弱運転で\(\,7\,\)時間後にタンクがなったとき、
切り換えたのは何時間何分後かを\(\,1\,\)次関数を使って求めます。

方程式で良いのですがここでは、
\(\,1\,\)次関数にしてから交点で求めます。

①
中運転だけで使用する場合の直線は
　\(\,\mathrm{P}\,(\,0\,,\,4000\,)\,\)
　\(\,\mathrm{Q}\,(\,5\,,\,0\,)\,\)
を通る。
直線\(\,\mathrm{PQ}\,\)は
　\(\hspace{10pt}y=-800x+4000\)

\(\,7\,\)時間でタンクが空になるとき
　\(\,\mathrm{R}\,(\,7\,,\,0\,)\,\)
を通り、
　弱運転だと\(\,1\,\)時間で\(\,500\,\mathrm{mL}\,\)減るので、
　\(\,2\,\)時間前には\(\,1000\,\mathrm{mL}\,\)残っているはずだから
　\(\,\mathrm{S}\,(\,5\,,\,1000\,)\,\)
を通っている。
直線\(\,\mathrm{RS}\,\)は
　\(\hspace{10pt}y=-500x+3500\)
のグラフになることを説明してあります。

このグラフはつながらなくてはならないので、
運転を切り換えた時間は
　「直線\(\,\mathrm{PQ}\,\)と直線\(\,\mathrm{SR}\,\)の交点の\(\,x\,\)座標」
を読み取ると分かります。
これが\(\color{black}{\fbox{　b　}}\)の答えです。

②
すでに求めています。
直線\(\,\mathrm{PQ}\,\)の式は
　\(\hspace{10pt}y=\underline{　-800x+4000　}\)

直線\(\,\mathrm{RS}\,\)の式は
　\(\hspace{10pt}y=\underline{　-500x+3500　}\)

これらを連立すると
　\(\begin{eqnarray}\displaystyle
-800x+4000&=&-500x+3500\\
-300x&=&-500\\
x&=&\frac{5}{3}　(時間)
\end{eqnarray}\)
よって、
　\(\,\underline{　1　}\,\)時間\(\,\underline{　40　}\,\)分後

※
　\(\displaystyle \frac{5}{3}=1+\frac{2}{3}\)
で\(\,1\,\)時間は\(\,60\,\)分だから\(\displaystyle \frac{2}{3}\)時間は
　\(\displaystyle \frac{2}{3}\times 60=40　(分)\)です。

方程式で解けば、
　中運転で使った時間を\(\,x\,\)時間とすると、
　弱運転で使った時間は\(\,(\,7-x\,)\,\)時間となり、
　合計で\(\,4000\,\mathrm{mL}\,\)の水を使い切ったことになる。
なので
　\(\begin{eqnarray}\displaystyle
800x+500(7-x)&=&4000\\
300x&=&500\\
x&=&\frac{5}{3}
\end{eqnarray}\)

ここでは\(\,1\,\)次関数のグラフの交点を求めることと、
\(\,1\,\)次方程式を解くことは同じことだというのを示したかったのでしょう。

\(\,2\,\)本の直線が交わる時点が切り換えた時間というのはわかりますが、
直線\(\,\mathrm{RS}\,\)を求めてつなぎに行くというのは面白い発想ですよね。

第４問データの活用と確率

\(\,\large{4}\,\)

データの活用の代表値と確率の問題です。

(1)
度数分布表があります。

\(\,\mathrm{A}\,\)さんと\(\,\mathrm{B}\,\)さんのどちらが速く走れそうか、
\(\,100\,\mathrm{m}\,\)走の記録の回数を見ていきます。
　\(\begin{array}{|c|c|c|} \hline
　階級　 &\,\mathrm{A}(回)\,&\,\mathrm{B}(回)\,\\ \hline
14.1～14.3 & 4 & 2 \\ \hline
14.3～14.5 & 0 & 4 \\ \hline
14.5～14.7 & 2 & 0 \\ \hline
14.7～14.9 & 1 & 1 \\ \hline
14.9～15.1 & 3 & 3 \\ \hline
計 & 10 & 10 \\ \hline
\end{array}\)
計算しなくて良いですが平均値は同じです。

最頻値で見ると
　\(\,\mathrm{A}\,\)さんの最頻値は\(\,14.2\,\)秒
　\(\,\mathrm{B}\,\)さんの最頻値は\(\,14.4\,\)秒
なので
　\(\,\mathrm{A}\,\)さんの最頻値の方が小さい
ので、最頻値で見ると\(\,\mathrm{A}\,\)さんの方が速く走れるといえる。

度数分布表での最頻値は
　度数の一番多いの階級の真ん中の値（階級値）
になります。

例えば、\(\,\mathrm{A}\,\)さんの場合度数が一番多いのは、
　\(\,14.1\,\)秒以上\(\,14.3\,\)秒未満の階級
の度数\(\,4\,\)が一番多いので、
　\(\displaystyle \frac{14.1+14.3}{2}=14.2　秒\)
となります。

答え　ア　\(\,\underline{　14.2　}\,\)　イ　\(\,\underline{　14.4　}\,\)　ウ　\(\,\underline{　\mathrm{A}\,さん　}\,\)

(2)
大小2つのさいころの確率です。

　大きいさいころの出た目を\(\,\color{red}{a}\,\)
　小さいさいころの出た目を\(\,\color{blue}{b}\,\)
とします。

①
　積\(\,\color{red}{a}\,\color{blue}{b}\,\)が\(\,4\,\)の倍数になる確率
を求めます。

\(\,36\,\)通りしかありませんので樹形図で良いです。
2つのさいころの場合は表をおすすめしていますがどちらでも構いません。

積を書き込んでも良いですが、
\(\,4\,\)の倍数になるところに\(\,\color{magenta}{●}\,\)をします。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4 }& \color{blue}{5} & \color{blue}{6}\\ \hline
\color{red}{1} & & & & \color{magenta}{●} & & \\ \hline
\color{red}{2} & & \color{magenta}{●} & & \color{magenta}{●} & & \color{magenta}{●}\\ \hline
\color{red}{3} & & & & \color{magenta}{●} & & \\ \hline
\color{red}{4} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●}\\ \hline
\color{red}{5} & & & & \color{magenta}{●} & & \\ \hline
\color{red}{6} & & \color{magenta}{●} & & \color{magenta}{●} & & \color{magenta}{●}\\ \hline
\end{array}\)
\(\,4\,\)をかけるか、偶数どうしの積で\(\,4\,\)の倍数になりますが、
数えた方が早いです。

答え　\(\displaystyle \frac{15}{36}=\underline{　\frac{5}{12}　}\)

②
\(\,10a+b\,\)が素数になる確率を求めます。

変形してもムダです。
素数は簡単に式にできる数ではありません。

調べ尽くしましょう。
　\(\,a=1\,\)のとき十の位が\(\,1\,\)なので
　\(\hspace{10pt}11\,,\,13\,,\,17\,,\,19\)
が素数ですが、
さいころで\(\,7,9\,\)は出ないので\(\,17,19\,\)はありません。

同じように調べると
　\(\,a=1\,\)のとき\(\,b=1,3\,\)
　\(\,a=2\,\)のとき\(\,b=3\,\)
　\(\,a=3\,\)のとき\(\,b=1\,\)
　\(\,a=4\,\)のとき\(\,b=1,3\,\)
　\(\,a=5\,\)のとき\(\,b=3\,\)
　\(\,a=6\,\)のとき\(\,b=1\,\)
が素数になるときで計\(\,8\,\)通りあります。

答え　\(\displaystyle \frac{8}{36}=\underline{　\frac{2}{9}　}\)

第５問弧と角の比例関係を利用した証明と面積比

\(\,\large{5}\,\)

\(\,\mathrm{\large{Ⅰ}}\,\)と\(\,\mathrm{\large{Ⅱ}}\,\)があります。
学校によって指示される問題が変わりますので間違えないようにしましょう。

第５問選択問題１

\(\,\mathrm{\large{Ⅰ}}\,\)

図\(\,1\,\)のような半円があります。

条件
　\(\,\mathrm{AB}\,\)は直径で\(\,\mathrm{AB=8}\,\)
　\(\,\mathrm{C,D,E}\,\)は\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AB}}}\,\)を\(\,4\,\)等分する点
（単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。）
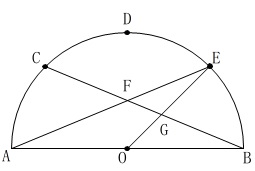条件は図に書き込むと分かり易くなります。

先ずは自分でやってみましょう。
見えてくることがたくさん出てきます。

(1)
\(\,\mathrm{∠AOG}\,\)の大きさを求めます。
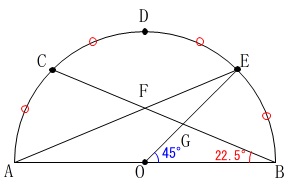\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BE}}}\,\)は半円の\(\,4\,\)等分になるので、
中心角は
　\(\displaystyle \,\mathrm{∠BOE=\frac{180^{\circ}}{8}=\color{blue}{45^{\circ}}}\,\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AOG}&=&180^{\circ}-\color{blue}{45^{\circ}}\\
&=&\underline{　135^{\circ}　}
\end{eqnarray}\)

(2)
\(\,\mathrm{△FAB}\,\)が二等辺三角形であることを証明します。
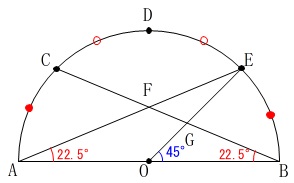\(\,\mathrm{C,D,E}\,\)は\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AB}}}\,\)を\(\,4\,\)等分する点なので、
　\(\hspace{10pt}\,\mathrm{\stackrel{\large{\frown}}{\mbox{AC}}\,=\,\stackrel{\large{\frown}}{\mbox{BE}}}\,\)
同一長の弧に対する円周角は等しいので、
　\(\hspace{10pt}\mathrm{∠ABC=∠BAE}\,(=22.5^{\circ})\)
\(\,2\,\)角が等しいので
　\(\,\mathrm{△FAB}\,\)は二等辺三角形である。

定理を使った証明通りなので説明は必要ないでしょう。

(3)
条件はそのままですが線分が書き込まれ、
\(\,\mathrm{△ACE}\,\)の面積を求めます。
長さは直径の\(\,\mathrm{AB=8}\,\)しか分かっていませんので、
半径が\(\,4\,\)であることからはじめましょう。
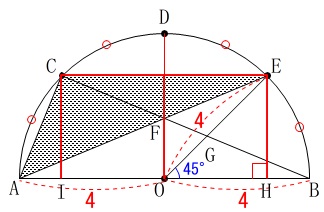\(\,\mathrm{C,E}\,\)から\(\,\mathrm{AB}\,\)に垂線を下ろすと、
\(\,\mathrm{∠BOE=45^{\circ}}\,\)なので正方形が2つできます。

　\(\hspace{10pt}\mathrm{OE:EH}=\sqrt{2}:1\)
なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{OE:EH}&=&\sqrt{2}:1\\
4:\mathrm{EH}&=&\sqrt{2}:1\\
\sqrt{2}\times \mathrm{EH}&=&4\\
\mathrm{EH}&=&\frac{4}{\sqrt{2}}\\
&=&\color{blue}{2\sqrt{2}}
\end{eqnarray}\)
底辺を\(\,\mathrm{CE}\,\)、高さを\(\,\mathrm{EH}\,\)とすると、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACE}&=&\frac{1}{2}\times \mathrm{CE}\times \mathrm{EH}\\
&=&\frac{1}{2}\times 4\sqrt{2}\times 2\sqrt{2}\\
&=&\underline{　8　\mathrm{cm^2}}
\end{eqnarray}\)

第５問選択問題２

\(\,\mathrm{\large{Ⅱ}}\,\)

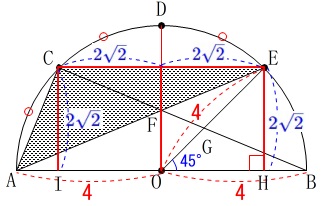
半円と半円の\(\,6\,\)等分点が与えられた図があります。

条件
　\(\,\mathrm{AB}\,\)は直径で\(\,\mathrm{AB=12}\,\)
　\(\,\mathrm{C,D,E,F,G}\,\)は\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AB}}}\,\)を\(\,6\,\)等分する点
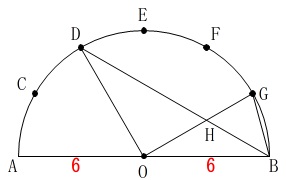半径は\(\,\color{red}{6}\,\)になります。

(1)
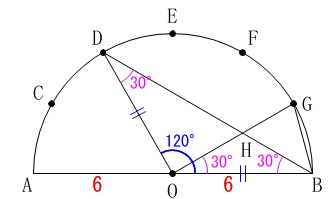
\(\,\mathrm{△HOB}\,\)が二等辺三角形であることを証明します。
半円の\(\,6\,\)等分点ということは、
円周の\(\,12\,\)等分点なので中心角が分かります。

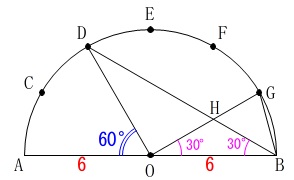
中心角は弧に比例するので仮定から
　\(\,\mathrm{∠AOD}=\color{blue}{60^{\circ}}\,\)
円周角の定理から
　\(\mathrm{∠ABD}=\color{magenta}{30^{\circ}}\)
また、\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BG}}}\,\)の中心角は
　\(\mathrm{∠BOG}=\color{magenta}{30^{\circ}}\)
よって、
　\(\mathrm{∠HBO=∠HOB}\)
\(\,2\,\)角が等しくなるので、
　\(\,\mathrm{△HOB}\,\)は二等辺三角形である。

または、

問題の条件（仮定）から
　\(\,\mathrm{∠BOD}=\color{blue}{120^{\circ}}\,\)
半径は等しいから\(\,\mathrm{△OBD}\,\)は二等辺三角形で、
　\(\,\mathrm{∠OBD=∠ODB}=\color{magenta}{30^{\circ}}\,\)
また、中心角は弧に比例するので
　\(\,\mathrm{∠BOG}=\color{magenta}{30^{\circ}}\,\)
よって、
　\(\mathrm{∠OBD=∠BOG}\)
つまり、
　\(\,\mathrm{∠HBO=∠HOB}\,\)
\(\,2\,\)角が等しいから\(\,\mathrm{△HOB}\,\)は二等辺三角形である。

中心角は弧の分割の割合から出していることを、
もう少し具体的な数値を証明の中に加えた方が減点されずに済むかもしれないですね。

いずれにしてもポイントは、
証明は図の中で済ませておくことです。

(2)
線分\(\,\mathrm{GH}\,\)の長さを求めます。
半径\(\,\mathrm{OG}\,\)は\(\,\color{red}{6}\,\)と分かっています。

　\(\hspace{10pt}\mathrm{GH=OG-OH}\)
なので\(\,\mathrm{OH}\,\)を求めることにします。

\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{DG}}}\,\)の中心角が\(\,90°\,\)であることから、
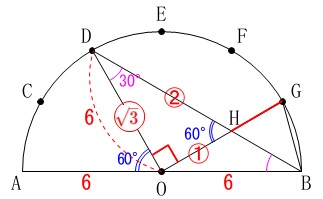\(\,\mathrm{△ODH}\,\)は直角三角形で\(\,\mathrm{∠ODH=30^{\circ}}\,\)なので三角定規です。
　\(\,\mathrm{OH:DH:OD=\color{red}{1}:\color{red}{2}:\color{red}{\sqrt{3}}}\,\)

半径\(\,\mathrm{OD=6}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{OH:OD}&=&1:\sqrt{3}\\
\mathrm{OH}:6&=&1:\sqrt{3}\\
\sqrt{3}\times \mathrm{OH}&=&6\\
\mathrm{OH}&=&2\sqrt{3}
\end{eqnarray}\)

よって、\(\,\mathrm{OG=\color{red}{6}}\,\)であることから
　\(\begin{eqnarray}\mathrm{GH}&=&\mathrm{OG-OH}\\
&=&\underline{　6-2\sqrt{3}　\mathrm{cm}}
\end{eqnarray}\)

\(\,\mathrm{H}\,\)から\(\,\mathrm{OB}\,\)に垂線を引いても三角定規ができるので、
\(\,\mathrm{OH}\,\)を求めることができます。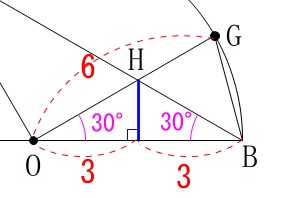何でも良いですよ。
思い立ったら突っ走る、で十分な条件、時間はあります。

(3)
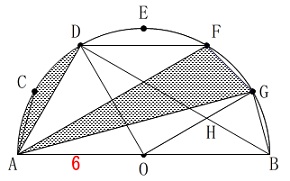
図\(\,2\,\)の影の部分の面積を求めます。
　図\(\,2\,\)
正三角形を確認できるので、
部分的に面積を求めることもできます。

しかし、等積移動すれば扇形の面積として求めることができます。
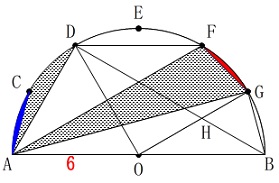中心角が同じであることから弦\(\,\mathrm{FG}\,\)と弧\(\,\mathrm{FG}\,\)で囲まれた部分の面積を、
弦\(\,\mathrm{AC}\,\)と弧\(\,\mathrm{AC}\,\)で囲まれた部分に移動します。
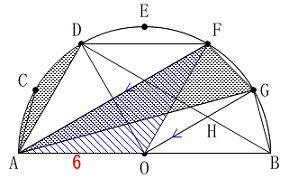
次に、中心角である\(\,\mathrm{∠GOB=30^{\circ}}\,\)と、
円周角\(\,\mathrm{∠BAF=30^{\circ}}\,\)が等しいことから、
　\(\,\mathrm{GO}\,\)∥\(\,\mathrm{FA}\,\)
なので、頂点\(\,\mathrm{G}\,\)を平行移動して
　\(\,\mathrm{△GAF=△OAF}\,\)
また、\(\,\mathrm{∠GOD=90^{\circ}}\,\)なので、
半径\(\,\mathrm{OD}\,\)と\(\,\mathrm{AF}\,\)の交点を\(\,\mathrm{K}\,\)とすると
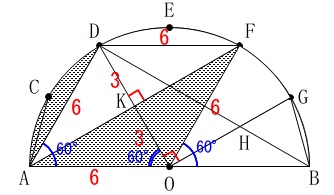半径や円周角から\(\,\mathrm{△OFK}\,\)≡\(\,\mathrm{△ADK}\,\)がいえるので、
（四角形\(\,\mathrm{OADF}\,\)はひし形です。）
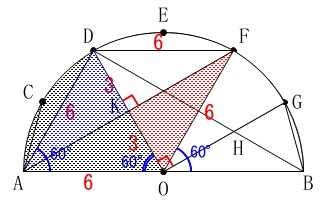求める面積\(\,S\,\)は、
　\(\begin{eqnarray}\displaystyle
S&=&\pi\,(6)^2\times \frac{60}{360}\\
&=&36\,\pi\times \frac{1}{6}\\
&=&\underline{　6\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)