青森県公立高校入試2020年（令和2年）度数学の問題と解説

青森県公立高校入試で2020年（令和2年）度に実施された数学の問題と解説です。
数学の平均点は前年より10点以上上がっていますが、
例年通り教科書の範囲から偏りなく出題される、基本重視の青森の公立入試問題です。

青森県公立高校入試2020年（令和2年）度数学の問題

※
青森県公立入試では\(\,2021\,\)年度の範囲は除外する部分はなく、教科書全般から出題されます。
ただし、生徒の授業受講時間を配慮して、基礎、基本的な問題で出題されます。

⇒　令和２年度青森県公立高校入試の数学問題

大問で\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであります。
試験時間は\(\,45\,\)分ですが十分でしょう。

青森県公立高校入試2020年（令和2年）度数学の解説

満点の人も多かった問題ですので解説は簡単に済ませます。

第１問基本小問集合

(1)式の計算問題が\(\,5\,\)題あります。

ア
　\(\hspace{10pt}-5-(-7)\\
=-5+7\\
=\underline{　2　}\)

イ
　\(\hspace{10pt}\displaystyle \left(\frac{1}{4}-\frac{2}{3}\right)\times 12\\
\displaystyle =\frac{1}{4}\times 12-\frac{2}{3}\times 12\\
\displaystyle =3-8\\
=\underline{　-5　}\)

（かっこ）の中は通分しても良いですが、
公約数をかけるので\(\,2\,\)行目は暗算でも良いです。

ウ
　\(\hspace{10pt}\displaystyle 4x\times \frac{2}{5}xy\div 2x^2\\
\displaystyle =\frac{4x\times 2xy}{5\times 2x^2}\\
\displaystyle =\underline{　\frac{4}{5}\,y　}\)

エ
　\(\hspace{10pt}(-2a+3)(2a+3)+9\\
=(3-2a)(3+2a)+9\\
=9-4a^2+9\\
=\underline{　18-4a^2　}\)

\(\,2\,\)行目は公式
　\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
が使いやすいように順序を変えただけです。

オ
　\(\hspace{10pt}\sqrt{24}\div \sqrt{8}-\sqrt{12}\\
=\sqrt{3}-2\sqrt{3}\\
=\underline{　-\sqrt{3}　}\)

ルートの中身は約分することになるので、
割り切れるときは割って良いです。

(2)
関係を等式で表します。

金額は
　\(\,100\,\)円硬貨\(\,a\,\)枚なので\(\,100\,a\,\)円
　\(\,50\,\)円硬貨\(\,b\,\)枚なので\(\,50\,b\,\)円
合計\(\,\color{red}{100\,a+50\,b}\,\)円あることになります。
これを\(\,10\,\)円硬貨にすると\(\,c\,\)枚になるので\(\,\color{blue}{10\,c}\,\)円

金額で等式にするか、硬貨の枚数で等式にするかで違います。

金額で等式にすると
　\(\underline{　100a+50b=10c　}\)

硬貨の枚数で等式にすると
　\(\,100a\,\)円は\(\,10\,\)円硬貨で\(\,10\,a\,\)枚
　\(\,50b\,\)円は\(\,10\,\)円硬貨で\(\,5\,b\,\)枚
なので
　\(\underline{　10a+5b=c　}\)

(3)
素因数分解です。
小さな素数からはじめると良いですよ。
　\(\hspace{10pt}\underline{2)150}\\
\hspace{10pt}\underline{3)\hspace{4pt}75}\\
\hspace{10pt}\underline{5)\hspace{4pt}25}\\
\hspace{26pt}5\)

　\(\hspace{4pt}150=\underline{　2\times 3\times 5^2　}\)

(4)
連立方程式を解く基本は一文字消去です。
ここでは代入法で\(\,y\,\)を消去します。
　\( \begin{cases}
\hspace{4pt} y=\color{blue}{4(x+2)}　･･･①\\
\hspace{4pt} 6x-y=-10　･･･②
\end{cases}\)

①を②の\(\,y\,\)に代入して
　\(\begin{eqnarray}\displaystyle
6x-\color{blue}{4(x+2)}&=&-10\\
6x-4x-8&=&-10\\
2x&=&-2\\
x&=&\color{red}{-1}
\end{eqnarray}\)

これを①にもどして
　\(\begin{eqnarray}\displaystyle
y&=&4(\color{red}{-1}+2)\\
&=&4
\end{eqnarray}\)

答え　\(\,\underline{　x=-1\,,\,y=4　}\,\)

(5)
関数\(\,\displaystyle y=\frac{a}{x}\,\)について適切でないものを選びます。
ここでは、比例定数は負です。
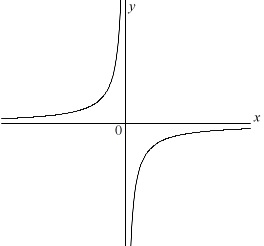ア、イ、ウは正しいです。

エの
　「\(\,x\,\)の値を大きくしていくと\(\,x\,\)軸に近づき、」
までは正しいですが、
\(\,x\,\)軸とは交わることはありません。

答え　\(\,\underline{　エ　}\,\)

(6)
標本調査は、比例式で良いです。
箱の中の白玉を\(\,x\,\)個とすると

　\(\,x\,\)個の白玉の中に\(\,100\,\)個の黒玉を入れて\(\,x+100\,\)個にした。
つまり、
　\(\,x+100\,\)個の中に\(\,100\,\)個の黒玉。

また、
　\(\,x+100\,\)個の中から\(\,34\,\)個取り出すと黒玉が\(\,4\,\)個だった。
つまり、
　\(\,34\,\)個の中に\(\,4\,\)個の黒玉があった。

よって、
　\(\begin{eqnarray}\displaystyle
x+100:100&=&34:4\\
4(x+100)&=&34\times 100\\
4x+400&=&3400\\
4x&=&3000\\
x&=&750
\end{eqnarray}\)

答え　\(\,\underline{およそ　750　個}\,\)

時計回りに比例計算すると
　\(\displaystyle \hspace{10pt}4\times \frac{(x+100)}{34}=100\)
となります。

(7)
角の大きさを求めます。

条件
　\(\,\ell\,\)∥\(\,m\,\)
　\(\,\mathrm{AB=AC}\,\)
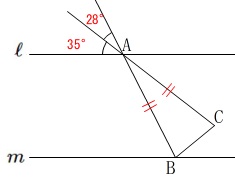うまい方法なんて必要ありません。
分かる角度を書き込んで行けば良いだけです。
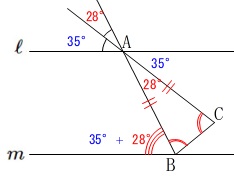平行線と二等辺三角形という条件があるので、
錯角と底角が分かります。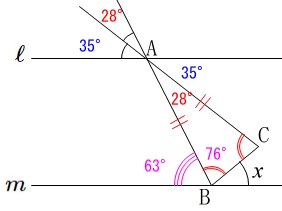
　\(\begin{eqnarray}\displaystyle
x&=&180^{\circ}-(63^{\circ}+76^{\circ})\\
&=&\underline{　41^{\circ}　}
\end{eqnarray}\)
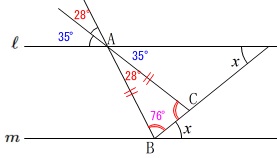\(\,\mathrm{BC}\,\)を延長して錯角を作るというのも2つの条件を使っているので良いですね。

(8)
半球の表面積です。
切り口の円を忘れないようにしましょう。

求める表面積を\(\,S\,\)とすると
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times 4\,\pi\,(6)^2+\pi\,(6)^2\\
&=&72\,\pi+36\,\pi\\
&=&\underline{　108\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)

覚えておかないと求められない公式なので書いておきます。
半径\(\,r\,\)の球の体積は
　\(\hspace{10pt}\displaystyle \color{red}{V=\frac{4}{3}\pi\,r^3}\)
表面積は
　\(\hspace{10pt}\color{red}{S=4\,\pi\,r^2}\)
です。

第２問文字式と確率

\(\color{black}{\fbox{2}}\)

文字式の関係式から整数を求める問題と、
2つのさいころを投げたときの確率の\(\,2\,\)問があります。

(1)
問題をまとめると
　\(a\,＜\,b\,＜\,c\,＜\,d\)
となる自然数があって、
　\(p=ab+cd+ac+bd\)
とするときそれぞれの条件に合う自然数を求めます。
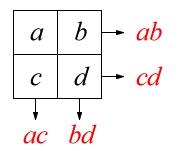図で見ると縦と横の積のそれぞれの和です。
（斜めはありません。）

\(\,a=2\,,\,b=3\,,\,c=7\,\)で
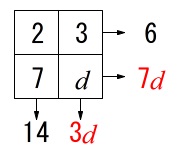\(\,p=150\,\)となるとき
　\(\begin{eqnarray}
6+7d+14+3d&=&150\\
10d&=&130\\
d&=&\color{red}{13}
\end{eqnarray}\)

\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　13　}\,\)

次に、\(\,a=3\,,\,d=9\,\)で
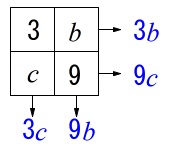p=168となるとき
　\(\begin{eqnarray}
3b+9c+3c+9b&=&168\\
\color{red}{12}(b+c)&=&168\\
b+c&=&\color{magenta}{14}
\end{eqnarray}\)

\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　12　}\,\)　\(\color{black}{\fbox{　ウ　}}\)　\(\,\underline{　14　}\,\)

ここで\(\,a=3\,,\,d=9\,\)なので、
\(a\,＜\,b\,＜\,c\,＜\,d\)だから
\(\,b\,\)と\(\,c\,\)は\(\,4,5,6,7,8\,\)のどれかです。

\(\,b+c=14\,\)を満たす自然数で、
かつ\(\,b\,＜\,c\,\)であるのは、
　\(\hspace{10pt}b=6\,,\,c=8\)
だけです。

\(\color{black}{\fbox{　エ　}}\)　\(\,\underline{　6　}\,\)　\(\color{black}{\fbox{　オ　}}\)　\(\,\underline{　8　}\,\)

(2)
円周が\(\,8\,\)と見たとき「え？」と思いましたが、
（円周率がないから）
正八角形でも同じ問題です。

条件
　円周上を\(\,8\,\)等分した点がある。
　\(\,\mathrm{P,Q}\,\)は円周上の1つの点\(\,\mathrm{A}\,\)から出発する。

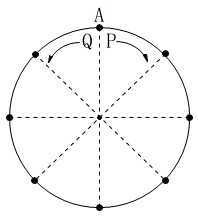
操作通りに\(\,\mathrm{P,Q}\,\)の動きを見ていきます。
さいころ2つなので\(\,36\,\)通りしかありません。

操作
　大小2つのさいころを投げる。
　大きいさいころの出た目の数を\(\,x\,\)
　小さいさいころの出た目の数を\(\,y\,\)
　\(\,\mathrm{P}\,\)は時計回りに\(\,x\,\)移動する。
　\(\,\mathrm{Q}\,\)は反時計回りに\(\,y\,\)移動する。
（単位の\(\,\mathrm{cm}\,\)は省略しています。）
　
ア
\(\,x=4\,,\,y=2\,\)となるときの\(\,\mathrm{∠PAQ}\,\)の大きさを求めます。　
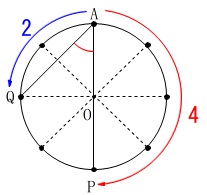計算するまでもありません。

答え　\(\,\underline{　45^{\circ}　}\,\)

イ
\(\,\mathrm{∠PAQ=90^{\circ}}\,\)となる確率です。

円周角が\(\,90^{\circ}\,\)になるときなので、
\(\,\mathrm{PQ}\,\)が円の直径になるときです。

樹形図でも表でも良いですよ。

ここでは\(\,\mathrm{PQ}\,\)が直径になる場合を調べつくします。

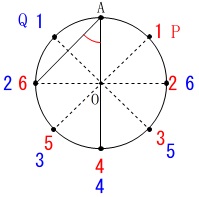
　\(\,x=\color{red}{1}\,\)のとき\(\,y=\color{blue}{3}\,\)
　\(\,x=\color{red}{2}\,\)のとき\(\,y=\color{blue}{2}\,\)
　\(\,x=\color{red}{3}\,\)のとき\(\,y=\color{blue}{1}\,\)
　\(\,x=\color{red}{4}\,\)のときなし
　\(\,x=\color{red}{5}\,\)のときなし
　\(\,x=\color{red}{6}\,\)のとき\(\,y=\color{blue}{6}\,\)

\(\,36\,\)通りのなかで\(\,4\,\)通りだけ\(\,\mathrm{PQ}\,\)が直径となる。

よって求める確率は
　\(\displaystyle \frac{4}{36}=\underline{　\frac{1}{9}　}\)

第３問図形総復習問題

\(\color{black}{\fbox{3}}\)

線分の長さ、回転体の体積、扇形の中心角を求める問題と、
相似の証明と面積比を求める図形総合問題です。
一つひとつは基本問題なのでどんどん進めます。

(1)
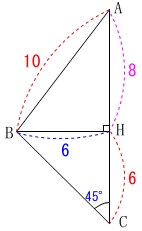
図が与えられています。

条件
　\(\,\mathrm{BH}\,\)⊥\(\,\mathrm{AC}\,\)
　\(\,\mathrm{AB=10}\,\)
　\(\,\mathrm{CH=6}\,\)
　\(\,\mathrm{∠BCH=45^{\circ}}\,\)
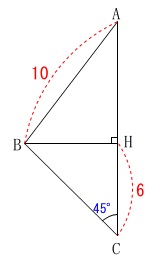分かるところから順に追えばすべてが分かります。

\(\,\mathrm{△CBH}\,\)は直角二等辺三角形なので
　\(\hspace{10pt}\mathrm{BH}=\color{blue}{6}\)
このとき\(\,\mathrm{△ABH}\,\)は\(\,3:4:5\,\)の直角三角形なので
　\(\hspace{10pt}\mathrm{AH}=\color{magenta}{8}\)
\(\,\mathrm{△ABH}\,\)の比を覚えていない人は、
三平方の定理を使えば\(\,\mathrm{AH}\,\)は簡単に出ます。

ア
\(\,\mathrm{AH}\,\)の長さを求めます。

\(\,\mathrm{BH=6}\,\)までは三角定規を利用したとして、
三平方の定理から
　\(\begin{eqnarray}
\mathrm{AH^2+BH^2}&=&\mathrm{AB^2}\\
\mathrm{AH^2}+6^2&=&10^2\\
\mathrm{AH^2}&=&10^2-6^2\\
&=&64\\
\mathrm{AH}&=&\pm 8
\end{eqnarray}\)

\(\,\mathrm{AH\,＞\,0}\,\)なので
　\(\hspace{10pt}\mathrm{AH}=\underline{　8　\mathrm{cm}}\)

イ
\(\,\mathrm{△ABC}\,\)を\(\,\mathrm{AC}\,\)を軸として\(\,1\,\)回転させた体積を求めます。
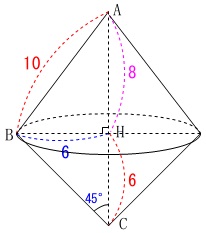底面が同じ円の2つの円すいです。

底面の円の面積\(\,S\,\)は半径\(\,6\,\)なので
　\(\hspace{10pt}S=36\,\pi\)

高さは\(\,\color{magenta}{8}+\color{red}{6}=14\,\)とできるので
求める体積を\(\,V\,\)とすると
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 36\,\pi\times 14\\
&=&\underline{　168\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

高さは\(\,8\,\)と\(\,6\,\)の円すいなので2つの円すいを計算して足しても良いですが、
底面の面積が同じなので高さ\(\,14\,\)の円すいと同じ体積になります。
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times S\times \mathrm{AH}+\frac{1}{3}\times S\times \mathrm{CH}\\
&=&\frac{1}{3}\times S\times (\mathrm{AH+CH})\\
&=&\frac{1}{3}\times S\times \mathrm{AC}\\
&=&\frac{1}{3}\times 36\,\pi\times 14\\
&=&\underline{　168\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

ウ
円すいの展開図における側面の扇形の中心角を求めます。
イの回転体の上の円すいです。

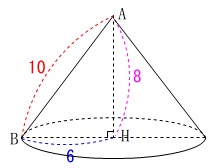
展開図を適当に書いて、
弧の長さを求めれば中心角は比例することを利用します。
底面の円周と扇形の弧の長さは同じです。
底面の半径は\(\,\color{blue}{6}\,\)なので円周は\(\,\color{magenta}{12\,\pi}\,\)

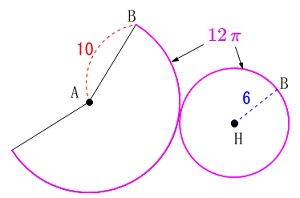
円すいの母線は扇形の半径\(\,10\,\)になるので、
母線を半径とする円周は\(\,\color{blue}{20\,\pi}\,\)となります。
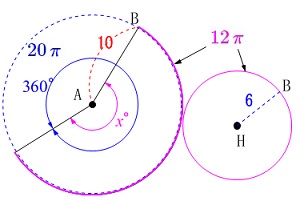これは中心角\(\,360°\,\)に対する弧と考えられるので
扇形の中心角\(\,x^{\circ}\,\)との比は
　\(\begin{eqnarray}\displaystyle
\color{blue}{360}:\color{magenta}{x}&=&\color{blue}{20\,\pi}:\color{magenta}{12\,\pi}\\
20x&=&12\times 360\\
x&=&216
\end{eqnarray}\)

答え　\(\,\underline{　216^{\circ}　}\,\)

比例計算なので
　\(\hspace{4pt}\displaystyle 360^{\circ}\times \frac{12\,\pi}{20\,\pi}=216^{\circ}\)
としても良いです。

(2)
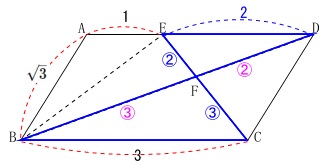
平行四辺形と分割する線分があります。

条件
　\(\,\mathrm{AB=\sqrt{3}}\,\)
　\(\,\mathrm{BC=3}\,\)
　\(\,\mathrm{AE=1}\,\)
（単位を\(\,\mathrm{cm}\,\)は省略します。）
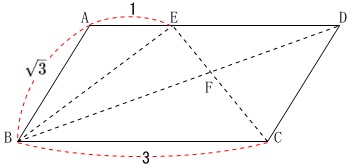これも分かることを追っていけばほとんど長さや長さの比が出ますが、
問題の順に見ていきましょう。

ア
\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△CBD}\,\)が相似であることを証明します。

四角形\(\,\mathrm{ABCD}\,\)は平行四辺形なので対辺と対角が等しいです。
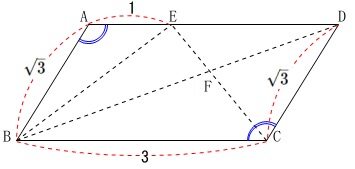問題は穴埋めなので記号の順番を合わせれば考えることが少ないですが、
簡単に示しておくと、
平行四辺形の対角は等しいから
　\(\,\mathrm{∠BAE=∠BCD}\,\)
また、対辺は等しくなるから
　\(\hspace{4pt}\mathrm{AB=DC}=\sqrt{3}\)
このとき
　\(\hspace{4pt}\mathrm{ＡＥ:ＣＤ}=1:\sqrt{3}\)
　\(\hspace{4pt}\mathrm{ＡＢ:ＣＢ}=\sqrt{3}:3=1:\sqrt{3}\)
となり、
　\(\,2\,\)組の辺の比とその間の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△CBD}\,\)

答え
　\(\color{black}{\fbox{　あ　}}\)　\(\,\underline{　\mathrm{∠BCD}　}\,\)
　\(\color{black}{\fbox{　い　}}\)　\(\,\underline{　\sqrt{3}　}\,\)
　\(\color{black}{\fbox{　う　}}\)　\(\,\underline{　\mathrm{CB}　}\,\)
　\(\color{black}{\fbox{　え　}}\)　\(\,\underline{　比　}\,\)

イ
\(\,\mathrm{△BCF}\,\)の面積が\(\,\mathrm{△ABE}\,\)の面積の何倍かを求めます。

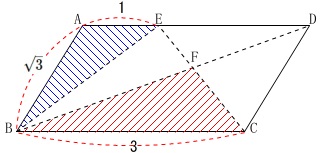
四角形\(\,\mathrm{ABCD}\,\)が平行四辺形なので、
　\(\,\mathrm{△BCF}\,\)∽\(\,\mathrm{△DEF}\,\)

また、\(\,\mathrm{AE=1,BC=3}\,\)であることから
　\(\,\mathrm{ED=2}\,\)
なので相似比は\(\,\mathrm{3：2}\,\)です。
実際の面積は出ないので比で見ていきますが、
全体を\(\,1\,\)とするのが一般的に通用する方法です。

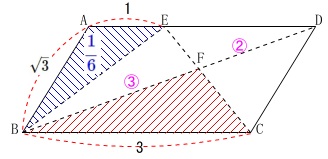
平行四辺形\(\,\mathrm{ABCD}\,\)を\(\,1\,\)とすると
　\(\displaystyle \,\mathrm{　\color{magenta}{△ABD}=\color{magenta}{△BCD}=\color{magenta}{\frac{1}{2}}}\,\)

\(\,\mathrm{AE:ED=1:2}\,\)なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&\frac{1}{1+2}\times \mathrm{\color{magenta}{△ABD}}\\
&=&\frac{1}{3}\times \color{magenta}{\frac{1}{2}}\\
&=&\color{blue}{\frac{1}{6}}
\end{eqnarray}\)
また、
　\(\,\mathrm{BF:FD=3:2}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCF}&=&\frac{3}{3+2}\times \mathrm{\color{magenta}{△BCD}}\\
&=&\frac{3}{5}\times \color{magenta}{\frac{1}{2}}\\
&=&\color{red}{\frac{3}{10}}
\end{eqnarray}\)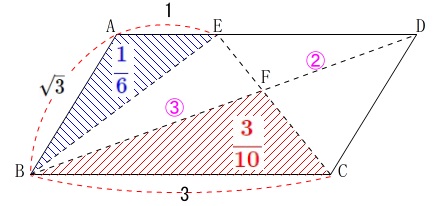よって、\(\,\mathrm{△BCF}\,\)の面積は\(\,\mathrm{△ABE}\,\)の
　\(\hspace{10pt}\displaystyle \color{red}{\frac{3}{10}}\div\color{blue}{ \frac{1}{6}}\\
\displaystyle =\frac{3}{10}\times \frac{6}{1}\\
\displaystyle =\underline{　\frac{9}{5}　倍}\)

どっちをどっちで割るかわかりにくいという人がいますが、
　「\(\,10\,\)は\(\,2\,\)の何倍か？」
というとき
　\(\hspace{4pt}10\div 2=5\)
とするのと同じで
　「\(\,a\,\)は\(\,b\,\)の何倍か？」
というときは
　\(\hspace{4pt}a\div b\)
で良いのです。

平行四辺形\(\,\mathrm{ABCD}\,\)全体を\(\,30\,\)とすると整数で進めることができますが、
最小公倍数を探すのに時間を費やすことが多いので、
全体を\(\,1\,\)とする方法に慣れると良いですよ。

第４問関数総復習問題

\(\color{black}{\fbox{4}}\)

領域、直線の式、座標の設定と座標を求める関数の総合問題です。

条件
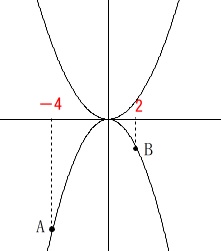
　\(\displaystyle y=\frac{1}{3}x^2　･･･①\)
　\(\displaystyle y=-\frac{1}{2}x^2　･･･②\)
　\(\,\mathrm{A,B}\,\)は②上の点で\(\,x\,\)座標がそれぞれ\(\,-4\,,\,2\,\)

※
座標軸の単位の長さは\(\,\mathrm{1\,cm}\,\)ですが省略して計算は進めます。

(1)
①において\(\,y\,\)の変域を求めます。

\(\,x\,\)の変域（定義域）が
　\(-3\,≦\,x\,≦\,1\)
のときは軸をはさむことに気をつけて
　最小値\(\,x=0\,\)のとき\(\,y=0\,\)
　最大値\(\,x=-3\,\)のとき\(\,y=3\,\)
だから\(\,y\,\)の変域（値域）は
　\(\hspace{4pt}\underline{　0\,≦\,y\,≦\,3　}\)
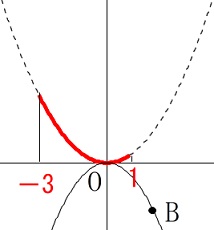\(\,x=1\,\)で最小ではありません。

(2)
直線\(\,\mathrm{AB}\,\)の式を求めます。

\(\,2\,\)点
　\(\mathrm{A}\,(\,-4\,,\,-8\,)\)
　\(\mathrm{B}\,(\,2\,,\,-2\,)\)
を通る直線なので
　\(\hspace{4pt}\underline{　y=x-4　}\)

ちょっと長くなっているので途中を省略しました。
\(\,2\,\)点を通る直線は求まられるようにはなっておきましょう。

(3)
座標を設定し、条件に合うように座標を決定します。

関数は①\(\displaystyle \,y=\frac{1}{3}x^2\,\)のまま条件が加わります。

条件
　点\(\,\mathrm{P}\,\)は\(\,x\,\)座標が正である①上の点
　点\(\,\mathrm{P}\,\)を通り\(\,x\,\)軸と平行な直線と\(\,y\,\)軸との交点を\(\,\mathrm{C}\,\)とする。

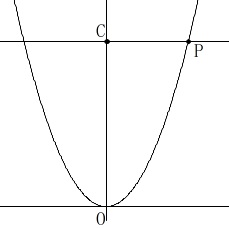
ア
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)としたときの\(\,y\,\)座標です。

点\(\,\mathrm{P}\,\)は関数①\(\displaystyle \displaystyle \,y=\frac{1}{3}\,x^2\,\)上の点なので、
\(\,x\,\)座標が\(\,t\,\)のとき\(\,y\,\)座標は
　\(\hspace{4pt}\displaystyle \underline{　\frac{1}{3}\,t^2　}\)

イ
　\(\,\mathrm{OC+CP=\color{red}{18}}\,\)
のときの点\(\,\mathrm{P}\,\)の座標を求めます。

点\(\,\mathrm{P}\,\)の座標は
　\(\displaystyle \,\mathrm{P}\,\left(\,t\,,\,\frac{1}{3}\,t^2\,\right)\,\)

\(\,\mathrm{OC}\,\)は\(\,\mathrm{C}\,\)の\(\,y\,\)座標\(\displaystyle \,\color{blue}{\frac{1}{3}\,t^2}\,\)
\(\,\mathrm{CP}\,\)は\(\,\mathrm{P}\,\)と\(\,\mathrm{C}\,\)の\(\,x\,\)座標の差\(\,\color{magenta}{t}\,\)
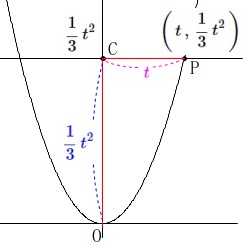これから
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{1}{3}\,t^2}+\color{magenta}{t}&=&\color{red}{18}\\
t^2+3t&=&54\\
t^2+3t-54&=&0\\
(t+9)(t-6)&=&0\\
t&=&-9\,,\,6
\end{eqnarray}\)

\(\,t\,＞\,0\,\)であることを考えて
　\(\,\mathrm{P}\,\underline{　(\,6\,,\,12\,)　}\,\)

第５問変化の読み取り問題

\(\color{black}{\fbox{5}}\)
問題の意味を読み取る\(\,1\,\)次関数の問題です。

単位\(\,\mathrm{cm}\,\)を省略してまとめると、
　横\(\,45\,\)縦\(\,20\,\)高さ\(\,30\,\)の直方体の水槽があって、
　仕切り①②で\(\,15\,\)間隔で\(\,\mathrm{A,B,C}\,\)に\(\,3\,\)分割している。
　仕切り①の高さは\(\,a\,\)
　仕切り②の高さは\(\,21\,\)
　\(\,\mathrm{A}\,\)側から水を一定の割合で入れていく。

図\(\,1\,\)図\(\,2\,\)に水槽を真横から見た図を加えておきます。
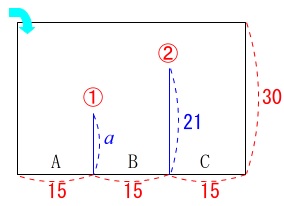左の\(\,\mathrm{A}\,\)側から水がたまっていきます。

(1)
仕切り①の高さ\(\,a\,\)を求めます。

底面\(\,\mathrm{A}\,\)の部分がいっぱいになると、
底面\(\,\mathrm{B}\,\)の部分にたまりはじめます。
底面\(\,\mathrm{B}\,\)だけにたまっている間は\(\,\mathrm{A}\,\)の水面の高さは変わりません。

図\(\,4\,\)のグラフから
　\(\,a=\underline{　12　}\,\)

(2)
底面\(\,\mathrm{A}\,\)の部分では\(\,4\,\)分で高さが\(\,12\,\)上昇するので、
\(\,1\,\)分間に\(\,3\,\)上昇します。

底面\(\,\mathrm{B}\,\)の部分でも仕切り①を超えるまでは、
\(\,1\,\)分間に\(\,3\,\)上昇しますが、
それを超えると底面\(\,\mathrm{A,B}\,\)分の底面積が\(\,2\,\)倍になるので
\(\,1\,\)分間に\(\displaystyle \,\frac{3}{2}=1.5\,\)の上昇になります。

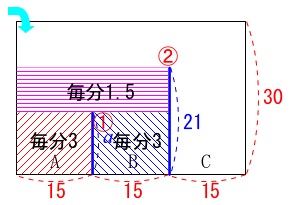
図\(\,3\,\)の数値をうめていきます。
　\(\begin{array}{|c|c|c|} \hline
\,時間\, & \,\mathrm{A}\,の高さ\,　&\, \mathrm{B}\,の高さ\,　\\ \hline
0 & 0 & 0 \\ \hline
1 & 3 & 0 \\ \hline
2 & 6 & 0 \\ \hline
3 & 9 & 0 \\ \hline
4 & 12 & 0 \\ \hline
5 & 12 & 3 \\ \hline
6 & 12 & 6 \\ \hline
7 & 12 & 9 \\ \hline
8 & 12 & 12 \\ \hline
9 & 13.5 & 13.5 \\ \hline
10 & 15 & 15 \\ \hline
11 & 16.5 & 16.5 \\ \hline
12 & 18 & 18 \\ \hline
\cdots & \cdots & \cdots \\ \hline
\end{array}\)
　
答え　あ　\(\,\underline{　3　}\,\)　い　\(\,\underline{　3　}\,\)　う　\(\,\underline{　12　}\,\)

(3)
底面\(\,\mathrm{B}\,\)の水面の高さを\(\,y\,\)としたときのグラフをかきます。
ただし、\(\,4\,≦\,x\,≦\,14\,\)です。

　\(\,4\,\)分までは\(\,\mathrm{A}\,\)だけなので\(\,y=0\,\)
　その後高さ\(\,12\,\)までは毎分\(\,3\,\)で\(\,\mathrm{B}\,\)は上昇する。
　高さ\(\,12\,\)を超えると毎分\(\,1.5\,\)で上昇する。
　②の仕切り高さ\(\,21\,\)まで上昇すると底面\(\,\mathrm{C}\,\)の部分だけにたまり出す。

底面\(\,\mathrm{C}\,\)でも最初は毎分\(\,3\,\)で仕切り②の\(\,21\,\)まで、
\(\,7\,\)分間たまりますが、
底面\(\,\mathrm{C}\,\)の部分にたまりはじめるのは\(\,14\,\)分以降なので必要ありません。
(2)で書いた表の点をつないで、
\(\,8\,\)分後に変化することが分かればグラフはかけます。

もちろん、部分部分を関数にしても良いですよ。
\(\,0\,≦\,x\,≦\,4\,\)のとき
　\(\hspace{4pt}y=0\)
\(\,4\,≦\,x\,≦\,8\,\)のとき
　\(\hspace{4pt}y=3x-12\)
\(\,8\,≦\,x\,≦\,14\,\)のとき
　\(\hspace{4pt}\displaystyle y=\frac{3}{2}x\)

グラフをかくだけなら必要ありません。

(4)
\(\,20\,\)分後の底面\(\,\mathrm{C}\,\)の部分の水面の高さを求めます。

底面\(\,\mathrm{C}\,\)の部分には\(\,14\,\)分後から毎分\(\,3\,\)でたまりはじめます。

仕切り②の\(\,21\,\)まで\(\,7\,\)分間は\(\,\mathrm{C}\,\)だけにはたまるので、
\(\,20\,\)分後はまだ毎分\(\,3\,\)の割合で上昇しています。

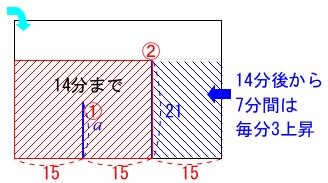
\(\,14\,\)分から\(\,20\,\)分までの\(\,6\,\)分間なので
　\(\hspace{10pt}3\times 6\\
=\underline{　18　\mathrm{cm}}\)

以上です。

詳しく説明したわけではありません。
実際にはもっとですが、
中学生が問題を解く際に手を動かしている部分を書いていくとこうなります。

しかし、『覚え太郎』レベルの数学の言葉を覚えている人は、
おそらく試験時間はかなり余ったのではないでしょうか。

⇒　青森県公立高校入試2019年(平成31年)度の数学問題と解説

\(\,2019\,\)年度は平均点が\(\,10\,\)点以上低かったようですが、
教科書の基本というより、数学の基本通りやれば変わりないでしょう。
　
⇒　青森県の公立高校入試数学の過去問と解説

基本重視だということは過去数年分の問題を見ればわかります。
\(\,2021\,\)年度は特に基礎、基本重視の群馬県公立入試です。