2019年度三重県公立高校入試後期の数学の問題と解説

2019年（平成31年）度三重県で行われた公立高校入試数学の問題と解説です。
例年通りの大きく５問で構成され幅広い範囲から偏りなく出題されています。
第５問は問題の流れをしっかり追わなければ差がつきそうな計算力、応用ともに問われます。

2019年(平成31年)三重県公立高校入試後期選抜の数学の問題と解説

三重県の公立入試数学は\(\,50\,\)点満点です。
平成\(\,31\,\)年度後期の平均点は\(\,26.5\,\)点です。

2019年(平成31年)三重県公立高校入試後期選抜の数学の問題

問題　⇒　2019年度後期選抜の数学の問題

2019年(平成31年)三重県公立高校入試後期選抜の数学の解説

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであります。
試験時間は\(\,45\,\)分です。

応用となる\(\color{black}{\fbox{5}}\)の他は基本問題なので解説を簡単に済ませます。

第１問基本的な計算小問集合

\(\color{black}{\fbox{1}}\)

基本的な計算問題が\(\,7\,\)問あります。

(1)
　\(\hspace{10pt}(-20)\div 4\\
=\underline{　-5　}\)

符号にだけは気をつけましょう。

(2)
　\(\hspace{10pt}\displaystyle \frac{x}{2}-\frac{x}{3}\\
\displaystyle =\frac{3x-2x}{6}\\
\displaystyle =\underline{　\frac{x}{6}　}または　\underline{　\frac{1}{6}x　}\)

分数の加減（足し算引き算）の計算は通分して分母を1つにするのが早いです。

(3)
　\(\hspace{10pt}3(a+2b)-(2a-b)\\
=3a+6b-2a\color{red}{+b}\\
=\underline{　a+7b　}\)

\(\,2\,\)行目を省いて暗算すると計算ミスが増えます。

(4)
　\(\hspace{10pt}(\sqrt{7}-2\sqrt{5})(\sqrt{7}+2\sqrt{5})\\
=(\sqrt{7})^2-(2\sqrt{5})^2\\
=7-20\\
=\underline{　-13　}\)

普通に展開しても良いですが公式
　\(\hspace{4pt}\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用しました。

(5)
　\(\hspace{10pt}x^2-x-30\\
=\underline{　(x+5)(x-6)　}\)

普通の因数分解です。
定数項\(\,-30\,\)に着目して
　\(\,1\times 30\,,\,2\times 15\,,\,3\times 10\,,\,5\times 6\,\)
の中からどちらかにマイナスをつけて、
足して\(\,1\,\)次の項の係数\(\,-1\,\)になる組み合わせを探します。
　\(\hspace{4pt}(+5)+(-6)=-1\,\)

(6)
\(\,2\,\)次方程式を解きます。
　\(\hspace{4pt}2x^2-3x-1=0\)
因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{3\pm \sqrt{3^2-4\cdot 2\cdot (-1)}}{2\times 2}\\
&=&\frac{3\pm \sqrt{9+8}}{4}\\
&=&\underline{　\frac{3\pm \sqrt{17}}{4}　}
\end{eqnarray}\)

(7)
条件通りに比例式を立てれば良いだけです。
取り出した白玉の数を\(\,x\,\)とします。

白玉は\(\,\mathrm{B}\,\)だけに入っている玉で、
\(\,\mathrm{B}\,\)から取り出した玉の数が\(\,x\,\)個ということです。

　\(\begin{array}{|c|c|c|} \hline
& \mathrm{A}\,の箱 & \mathrm{B}\,の箱 \\ \hline
最初 & 45 & 27 \\ \hline
取り出す玉 & 2x & x \\ \hline
残りの玉 & 45-2x & 27-x \\ \hline
\end{array}\)
（表にしなくても良いですよ。）

残った赤玉と白玉の比が\(\,7:5\,\)なので
（\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)に残った個数の比です。）

　\(\begin{eqnarray}\displaystyle
(45-2x):(27-x)&=&7:5\\
7(27-x)&=&5(45-2x)\\
189-7x&=&225-10x\\
-7x+10x&=&225-189\\
3x&=&36\\
x&=&\underline{　12　個}
\end{eqnarray}\)

第２問データの活用と連立方程式

\(\color{black}{\fbox{2}}\)はデータの活用の代表値と連立方程式の問題です。

(1)
\(\,6\,\)人の借りた本の冊数についてデータがあります。

基準を\(\,6\,\)冊としたときのそれぞれのデータが
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
& \,\mathrm{A}\, & \,\mathrm{B}\, & \,\mathrm{C}\, & \,\mathrm{D}\, & \,\mathrm{E}\, & \,\mathrm{F}\, \\ \hline
基準との差 & +10 & 0 & +2 & -3 & +4 & -1 \\ \hline
借りた冊数 & 16 & 6 & 8 & 3 & 10 & 5 \\ \hline
\end{array}\)

①
平均値を出すだけなら実際に借りた冊数は必要ありませんが、
ここでは書き出しました。
これくらいのデータの大きさ（数）なら、
そのままのデータをあつかった方が分かり易いからです。

基準値からの差を利用した平均値
　\(\hspace{10pt}\displaystyle \frac{10+0+2-3+4-1}{6}\\
\displaystyle =\frac{+12}{6}\\
=+2\)

これは基準\(\,+6\,\)からのズレなので
　\(\hspace{10pt}　6+2=\underline{　8　冊}\)

実際に借りた冊数で計算すると、
　\(\hspace{10pt}\displaystyle \frac{16+6+8+3+10+5}{6}\\
\displaystyle =\frac{48}{6}\\
=\underline{　8　冊}\)

実際に借りた本の冊数を書き出す手間を惜しまなければ、
普通に平均値を求めるのと同じです。

②
今度は\(\,6\,\)人のデータの中央値です。

基準との差でも、実際に借りた冊数でもどちらでも良いですが、
どちらにしてもデータの小さい順に並べるのが基本です。

基準からのズレで見ると、
　\(-3\,,\,-1\,,\,\color{red}{0}\,,\,\color{red}{+2}\,,\,+4\,,\,+10\)

データの数が偶数なので真ん中2つの平均が中央値になるので、
　\(\hspace{10pt}\displaystyle \frac{\color{red}{0}+\color{red}{2}}{2}\\
=+1\)

これは基準からのズレなので
　\(\hspace{4pt}6+1=\underline{　7　冊}\)

実際の借りた冊数で見ると
　\(3\,,\,5\,,\,\color{blue}{6}\,,\,\color{blue}{8}\,,\,10\,,\,16\)

中央値は
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{6}+\color{blue}{8}}{2}\\
=\underline{　7　冊}\)

データを扱うときは、
　「小さい順に並べ直す。」
というのはデータの数にもよりますがやっておいた方が良いですよ。

(2)
値段（金額）についての連立方程式です。

条件を整理しておきます。

　ノート\(\,1\,\)冊とボールペン\(\,1本\,\)を定価で買うと\(\,145\,\)円
　ノートが\(\,10\,\)％引き、ボールペンが\(\,20\,\)％引きのとき、
　ノート\(\,2\,\)冊とボールペン\(\,3\,\)本を買うと合計は\(\,294\,\)円

この関係を文字式で連立します。

ノート\(\,1\,\)冊の定価を\(\,x\,\)円、ボールペン\(\,1\,\)本の定価を\(\,y\,\)円とします。

\(\,10\,\)％引き、\(\,20\,\)％引き後の価格をどう表すかは好きにしていいです。

小数で表すと\(\,0.9x\,,\,0.8y\,\)です。
分数で表すと\(\,\displaystyle \frac{90}{100}x\,,\,\frac{80}{100}y\,\)です。

条件を連立すると
　\(\begin{cases}
\hspace{4pt} \underline{　x+y　}=145\\
\hspace{4pt} \underline{　0.9x\times 2+0.8y\times 3　}=294
\end{cases}\)
または
　\(\begin{cases}\displaystyle
\hspace{4pt} \underline{　x+y　}=145\\
\hspace{4pt} \displaystyle \underline{　\frac{90}{100}x\times 2+\frac{80}{100}y\times 3　}=294
\end{cases}\)

いずれも小数分数を無くす処理をすると、
　\(\begin{cases}\displaystyle
\hspace{4pt} x+y=145\\
\hspace{4pt} 3x+4y=490
\end{cases}\)

連立方程式を解くときは一文字消去が基本になります。
代入法でも加減法でも何でも良いです。

　\(\hspace{12pt}3x+3y=435\\
\underline{-)\,3x+4y=490}\\
\hspace{30pt}-y=-55\\
\hspace{42pt}y=\underline{　55　}\)

これを連立した方程式のどれでもいいから代入すると
　\(\begin{eqnarray}\displaystyle
x+(55)&=&145\\
x&=&\underline{　90　}
\end{eqnarray}\)

よって、
　ノート\(\,1\,\)冊の定価は\(\,\underline{　90　}\,\)円
　ボールペン\(\,1\,\)本の定価は\(\,\underline{　55　}\,\)円

\(\color{black}{\fbox{　②　}}\)に入れる方程式は右辺が\(\,294\,\)になる形であれば、
掛け算した後のものでも問題ないでしょう。

(3)
硬貨\(\,4\,\)枚の確率です。
表か裏かの場合だけなので全部で\(\,16\,\)通りです。

書き出すでしょう。
樹形図の方が早いですが、表にしておきます。

表を\(\,○\,\)、裏を\(\,×と\,\)します。
②も含めて合計金額も書き出しておきますが、
\(\,500\,\)円硬貨が表の場合だけ見ていればおおよそ見えてきます。

\(\,500\,\)円が表の場合
　\(\begin{array}{|c|c|c|c|c|} \hline
500 & 100 & 50 & 10 & 合計金額 \\ \hline
○ & ○ & ○ & ○ & 660 \\ \hline
○ & ○ & ○ & × & 650 \\ \hline
○ & ○ & × & ○ & 610 \\ \hline
○ & ○ & × & × & 600 \\ \hline
○ & × & ○ & ○ & 560 \\ \hline
○ & × & ○ & × & 550 \\ \hline
○ & × & × & ○ & 510 \\ \hline
○ & × & × & × & 500 \\ \hline
\end{array}\)

\(\,500\,\)円が裏の場合
　\(\begin{array}{|c|c|c|c|c|} \hline
500 & 100 & 50 & 10 & 合計金額 \\ \hline
× & ○ & ○ & ○ & 160 \\ \hline
× & ○ & ○ & × & 150 \\ \hline
× & ○ & × & ○ & 110 \\ \hline
× & ○ & × & × & 100 \\ \hline
× & × & ○ & ○ & 60 \\ \hline
× & × & ○ & × & 50 \\ \hline
× & × & × & ○ & 10 \\ \hline
× & × & × & × & 0 \\ \hline
\end{array}\)

①
少なくとも\(\,1\,\)枚は表になる確率です。
　\(\hspace{10pt}\displaystyle \underline{　\frac{15}{16}　}\)

「少なくとも\(\,\mathrm{A}\,\)」という場合は、
「すべて\(\,\mathrm{A}\,\)ではない。」確率を\(\,1\,\)から引くというのが早いです。

ここでは「すべて裏」の確率を\(\,1\,\)から引くということです。
　\(\hspace{10pt}\displaystyle 1-\frac{1}{16}\\
=\displaystyle \underline{　\frac{15}{16}　}\)

②
これも答えは出ています。
　\(\hspace{10pt}\displaystyle \underline{　\frac{7}{16}　}\)

確率は考えて計算しなくてはいけないと思い込んでいる人がいますが、
どのような場合があるか、「場合」を書き出すことから始まります。

第３問関数総合問題

放物線や\(\,1\,\)次関数や定直線が与えられたグラフがあります。

条件
　\(\,y=ax^2　･･･㋐\,\)
　\(\,y=-x+6　･･･㋑\,\)
　\(\,\mathrm{A,B}\,\)は\(\,㋐㋑\,\)の交点
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,3\,\)
　\(\,\mathrm{B}\,\)の座標は\(\,(\,-6\,,\,p\,)\,\)
　\(\,\ell\,\)は\(\,y\,\)軸に平行で\(\,x\,＜\,0\,\)
　\(\,\mathrm{E,F,G}\,\)は\(\,\ell\,\)との交点
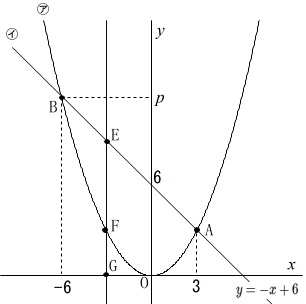読み取れることは書き込んでおいた方が良いですが、
問題に沿って進めます。

(1)
\(\,\mathrm{A,B}\,\)は\(\,㋐㋑\,\)の交点なので、
どちらに代入しても成り立ちます。

\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,3\,\)なので、
\(\,㋑\,\)から\(\,\mathrm{A}\,\)の\(\,y\,\)座標は
　\(\begin{eqnarray}\displaystyle
y&=&-(3)+6\\
&=&3
\end{eqnarray}\)

これから
　\(\hspace{4pt}\mathrm{A}\,(\,3\,,\,3\,)\)

\(\,\mathrm{A}\,\)は関数\(\,y=ax^2\,\)上の点でもあるので
　\(\begin{eqnarray}\displaystyle
3&=&a\times (3)^2\\
a&=&\underline{　\frac{1}{3}　}
\end{eqnarray}\)

このとき関数\(\,㋐\,\)は
　\(\hspace{10pt}\displaystyle y=\frac{1}{3}\,x^2\)

点\(\,\mathrm{B}\,(\,-6\,,\,p\,)\,\)は\(\,㋐\,\)上の点なので
　\(\begin{eqnarray}\displaystyle
p&=&\frac{1}{3}\times (-6)^2\\
&=&\underline{　12　}
\end{eqnarray}\)

(2)
\(\,x\,\)の変域が\(\,-2\,≦\,x\,≦\,4\,\)のときの
　\(\displaystyle \,y=\frac{1}{3}\,x^2\,\)の\(\,y\,\)の変域は

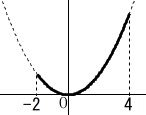
\(\,x=0\,\)で最小値\(\,y=0\,\)
\(\,x=4\,\)のとき最大値
　\(\hspace{4pt}\displaystyle y=\frac{1}{3}\times (4)^2=\frac{16}{3}\)
となります。

　\(\hspace{10pt}\displaystyle \underline{　0\,≦\,y\,≦\,\frac{16}{3}　}\)　

\(\,x=-2\,\)のときは最大最小には関係ありません。

(3)
\(\,\mathrm{EF=2FG}\,\)となるときの点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を求めます。

あれこれ考えるより文字設定した方が早いでしょう。

\(\,\mathrm{E,F,G}\,\)の\(\,x\,\)座標は同じなので、
点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を\(\,\color{red}{t}\,(\,t\,＜\,0\,)\)とすると
　\(\,\mathrm{G}\,(\,t\,,\,0\,)\,\)
　\(\displaystyle \,\mathrm{F}\,\left(\,t\,,\,\frac{1}{3}\,t^2\,\right)\,\)
　\(\,\mathrm{E}\,(\,t\,,\,-t+6\,)\,\)
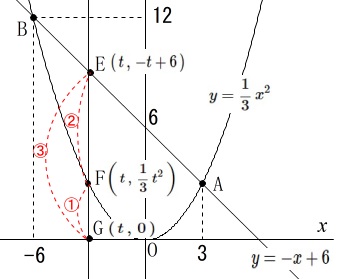見にくいですが\(\,\mathrm{E,F,G}\,\)の\(\,y\,\)座標に注目してください。

\(\,\mathrm{EG:FG=3:1}\,\)になるので
　\(\begin{eqnarray}\displaystyle
(-t+6):\frac{1}{3}\,t^2&=&3:1\\
t^2&=&-t+6\\
t^2+t-6&=&0\\
(t+3)(t-2)&=&0\\
t&=&-3\,,\,2
\end{eqnarray}\)

\(\,t\,＜\,0\,\)なので
　\(\hspace{10pt}\color{red}{t}=\underline{　-3　}\,\)

(4)
\(\,x\,\)軸上の正の範囲に\(\,\mathrm{C}\,\)をとり
　\(\,\mathrm{△ABC\,=\,△OAB}\,\)
となるときの\(\,\mathrm{C}\,\)の座標を求めます。
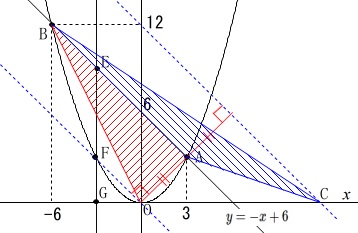良くある問題なので説明はそれほど必要無いとは思いますが、
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△OAB}\,\)は底辺を同じ\(\,\mathrm{AB}\,\)と見ると、
高さが等しければ面積も等しくなります。

\(\,\mathrm{△OAB}\,\)の高さは\(\,\mathrm{OA}\,\)ですが、
原点\(\,\mathrm{O}\,\)を通り\(\,\mathrm{AB}\,\)に平行な直線上の点であれば高さは等しくなります。

点\(\,\mathrm{C}\,\)は底辺\(\,\mathrm{AB}\,\)とすると\(\,\mathrm{O}\,\)とは反対側にあるので、
\(\,\mathrm{AB}\,\)に平行で同じ高さとなる直線上にあれば良いので、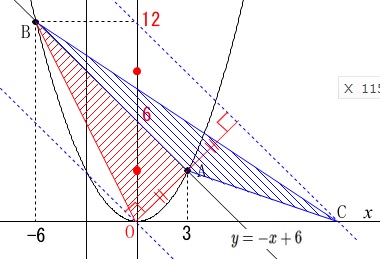
切片が\(\,\mathrm{AB}\,\)の\(\,+6\,\)の\(\,2\,\)倍の\(\,12\,\)の直線
　\(\hspace{10pt}y=-x+12\)
上にあれば良いことになります。

\(\,x\,\)軸上の点\(\,\mathrm{C}\,\)の座標は\(\,y=0\,\)なので
　\(\begin{eqnarray}\displaystyle
0&=&-x+12\\
x&=&12
\end{eqnarray}\)

よって、
　\(\hspace{10pt}\mathrm{C}\,\underline{　(\,12\,,\,0\,)　}\)

点\(\,\mathrm{C}\,\)の座標を\(\,(\,k\,,\,0\,)\,\)とおいて、
面積計算をしても出てきます。

ただし、会員以外は見なくて良いです。
　\(\begin{eqnarray}\displaystyle
|-18-36|&=&|(k+6)3-12(k-3)|\\
54&=&|-9k+54|\\
k&=&0\,,\,\underline{　12　}
\end{eqnarray}\)
（\(\,k=0\,\)は原点\(\,\mathrm{O}\,\)のときです。）

絶対値を外すときは注意しましょう。

第４問作図と円すいの性質

ひし形の作図と円すいの典型問題です。

(1)
四角形\(\,\mathrm{ABCD}\,\)にひし形\(\,\mathrm{PBQR}\,\)を作図します。

条件
　点\(\,\mathrm{P}\,\)は辺\(\,\mathrm{AB}\,\)上の点
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{BC}\,\)上の点
　点\(\,\mathrm{R}\,\)は\(\,\mathrm{DC}\,\)上の点
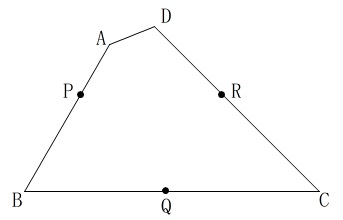ひし形の定義、定理から考えます。

ひし形は平行四辺形であり、\(\,4\,\)辺が等しく対角線がそれぞれの中点で直交します。
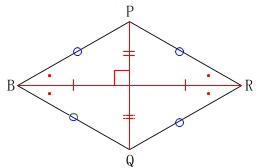\(\,4\,\)辺が等しいことから、
\(\,\mathrm{R}\,\)を定めるのは難しいです。
\(\,\mathrm{R}\,\)が\(\,\mathrm{∠PBQ}\,\)の二等分線上にあることからはじめるのが正解でしょう。

\(\,\mathrm{∠ABC}\,\)の二等分線を引いて対策線を決めます。
辺\(\,\mathrm{DC}\,\)との交点が\(\,\mathrm{R}\,\)です。

この後線分\(\,\mathrm{AR}\,\)の垂直二等分線を引いて、
\(\,\mathrm{AB,BC}\,\)との交点を\(\,\mathrm{P,Q}\,\)とし、
線分\(\,\mathrm{PR,QR}\,\)を描けばひし形ができあがります。
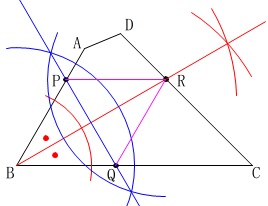ひし形の定理の確認問題でした。

(2)
円すい\(\,\mathrm{P}\,\)があります。

円すい\(\,\mathrm{P}\,\)の条件
　底面の直径\(\,\mathrm{AB}\,\)は\(\,6\,\)
　母線の長さは\(\,6\,\)
（長さは\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）

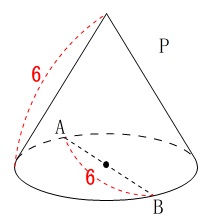
①
円すい\(\,\mathrm{P}\,\)の体積を求めます。

すい体の体積\(\,V\,\)は底面の形に関係なく、
　\(\displaystyle V=\frac{1}{3}\times (\color{red}{底面積})\times (\color{blue}{高さ})\)
です。

円すい\(\,\mathrm{P}\,\)は底面の半径が\(\,3\,\)なので底面積\(\,\color{red}{S}\,\)は
　\(\begin{eqnarray}\displaystyle
\color{red}{S}&=&\pi\times (3)^2\\
&=&9\,\pi
\end{eqnarray}\)

高さは中心と頂点を通る面で円すいを切ると正三角形になるので
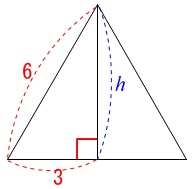高さ\(\,\color{blue}{h}\,\)は
　\(\hspace{10pt}\color{blue}{h}=3\sqrt{3}\)　

よって、円すい\(\,\mathrm{P}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \color{red}{S}\times \color{blue}{h}\\
&=&\frac{1}{3}\times 9\,\pi\times 3\sqrt{3}\\
&=&\underline{　9\sqrt{3}\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)

②
円すい\(\,\mathrm{P}\,\)の側面積を求めます。

母線と底面の半径が分かっているので側面積を\(\,S_2\,\)とすると
　\(\begin{eqnarray}\displaystyle
S_2&=&6\times 3\times \pi\\
&=&\underline{　18\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)
と、公式で求めることもできますが、
これは教科書には無い公式だと思うので普通に説明しておきます。

表面積や側面積を求めるときは先ず展開図です。
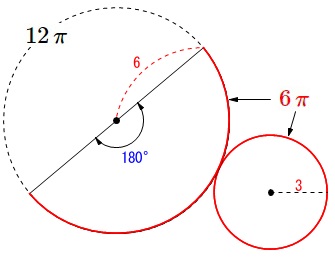半径\(\,6\,\)の円の周は\(\,12\,\pi\,\)で、
底面の周と側面の扇形の弧の長さが\(\,\color{red}{6\,\pi}\,\)で等しくなるので、
扇形の中心角が\(\,180°\,\)で半円です。

よって、側面積は
　\(\hspace{10pt}\displaystyle \pi\times (6)^2\times \frac{180}{360}\\
=\underline{　18\,\pi　\mathrm{cm^2}}\)

扇形の弧の長さが\(\,\ell\,\)、半径が\(\,r\,\)のとき
扇形の面積\(\,S\,\)は
　\(\hspace{10pt}\displaystyle S=\frac{1}{2}\,\ell\,r\)
でもあるので、
弧の長さが\(\,6\,\pi\,\)と分かったときの扇形の面積は
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\,\pi\times 6\\
=\underline{　18\,\pi　\mathrm{cm^2}}\)
でも良いですね。

③
円すいの側面に点Aから点Bまでゆるまないようにひもをかけます。
そのときかけたひもが最も短くなるひもの長さを求めます。

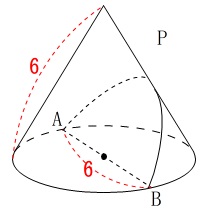
「最も短い」というのは距離と同じことです。
つまり、平面で見るときには直線でつながるときに最短となります。

平面で見るのは展開図です。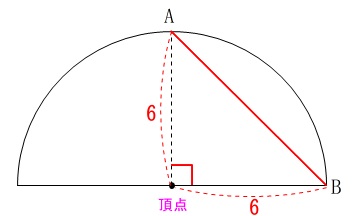\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)は円の反対側にあるので、
展開図では弧の半分の位置になります。

中心角が\(\,180°\,\)だったので、
\(\,\mathrm{AB}\,\)をつなぐひもの長さが最も短くなるのは、
　\(\hspace{10pt}\underline{　6\sqrt{2}　\mathrm{cm}}\)

第５問相似と合同の証明および線分の長さと面積比

\(\color{black}{\fbox{5}}\)

相似の証明、合同の証明、線分の長さ、面積比と平面図形ですが総合問題です。

この問題のポイントは流れに乗るということです。
(3)の①②がなければ③は難問ですね。

条件です。
　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{AF}\,\)∥\(\,\mathrm{EB}\,\)

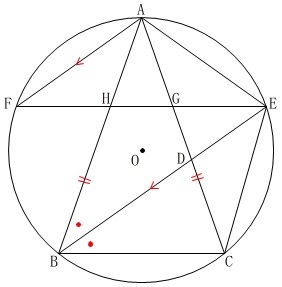
(1)
相似の証明です。
穴埋めなので図を見ながらうめていきましょう。
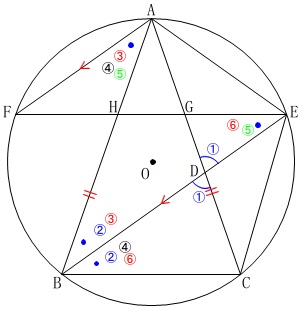条件の番号を追っていけば分かるので確認してください。
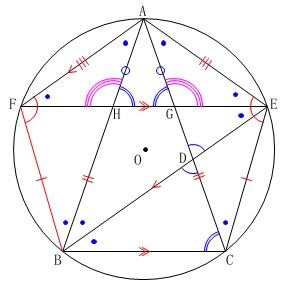
　\(\,\mathrm{△DBC}\,\)と\(\,\mathrm{△DEG}\,\)において
　\(\,\mathrm{∠BDC}=\,\)\(\color{black}{\fbox{　∠EDG　}}\)　･･･①
　\(\,\mathrm{∠DBC}=\,\)\(\color{black}{\fbox{　\(\,\mathrm{\color{red}{∠ABD}}\,\)　}}\)　･･･②
　\(\,\color{black}{\fbox{　\(\,\mathrm{\color{red}{∠ABD}}\,\)　}}\)\(\,\mathrm{=∠BAF　}\,\)･･･③
　\(\,\mathrm{∠DBC=∠BAF}\,\)　･･･④
　\(\,\mathrm{∠BAF=∠DEG}\,\)　･･･⑤
　\(\,\mathrm{∠DBC=∠DEG}\,\)　･･･⑥
①⑥より、\(\color{black}{\fbox{　2組の角　}}\)がそれぞれ等しいので、
　\(\,\mathrm{△DBC}\,\)　∽　\(\,\mathrm{△DEG}\,\)

②③に入る\(\,\mathrm{∠ABD}\,\)は同じ角を表していれば記号の順番、種類は違っていても構いません。

相似の証明なので、
相似な三角形の角どうしなどを記号で表すときは記号の順番に気をつけましょう。
角度が等しい、辺が等しいなど、等しいことだけいえば良い場合は気にしなくて良いです。

この問は穴埋めなので難しくはないでしょうから先に進みます。

(2)
今度は合同の証明です。
\(\,\mathrm{△AEG}\,\)≡\(\,\mathrm{△AFH}\,\)を証明します。

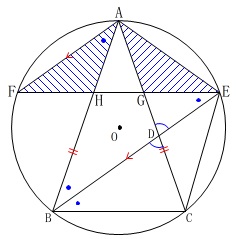
もう一度条件を確認しておきましょう。
　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{AF}\,\)∥\(\,\mathrm{EB}\,\)
さらに(1)において
　\(\,\mathrm{△DBC}\,\)　∽　\(\,\mathrm{△DEG}\,\)
が追加されています。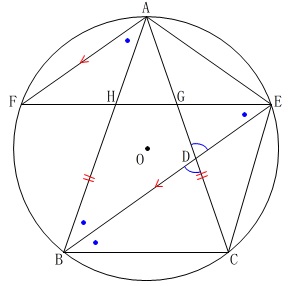図の中で証明しておきましょう。

先ずは円周角で等しいところ、
および平行線で等しくなる角、
さらに錯角が等しいことから新たな平行線が出てくるので書き込んでおきます。
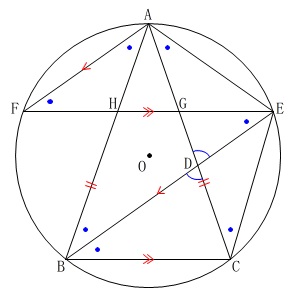円周角は同じ弧の円周角が等しいことから分かります。

　\(\,\mathrm{∠CBE=∠FEB}\,\)
で錯角が等しいので
　\(\,\mathrm{FE}\,\)　∥　\(\,\mathrm{BC}\,\)
でもあります。

これだけでも十分証明はできますが、
\(\,\mathrm{BF}\,\)を結ぶと仮定から\(\,\mathrm{AB=AC}\,\)だから、
弦の長さが等しいとき円周角も等しく
　\(\,\mathrm{∠AFB=∠AEC}\,\)
となるので三角形の内角の和から
　\(\,\mathrm{∠ABF=∠ACE}\,\)
であることもいえるので
　\(\,\mathrm{△ABF}\,\)　≡　\(\,\mathrm{△ACE}\,\)
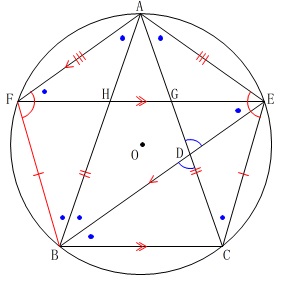1つの弧\(\,\mathrm{AF}\,\)の円周角が等しいので
　\(\,\mathrm{∠ABF=∠AEF}\,\)
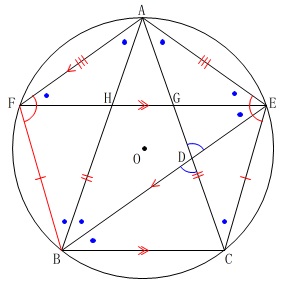これで簡単に合同が言えます。

\(\,\mathrm{△ABC}\,\)が二等辺三角形で底角が等しいことと、
弧\(\,\mathrm{AB}\,\)の円周角から
　\(\,\mathrm{∠ACB=∠AEB\,(=2\times \color{blue}{●}\,)}\,\)
なので
　\(\,\mathrm{∠AEB=∠BEF=∠CAE\,(=\color{blue}{●}\,)}\,\)
などもいえます。

また、
　\(\,\mathrm{FE}\,\)　∥　\(\,\mathrm{BC}\,\)
なので
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△AHG}\,\)
だから\(\,\mathrm{△AHG}\,\)も二等辺三角形であることがいえるので
　\(\,\mathrm{AG=AH}\,\)
　\(\,\mathrm{∠AGE=∠AHF}\,\)
であることから合同をいってもいいです。
いずれにしても等しいことを見つけた順に時間の許す限り、
日本語でつなぎ合わせれば、
　「\(\,1\,\)組の辺とその両端角がそれぞれ等しい。」
または
　「\(\,2\,\)組の辺とその間の角がそれぞれ等しい。」
という合同条件にたどり着きます。

早いのは
　「\(\,1\,\)組の辺とその両端角がそれぞれ等しい。」
です。

どの合同条件にたどり着くか図の中で確認しておいて、
その条件を一つひとつ書き出して行くことで解決します。

とにかく等しい角度が多いし、
合同な三角形も多いから条件の拾い出しに迷うくらいですが、
すべてを書き出していたら時間もかかりますから気がついた順に拾い出していくしかないですね。
決して難しい証明ではありません。

(3)
長さと面積比を求める問題です。
この問題でのポイントは流れに乗れるかどうかです。
　
長さの条件が加わります。

　\(\,\mathrm{AB=3}\,\)
　\(\,\mathrm{BC=2}\,\)
二等辺三角形なので
　\(\,\mathrm{AC=3}\,\)

ただし、忘れていけないのは(1)(2)で証明したことです。

　\(\,\mathrm{△DBC}\,\)　∽　\(\,\mathrm{△DEG}\,\)
　\(\,\mathrm{△AEG}\,\)　≡　\(\,\mathrm{△AFH}\,\)

①
線分\(\,\mathrm{ＣＤ}\,\)の長さを求めます。
これは(1)(2)の誘導無しでも求まります。

角の二等分線定理を使えば
　\(\,\mathrm{AD:DC=3:2}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{ＣＤ}&=&3\times \frac{2}{3+2}\\
&=&\underline{　\frac{6}{5}　\mathrm{cm}}
\end{eqnarray}\)
と即座に出ますが、高校入試の解説としては不適切でしょう。
（会員は当たり前に使って良いですよ。）

方法は2つありますが、ここでは平行線をもう一つ足しておきます。

\(\,\mathrm{D}\,\)を通り\(\,\mathrm{BC}\,\)に平行な線を引き、
\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{K}\,\)とします。
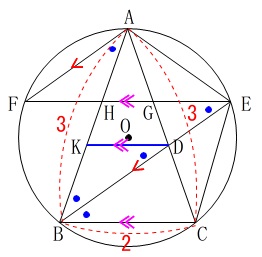二等辺三角形の性質から
　\(\,\mathrm{BK=KD=DC}\,\)
なのでこれを\(\,\color{blue}{x}\,\)とおくと、
　\(\,\mathrm{AK}=\color{blue}{3-x}\,\)
となります。

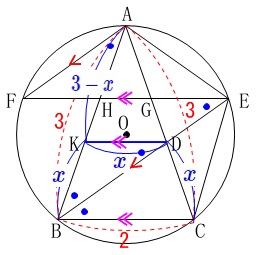
　\(\,\mathrm{△AKD}\,\)　∽　\(\,\mathrm{△ABC}\,\)
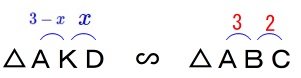なので、
　\(\begin{eqnarray}\displaystyle
(3-x):x&=&3:2\\
3x&=&2(3-x)\\
5x&=&6\\
x&=&\underline{　\frac{6}{5}　\mathrm{cm}}
\end{eqnarray}\)

補助線は平行線か垂線、ですね。

もう一つは\(\,\mathrm{AB}\,\)を\(\,\mathrm{BC}\,\)分だけ延長して、
と角の二等分線定理を証明する流れですが省略します。
　
②
線分\(\,\mathrm{DG}\,\)の長さを求めます。
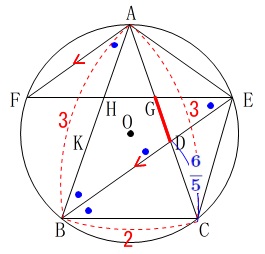この誘導問題がなければ③はかなりの難問になりますね。

(1)(2)の中で示していますが\(\,\mathrm{△AGE}\,\)は
　\(\,\mathrm{∠GAE=∠GEA}\,\)
の二等辺三角形なので
　\(\,\mathrm{AG=GE}\,\)
です。

　\(\begin{eqnarray}\displaystyle
\mathrm{AD}&=&\mathrm{AC-DC}\\
&=&3-\frac{6}{5}\\
&=&\frac{9}{5}
\end{eqnarray}\)

だから\(\,\mathrm{GD}=\color{magenta}{y}\,\)とすると
　\(\displaystyle \mathrm{AG=GE}=\color{magenta}{\frac{9}{5}-y}\)
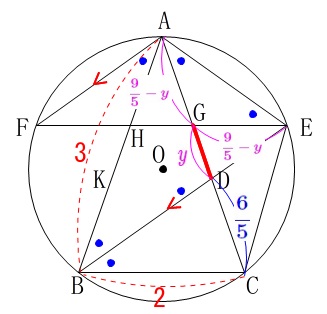(1)から\(\,\mathrm{△DBC}\,\)　∽　\(\,\mathrm{△DEG}\,\)
なので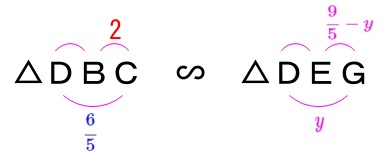
　\(\begin{eqnarray}\displaystyle
2:\left(\frac{9}{5}-y\right)&=&\frac{6}{5}:y\\
\frac{6}{5}\,\left(\frac{9}{5}-y\right)&=&2y\\
6(9-5y)&=&50y\\
54-30y&=&50y\\
-80y&=&-54\\
y&=&\frac{54}{80}\\
&=&\underline{　\frac{27}{40}　\mathrm{cm}}
\end{eqnarray}\)

\(\,2\,\)行目から\(\,3\,\)行目は両辺を\(\,25\,\)倍しています。
処理になれていない場合は一度展開してからで良いです。

③
\(\,\mathrm{△AFH}\,\)と\(\,\mathrm{△DBC}\,\)の面積比を求めます。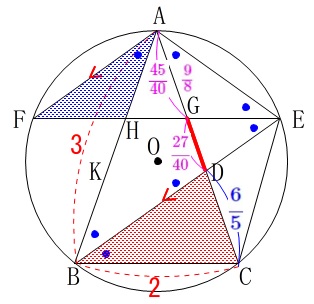
(2)で\(\,\mathrm{△AEG}\,\)≡\(\,\mathrm{△AFH}\,\)を証明しているので、
\(\,\mathrm{△AEG}\,\)と\(\,\mathrm{△DBC}\,\)の面積比を求めることと同じです。
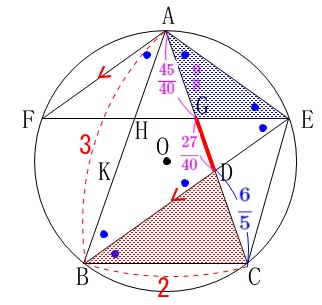何故三角形を換えてみるかというと、
線分比が出ているのが\(\,\mathrm{△AGE}\,\)側で、
(1)の相似が使えるからです。

②で\(\,\mathrm{DG}\,\)の長さを求めています。
　\(\hspace{4pt}\displaystyle \mathrm{DG}=\color{magenta}{\frac{27}{40}}\)

このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{AG}&=&\mathrm{AD-GD}\\
&=&\frac{9}{5}-\frac{27}{40}\\
&=&\frac{72-27}{40}\\
&=&\color{magenta}{\frac{45}{40}}=\color{magenta}{\frac{9}{8}}
\end{eqnarray}\)

約分しておいても良いのですが、
面積比を求めるときに分母が同じ方が何かと都合が良いので残しておきます。

\(\,\mathrm{△ABC}\,\)の面積を\(\,S\,\)とすると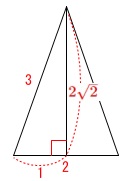
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times 2\times \color{red}{2\sqrt{2}}\\
&=&2\sqrt{2}
\end{eqnarray}\)
と具体的に求めることができるので、
部分部分の面積も具体的に求めることはできますが必要ありません。

比を求めれば良いので線分比を利用しましょう。
\(\,\mathrm{△ABC}\,\)を基準の\(\,S\,\)にします。

線分比を見ると
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:DC}&=&\frac{9}{5}:\frac{6}{5}\\
&=&\color{red}{3}:\color{red}{2}
\end{eqnarray}\)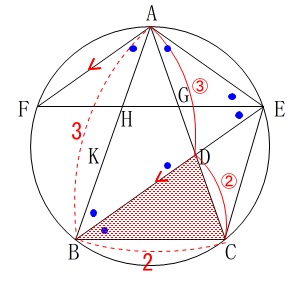なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△DBC}&=&\frac{2}{3+2}\times S\\
&=&\color{red}{\frac{2}{5}\,S}
\end{eqnarray}\)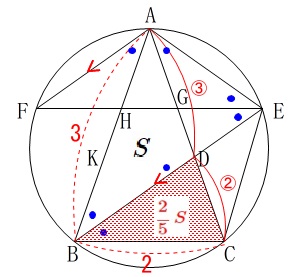
次に、
\(\,\mathrm{△DBC}\,\)∽\(\,\mathrm{△DEG}\,\)で相似比が
　\(\begin{eqnarray}\displaystyle
\mathrm{DC:DG}&=&\frac{6}{5}:\frac{27}{40}\\
&=&48:27\\
&=&\color{magenta}{16}:\color{magenta}{9}
\end{eqnarray}\)
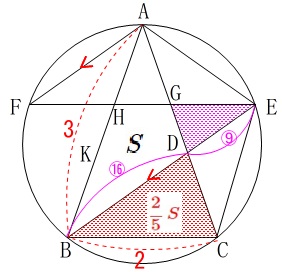相似比が\(\,16:9\,\)なので、
面積比は\(\,16^2:9^2\,\)になるから
　\(\begin{eqnarray}\displaystyle
\mathrm{△DEG}:\mathrm{△DEG}&=&16^2:9^2\\
256\times \mathrm{△DEG}&=&81\times \mathrm{△DBC}\\
\mathrm{△DBC}&=&\frac{81}{256}\times \mathrm{△DBC}\\
&=&\frac{81}{256}\times \frac{2}{5}\,S\\
&=&\color{magenta}{\frac{81}{128\times 5}\,S}
\end{eqnarray}\)

まだ先で約分できるかもしれないから分母の計算は残しておきます。
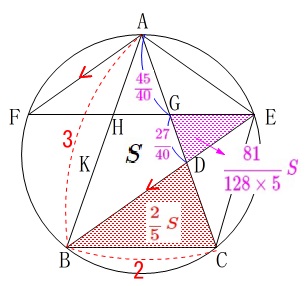次に\(\,\mathrm{△AEG}\,\)と\(\,\mathrm{△DEG}\,\)の比を出します。

　\(\begin{eqnarray}\displaystyle
\mathrm{AG:GD}&=&\frac{45}{40}:\frac{27}{40}\\
&=&\color{blue}{5}:\color{blue}{3}
\end{eqnarray}\)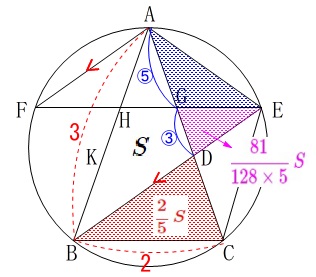このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{△AEG}&=&\frac{5}{3}\times \mathrm{△DEG}\\
&=&\frac{5}{3}\times \color{red}{\frac{81}{128\times 5}\,S}\\
&=&\color{blue}{\frac{27}{128}\,S}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AFH:△DBC}&=&\mathrm{△AEG:△DBC}\\
&=&\frac{27}{128}\,S:\frac{2}{5}\,S\\
&=&\underline{　135:256　}
\end{eqnarray}\)

見事な整数比ですね。
これって、②がなければなかなかたどり着かないでしょう。

(3)-②の別解

ちなみに、それぞれの線分比は同じ出し方をしたとして、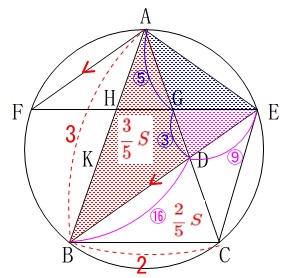
　\(\,\displaystyle \mathrm{△ABD}=\color{red}{\frac{3}{5}\,S}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{△AED}&=&\color{magenta}{\frac{9}{16}}\times \mathrm{\color{red}{△ABD}}\\
&=&\frac{9}{16}\times \frac{3}{5}\,S
\end{eqnarray}\)
さらに
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△AEG}}&=&\color{blue}{\frac{5}{3+5}}\times \mathrm{△AED}\\
&=&\frac{5}{8}\times \frac{9}{16}\times \frac{3}{5}\,S\\
&=&\frac{27}{128}\,S
\end{eqnarray}\)