2020年度三重県公立高校入試【前期】数学の問題と解説

2020年（令和2年）度に三重県で行われた公立高校入試前期学力検査の数学の問題と解説です。
問題は大きく５題ありますが基本が定着した人に取っては試験時間４５分は十分な時間です。
難問はありませんので、試験時間を十分に使って見直しの徹底で満点が狙えます。

2020年（令和2年）度三重県公立高校入試前期数学の問題と解説

\(\color{black}{\fbox{1}}\)の計算、作図の基本的な小問集合から、
\(\color{black}{\fbox{5}}\)の平面図形の面積比まで少し応用を含んだ問題構成となっています。

ここは問題の解説なので対策は詳しくしませんが、
基本中心の問題なので方針に迷う問題があるようなら基本からやり直しておきましょう。

2020年（令和2年）度三重県公立高校入試前期数学の問題

令和\(\,2\,\)年度三重県の県立高校入試前期選抜学力試験の数学の問題です。

⇒　2020年（令和２年）度三重県公立入試前期数学問題

基礎を重視した\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであります。

三重県の県立高校入試は各教科\(\,50\,\)点満点です。

2020年（令和2年）度三重県公立高校入試前期数学の解説

各問のポイントをおさえた解説をしていきますが、
基本問題が多いのでさっさと済ませます。

第１問基本的な計算が主な小問集合

\(\color{black}{\fbox{1}}\)

式の計算、方程式、作図などの基本\(\,10\,\)問があります。

(1)
　\(\hspace{10pt}(-3)^2+2\times (-5)\\
=9-10\\
=\underline{　-1　}\)

各項をていねいに、符号に注意して計算をすれば良いです。

(2)
　\(\hspace{10pt}\displaystyle \frac{4x-3}{2}-\frac{6x-7}{5}\\
=\displaystyle \frac{5(4x-3)-2(6x-7)}{10}\\
=\displaystyle \frac{20x-15-12x+14}{10}\\
=\displaystyle \underline{　\frac{8x-1}{10}　}\)

分母を1つにして、分子の計算に集中するのですが、
\(\,3\,\)行目は暗算せずに書き出した方がミスは減ります。

(3)
　\(\hspace{10pt}(-4xy)^2\times (-3x)\\
=16x^2y^2\times (-3x)\\
=\underline{　-48x^3y^2　}\)

計算力を見せつけて暗算したいでしょうが、
解答用紙に表現できるわけではないので、
確実に因数ごとに計算を進めると良いです。

暗算の方が早いと勘違いしている人が多いですが、
実際は遅いし、ミスも多いです。
（私は計算も遅いし、ミスも非常に多いですけど。）

(4)
連立方程式の処理の基本は一文字消去です。

　\(\begin{cases}
\hspace{4pt} 4x-3y=-7　･･･①\\
\hspace{4pt} 5x+9y=-13　･･･②
\end{cases}\)

消去する文字はどちらでも好きな方で良いです。
ここでは\(\,y\,\)を消去する方が楽なので\(\,y\,\)を消去します。

\(\,①\times 3+②\,\)です。
　\(\hspace{10pt}12x-9y=-21\\
\underline{+)\,5x+9y=-13}\\
\hspace{10pt}17x\hspace{10pt}\hspace{10pt}=-34\\
\hspace{40pt}x=-2\)

これを①か②にもどします。
どっちでも結果は同じです。

　\(\begin{eqnarray}\displaystyle
4(-2)-3y&=&-7\\
-8-3y&=&-7\\
-3y&=&-7+8\\
&=&1\\
y&=&-\frac{1}{3}
\end{eqnarray}\)

答え　\(\displaystyle \underline{　x=-2\,,\,y=-\frac{1}{3}　}\)

(5)
　\(\hspace{10pt}\displaystyle 5\sqrt{6}+2\sqrt{24}-\frac{6\sqrt{3}}{\sqrt{2}}\\
=5\sqrt{6}+4\sqrt{6}-3\sqrt{6}\\
=\underline{　6\sqrt{6}　}\)

実際にこの問題を解いたとき（見直し前）、
素因数分解もせず解いたときを再現してみましたが、
\(\,2\,\)行目は書き出します。
暗算の方が早いですか？

　\(\hspace{10pt}\displaystyle 5\sqrt{6}+2\sqrt{24}-\frac{6\sqrt{3}}{\sqrt{2}}\\
=\displaystyle 5\sqrt{6}+2\times 2\sqrt{6}-\frac{6\sqrt{3}\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}\\
=\displaystyle 5\sqrt{6}+4\sqrt{6}-\frac{6\sqrt{6}}{2}\\
=\displaystyle 9\sqrt{6}-3\sqrt{6}\\
=\underline{　6\sqrt{6}　}\)

計算処理する場所を作ってくれているのですから、
素因数分解、有理化は部分的にでも確実に計算した方が良いです。

「たかが計算ミス１問くらい」、
と他の問題でカバーしようとしている人、
あなたと君と、あなたはだーれ？そこの人です。
試験結果がどうなろうと私には関係ないけど、
この問題は\(\color{black}{\fbox{5}}\)の最終問題も同じ配点です。
今回は最終問題が簡単だったからそれほど差はありませんが、
試験時間は限られていて、試験結果は点数で出るのですよ。

全体通じて注意しておきたいことは他にもありますが、
会員は『最大得点獲得法』には必ず目を通して受験するようにしてください。

あ、ここは解説でした。
対策が分からないときはお問合せ下さい。

(6)
方程式を解くときの基本は何次方程式でも右辺を\(\,0\,\)にするように、
左辺にすべての項を集めることです。

　\(\begin{eqnarray}\displaystyle
(x+4)(x-6)&=&6x-39\\
x^2-2x-24&=&6x-39\\
x^2-8x+15&=&0\\
(x-3)(x-5)&=&0\\
x&=&\underline{　3\,,\,5　}
\end{eqnarray}\)

途中、移項などは暗算しています。
行間を自分でうめてください。

※
\(\,1\,\)次方程式や平方根型\(\,2\,\)次方程式を処理するときは、
右辺に定数を残した方が早い場合がありますが、
例外だと思っておけば高校でも方程式の処理は同じです。

なんだか長くなる気がしてきたので急ぎます。

(7)
変化の割合です。
　\(\displaystyle (\,変化の割合\,)=\frac{　(\,y\,の増加量\,)　}{　(\,xの増加量\,)　}\)

関数\(\,y=ax^2\,\)において
　\(\hspace{4pt}(\,\color{red}{-5}\,,\,\color{red}{25a}\,)\)
　\(\hspace{4pt}(\,\color{blue}{-3}\,,\,\color{blue}{9a}\,)\)
この\(\,2\,\)点の変化の割合が\(\,2\,\)なので
　\(\begin{eqnarray}\displaystyle
\frac{\color{blue}{9a}-\color{red}{25a}}{\color{blue}{-3}-(\color{red}{-5})}&=&2\\
\frac{-16a}{2}&=&2\\
-16a&=&4\\
a&=&\underline{　-\frac{1}{4}　}
\end{eqnarray}\)

増加量を計算するとき引く方向は、
\(\,x,y\,\)で同じにすることに注意ですね。

(8)
円すいの体積です。
　\(\displaystyle (すい体の体積)=\frac{1}{3}\times (底面積)\times (高さ)\)

円すいの底面半径と高さが与えられています。
　底面の半径\(\,\mathrm{5\,cm}\,\)
　高さが\(\,\mathrm{6\,cm}\,\)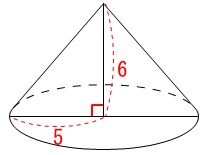底面の円の面積は
　\(\hspace{10pt}\pi\,(5)^2=25\,\pi　\mathrm{cm^2}\)
なので求める円すいの体積を\(\,V\,\)とすると
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 25\,\pi\times 6\\
&=&\underline{　50\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

すい体の体積は柱体の\(\,\displaystyle \frac{1}{3}\,\)です。
知ってはいても、忘れることないですか？

(9)
\(\,\mathrm{∠BEC}\,\)の大きさを求めます。

条件
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{CE}\,\)は\(\,\mathrm{∠ACD}\,\)の二等分線
　\(\,\mathrm{∠BAC=40^{\circ}}\,\)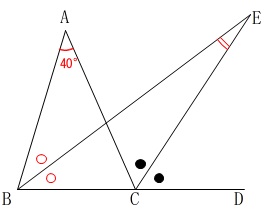\(\,\color{red}{○}\,\)や\(\,●\,\)は具体的には求まりません。

一般的に成り立つ関係式から求めることになりますが、
一般的に成り立つなら具体的にも成り立たなくてはならないので、
　\(\,\mathrm{∠ABC=80^{\circ}}\,\)
とすると、（仮において）
　\(\,\mathrm{∠ABE=∠DBE=\color{red}{40^{\circ}}}\,\)

三角形の1つの外角になるので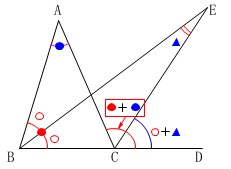
　\(\begin{eqnarray}\displaystyle
\,\mathrm{∠ACD}&=&40^{\circ}+80^{\circ}\\
&=&120^{\circ}
\end{eqnarray}\)
だから
　\(\,\mathrm{∠ACE=∠DCE=\color{blue}{60^{\circ}}}\,\)

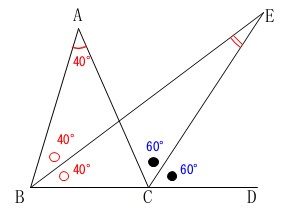
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠DBE+∠BEC}&=&\mathrm{∠DCE}\\
40^{\circ}+\mathrm{∠BEC}&=&60^{\circ}\\
\mathrm{∠BEC}&=&60^{\circ}-40^{\circ}\\
&=&\underline{　20^{\circ}　}
\end{eqnarray}\)

求め方を聞かれた場合にこれでは通用しないので、
一般的に成り立たせておきます。

　\(\,\mathrm{∠ABE=∠DBE}=\color{red}{a}\,\)
　\(\,\mathrm{∠ACE=∠DCE}=\color{blue}{b}\,\)
とすると、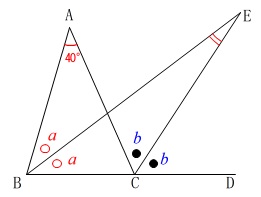三角形の1つの外角は他の2つの内角の和になるので、
\(\,\mathrm{△ABC}\,\)において
　\(\mathrm{∠ACD=∠ABC+∠BAC}\)
なので
　\(\begin{eqnarray}\displaystyle
2\,b&=&2\,a+40^{\circ}\\
\color{blue}{b}&=&\color{blue}{a}+20^{\circ}　･･･①\\
\end{eqnarray}\)
また、
\(\,\mathrm{△BCE}\,\)において
　\(\mathrm{∠DCE=∠CBE+∠BEC}\)
なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{b}&=&\color{red}{a}+\mathrm{∠BEC}　･･･②
\end{eqnarray}\)

①②から
　\(\,\mathrm{∠BEC}=\underline{　20^{\circ}　}\,\)

角度の関係を文字で表すのは良くある問題なので慣れておいた方が良いです。

(10)
\(\,\mathrm{∠APB=120^{\circ}}\,\)となるひし形\(\,\mathrm{AQBP}\,\)を作図します。

線分\(\,\mathrm{AB}\,\)はひし形の対角線になるので、
\(\,\mathrm{AB}\,\)の垂直二等分線上に\(\,\mathrm{P,Q}\,\)はあります。

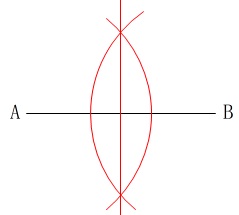
後は\(\,\mathrm{∠APB}\,\)を\(\,120°\,\)にすることを考えます。

\(\,\mathrm{∠APB=120°}\,\)のとき\(\,\mathrm{∠APQ=60°}\,\)なので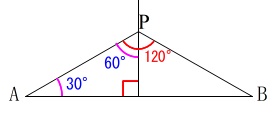
\(\,\mathrm{∠PAB=30^{\circ}}\,\)となる線を作図します。

\(\,90°,45°,22.5°\,\)は垂線からですが、
（\(\,90°\,\)は直径の円周角利用も良くあります。）
\(\,30°,60°,120°,150°\,\)は正三角形からです。

\(\,1\,\)辺が\(\,\mathrm{AB}\,\)の正三角形作ると\(\,60°\,\)ができるので、
その角の二等分線を引けば\(\,\color{magenta}{30°}\,\)が作図できます。
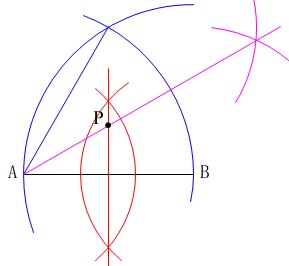\(\,\mathrm{Q}\,\)は\(\,\mathrm{P}\,\)と同じ手順で\(\,\mathrm{AB}\,\)の下側に描くか、
\(\,\mathrm{P}\,\)を\(\,\mathrm{AB}\,\)を軸に対称移動すれば決まります。
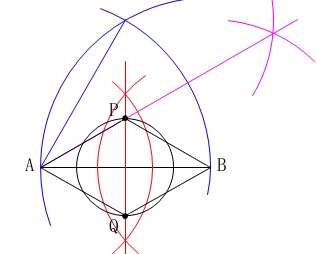お気づきの通り、
上下で同じことを繰り返すならいっそ同時にやれば良いですよね。
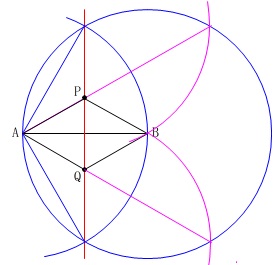半径\(\,\mathrm{AB}\,\)の円を利用しています。

ひし形の作図は\(\,2019\,\)年の三重県の後期でもありました。

第２問データの活用と確率

\(\color{black}{\fbox{2}}\)

データの活用と確率です。

(1)
代表値の問題です。

①
最頻値を求めます。

\(\color{black}{\fbox{(ｱ)}}\)と\(\color{black}{\fbox{(ｲ)}}\)を除いた度数合計が、
　\(\hspace{10pt}2+3+8+5+4\\
=22\)

度数合計\(\,29\,\)から残り\(\,7\,\)人であることを考えて度数が
　\(\,6\,\)以上\(\,8\,\)未満の階級の度数\(\,8\,\)
以上になる階級はありません。

よって最頻値は
　\(\,6\,\)以上\(\,8\,\)未満の階級の階級値
なので
　\(\hspace{10pt}\displaystyle \frac{6+8}{2}=\underline{　7　点}\)

②
中央値が含まれる階級と、
最頻値が含まれる階級が異なるとき、
\(\color{black}{\fbox{(ｱ)}}\)に当てはまる数を求めます。

最頻値が含まれる階級は
　\(\,6\,\)以上\(\,8\,\)未満の階級
と、分かっています。

\(\,29\,\)人のデータの中央値は、
小さい方から\(\,15\,\)番目の人の値になります。

小さい方から\(\,15\,\)番目の人が
　\(\,6\,\)以上\(\,8\,\)未満の階級
にならなければ良いのです。

\(\color{black}{\fbox{(ｱ)}}\)と\(\color{black}{\fbox{(ｲ)}}\)を合わせて\(\,7\,\)人なので
\(\color{black}{\fbox{(ｱ)}}\)に当てはまるのは\(\,0\,\)から\(\,7\,\)のうち
　\(\hspace{10pt}\underline{　0\,または\,1　}\)

\(\color{black}{\fbox{(ｲ)}}\)より大きい方の階級で\(\,9\,\)人います。
中央値が最頻値と異なるためには、
　\(\,8\,\)以上\(\,10\,\)未満の階級
に中央値がなければりません。
（大きい方からの度数の合計が\(\,15\,\)以上）

\(\color{black}{\fbox{(ｱ)}}\)との合計が\(\,7\,\)だから
\(\color{black}{\fbox{(ｲ)}}\)は\(\,6\,\)か\(\,7\,\)でなければならないので、
\(\color{black}{\fbox{(ｱ)}}\)にあてはまるのは
　\(\hspace{10pt}\underline{　1\,または\,0　}\)

と、逆に行った方が調べるには早いです。
どっちでも良いので先に進みます。

(2)
\(\,6\,\)枚のカードを取り出して、もどすときの確率です。

条件
　カードは\(\,1\,\)から\(\,6\,\)の数字が記入された\(\,1\,\)枚ずつ
　\(\,1\,\)回目取り出したカードの数字を\(\,x\,\)
　\(\,2\,\)回目取り出したカードの数字を\(\,y\,\)
　点\(\,\mathrm{P}\,\)を座標\(\,(\,x\,,\,y\,)\,\)とする。

\(\,6\,\)枚のカードは\(\,1,2,3,4,5,6\,\)なのでさいころと同じです。
樹形図でも表でもどちらでも良いです。

①
点\(\,\mathrm{P}\,\)が関数\(\,y=x\,\)のグラフ上にある確率です。

\(\,x=y\,\)つまり\(\,1\,\)回目と\(\,2\,\)回目の数字が同じ確率なので
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5 & 6\\ \hline
1 & ○ & & & & & \\ \hline
2 & & ○ & & & & \\ \hline
3 & & & ○ & & & \\ \hline
4 & & & & ○ & & \\ \hline
5 & & & & & ○ & \\ \hline
6 & & & & & & ○\\ \hline
\end{array}\)

　\(\hspace{10pt}\displaystyle \frac{6}{36}=\underline{　\frac{1}{6}　}\)

②
点\(\,\mathrm{P}\,\)が関数\(\displaystyle \,y=\frac{8}{x}\,\)のグラフ上にある確率です。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{8}{x}\\
xy&=&8
\end{eqnarray}\)
なので
　\(\,1\,\)回目の数字と\(\,2\,\)回目の数字の積が\(\,8\,\)
になる確率です。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5 & 6\\ \hline
1 & & & & & & \\ \hline
2 & & & & ● & & \\ \hline
3 & & & & & & \\ \hline
4 & & ● & & & & \\ \hline
5 & & & & & & \\ \hline
6 & & & & & & \\ \hline
\end{array}\)

　\(\hspace{10pt}\displaystyle \frac{2}{36}=\underline{　\frac{1}{18}　}\)

③
点\(\,\mathrm{P}\,\)が関数\(\displaystyle \,y=\frac{a}{x}\,\)のグラフ上にある確率が、
\(\displaystyle \frac{1}{9}\,\)になる\(\,a\,\)をすべて求めます。

　\(\hspace{10pt}\displaystyle \frac{1}{9}=\frac{4}{36}\)
なので
　\(\,xy=\color{red}{a}\,\)
つまり、
　\(\,1\,\)回目の数字と\(\,2\,\)回目の数字の積が同じ数字\(\,\color{red}{a}\,\)
となる\(\,(\,x\,,\,y\,)\,\)の組が
　\(\,36\,\)組中\(\,4\,\)組ある数字\(\,\color{red}{a}\,\)
をすべて求めれば良いのです。

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
1 & 1 & 2 & 3 & 4 & 5 & \color{red}{6} \\ \hline
2 & 2 & 4 & \color{red}{6} & 8 & 10 & \color{blue}{12}\\ \hline
3 & 3 & \color{red}{6} & 9 & \color{blue}{12} & 15 & 18 \\ \hline
4 & 4 & 8 & \color{blue}{12} & 16 & 20 & 24\\ \hline
5 & 5 & 10 & 15 & 20 & 25 & 30\\ \hline
6 & \color{red}{6} & \color{blue}{12} & 18 & 24 & 30 & 36\\ \hline
\end{array}\)

答え　\(\,a=\underline{　6\,,\,12　}\,\)

積が\(\,1,4,9,16,25,36\,\)になる組を軸として対称になっているので、
軸で切った半分に2つ同じ数字が出てくれば良いのですが、別に気にしなくて良いです。

第３問１次関数

水そうにたまる水の高さと時間との関係、
\(\,1\,\)次関数の問題です。

水そうの下に直方体が固定されていて、
水は一定の割合で入れられますが途中で高さの変化が変わります。

条件
　面\(\,\mathrm{ABCD}\,\)を底面とする直方体があり、
　大きさは縦\(\,60\,\)、横\(\,30\,\)、高さ\(\,40\,\)
　面\(\,\mathrm{PQRS}\,\)を底面とする水そうがあり、
　大きさは縦\(\,60\,\)、横\(\,80\,\)、高さ\(\,60\,\)
　水は入れ始めて\(\,1\,\)分後\(\,4\,\)になった。
　入れ始めてからの時間\(\,x\,\)分、水の高さ\(\,y\,\)とする。
（長さは\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。）
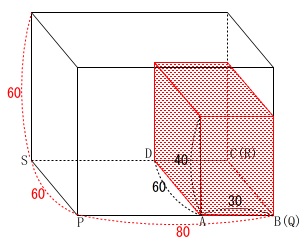高さを見るときは立体で見なくて良いです。

(1)
高さ\(\,y\,\)が\(\,24\,\)になるときの時間\(\,x\,\)を求めます。

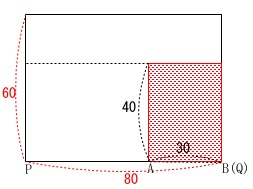
水の高さは\(\,1\,\)分間に\(\,4\,\)上昇するので
底面\(\,\mathrm{ABCD}\,\)の直方体の高さ\(\,40\,\)を超える\(\,10\,\)秒までは
　\(\hspace{4pt}y=4x　(\,0\,≦\,x\,≦\,10\,)\)

よって、
　\(\begin{eqnarray}\displaystyle
24&=&4x\\
x&=&\underline{　6　}(適)
\end{eqnarray}\)

(2)
条件から\(\,1\,\)分間に底面\(\,\mathrm{PADS}\,\)で\(\,4\,\)上昇するので、
底面\(\,\mathrm{PADS}\,\)の面積が
　\(60\times 50=3000\)
だから\(\,1\,\)分間に入る水の量は
　\(3000\times 4=12000\)

\(\,12\,\)分では
　\(\hspace{10pt}12000\times 12\\
=\underline{　144000　\mathrm{cm^3}}\)

入る水の量は一定なので、
高さは変わっても量は一定で増えます。

(3)
水がたまる部分は水そうから直方体を引けば良いので、
水そうの体積（底面積\(\,\color{magenta}{4800}\,\)）
　\(\hspace{10pt}60\times 80\times 60\\
=288000\)
直方体の体積（底面積\(\,\color{blue}{3000}\,\)）
　\(\hspace{10pt}60\times 30\times 40\\
=72000\)
から
　\(\hspace{10pt}288000-72000\\
=216000\)

\(\,1\,\)分間に入る水の量は\(\,12000\,\)だから
　\(\hspace{10pt}\displaystyle \frac{216000}{12000}=\frac{216}{12}\\
=\underline{　18　分}\)
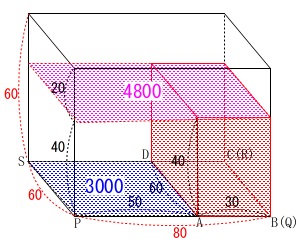底面の面積が変わる直方体を超えるまでに\(\,10\,\)分、
その後水そうがいっぱいになるまで\(\,8\,\)分かかるということです。

(4)
途中で底面積が広くなるので\(\,1\,\)分あたりの水の上昇は小さくなります。
関数を表すグラフの傾きが小さくなるということです。

答え　\(\,\underline{　イ　}\,\)

(5)
時間と水面の高さの関係式なので\(\,2\,\)点を書き出しましょう。

水面の高さが\(\,40\,\)になるのは\(\,10\,\)分後だから
　\(\hspace{4pt}(\,10\,,\,40\,)\)
満水になるときの高さ\(\,60\,\)になるのは\(\,18分\,\)後だから
　\(\hspace{4pt}(\,18\,,\,60\,)\)

これら\(\,2\,\)点を通る直線です。

答え　\(\,\displaystyle y=\frac{5}{2}\,x+15\,\)

\(\,2\,\)点を通る直線が求められない場合は、
一日かけてでも求められるようになっておきましょう。
傾きから求める方法で良いです。

第４問相似比と方程式の処理

円すいの相似比と体積比および方程式の変形についての問題です。

(1)
円すいを底面と平行な面で等間隔で切った体積を求める問題です。

条件
　底面の直径が\(\,\mathrm{AB}\,\)の円すいがある。
　底面に平行な面\(\,\mathrm{L,M}\,\)で円すいを等間隔で3つに切る。
　切り分けられた立体を上から\(\,\mathrm{P,Q,R}\,\)とする。
　\(\,\mathrm{Q}\,\)の体積が\(\,28\,\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）
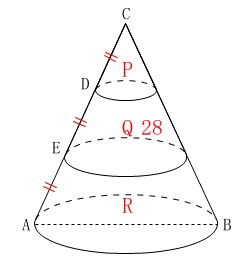頂点\(\,\mathrm{C}\,\)とする円すいが3つあります。
\(\,\mathrm{ＣＤ=ＤＥ=ＥＡ}\,\)なので円すいだけでみると
　相似比は\(\,1:2:3\,\)
　体積比は\(\,1^3:2^3:3^3=1:8:27\,\)
となるので、立体\(\,\mathrm{P,Q,R}\,\)の体積比は
　\(\,\mathrm{P:Q:R=1:7:19}\,\)
です。

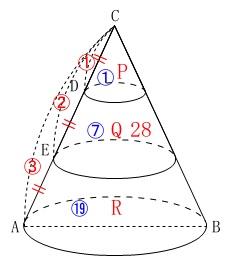
\(\,\mathrm{Q}\,\)の体積が\(\,28\,\)なので、
　\(\begin{eqnarray}\displaystyle
7:19&=&28:\mathrm{Q}\\
7\times \mathrm{Q}&=&28\times 19\\
\mathrm{Q}&=&\underline{　76　\mathrm{cm^3}}
\end{eqnarray}\)

円すいの体積比\(\,\mathrm{P:Q:R=1:8:27}\,\)のとき
\(\,\mathrm{Q}\,\)の体積は上の\(\,\mathrm{P}\,\)の部分を除くので
　\(\hspace{4pt}8-1=7\)
\(\,\mathrm{R}\,\)の体積は上の\(\,\mathrm{P,Q}\,\)を除くことになるので
　\(\hspace{4pt}27-8=19\)
の比になることは確認しておいてください。

(2)
\(\,2\,\)次方程式を解くときの処理についての注意点です。

　\(\begin{eqnarray}\displaystyle
3(x^2-8)&=&(x-8)(x+3)\\
3x^2-24&=&x^2-5x-24\\
2x^2+5x&=&0\\
x(2x+5)&=&0\\
x&=&0\,,\,-\frac{5}{2}
\end{eqnarray}\)

とするのが正しい処理です。

①
方程式の処理として正しくないものを選びます。

答え　\(\,\underline{　ウ　}\,\)

②
①で選んだ処理が正しくない理由を書きます。

手順で
　\(\begin{eqnarray}\displaystyle
2x^2+5x&=&0\\
2x+5&=&0
\end{eqnarray}\)
としているところが正しくない処理です。

両辺を\(\,x\,\)で割っていることです。

\(\,x≠0\,\)（\(\,x\,\)が\(\,0\,\)でない）という条件があれば、
解を求めるということに関して間違いではありません。

ただし、この場合は\(\,x≠0\,\)という条件はありません。
ということは\(\,x=0\,\)の可能性もあるので割ることができません。

算数でも数学でも\(\,0\,\)で割るということはできません。

理由を書くとすると、
　「\(\,x=0\,\)の場合、両辺を\(\,x\,\)で割ることはできないから。」

あまり詳しくすると余計分からなくなるかもしれないけど、
上の\(\,2\,\)次方程式の解
　\(\displaystyle \hspace{4pt}x=0\,,\,-\frac{5}{2}\)
は、
　\(\,x=0\,\)または\(\displaystyle \,x=-\frac{5}{2}\,\)
です。

\(\,x=0\,\)も方程式の解なので都合良く無くしてしまってはいけません。

第５問平面図形の総合問題

合同の証明から線分比や面積比の平面図形の問題です。

条件
　\(\,\mathrm{BD:DC=1:2}\,\)
　\(\,\mathrm{E}\,\)は\(\,\mathrm{AD}\,\)の中点
　\(\,\mathrm{F}\,\)は\(\,\mathrm{AC}\,\)の中点
　\(\,\mathrm{FG}\,\)∥\(\,\mathrm{AD}\,\)
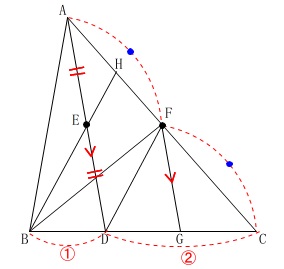中点連結定理からほとんどのことが見えてきますが問題に従って進めます。

(1)
\(\,\mathrm{△BDE}\,\)≡\(\,\mathrm{△DGF}\,\)であることを証明します。
\(\,\mathrm{FG}\,\)∥\(\,\mathrm{AD}\,\)
なので　
　\(\,\mathrm{CF:FA=CG:GD=1:1}\,\)
このことから\(\,\mathrm{G}\,\)は\(\,\mathrm{ＣＤ}\,\)の中点です。

これにより
　\(\,\mathrm{BD=DG=GC}\,\)

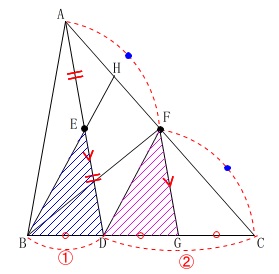
また中点連結定理から
　\(\displaystyle \,\mathrm{FG=\frac{1}{2}AD}\,\)
さらに\(\,\mathrm{E}\,\)は\(\,\mathrm{AD}\,\)の中点なので
　\(\displaystyle \mathrm{ED=\frac{1}{2}AD}\)
このことから
　\(\hspace{4pt}\mathrm{ED=FG}\)
がいえます。

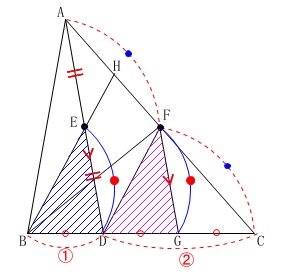
また、\(\,\mathrm{FG}\,\)∥\(\,\mathrm{AD}\,\)なので同位角が等しく
　\(\,\mathrm{∠BDE=∠DGF}\,\)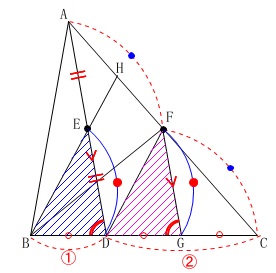合同条件がそろったので後は証明するだけです。

さらに、\(\,\mathrm{E,F}\,\)が\(\,\mathrm{AD,AC}\,\)の中点なので、
\(\,\mathrm{EF}\,\)は\(\,\mathrm{BC}\,\)に平行になります。
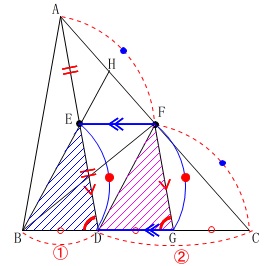四角形\(\,\mathrm{BDFE}\,\)と四角形\(\,\mathrm{DGFE}\,\)が平行四辺形なので、
　\(\mathrm{EB=FD}\)
も言えるので、\(\,3\,\)辺相等条件から
　\(\mathrm{△BDE}\)≡\(\,\mathrm{△DGF}\,\)≡\(\,\mathrm{△FED}\,\)
となります。

証明は好きな条件を使ってやっておいてください。
中点連結定理で言えることを並べていれば、
合同条件を外すことはないでしょう。

証明する、線分比を出す、面積比を出すだけなら
与えられた条件が多すぎてどれを利用するか迷いますね。

(2)
線分\(\,\mathrm{BE}\,\)と線分\(\,\mathrm{EH}\,\)の長さの比を求めます。
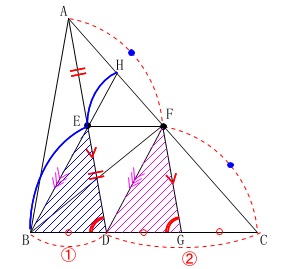\(\,\mathrm{△HEF}\,\)∽\(\,\mathrm{△HBC}\,\)で相似比が\(\,1:3\,\)を利用してもいいし、
\(\,\mathrm{△CDF}\,\)∽\(\,\mathrm{△CBH}\,\)で相似比\(\,2:3\,\)を利用しても良いです。

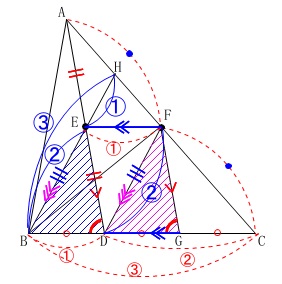
　\(\hspace{4pt}\mathrm{BE:EH}=\underline{　2:1　}\)

(3)
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DGF}\,\)の面積比を求めます。
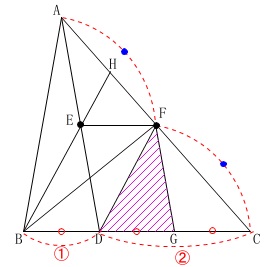\(\,\mathrm{△ABC}\,\)を\(\,S\,\)として、(\(\,S=1\,\)でも良いです。）
\(\,\mathrm{△DGF}\,\)を\(\,S\,\)で表します。

(1)の合同を利用すると、
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△BDE}\,\)の面積比を求めることになります。

\(\,\mathrm{BD:DC=1:2}\,\)なので
　\(\hspace{4pt}\displaystyle \mathrm{△ABD}=\frac{1}{3}\times \mathrm{△ABC}\)

\(\,\mathrm{AE:ED=1:1}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△BDE}&=&\mathrm{△DGF}\\
&=&\frac{1}{2}\times \mathrm{△ABD}\\
&=&\frac{1}{2}\times \frac{1}{3}\times \mathrm{△ABC}\\
&=&\frac{1}{6}\times \mathrm{△ABC}
\end{eqnarray}\)

よって、
　\(\,\mathrm{△ABC:△DGF=\underline{　6:1　}}\,\)

または、(1)の合同を利用しなくても
　\(\mathrm{BD:DC=1:2}\)
高さは同じなので
　\(\displaystyle \,\mathrm{△ADC}=\frac{2}{3}\,S\,\)

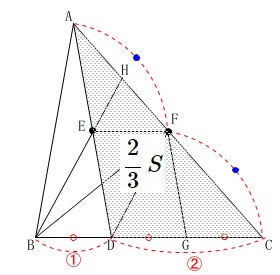
\(\,\mathrm{△ADC}\,\)の底辺を\(\,\mathrm{AC}\,\)と見ると
　\(\mathrm{AF:CF=1:1}\)
高さは同じなので
　\(\begin{eqnarray}\displaystyle
\mathrm{△CDF}&=&\frac{1}{2}\,\mathrm{△ADC}\\
&=&\frac{1}{2}\times \frac{2}{3}\,S\\
&=&\frac{1}{3}\,S
\end{eqnarray}\)
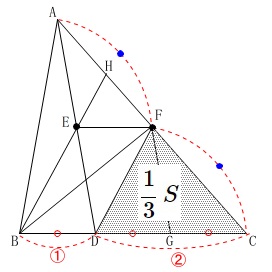さらに、\(\,\mathrm{△CDF}\,\)において底辺を\(\,\mathrm{DC}\,\)と見ると
　\(\mathrm{DG:GC=1:1}\)
高さは同じなので
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGF}&=&\frac{1}{2}\times \mathrm{△CDF}\\
&=&\frac{1}{2}\times \frac{1}{3}\,S\\
&=&\frac{1}{6}\,S
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC:△DGF}&=&S:\frac{1}{6}\,S\\
&=&\underline{　6:1　}
\end{eqnarray}\)

線分比で圧縮していくのに慣れている人は
　\(\begin{eqnarray}\displaystyle
\mathrm{△DGF}&=&\frac{2}{3}\times \frac{1}{2}\times \frac{1}{2}\times \mathrm{△ABC}\\
&=&\frac{1}{6}\times\mathrm{ △ABC}
\end{eqnarray}\)
で良いですよ。

(4)
\(\,\mathrm{△AHI}\,\)と\(\,\mathrm{△GFH}\,\)の面積の和が\(\,\mathrm{△DGI}\,\)の面積の\(\,\mathrm{3}\,\)倍になるとき、
線分\(\,\mathrm{AI}\,\)の長さを\(\,\mathrm{FG}\,\)の長さを用いて表します。
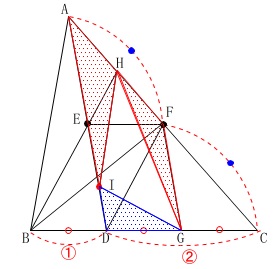加わる条件はありませんが、
　\(\,\mathrm{FG}=\color{red}{a}\,\)
を用いて\(\,\mathrm{AI}\,\)の長さを求めます。

\(\,\mathrm{AD＝2ED}\,\)で\(\,\mathrm{ED=FG}\,\)なので
　\(\,\mathrm{AD}=2a\,\)

\(\,\mathrm{AI}=x\,\)とすると\(\,\mathrm{ID}=2a-x\,\)
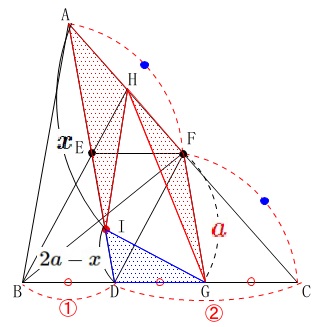\(\,\mathrm{HB}\,\)∥\(\,\mathrm{FD}\,\)で\(\,\mathrm{CF:FH=2:1}\,\)だから、
\(\,\mathrm{AF=FC}\,\)なので\(\,\mathrm{AH=HF}\,\)
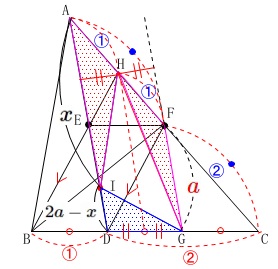比なので高さを具体的な数値ではなく比で表します。

\(\,\mathrm{AD}\,\)と\(\,\mathrm{FG}\,\)との距離を高さ\(\,\color{red}{2}\,\)とすると、
　\(\,\mathrm{△DGI}\,\)の底辺を\(\,\mathrm{DI}\,\)と見ると高さは\(\,\color{red}{2}\,\)
　\(\,\mathrm{△AHI}\,\)の底辺を\(\,\mathrm{AI}\,\)と見ると高さは\(\,\color{red}{1}\,\)
　\(\,\mathrm{△GFH}\,\)の底辺を\(\,\mathrm{FG}\,\)と見ると高さは\(\,\color{red}{1}\,\)
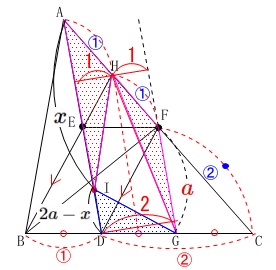非常に見にくいですが、笑
高さの比がわかれば単なる方程式なので簡単に済ませて終わりにします。
　\(\hspace{10pt}\mathrm{△AHI+△GFH}\\
\displaystyle =\frac{1}{2}\times x\times \color{red}{1}+\frac{1}{2}\times a\times \color{red}{1}\\
\displaystyle =\frac{1}{2}(x+a)\)

　\(\hspace{10pt}\mathrm{△DGI}\\
\displaystyle =\frac{1}{2}\times (2a-x)\times \color{red}{2}\\
=2a-x\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AHI+△GFH}&=&3\times \mathrm{△DGI}\\
\frac{1}{2}(x+a)&=&3\times (2a-x)\\
x+a&=&6(2a-x)\\
&=&12a-6x\\
7x&=&11a\\
x&=&\underline{　\frac{11}{7}\,a　\mathrm{cm}}
\end{eqnarray}\)

\(\,\mathrm{△GFH}\,\)は\(\,\mathrm{△ABC}\,\)の\(\,\displaystyle \frac{1}{12}\,\)と分かるのですが、
\(\,\mathrm{I}\,\)の位置が固定されえていないので\(\,\mathrm{△ABC}\,\)を基準にするのをやめました。

ただ、中点連結定理を使うと線分比がきれいに出てきます。
これを最初に済ませておけば各問題が別々に解決できました。

条件がすぎるほどあったのでたまには良いでしょう。
時間も十分だったはずなので(3)の面積比も(1)の合同を使わずに求めておきました。

ただ、普通は(1)(2)\(\cdots\)とあれば、
前に証明したことなどは利用するように問題は作られることが多いので気にはしておいてください。

以上です。

⇒　2020年度後期（近日公開予定ですが遅くなったら済みません。すでに遅いけど。）

\(\,2019\,\)年度の後期選抜では誘導に乗れないと厳しい問題がありましたが、
\(\,2020\,\)年度はどうでしょう。

誘導無しで最後までいける作業をしているかどうかで差が出てきます。

⇒　三重県公立高校入試の数学の問題と解説

三重県の県立入試は基本重視です。
差がつくのは、思考力ではなく、作業量ですね。