2020年(令和2年)度三重県公立高校入試後期の数学問題と解説

2020年に行われた令和2年度三重県公立高校入試後期選抜試験の数学の問題と解説です。
問題は大きく5問の構成で、基本重視のバランスの良さも例年通り通りです。
差がつくと予想され詳しく解説が必要なのは5問目ですが、
ちょっとした発展公式で解法とかかる時間に大きく差が出ます。

2020年(令和2年)度三重県公立高校入試後期の数学問題と解説

平均点は昨年度より若干上がりました。
やはり\(\color{black}{\fbox{5}}\)で差がつきやすいと思われますが、
しっかり基本を抑えておけば\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{4}}\)で十分合格点は取れる問題構成です。

2020年(令和2年)度三重県立高校入試の後期数学問題

令和2年度三重県立後期高校入試の問題

⇒　令和2年度三重県立高校入試の後期数学問題

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであり、試験時間は\(\,45\,\)分です。

2020年(令和2年)度三重県立高校入試の後期数学の解説

いつも長くなるのでできるだけ簡潔にまとめます。

第１問基本の計算小問集合

\(\color{black}{\fbox{1}}\)
式の計算から方程式データの活用計算問題が\(\,7\,\)問あります。

(1)
　\(\hspace{10pt}(-9)\times 7\\
=\underline{　-63　}\)

解説は不要でしょう。
マイナスの符号だけは忘れないようにしましょう。

(2)
　\(\hspace{10pt}\displaystyle \frac{4}{5}x-\frac{3}{4}x\\
\displaystyle =\frac{16x-15x}{20}\\
\displaystyle =\underline{　\frac{x}{20}　}\)

この計算式の\(\,x\,\)は分子にあります。
答えは\(\displaystyle \underline{　\frac{1}{20}\,x　}\)でも良いですよ。

(3)
　\(\hspace{10pt}7(a-b)-4(2a-8b)\\
=7a-7b-8a+32b\\
=\underline{　-a+25b　}\)

マイナスの展開は符号注意です。

(4)
　\(\hspace{10pt}(\sqrt{5}-\sqrt{2})^2\\
=5-2\sqrt{10}+2\\
=\underline{　7-2\sqrt{10}　}\)

暗算してミスするよりは確実に公式展開しましょう。
公式を利用せず展開してもそれほど時間の差はありません。

(5)
　\(\hspace{10pt}x^2-36\\
=x^2-6^2\\
=\underline{　(x+6)(x-6)　}\)

平方の差を、和と差の積にする因数分解です。

(6)
　\(\hspace{10pt}x^2+5x-1=0\)
因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot 1\cdot (-1)}}{2}\\
&=&\frac{-5\pm \sqrt{25+4}}{2}\\
&=&\underline{\frac{　-5\pm \sqrt{29}}{2}　}
\end{eqnarray}\)

(7)
\(\,4\,\)月から\(\,9\,\)月までの\(\,6\,\)ヶ月の平均が\(\,5.5\,\)冊なので、
\(\,6\,\)ヶ月間に借りた冊数は
　\(\hspace{4pt}5.5\times 6=\color{red}{33}　冊\)

\(\,8\,\)月を除いて借りた札数合計が\(\,\color{blue}{24}\,\)冊なので
　\(\hspace{10pt}n=\color{red}{33}-\color{blue}{24}=\underline{　9　}\)

\(\,n\,\)の数値を答えるだけなので単位は必要ないです。

第２問１次関数と方程式不等式と確率の小問集合

\(\color{black}{\fbox{2}}\)
(1)
\(\,1\,\)次関数による費用問題です。

　\(\,\mathrm{A}\,\)：\(\,1\,\)冊\(\,1250\,\)円、初期費用\(\,0円\,\)
　\(\,\mathrm{B}\,\)：\(\,1\,\)冊\(\,600\,\)円、初期費用\(\,18000\,\)円

作成する冊数を\(\,x\,\)、総費用\(\,y\,\)がなっています。
関数にしておくと
　\(\,\mathrm{A}\,\)：\(y=1250x\)
　\(\,\mathrm{B}\,\)：\(y=600x+18000\)

①
\(\,\mathrm{B}\,\)で\(\,15\,\)冊なので\(\,x=15\,\)を代入して
　\(\begin{eqnarray}
y&=&600\times (15)+18000\\
&=&9000+18000\\
&=&\underline{　27000　円}\\
\end{eqnarray}\)

②
\(\,㋐\,\)
\(\,\mathrm{B}\,\)で総費用\(\,40000\,\)円以内なので
　\(\begin{eqnarray}\displaystyle
600x+18000&≦&40000\\
600x&≦&40000-18000\\
600x&≦&22000\\
x&≦&\frac{220}{6}=36.6\cdots
\end{eqnarray}\)

答え　\(\,\underline{　36　冊}\,\)

冊数は整数なので満たす最大値は\(\,36\,\)になります。

\(\,㋑\,\)
　\(\hspace{4pt}y=1250x\)
のグラフ（原点を通る直線）を書き込むだけです。

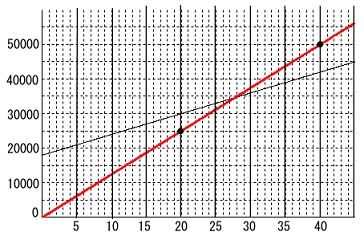
　\(\,(\,20\,,\,25000\,)\,,\,(\,40\,,\,50000\,)\,\)
を通る直線です。

\(\,㋒\,\)
何冊以上で\(\,\mathrm{B}\,\)が安くなるかです。
関数のグラフで\(\,y=600x+18000\,\)が下になることと同じなので
　\(\begin{eqnarray}\displaystyle
600x+18000&\color{blue}{≦}&1250x\\
-650x&\color{blue}{≦}&-18000\\
65x&\color{red}{≧}&1800\\
x&\color{red}{≧}&\frac{1800}{65}=27.69\cdots
\end{eqnarray}\)

これを満たす整数は\(\,28\,\)以上の整数です。

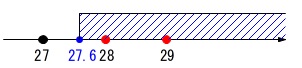
答え　\(\,\underline{　28　冊以上}\,\)

(2)
線分図を書いて進めれば簡単な連立方程式です。
問題に指示がなければ\(\,1\,\)次方程式でも解けますが、
連立方程式を立てて穴埋めをしなくてはなりません。

条件
　家から駅まで\(\,1800\,\)移動する。
　始め毎分\(\,60\,\)で歩く。
　途中から毎分\(\,160\,\)で走る。
　\(\,20\,\)分で駅に到着した。
（道のりの単位は\(\,\mathrm{m}\,\)ですが途中計算では省略します。）

歩いた道のりを\(\,x\,\)、走った道のりを\(\,y\,\)として連立方程式を立てて、
その連立方程式を解きます。
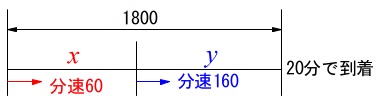1つは道のりの和が\(\,1800\,\)であること。
もう一つは歩いた時間と走った時間の和が\(\,20\,\)分であること。

時間は道のりを速さで割れば出てくるので、
　歩いた時間\(\,\displaystyle \frac{\color{red}{x}}{\color{red}{60}}\,\)
　走った時間\(\,\displaystyle \frac{\color{blue}{y}}{\color{blue}{160}}\,\)

よって、連立方程式は
　\(\begin{cases}
\hspace{4pt} x+y=1800　･･･(ⅰ)\\
\hspace{4pt}\displaystyle \frac{x}{60}+\frac{y}{160}=20　･･･(ⅱ)
\end{cases}\)

答え　\(\,①　\underline{　x+y　}\)　\(②　\displaystyle \underline{　\frac{x}{60}+\frac{y}{160}　}\,\)

連立方程式を解くときは一文字消去ですが、
その前に(ⅱ)の分母を無くしておきましょう。

\(\,(ⅱ)\times 480\,\)から
　\(\hspace{4pt}8x+3y=9600　･･･(ⅱ)’\)

\(\,(ⅰ)(ⅱ)’\,\)から\(\,y\,\)を消去しましょう。

\(\,(ⅱ)’-(ⅰ)\times 3\,\)です。

　\(\hspace{16pt}8x+3y=9600\\
\underline{-\,)\,3x+3y=5400}\\
\hspace{14pt}5x\hspace{20pt}=4200\\
\hspace{40pt}x=840\)

(ⅰ)にもどして
　\(\begin{eqnarray}
840+y&=&1800\\
y&=&1800-840\\
&=&960
\end{eqnarray}\)

答え　\(\,③　\underline{　840　}\,\)　\(\,④　\underline{　960　}\,\)

きれいな数値ですが計算ミスには気をつけましょう。

(3)
大小2つのさいころを投げる確率です。

　大きいさいころの出た目を十の位
　小さいさいころの出た目を一の位
としたときにできる
　\(\,2\,\)けたの数を\(\,m\,\)とする。

2つのさいころなので樹形図でも表でも良いです。

ここでは2つのさいころを投げてでできる、
\(\,2\,\)けたの自然数は\(\,36\,\)通りある、ということで進めます。

①
\(\,m\,\)が素数となる確率です。

各桁の数は\(\,1\,\)から\(\,6\,\)までしかないので、
\(\,11\,\)から\(\,66\,\)までの\(\,2\,\)けたの素数を抜き出すと
　\(\,11,13,23,31,41,43,53,61\,\)
の\(\,8\,\)通りしかありません。

答え　\(\,\displaystyle \frac{8}{36}=\underline{　\frac{2}{9}　}\,\)

樹形図や表の方が抜け落ちなく確実ですよ。

②
\(\,\sqrt{m}\,\)が自然数となる確率です。

\(\,\sqrt{m}\,\)が自然数となるのは、
\(\,m\,\)が平方数（\(\,a^2\,\))になるときです。

\(\,11\,\)から\(\,66\,\)までの自然数で平方数は
　\(\,16,25,36,\color{red}{49},64\,\)
ですが、さいころに\(\,9\,\)はないので\(\,49\,\)は\(\,m\,\)にはなりません。

よって、\(\,36\,\)通りの中に4つ平方数があります。

答え　\(\,\displaystyle \frac{4}{36}=\underline{　\frac{1}{9}　}\,\)

\(\,2\,\)けたの自然数を表にしておくので確認しておいてください。
　赤字が大きいさいころの出た目
　青字が小さいさいころの出た目
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & \color{magenta}{11} & 12 & \color{magenta}{13} & 14 & 15 & \color{green}{16}● \\ \hline
\color{red}{2} & 21 & 22 & \color{magenta}{23} & 24 & \color{green}{25}● & 26 \\ \hline
\color{red}{3} & \color{magenta}{31} & 32 & 33 & 34 & 35 & \color{green}{36}● \\ \hline
\color{red}{4} & \color{magenta}{41} & 42 & \color{magenta}{43} & 44 & 45 & 46 \\ \hline
\color{red}{5} & 51 & 52 & \color{magenta}{53} & 54 & 55 & 56 \\ \hline
\color{red}{6} & \color{magenta}{61} & 62 & 63 & \color{green}{64}● & 65 & 66 \\ \hline
\end{array}\)

第３問関数総合問題

\(\color{black}{\fbox{3}}\)

比例定数の決定から四角形を\(\,2\,\)等分する直線を求める問題までの基本問題です。

条件
　関数\(\,y=ax^2　･･･㋐\,\)
　関数\(\,y=3x+7　･･･㋑\,\)
　\(\,㋐㋑\,\)の交点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-2\,\)

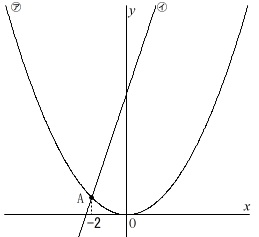
(1)
\(\,a\,\)を求めます。
\(\,a\,\)は関数\(\,y=ax^2\,\)の比例定数です。

点\(\,\mathrm{A}\,\)は関数\(\,y=ax^2\,\)の点ですが、
関数\(\,y=3x+7\,\)上の点でもあるので\(\,x\,\)座標が\(\,-2\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&3(-2)+7\\
&=&1
\end{eqnarray}\)

これから
　\(\,\mathrm{A}\,(\,-2\,,\,1\,)\,\)

これを\(\,y=ax^2\,\)に代入して
　\(\begin{eqnarray}\displaystyle
1&=&a(-2)^2\\
&=&4a\\
a&=&\underline{　\frac{1}{4}　}
\end{eqnarray}\)

(2)
\(\,㋐\,\)\(\displaystyle \,y=\frac{1}{4}\,x^2\,\)で、
\(\,x\,\)の変域が\(\,-2≦x≦3\,\)のときの\(\,y\,\)の変域を求めます。
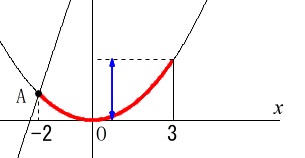最小値は\(\,x=0\,\)のときの\(\,y=0\,\)、
最大値は\(\,x=3\,\)のとき\(\displaystyle \,y=\frac{9}{4}\,\)

よって、
　\(\displaystyle \,\underline{　0\,≦\,y\,≦\,\frac{9}{4}　}\,\)

できるだけグラフをかいて確認した方が良いですが、
\(\,y\,\)軸対称なので\(\,x\,\)の変域から
「\(\,x=-2\,\)のときは最大値、最小値には関係がない」
ということが分かれば良いです。

(3)
条件が加わります。

　\(\,y=3x+7\,\)の\(\,y\,\)切片を\(\,\mathrm{B}\,\)
　\(\displaystyle \,y=\frac{1}{4}x^2\,\)上で\(\,x=6\,\)の点を\(\,\mathrm{C}\,\)
　四角形\(\,\mathrm{ADCB}\,\)が平行四辺形になる点を\(\,\mathrm{D}\,\)

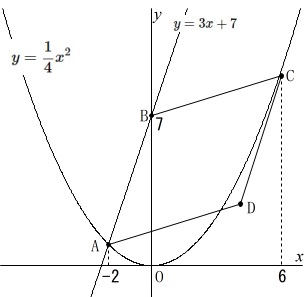
①
点\(\,\mathrm{D}\,\)の座標を求めます。

\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,0\,\)なので
　\(\,\mathrm{B}\,(\,0\,,\,7\,)\,\)

\(\,\mathrm{C}\,\)は\(\displaystyle \,y=\frac{1}{4}x^2\,\)上の点で
\(\,x\,\)座標が\(\,6\,\)なので
　\(\,\mathrm{C}\,(\,6\,,\,9\,)\,\)

\(\,2\,\)点\(\,\mathrm{B,C}\,\)をみると
　\(\,x\,\)座標が\(\,+6\,\)、\(\,y\,\)座標が\(\,+2\,\)増加
しています。

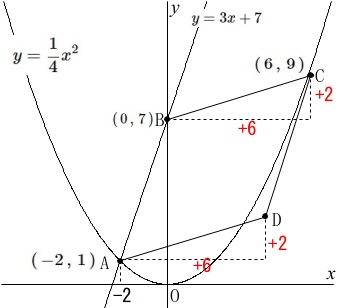
四角形\(\,\mathrm{ADCB}\,\)が平行四辺形なので
\(\,2\,\)点\(\,\mathrm{A,D}\,\)も同じ増加をしています。

\(\,\mathrm{A}\,\)の座標が\(\,(\,-2\,,\,1\,)\,\)だから
　\(\,\mathrm{D}\,\underline{　(\,4\,,\,3\,)　}\,\)

平行四辺形なので\(\,2\,\)点\(\,\mathrm{A,B}\,\)の変化を\(\,\mathrm{D,C}\,\)もしている、でも良いです。

②
点\(\,\mathrm{O}\,\)（原点）を通り、
平行四辺形\(\,\mathrm{ADCB}\,\)の面積を\(\,2\,\)等分する直線の式を求めます。

平行四辺形は対角線の交点を通る直線で面積が\(\,2\,\)等分されます。
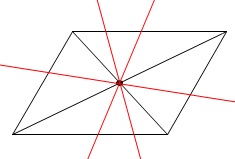このことから
　原点と\(\,\mathrm{A,C}\,\)の中点
または
　原点と\(\,\mathrm{B,D}\,\)の中点
を通る直線が平行四辺形\(\,\mathrm{ADCB}\,\)を\(\,2\,\)等分します。

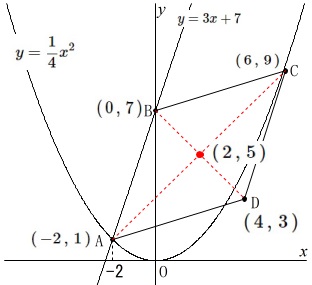
\(\,\mathrm{A,C}\,\)の中点と\(\,\mathrm{B,D}\,\)の中点は同じで
　\((\,2\,,\,5\,)\)
だから求める原点\(\,\mathrm{O}\,\)を通る直線は
　\(\hspace{10pt}\displaystyle　\underline{　y= \frac{5}{2}\,x　}\)

第４問立体図形問題と作図

\(\color{black}{\fbox{4}}\)
正四面体の内部の辺の長さを求めます。

条件
　立体\(\,\mathrm{ABCD}\,\)は正四面体
　\(\,\mathrm{AB}\,\)を\(\,1:2\,\)に分ける点を\(\,\mathrm{E}\,\)
　\(\,\mathrm{DC}\,\)の中点を\(\,\mathrm{F}\,\)
　\(\,\mathrm{AB=6}\,\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）

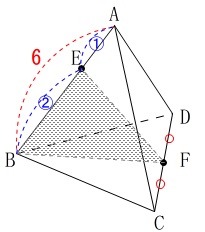
①
辺\(\,\mathrm{BF}\,\)の長さを求めます。

辺\(\,\mathrm{BF}\,\)は底面の正三角形\(\,\mathrm{BCD}\,\)の中線です。
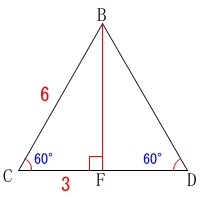\(\,\mathrm{△BCF}\,\)は三角定規なので
　\(\,\mathrm{CF:BF=1:\sqrt{3}}\,\)
よって
　\(\,\mathrm{BF}=\underline{　3\sqrt{3}　\mathrm{cm}}\,\)

②
辺\(\,\mathrm{BF}\,\)を底辺としたときの\(\,\mathrm{△AEF}\,\)の高さを求めます。

\(\,\mathrm{△ABF}\,\)は\(\,\mathrm{△BCD}\,\)に垂直な面なので、
\(\,\mathrm{A,E}\,\)から\(\,\mathrm{△BCD}\,\)に下ろした垂線は辺\(\,\mathrm{BF}\,\)上におります。
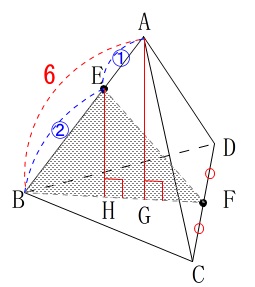このことから求める高は\(\,\mathrm{EH}\,\)となります。

\(\,\mathrm{A}\,\)から\(\,\mathrm{△BCD}\,\)に下ろした垂線は\(\,\mathrm{△BCD}\,\)の重心に下りるので、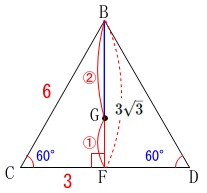　\(\begin{eqnarray}\displaystyle
\mathrm{BG}&=&\frac{2}{3}\times 3\sqrt{3}\\
&=&2\sqrt{3}
\end{eqnarray}\)

\(\,\mathrm{△ABG}\,\)は直角三角形で、
　\(\begin{eqnarray}\displaystyle
\mathrm{AG^2+BG^2}&=&\mathrm{AB^2}\\
\mathrm{AG^2}+(2\sqrt{3})^2&=&6^2\\
\mathrm{AG^2}&=&36-12\\
&=&24\\
\mathrm{AG}&=&\pm 2\sqrt{6}
\end{eqnarray}\)
長さだから\(\,\mathrm{AG}\,＞\,0\,\)なので
　\(\mathrm{AG}=2\sqrt{6}\)
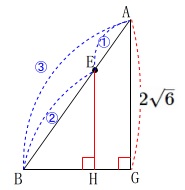\(\,\mathrm{△AGB}\,\)∽\(\,\mathrm{△EHB}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AG:EH}&=&\mathrm{AB:EB}\\
2\sqrt{6}:\mathrm{EH}&=&3:2\\
3\times \mathrm{EH}&=&2\times 2\sqrt{6}\\
\mathrm{EH}&=&\underline{　\frac{4\sqrt{6}}{3}　\mathrm{cm}}
\end{eqnarray}\)

正四面体では高さがどこになるかは覚えておくと良いです。

(2)
円と接点の作図です。

中心が四角形\(\,\mathrm{ABCD}\,\)の辺\(\,\mathrm{AB}\,\)上にあり、
辺\(\,\mathrm{BC}\,\)と辺\(\,\mathrm{AD}\,\)に接する円と辺\(\,\mathrm{BC}\,\)の接点\(\,\mathrm{P}\,\)を作図します。

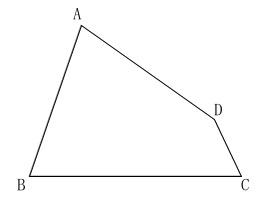
この問題は作図するのは円と接点の両方なのか、
接点\(\,\mathrm{P}\,\)のみなのかで悩むところです。

でも、「接点\(\,\mathrm{P}\,\)を作図しなさい。」の方が自然かな。

手順によっては接点\(\,\mathrm{P}\,\)が先に出てきますが、
円を書いても減点対象にはならないでしょう。

角の二等分線は\(\,2\,\)辺から等しい距離にある点の集まりなので、
三角形の2つの辺に接する円の中心は、
\(\,2\,\)辺の角の二等分線上にあります。
ここでは三角形の\(\,2\,\)辺が見えていないので、
\(\,\mathrm{AD,BC}\,\)を延長して三角形にしてしまいましょう。
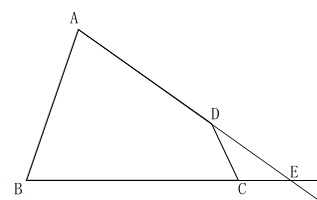直線\(\,\mathrm{AD,BC}\,\)の交点を\(\,\mathrm{E}\,\)として、
\(\,\mathrm{∠AEC}\,\)の二等分線をかいて、
\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{O}\,\)すると、
\(\,\mathrm{BC,AD}\,\)の接する円の中心となります。
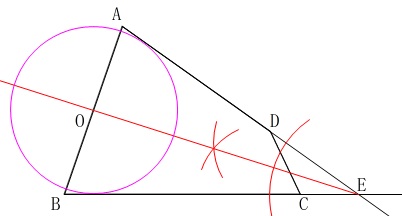ただし、この円の半径は\(\,\mathrm{BC}\,\)と\(\,\mathrm{AD}\,\)に接しているかのようにかいただけなので不確かですよね。

半径をしっかり決めるために、
\(\,\mathrm{O}\,\)から\(\,\mathrm{BC}\,\)に垂線を引けば接点\(\,\mathrm{P}\,\)が見つかります。
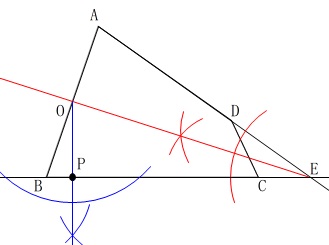\(\,\mathrm{AD}\,\)に垂線を引いても半径は決まりますが、
\(\,\mathrm{BC}\,\)側に垂線を引けば先に\(\,\mathrm{P}\,\)が見つかることに気がつきます。

円に接する接線は接点において半径と垂直になるので、
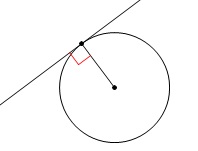そのことから逆に垂線を引く手順は必ず入ると考えておくのも良いですね。

第５問平面図形総合問題

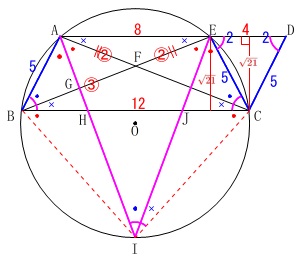
\(\color{black}{\fbox{5}}\)

円と平行四辺形を組合わせた平面図形総合問題です。

条件
　\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{AI}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線
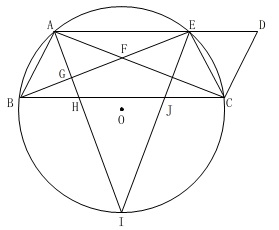対称性があるのでいろいろなことが分かりますが、
問題の順に進めます。

(1)
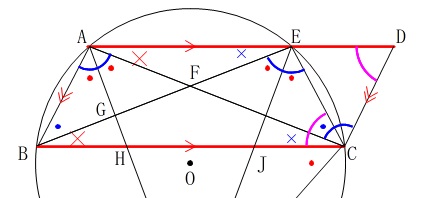
\(\,\mathrm{△AHC}\,\)∽\(\,\mathrm{△CJI}\,\)を証明します。
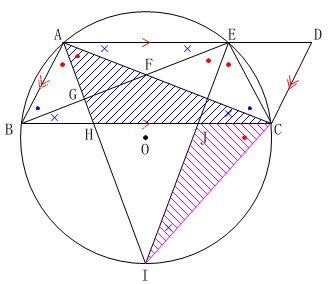円周角と平行線の性質から、
分かることを図に書き込めば証明は終わっています。

（証明）\(\,\mathrm{△AHC}\,\)∽\(\,\mathrm{△CJI}\,\)において
線分\(\,\mathrm{AI}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線だから
　\(\mathrm{∠HAC}=\color{black}{\fbox{\(\,\mathrm{∠BAH}\,\)}}　･･･①\)
弧\(\,\mathrm{BI}\,\)に対する円周角は等しいから
　\(\color{black}{\fbox{\(\,\mathrm{∠BAH}\,\)}}=\mathrm{∠JCI}　･･･②\)
①②から
　\(\mathrm{∠HAC}=\mathrm{∠JCI}　･･･③\)
仮定から\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)で錯角が等しくなるから
　\(\mathrm{∠ACH}=\color{black}{\fbox{\(\,\mathrm{∠CAE}\,\)}}　･･･④\)
また、弧CEに対する円周角は等しいから
　\(\color{black}{\fbox{\(\,\mathrm{∠CAE}\,\)}}=\mathrm{∠CIJ}　･･･⑤\)
④⑤から
　\(\mathrm{∠ACH}=\mathrm{∠CIJ}　･･･⑥\)
③⑥から
　\(\color{black}{\fbox{　２組の角　}}\,\) がそれぞれ等しい。
よって、
　\(\,\mathrm{△AHC}\,\)∽\(\,\mathrm{△CJI}\,\)

答え
　（ア）\(\,\mathrm{\underline{　∠BAH　}}\,\)
　（イ）\(\,\underline{　\mathrm{∠CAE}　}\,\)
　（ウ）\(\,\underline{　２組の角　}\,\)

（ア）（イ）においては角の大きさが等しいことが言えれば良いので、
記号の順番は気にしなくて構いません。
ただし、\(\,\mathrm{∠HAC=∠JCI}\,\)などは相似な三角形の角なので順番をそろえます。

(2)
\(\,\mathrm{△ADC}\,\)≡\(\,\mathrm{△BCE}\,\)であることを証明します。
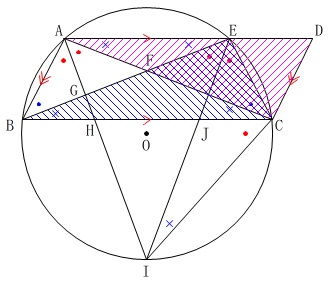利用する定理をかえるといくつか証明方法があります。

(1)で示した図形で\(\,\color{blue}{×}\,\)は、
平行線の錯角と円周角の定理を利用して等しいことを示しています。

\(\,\mathrm{△FAE}\,\)と\(\,\mathrm{△FBC}\,\)は二等辺三角形なので、
　\(\mathrm{\color{red}{FA}=\color{red}{FE}\,,\,\color{blue}{FB}=\color{blue}{FC}}\)
から
　\(\hspace{4pt}\mathrm{AC=BE}\)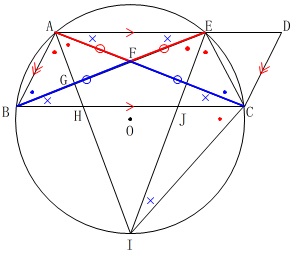平行四辺形の対辺から
　\(\hspace{4pt}\mathrm{AD=BC}\)
さらに、同じ弧の円周角なので
　\(\hspace{4pt}\mathrm{∠DAC=∠CBE}\)
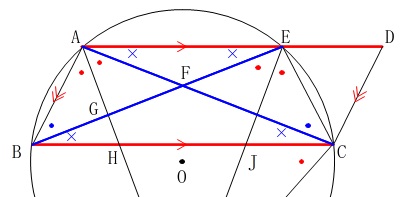これらのことから\(\,2\,\)組の辺とその間の角がそれぞれ等しいことが言えます。

または、\(\,\mathrm{AC}\,\)は平行四辺形の対角線なので
　\(\,\mathrm{△ADC}\,\)≡\(\,\mathrm{△CBA}\,\)
だから
　\(\,\mathrm{△CBA}\,\)≡\(\,\mathrm{△BCE}\,\)
であることをいえば証明になります。

円を平行線で切っているので、
四角形\(\,\mathrm{ABCE}\,\)が等脚台形になるので、
平行四辺形の対辺が等しいことをいえばさらに条件は増えます。

合同条件さえ言えれば経路は違って構いませんが、
ここでは普通に証明しておきます。

（証明）\(\,\mathrm{△ADC}\,\)と\(\,\mathrm{△BCE}\,\)において
平行四辺形の対辺であることから
　\(\hspace{4pt}\mathrm{AD=BC}　･･･①\)
弧\(\,\mathrm{CE}\,\)に対する円周角は等しいので
　\(\hspace{4pt}\mathrm{∠CAD=∠EBC}　･･･②\)
\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)なので錯角が等しく
　\(\mathrm{\color{red}{∠BAC}=\color{blue}{∠ACD}}　･･･③\)
また、弧\(\,\mathrm{BC}\,\)の円周角は等しいので
　\(\mathrm{\color{red}{∠BAC}=\color{blue}{∠BEC}}　･･･④\)
③④より
　\(\mathrm{\color{blue}{∠ACD}=\color{blue}{∠BEC}}　･･･⑤\)
②⑤から三角形の\(\,2\,\)角が等しいので残りの1つも等しく
　\(\hspace{4pt}\mathrm{∠ADC=∠BCE}　･･･⑥\)
①②⑥から
　\(\,1\,\)組の辺とその両端角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ADC}\,\)≡\(\,\mathrm{△BCE}\,\)
実際に証明するときは証明を書き出す前に図の中で確認しておきましょう。

(3)
面積と線分比を求めます。

長さの条件が加わります。
　\(\,\mathrm{AB=5}\,\)
　\(\,\mathrm{AE=8}\,\)
　\(\,\mathrm{BC=12}\,\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
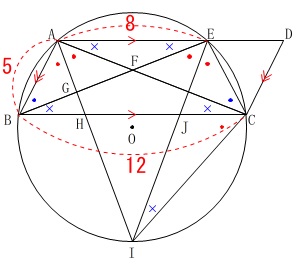ようやく具体性が出てきたのですが、
ここまででほとんどの情報は出てきています。

①
平行四辺形\(\,\mathrm{ABCD}\,\)の面積を求めます。
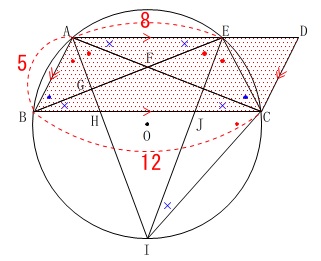底辺は\(\,\mathrm{BC=12}\,\)で、
\(\,\mathrm{AD}\,\)と\(\,\mathrm{BC}\,\)との距離が高さになります。

四角形\(\,\mathrm{ABCE}\,\)は等脚台形なので、
\(\,\mathrm{A\,,\,E}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろします。
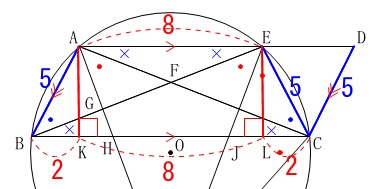\(\,\mathrm{△ABK}\,\)と\(\,\mathrm{△ECL}\,\)は合同な直角三角形で、
　\(\begin{eqnarray}\displaystyle
\mathrm{AK^2+BK^2}&=&\mathrm{AB^2}\\
\mathrm{AK^2}+2^2&=&5^2\\
\mathrm{AK^2}&=&21\\
\mathrm{AK}&=&\pm \sqrt{21}
\end{eqnarray}\)

長さだから\(\,\mathrm{AK\,＞\,0}\,\)なので
　\(AK=\sqrt{21}\)

これが平行四辺形\(\,\mathrm{ABCD}\,\)の高さなので面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{BC}\times \mathrm{AK}\\
&=&12\times \sqrt{21}\\
&=&\underline{　12\sqrt{21}　\mathrm{cm^2}}
\end{eqnarray}\)

②
線分\(\,\mathrm{BG}\,\)と線分\(\,\mathrm{FE}\,\)の長さの比を求めます。
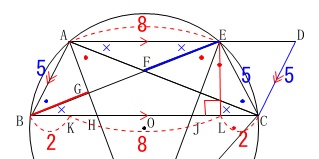相似を使うことになるので比でも良いのですが、
\(\,\mathrm{BE}\,\)の長さが具体的に出るので実際の長さを使うことにします。

\(\,\mathrm{△BEL}\,\)は直角三角形なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{BE}&=&\sqrt{10^2+(\sqrt{21})^2}\\
&=&\sqrt{100+21}\\
&=&\sqrt{121}\\
&=&11
\end{eqnarray}\)

トレミーの定理でもすぐに出ますが、
三平方の定理で十分です。

また、\(\,\mathrm{△AFE}\,\)∽\(\,\mathrm{△CFB}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{EF:BF}&=&\mathrm{AE:CB}\\
\mathrm{EF:BF}&=&\color{red}{8}:\color{red}{12}\\
&=&2:3
\end{eqnarray}\)

これから
　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\frac{2}{2+3}\times 11\\
&=&\color{blue}{\frac{22}{5}}
\end{eqnarray}\)

このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&11-\frac{22}{5}\\
&=&\frac{55-22}{5}\\
&=&\frac{33}{5}
\end{eqnarray}\)

\(\,\mathrm{△FAE}\,\)は二等辺三角形なので
　\(\displaystyle \mathrm{EF=AF}=\color{blue}{\frac{22}{5}}\)
であることも確認しておきましょう。
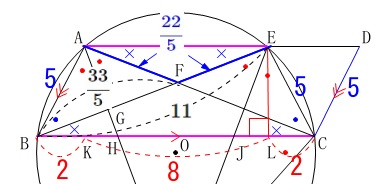後は\(\,\mathrm{BG}\,\)の長さを求めれば終わりです。

見にくいので\(\,\mathrm{△ABE}\,\)を抜き出します。
線分\(\,\mathrm{BG}\,\)で線分比を利用したいので、
\(\,\mathrm{BG:GF}\,\)が知りたいところです。

三重県では角の二等分線定理を中学校で教えているのでしょう。
毎年のように使いますね。
それとも試験中に自分で考えて定理を導きながら解くことを求めているのでしょうか。
補助線は平行線1つで済むとはいえ、解答時間に差がつきます。

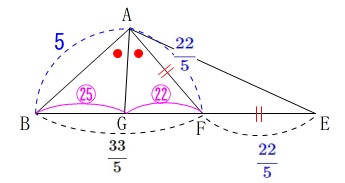
角の二等分線定理（※）から
　\(\begin{eqnarray}\displaystyle
\mathrm{BG:GF}&=&\mathrm{AB:AF}\\
&=&5:\frac{22}{5}\\
&=&25:22
\end{eqnarray}\)
これから
　\(\begin{eqnarray}\displaystyle
\mathrm{BG}&=&\frac{25}{25+22}\times \frac{33}{5}\\
&=&\frac{25}{47}\times \frac{33}{5}\\
&=&\color{red}{\frac{5\times 33}{47}}
\end{eqnarray}\)

角の二等分線定理を知らない、という場合でも平行線1つで解決します。
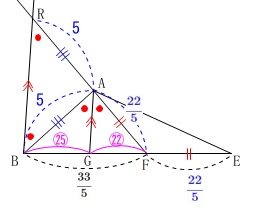\(\,\mathrm{B}\,\)を通り\(\,\mathrm{AG}\,\)に平行な線を引き、
\(\,\mathrm{FA}\,\)の延長との交点を\(\,\mathrm{R}\,\)とすると、
平行線の錯角と同位角が等しくなるので\(\,\mathrm{△ABR}\,\)が二等辺三角形になります。
　\(\,\mathrm{AB=AR}\,\)

このとき、
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AF}&=&\mathrm{AR:AF}\\
&=&5:\frac{22}{5}\\
&=&25:22
\end{eqnarray}\)
となります。

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{BG:FE}&=&\color{red}{\frac{5\times 33}{47}}:\color{blue}{\frac{22}{5}}\\
&=&\frac{5\times 3}{47}:\frac{2}{5}\\
&=&\underline{　75:94　}
\end{eqnarray}\)

※
\(\color{red}{\fbox{　内角の二等分線定理　}}\)
　\(\,\mathrm{△ABC}\,\)において\(\,\mathrm{∠BAC}\,\)の（内角の）二等分線と、
　\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{D}\,\)とするとき、
　\(\,\mathrm{AB:AC=BD:DC}\,\)
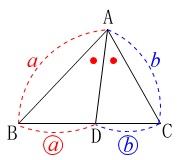証明は上で使った方法と同じ平行線です。