滋賀県公立高校入試2020年(令和２年)度の数学の問題と解説

２０２０年(令和２年)度に滋賀県で実施された公立高校入試の数学の問題と解説です。
具体的、機械的に処理できる問題と一般的な応用が必要な問題とのバランスの取れた大問で４問があります。
滋賀の県立入試は隠れた難関なので数学は高得点を取っておきたい科目です。

滋賀県公立高校入試2020年(令和２年)度の数学の問題と解説

\(\color{black}{\fbox{1}}\)の計算が主な小問集合から、
\(\color{black}{\fbox{4}}\)の図形を等分する作図応用問題があります。

おおよそ中学数学全般からの出題で偏った出題はありません。

滋賀県公立高校入試2020年(令和２年)度の数学の問題

問題は滋賀県が公開してくれているものから解答用紙を除いています。
解答用紙を確認したい人は滋賀県の公式ページからご確認ください。

⇒　令和2年度滋賀県公立高校入試数学の問題

記述問題が少しありますが、
日本語の力を問うようなまとめにくい問題ではく、
普通に答えを導く過程をまとめれば良いようにしてくれています。

滋賀県公立高校入試2020年(令和２年)度の数学の解説

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{4}}\)までの解説を一気にまとめます。

第１問

\(\large{\color{black}{\fbox{1}}}\)

数と式から方程式、確率などの計算問題小問集合\(\,9\,\)問です。

(1)
　\(\,3\,\)月は\(\,-11\,\)、\(\,4\,\)月は\(\,+6\,\)
なので\(\,2\,\)か月間では
　\(\hspace{10pt}-11+6\\
=\underline{　-5　人}\)

基準値がないので自分で基準をおいて数直線で見れば明らかです。
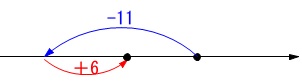正の数負の数を数直線で見る基本ですね。

(2)
　\(\hspace{10pt}\displaystyle \frac{7}{4}\,a-\frac{3}{5}\,a\\
\displaystyle =\frac{35\,a-12\,a}{20}\\
\displaystyle =\underline{　\frac{23\,a}{20}　}\)

分母は通分して1つにして、
分子の計算に集中します。

答えは\(\,\displaystyle \underline{　\frac{23}{20}\,a　}\,\)でも同じです。
\(\,a\,\)は分子にあります。

(3)
連立方程式は一文字消去です。
　\(\begin{cases}
\hspace{4pt} 2x-3y=1　･･･①\\
\hspace{4pt} 3x+2y=8　･･･②
\end{cases}\)

どちらからでもいいですが\(\,y\,\)を消去します。

\(\,①\times 2+②\times 3\,\)です。
　\(\hspace{14pt}4x-6y=2\\
\underline{+\,)\,9x+6y=24}\\
\hspace{10pt}13x\hspace{22pt}=26\\
\hspace{42pt}x=2\)

\(\,①②\,\)のどちらかに代入して\(\,y\,\)を求めます。
ここでは\(\,②\,\)に代入します。

　\(\begin{eqnarray}
3(2)+2y&=&8\\
6+2y&=&8\\
2y&=&2\\
y&=&1
\end{eqnarray}\)

答え　\(\,\underline{　x=2\,,\,y=1　}\,\)

(4)
　\(\hspace{10pt}\sqrt{3}(2-\sqrt{6})\\
=2\sqrt{3}-\sqrt{18}\\
=\underline{　2\sqrt{3}-3\sqrt{2}　}\)

ルートの中が違うのでこれ以上計算できません。
素因数分解は確実にやっておきましょう。

無理数計算に慣れている人は
　\(\hspace{10pt}\sqrt{3}(2-\sqrt{6})\\
=2\sqrt{3}-3\sqrt{2}\)
で構いません。

(5)
\(\,2\,\)次方程式は因数分解から試して見ると良いです。
　\(\begin{eqnarray}
x^2-7x+12&=&0\\
(x-3)(x-4)&=&0\\
x&=&\underline{　3\,,\,4　}
\end{eqnarray}\)

因数分解できないときは解の公式になります。

(6)
　\(\hspace{10pt}x^3\times (6xy)^2\div (-3x^2y)\\
\displaystyle =-\frac{x^3\times 36x^2y^2}{3x^2y}\\
=\underline{　-12x^3y　}\)

割り算は逆数の掛け算なので\(\,\div\,\)の直後は分母になります。
全体の符号に注意ですね。

(7)
領域問題は簡単なグラフをかいて確認すると良いです。
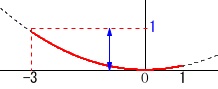\(\,y\,\)の変域\(\,y=0\,\)は原点、
最大値\(\,y=1\,\)は軸から遠い\(\,x=-3\,\)のときの値です。

\(\,y=ax^2\,\)に代入して
　\(\begin{eqnarray}\displaystyle
1&=&a\times (-3)^2\\
&=&9a\\
a&=&\underline{　\frac{1}{9}　}
\end{eqnarray}\)

放物線は軸に対して対称です。

(8)
\(\,100\,\)人でも\(\,1000\,\)人でも最も度数の多い値が最頻値です。

答え　\(\,\underline{　7　点}\,\)

(9)
等積移動と確率の融合問題です。
カードの取り出し方は\(\,4\,\)枚から\(\,2\,\)枚取り出すので\(\,6\,\)通り。
　\((\,\mathrm{C,D}\,)\,,\,(\,\mathrm{C,E}\,)\,,\,(\,\mathrm{C,F}\,)\)
　\((\,\mathrm{D,E}\,)\,,\,(\,\mathrm{D,F}\,)\,,\,(\,\mathrm{E,F}\,)\)
書き出せばすぐに分かります。

この\(\,2\,\)点と\(\,\mathrm{A}\,\)とでできる三角形の面積が、
\(\,\mathrm{△DFC}\,\)と等しくなる確率を求めます。

四角形\(\,\mathrm{ABCD}\,\)は平行四辺形で、
\(\,\mathrm{AC}\,\)∥\(\,\mathrm{EF}\,\)なので、
\(\,\mathrm{△DFC}\,\)と面積が等しい三角形は
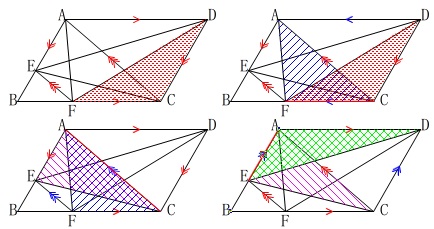底辺を共通に持ち、頂点が平行移動する三角形を次々に探していくと、
　\(\mathrm{\color{red}{△DFC}=\color{blue}{△ACF}=\color{magenta}{△ACE}=\color{green}{△ADE}}\)

カード\(\,6\,\)通りの取り出し方に対し、
面積が等しくなるのは\(\,3\,\)通り。
　\((\,\mathrm{C,D}\,)\,,\,\color{red}{(\,\mathrm{C,E}\,)}\,,\,\color{red}{(\,\mathrm{C,F}\,)}\)
　\(\color{red}{(\,\mathrm{D,E}\,)}\,,\,(\,\mathrm{D,F}\,)\,,\,(\,\mathrm{E,F}\,)\)

よって、求める確率は
　\(\hspace{4pt}\displaystyle \frac{3}{6}=\underline{　\frac{1}{2}　}\)

第２問

\(\large{\color{black}{\fbox{2}}}\)

\(\,1\,\)次関数と方程式の問題です。

観光バスツアーでも何でも良いのですが、
　参加費：一人\(\,5000\,\)円
　定員：\(\,45\,\)人
　固定費用：\(\,80000\,\)円
　別途費用：一人\(\,1900\,\)円

金額\(\,y\,\)、人数\(\,x\,\)とすると
売り上げ
　\(\hspace{4pt}y=5000\,x　･･･①\)
費用
　参加者費用
　\(\hspace{4pt}y=1900\,x　･･･②\)
　ツアー総費用
　\(\hspace{4pt}y=1900\,x+80000　･･･③\)
利益
　\(\hspace{10pt}5000\,x-(1900\,x+80000)\\
=3100\,x-80000　･･･④\)

これらは「調べたこと」に書いてあります。

(1)
参加者が\(\,15\,\)人とき売り上げは\(\,①\,\)から
　\(\begin{eqnarray}\displaystyle
y&=&5000\times (15)\\
&=&\underline{　75000　円}
\end{eqnarray}\)

(2)
利益をプラスにするためには何人の参加が必要かを求めます。
\(\,④\,\)から
　\(\begin{eqnarray}\displaystyle
3100\,x-80000&＞&0\\
3100\,x&＞&80000\\
x&＞&\frac{80000}{3100}=25.8\cdots
\end{eqnarray}\)
なので\(\,26\,\)人以上参加しないと利益はプラスになりません。
（\(\,25\,\)人ではマイナスです。）

答え　\(\,\underline{　26　人}\,\)

(3)
グラフの読み取りです。
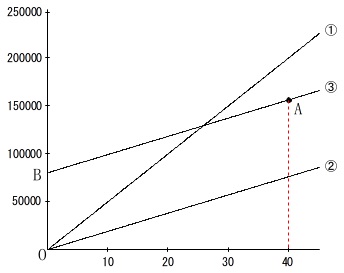\(\,x=40\,\)のときの点\(\,\mathrm{A}\,\)の\(\,y\,\)座標と、
\(\,x=0\,\)のときの点\(\,\mathrm{B}\,\)の\(\,y\,\)座標の差は何を表しているかを選びます。

\(\,\mathrm{A}\,\)の\(\,y\,\)座標は\(\,40\,\)人参加したときの総費用、
\(\,\mathrm{B}\,\)の\(\,y\,\)座標は固定費\(\,80000\,\)円なので、
\(\,40\,\)人分の別途費用になります。

関数で見ると\(\,②③\,\)は平行なので、
\(\,\mathrm{A,B}\,\)の\(\,y\,\)座標の差は
\(\,②\,\)の\(\,x=40\,\)のときの\(\,y\,\)座標を意味します。

答え　\(\,\underline{　エ　}\,\)

(4)
\(\,45\,\)人参加したときの利益を\(\,100000\,\)円以上にするため、
参加費をいくらにする必要があるかを求めます。

\(\,45\,\)人のときなので費用は決まります。
　\(\hspace{10pt}1900\times 45+80000\\
=165500　円\)

一人当たりの参加費を\(\,a\,\)とすると、
売り上げは\(\,45\,a\,\)円なので、
利益を\(\,100000\,\)円以上にするためには
　\(\begin{eqnarray}\displaystyle
45\,a-165500&≧&100000\\
45\,a&≧&265500\\
a&≧&5900
\end{eqnarray}\)

答え　\(\,\underline{　5900　円以上}\,\)

\(\,④\,\)の関係式は
　\((売り上げ)-(総費用)=(利益)\)
を意味しています。

第３問

\(\large{\color{black}{\fbox{3}}}\)

平年図形の相似問題です。

見術館の室内とパネルがあって、
見えない部分がある。

と、考えると難しくなります。
問題が示してくれているように、
慣れている平面図形で処理しましょう。

考え方を図にすると図\(\,2\,\)のようになります。
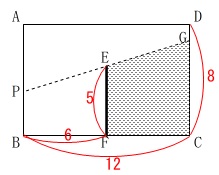\(\,\mathrm{P}\,\)から見えない部分が塗られている部分です。
（単位は\(\,\mathrm{m}\,\)ですが計算途中では省略します。）

見えるということは光が直進して視界に入るので、
見えない部分も直線で切れば良いということです。

(1)
点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)の位置にあるときの線分\(\,\mathrm{CG}\,\)の長さ、
および点\(\,\mathrm{G}\,\)が\(\,\mathrm{D}\,\)に重なったときの線分\(\,\mathrm{AP}\,\)の長さを求めます。

先ず点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)にあるとき
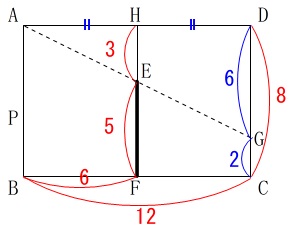\(\,\mathrm{FE}\,\)の延長と\(\,\mathrm{AD}\,\)の交点を\(\,\mathrm{H}\,\)とすると、
　\(\,\mathrm{△AEH}\,\)∽\(\,\mathrm{△AGD}\,\)
で\(\,\mathrm{BF=FC=AH=HD=\color{red}{6}}\,\)なので
　相似比は\(\,1:2\,\)
これから
　\(\begin{eqnarray}
\mathrm{EH:DG}&=&1:2\\
3:\mathrm{DG}&=&1:2\\
\mathrm{DG}&=&\color{blue}{6}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}
\mathrm{CG}&=&\mathrm{DC-DG}\\
&=&\color{red}{8}-\color{blue}{6}\\
&=&\underline{　2　\mathrm{m}}
\end{eqnarray}\)

また、点\(\,\mathrm{G}\,\)が\(\,\mathrm{D}\,\)に重なったときは、
\(\,\mathrm{AP}\,\)は先ほどの\(\,\mathrm{DG}\,\)に等しくなるので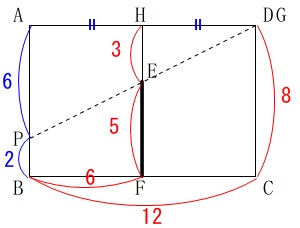
　\(\hspace{4pt}\mathrm{AP}=\underline{　6　\mathrm{m}}\)

(2)
点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)から\(\,\mathrm{C}\,\)側に\(\,\mathrm{2}\,\)移動したとき、

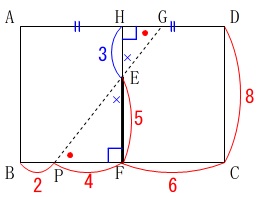
　\(\,\mathrm{△PFE}\,\)∽\(\,\mathrm{△GHE}\,\)
を証明し、線分\(\,\mathrm{DG}\,\)の長さを求めます。

相似は明らかでしょう。

四角形\(\,\mathrm{ABCD}\,\)は長方形だから、
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
平行線の錯角は等しいから
　\(\,\mathrm{∠FPE}\,\)=\(\,\mathrm{∠HGE}\,\)
　\(\,\mathrm{∠PFE}\,\)=\(\,\mathrm{∠GHE}\,\)
また対頂角が等しいことから
　\(\,\mathrm{∠PEF}\,\)=\(\,\mathrm{∠GEH}\,\)
も言えるので「\(\,2\,\)組の角がそれぞれ等しい」ことがすぐに言えます。

証明は自分で好きなようにまとめてください。

　\(\,\mathrm{△PFE}\,\)∽\(\,\mathrm{△GHE}\,\)
が言えたとして、\(\,\mathrm{DG}\,\)の長さを求めます。
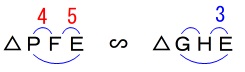　\(\begin{eqnarray}\displaystyle
\mathrm{PF:GH}&=&\mathrm{FE:HE}\\
\color{red}{4}:\mathrm{GH}&=&\color{red}{5}:\color{blue}{3}\\
5\times \mathrm{GH}&=&12\\
\mathrm{GH}&=&\frac{12}{5}
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{GD}&=&\mathrm{HD-HG}\\
&=&\color{red}{6}-\frac{12}{5}\\
&=&\underline{　\frac{18}{5}　\mathrm{m}}
\end{eqnarray}\)

(3)
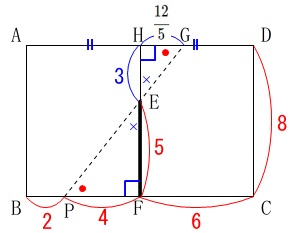
点\(\,\mathrm{P}\,\)が\(\,\mathrm{ＣＤ}\,\)上にあって、
\(\,\mathrm{CP=AG}\,\)となるときの線分\(\,\mathrm{CP}\,\)の長さを求めます。
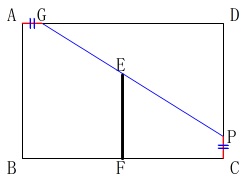長さが与えられているので書き込んでおきましょう。

求める\(\,\mathrm{CP=AG}=x\,\)とすると
　\(\,\mathrm{PD}=8-x\,\)
　\(\,\mathrm{GD}=12-x\,\)
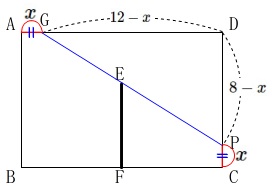このままでは何かが足りていません。
\(\,\mathrm{EF}\,\)を利用していないので条件が足りないのです。

補助線を引きますが平行線か垂線が普通です。
\(\,\mathrm{P,G}\,\)を通る\(\,\mathrm{AD}\,\)と\(\,\mathrm{AB}\,\)に平行な線を引いてみます。
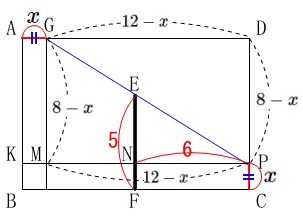それぞれの交点を\(\,\mathrm{K,M,N}\,\)とおいています。

\(\,\mathrm{EF}=5\,\)なので
　\(\,\mathrm{EN}=5-x\,\)（\(\,0\,＜\,x\,＜\,5\,\)）
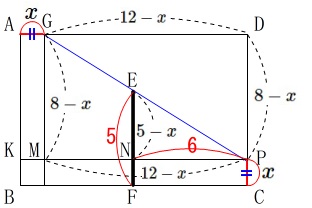ここまで来れば面積でも出そうですが、
相似を利用します。

　\(\,\mathrm{△PEN}\,\)∽\(\,\mathrm{△PGM}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{PN:PM}&=&\mathrm{EN:GM}\\
6:(12-x)&=&(5-x):(8-x)\\
(12-x)(5-x)&=&6(8-x)\\
x^2-17x+60&=&48-6x\\
x^2-11x+12&=&0
\end{eqnarray}\)

因数分解できないので解の公式です。
（ここできましたか。）

　\(\begin{eqnarray}\displaystyle
x&=&\frac{11\pm \sqrt{11^2-4\cdot (1)\cdot (12)}}{2}\\
&=&\frac{11\pm \sqrt{121-48}}{2}\\
&=&\frac{11\pm \sqrt{73}}{2}
\end{eqnarray}\)

ここで
　\(\,8\,＜\,\sqrt{73}\,＜\,9\,\)
だから\(\,0\,＜\,x\,＜\,5\,\)を満たすのは
　\(\displaystyle x=\frac{11-\sqrt{73}}{2}\)

よって、
　\(\displaystyle \,\mathrm{CP}=\underline{　\frac{11-\sqrt{73}}{2}　\mathrm{m}}\,\)

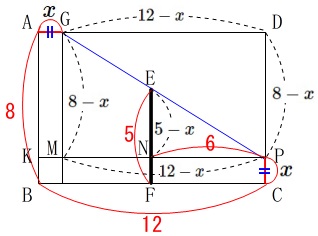\(\,\mathrm{△PEN}\,\)と台形\(\,\mathrm{EGMN}\,\)を加えると、
\(\,\mathrm{△GPD}\,\)と等しくなるなどの面積からも求めることはできます。

いずれにしても解の公式にたどり着きますので確認しておくと良いでしょう。

ところで、
見えない影の部分はどこに行った？

第４問

\(\large{\color{black}{\fbox{4}}}\)

円、三角形、四角形を等しく分けます。

(1)
円を\(\,3\,\)等分する方法です。

円は中心角を\(\,120^{\circ}\,\)にすれば\(\,3\,\)等分することができるので、
\(\,120^{\circ}\,\)の作図と同じです。
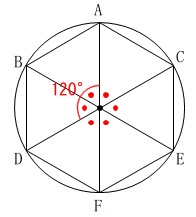円に内接する正六角形を作図するのと同じ、
つまり正三角形を6つ作ればいいわけです。
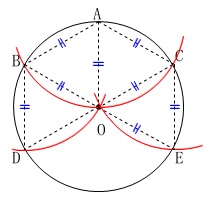半径\(\,\mathrm{OA}\,\)と等しく\(\,\mathrm{AB}\,\)をとると\(\,\mathrm{△ABO}\,\)は正三角形で、
同様に\(\,\mathrm{△ACO}\,\)も正三角形となります。
さらに半径と等しく\(\,\mathrm{BD,CE}\,\)をとると、
\(\,\mathrm{△BDO}\,\)および\(\,\mathrm{△CEO}\,\)も正三角形になるので、
　\(\,\mathrm{∠AOD=∠AOE=120^{\circ}}\,\)
よって、円を\(\,3等\,\)分します。

作図できる角度は多くはありません。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

(2)
正方形の面積を三等分します。

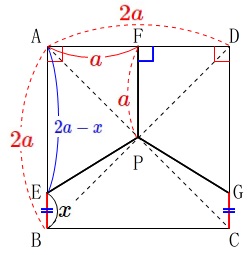
図において、
　四角形\(\,\mathrm{ABCD}\,\)は正方形
　\(\,\mathrm{EB=GC}\,\)
　\(\,\mathrm{∠PFD=90^{\circ}}\,\)
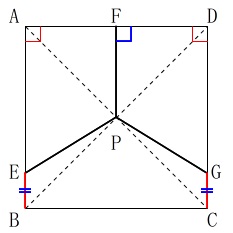このとき線分\(\,\mathrm{AE}\,\)と線分\(\,\mathrm{EB}\,\)の長さの比を求めます。

線分比を求めるのに線分の長さは1つもありません。
ということは、
　正方形の長さは何でも良い。
ということです。

「一般的に成り立つ。」ということですね。

一般的に成り立つということは、
具体的に長さをおいても成り立たなければなりません。

理由を記述する問題ではないのでどちらでも良いですよ。

一応、解説なので一般的に扱ってみます。

\(\,\mathrm{P}\,\)は正方形の対角線なので、
　\(\displaystyle \,\mathrm{FP=\frac{1}{2}\,AB}\,\)

できるだけ分数をさけたいので
　\(\,\mathrm{FP}=\color{red}{a}\,\)
　\(\,\mathrm{AB=AD}=\color{red}{2a}\,\)
としておきます。（\(\,a\,＞\,0\,\)です。）
※
本当は\(\,3\,\)の倍数の\(\,6a\,\)としたいところです。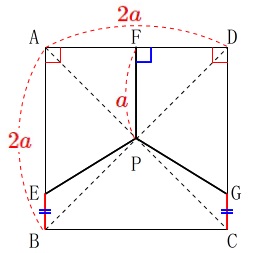正方形を三等分するので、
四角形\(\,\mathrm{AEPF}\,\)が正方形の\(\,\displaystyle \frac{1}{3}\,\)になれば良いのです。
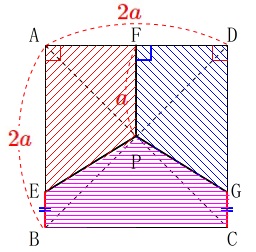そのときは四角形\(\,\mathrm{DGPF}\,\)も合同で等しくなるので、
残りの五角形も同じ面積になります。

\(\,\mathrm{EB}=x\,\)とおくと
　\(\hspace{4pt}\mathrm{AE}=\color{blue}{2a-x}\)
台形\(\,\mathrm{AEPF}\,\)の高さは
　\(\,\hspace{4pt}\mathrm{AF}=\color{red}{a}\,\)
なので台形\(\,\mathrm{AEPF}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S_1&=&\frac{\{a+(2a-x)\}\times a}{2}\\
&=&\frac{a(3a-x)}{2}
\end{eqnarray}\)

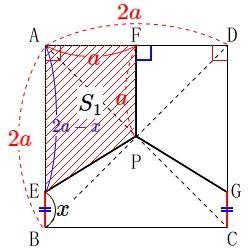
正方形\(\,\mathrm{ABCD}\,\)の面積は\(\,4a^2\,\)なので
　\(\begin{eqnarray}\displaystyle
\frac{a(3a-x)}{2}&=&\frac{1}{3}\times 4a^2\\
3a(3a-x)&=&2\times 4a^2\\
9a^2-3ax&=&8a^2\\
a^2-3ax&=&0\\
a(a-3x)&=&0\\
\end{eqnarray}\)

\(\,a\,＞\,0\,\)なので
　\(\hspace{4pt}\displaystyle x=\frac{1}{3}\,a\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:EB}&=&(2a-x):x\\
&=&\left(\,2a-\frac{1}{3}\,a\,\right):\frac{1}{3}\,a\\
&=&\frac{5}{3}\,a:\frac{1}{3}\,a\\
&=&\underline{　5:1　}
\end{eqnarray}\)

具体的な数値で求めるなら正方形の\(\,1\,\)辺は\(\,6\,\)が良いです。
三等分することと\(\,\mathrm{EP}\,\)は正方形の\(\,1\,\)辺の半分だから整数のまま処理できます。

\(\,\mathrm{EB}=x\,\)とすると\(\,\mathrm{AE}=6-x\,\)なので
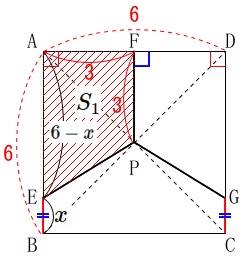台形\(\,\mathrm{AEPF}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S_1&=&\frac{\{3+(6-x)\}\times 3}{2}\\
&=&\color{blue}{\frac{3(9-x)}{2}}
\end{eqnarray}\)

これが正方形\(\,\mathrm{ABCD}\,\)の面積は\(\,\color{red}{36}\,\)を三等分するので、
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{3(9-x)}{2}}&=&\color{red}{12}\\
3(9-x)&=&24\\
9-x&=&8\\
x&=&1　（適）
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:EB}&=&(6-x):x\\
&=&\underline{　5:1　}
\end{eqnarray}\)

(3)
三角形を三等分する作図をします。
ただし、単に重心で三等分する問題ではありません。

条件を整理しておきます。

　\(\,\mathrm{△ABC}\,\)の各辺から等しい距離にある点を\(\,\mathrm{Q}\,\)
　点\(\,\mathrm{E,F}\,\)はそれぞれ\(\,\mathrm{BC,CA}\,\)上の点
　線分\(\,\mathrm{BQ,EQ,FQ}\,\)で\(\,\mathrm{△ABC}\,\)を三等分する。
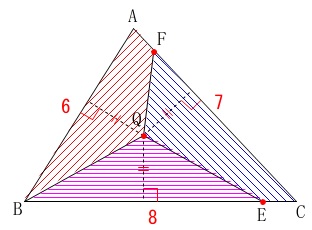長さがあるので面積も具体的に求まりますが、
必要ありません。

先ずは\(\,\mathrm{Q}\,\)を定めましょう。

\(\,2\,\)辺と距離の等しい点の集まりが角の二等分線です。
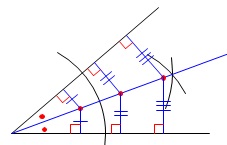つまり、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{△ABC}\,\)の各頂点の角の二等分線の交点です。
（「内心」といいますが、ここでは使いません。）
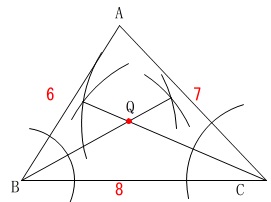このとき三つ目の角の二等分線は必ず点\(\,\mathrm{Q}\,\)を通るので、
三つ目の角の二等分線は引かなくても良いです。

点\(\,\mathrm{Q}\,\)の作図は終わりました。
これは解答の一部です。

残りは\(\,\mathrm{△ABC}\,\)を三等分するように\(\,\mathrm{E,F}\,\)を作図します。

ここで点\(\,\mathrm{Q}\,\)は、
　\(\,\mathrm{△ABC}\,\)の各辺からの距離が等しい。
ことを思い出してください。

点\(\,\mathrm{Q}\,\)と各辺との距離は、
点\(\,\mathrm{Q}\,\)と\(\,\mathrm{△ABC}\,\)の頂点を結んだ三角形3つの高さになっています。
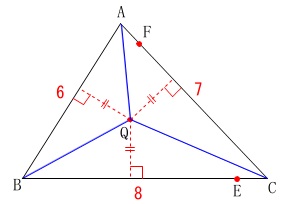ここでこの距離を\(\,a\,\)とすると、
（習慣的に\(\,r\,\)とするのですが\(\,a\,\)としておきます。）
　\(\begin{eqnarray}\displaystyle
\mathrm{△QAB}&=&\frac{1}{2}\times 6\times a\\
&=&3a
\end{eqnarray}\)
のように、\(\,\mathrm{△QBC,△QCA}\,\)の面積を出していくのが普通なのですが、
比が出せれば良いので高さを適当な数字でおいても構いません。

ここでは高さを文字でも数字でもおきません。
高さは同じだということで、
面積比だけを考えます。

高さが同じなので、
　\(\,\mathrm{△QAB:△QBC:△QCA}\,\)
は底辺の比と同じで
　\(\hspace{10pt}\mathrm{△QAB:△QBC:△QCA}\\
=\large{\color{blue}{⑥}}:\large{\color{blue}{⑧}}:\large{\color{blue}{⑦}}\,\)
となっています。
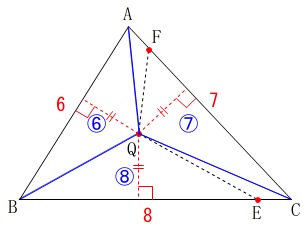面積を合わせると、
　\(\,\mathrm{△ABC=\color{blue}{6}+\color{blue}{8}+\color{blue}{7}=\color{red}{21}}\,\)
となるのでこれを三等分したとき、
1つの図形は\(\,\color{red}{7}\,\)となれば良いのです。

\(\,\mathrm{△QCA}=\color{blue}{⑦}\,\)を1つの図形にするなら、
そのまま使えますが、
この問題では\(\,\mathrm{E,F}\,\)は\(\,\mathrm{BC,CA}\,\)上にとるように指示されています。

三角形で分けられるのは\(\,\mathrm{△QBE}\,\)で、
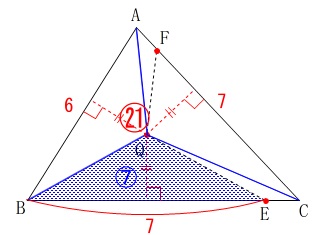この底辺を\(\,\color{red}{7}\,\)にすれば三等分された図形が1つ決まります。

底辺としたい\(\,\color{red}{7}\,\)は辺\(\,\mathrm{CA}\,\)と同じなので、
コンパスで\(\,\mathrm{CA}\,\)の長さをとり、
\(\,\mathrm{B}\,\)から円をかけば\(\,\color{red}{7}\,\)の位置が決まります。
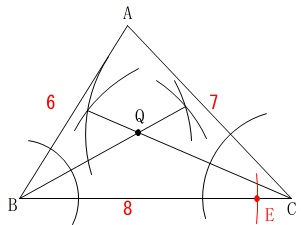これも作図の一部です。

このとき、図形が切り分けられています。
　\(\,\mathrm{△QBE:△QEC=\color{blue}{⑦}:\color{blue}{①}}\,\)
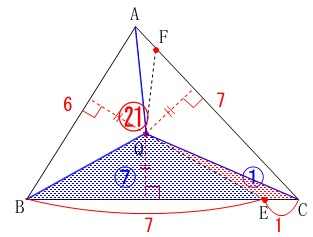ここまで来るとだいぶ見えてくるでしょう。

残りの面積を二等分することを考えると、
　\(\,\mathrm{△QCF=\color{blue}{⑥}\,,\,△QAF=\color{blue}{①}}\,\)
となれば、
　\(\,\mathrm{四角形\,QECF=\color{red}{⑦}}\,\)
　\(\,\mathrm{四角形\,QFAB=\color{magenta}{⑦}}\,\)
となり、\(\,\mathrm{△ABC}\,\)は三等分されます。
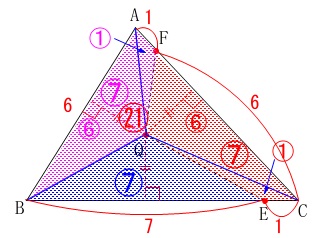\(\,\mathrm{CF=\color{red}{6}}\,\)の作図は、
辺\(\,\mathrm{AB}\,\)に\(\,\color{red}{6}\,\)があるので\(\,\mathrm{AB}\,\)の長さをコンパスでとり、
\(\,\mathrm{C}\,\)を中心に円をかけば\(\,\mathrm{F}\,\)が定まります。
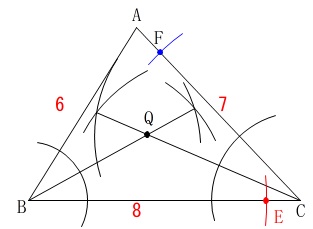線分\(\,\mathrm{BQ,EQ,FG}\,\)も作図するよう指示があるので、
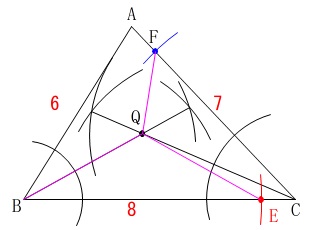この問題の作図は以上です。

作図の手順を簡単にまとめると、
　\(\,\mathrm{∠ABC}\,\)の二等分線を引く。
　\(\,\mathrm{∠ACB}\,\)の二等分線を引く。
　2つの角の二等分線の交点を\(\,\mathrm{Q}\,\)とする。
　線分\(\,\mathrm{AC}\,\)を半径にして\(\,\mathrm{B}\,\)を中心に円をかく。
　辺\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{E}\,\)とする。
　線分\(\,\mathrm{AB}\,\)を半径にして\(\,\mathrm{C}\,\)を中心に円をかく。
　辺\(\,\mathrm{AC}\,\)との交点を\(\,\mathrm{F}\,\)とする。
となります。

三角形を三つの三角形で等分するなら重心となります。
しかし、三等分だけの条件だと少し違ってきます。

\(\,\mathrm{△QAC}\,\)を三等分の1つだとすると、
\(\,\mathrm{AC}\,\)上の\(\,1\,\)点を決めれば三等分できます。

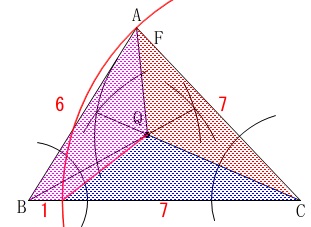
この問題はそれでは足りないということで、
わざわざ\(\,\mathrm{E,F}\,\)を\(\,\mathrm{BC,CA}\,\)上という条件付きで出題されていました。

定義を確認し、意味を知ってしまえば大したことではないですけど、
この問題は全国でも知っておきたい作図問題です。

滋賀の公立入試は甘くは無いですね。
特に上位校を狙うとなると厳しい入試です。

彦根城とか琵琶湖が強い印象になっていますが、
県境を越えるとそこは京都市なのですよ。

以上です。

⇒　滋賀県公立高校入試数学の問題と解説

中学数学全般の基本を意味をおさえながら定着させることが大切です。