2021年度東京都公立高校入試問題【前期】の数学の過去問解説

東京都公立高校入試問題2021年(令和3年)度【前期】の数学の過去問解説です。
三平方の定理は出題範囲から除外されていますので計算量も多くはありません。
都立入試数学は例年かたよりのないバランスの良い問題構成で、
基本中心ですがしっかりと手を動かさないと高得点は難しいでしょう。

東京都公立高校入試の数学2021年（令和3年）度の問題

都立入試2021年度の問題です。

⇒　2021年度都立入試数学の問題

例年と同じように分野の偏りは少ないバランスの良い問題構成です。
出題範囲から除外された三平方の定理以外においては復習にも良いですね。

東京都公立高校入試の数学2021年（令和3年）度の解説

三平方の定理は出題範囲から除外されています。
その代わりに他の分野は掘り下げられるのですが、
基本中心であることには変わりません。

第１問

計算問題、方程式、関数、作図などの基本小問集合ですが、
１問１問の配点が低いわけではありませんよ。

\(\color{black}{\fbox{　1　}}\)

〔問１〕
計算順序に気をつければ良いだけです。

　\(\hspace{10pt}\displaystyle \color{red}{-3^2\times \frac{1}{9}}+8\\
=\color{red}{-1}+8\\
=\,\underline{　7　}\,\)

足し算引き算より、掛け算割り算が先です。

〔問２〕
分母を１つにして、（通分して）
分子の計算に集中します。

　\(\hspace{10pt}\displaystyle \frac{5a-b}{2}-\frac{a-7b}{4}\\
\displaystyle =\frac{\color{red}{2(5a-b)-(a-7b)}}{4}\\
\displaystyle =\frac{\color{red}{10a-2b-a+7b}}{4}\\
\displaystyle =\,\underline{　\frac{9a+5b}{4}　}\,\)

分子には（かっこ）がついていることに注意しておきましょう。

〔問３〕
無理数の計算です。
有理数計算と同じように割り算は逆数の掛け算です。

　\(\hspace{10pt}3\div \sqrt{6}\times \sqrt{8}\\
\displaystyle =\frac{3\times \sqrt{8}}{\sqrt{6}}\\
\displaystyle =\frac{3\times \color{red}{\sqrt{4}}}{\sqrt{3}}\\
\displaystyle =\frac{\color{blue}{3}\times \color{red}{2}}{\color{blue}{\sqrt{3}}}\\
=\,\underline{　2\sqrt{3}　}\,\)

無理数どうしは中身で約分できます。
４行目から５行目は有理化でも良いです。
　\(\hspace{10pt}\displaystyle \frac{3\times 2}{\sqrt{3}}\\
\displaystyle =\frac{6\times \color{magenta}{\sqrt{3}}}{\sqrt{3}\times \color{magenta}{\sqrt{3}}}\\
\displaystyle =\frac{6\sqrt{3}}{3}\\
=2\sqrt{3}\)

〔問４〕
方程式は左辺にすべての項を集めることが基本ですが、
１次方程式では定数項を右辺に集めます。

　\(\begin{eqnarray}\displaystyle
-4x+2&=&9(x-7)\\
-4x+2&=&9x-63\\
-4x-9x&=&-2-63\\
-13x&=&-65\\
x&=&5
\end{eqnarray}\)

答え　\(\,\underline{　x=5　}\,\)

〔問５〕
連立方程式を解きます。
どちらかの係数をそろえる加減法でも良いですが、
代入法が早そうです。

第１の方程式から
　\(\begin{eqnarray}
5x+y&=&1\\
y&=&\color{red}{1-5x}　･･･①
\end{eqnarray}\)

これを第２の方程式に代入すると
　\(\begin{eqnarray}\displaystyle
-x+6\color{red}{y}&=&37\\
-x+6(\color{red}{1-5x})&=&37\\
-x+6-30x&=&37\\
-x-30x&=&37-6\\
-31x&=&31\\
x&=&\color{blue}{-1}
\end{eqnarray}\)

このとき\(\,①\,\)から
　\(\begin{eqnarray}
y&=&1-5\color{blue}{x}\\
&=&1-5(\color{blue}{-1})\\
&=&1+5\\
&=&6
\end{eqnarray}\)

答え　\(\,\underline{　x=-1\,,\,y=6　}\,\)

連立方程式を解くときは一文字消去が基本です。

〔問６〕
２次方程式を解きます。
まとまりを先に求めるか展開するかですが、
どちらでも構いません。

　\(\begin{eqnarray}\displaystyle
(x+8)^2&=&2\\
x+8&=&\pm \sqrt{2}\\
x&=&\,\underline{\,-8\pm \sqrt{2}\,}\,
\end{eqnarray}\)

展開すると解の公式を利用することになります。

　\(\begin{eqnarray}\displaystyle
(x+8)^2&=&2\\
x^2+16x+64&=&2\\
x^2+16x+62&=&0\\
\end{eqnarray}\)

因数分解できないので解の公式から
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-16\pm \sqrt{16^2-4\cdot 1\cdot 62}}{2\times 1}\\
&=&\frac{-16\pm \sqrt{256-248}}{2}\\
&=&\frac{-16\pm \sqrt{8}}{2}\\
&=&\frac{-16\pm 2\sqrt{2}}{2}\\
&=&-8\pm \sqrt{2}
\end{eqnarray}\)

１次の項の係数が偶数なので
　\(\hspace{10pt}ax^2+2b’x+c=0\)
のとき
　\(\hspace{4pt}\displaystyle x= \frac{-b’\pm \sqrt{(b’)^2-ac}}{a}\)
から
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-8\pm \sqrt{8^2-62}}{1}\\
&=&-8\pm \sqrt{2}
\end{eqnarray}\)
とするのも良いですが、
こちらの公式を覚えている人は平方された形を利用しているでしょう。

〔問７〕
２次関数の変域を求めます。

　\(\hspace{4pt}y=-3\,x^2\,(-4\,≦\,x\,≦\,1)\)

グラフを簡単に書いて確認すれば問題ありません。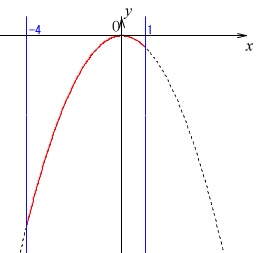最小値は\(\,x=-4\,\)、
最大値は\(\,x=0\,\)のときです。
（\(\,x=1\,\)のときは\(\,y\,\)の変域には関係しません。）

\(\,x=-4\,\)のとき

　\(\begin{eqnarray}\displaystyle
y&=&-3\times (-4)^2\\
&=&-48
\end{eqnarray}\)

\(\,x=0\,\)のときは\(\,y=0\,\)なので
求める\(\,y\,\)の変域は

　\(\hspace{4pt}\color{black}{\fbox{\(\,-48\,\)}}≦y≦\color{black}{\fbox{\(\,0\,\)}}\)

答え　\(\,①\,ア\,　\,②\,オ\)

〔問８〕
さいころ２つ投げたときの確率を求めます。

　大きいさいころの出た目を\(\,\color{red}{a}\,\)
　小さいさいころの出た目を\(\,\color{blue}{b}\,\)
としたときの
　\(\hspace{4pt}\color{red}{a}\,≧\,\color{blue}{b}\)
となる確率です。

樹形図で良いですが表で説明しておきます。

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\,\color{red}{1}\, & ○ & & & & & \\ \hline
\color{red}{2} & ○ & ○ & & & & \\ \hline
\color{red}{3} & ○ & ○ & ○ & & & \\ \hline
\color{red}{4} & ○ & ○ & ○ & ○ & & \\ \hline
\color{red}{5} & ○ & ○ & ○ & ○ & ○ & \\ \hline
\color{red}{6} & ○ & ○ & ○ & ○ & ○ & ○\\ \hline
\end{array}\)

\(\,a=1\,\)のとき\(\,b=1\,\)の\(\,1\,\)通り
\(\,a=2\,\)のとき\(\,b=1\,,\,2\,\)の\(\,2\,\)通り
　\(\hspace{4pt}\cdots\)
と見ていくと\(\,36\,\)通りのうち、
合計で\(\,21\,\)通りで\(\,a\,≧\,b\,\)となります。

　\(\hspace{10pt}\displaystyle \frac{21}{36}=\,\underline{　\frac{7}{12}　}\,\)

答え　\(\,あ\,7\,,\,い\,1\,,\,う\,2\,\)

〔問９〕
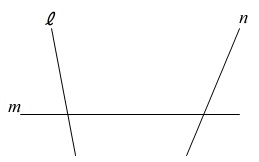
３直線から等しい距離にある点の作図です。

問題に条件が無ければいくつかありますが、
この問題では図の直線\(\,m\,\)の上側にある点\(\,\mathrm{P}\,\)を作図します。
２直線から等しい距離にある点の集まりは
　「角の二等分線」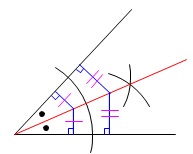
なので３直線から等しい距離にある点は、
　「（２つの）角の二等分線の交点」
になります。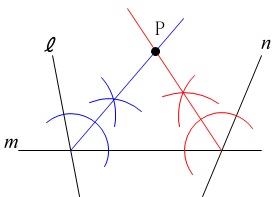この場合は、
　２直線\(\,\ell\,,\,m\,\)の角の二等分線
と
　２直線\(\,m\,,\,n\,\)の角の二等分線
で作図していますが答えとなる図です。

直線\(\,\ell\,,\,n\,\)（三つ目）の二等分線は描かなくても必ず交点は一致します。

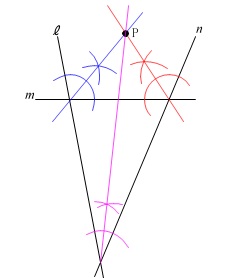
点\(\,\mathrm{P}\,\)は３直線\(\,\ell\,,\,m\,,\,n\,\)を接線とする、
円の中心（傍心「ぼうしん」）です。直線\(\,m\,\)の上側という条件が無ければ、
３直線から等しい距離にある点は他にもあることを確認しておくと良いです。

当会の教材を使っている人は『覚え太郎』（平面幾何）で詳しく取り上げているので確認しておきましょう。

\(\color{black}{\fbox{　1　}}\)は以上です。

第２問

例年通り生徒と先生の問題を考えます。

　\(\color{black}{\fbox{　2　}}\)

〔問１〕
先生が示した問題です。
正方形のタイルの半分が色づけされているので、
図形の処理で関係性が見えてきます。

図１において元の正方形の半分が色づけされています。
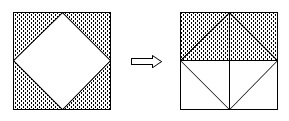図２は図１を集めただけなので、
大きな正方形の半分が色づけされています。

また図３は図１と同じで、
大きな正方形の半分が色づけされています。

だから図２と図３は大きさ正方形の１辺が同じ長さなので、
同じ面積になります。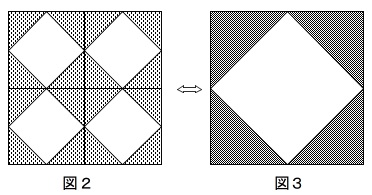この関係は\(\,n=5\,\)としても同じです。

小さな正方形の１辺は\(\,2a\,\)なので、
\(\,n=5\,\)のとき大きな正方形の１辺は
　\(\hspace{4pt}2a\times 5=10a　\mathrm{(cm)}\)

\(\,\mathrm{P\,,\,Q}\,\)は大きな正方形の半分の面積で等しく

　\(\begin{eqnarray}\displaystyle
\mathrm{P}&=&\mathrm{Q}\\
&=&\frac{1}{2}\times (10a)^2\\
&=&\,\underline{　50\,a^2　}\,　\mathrm{(cm^2)}
\end{eqnarray}\)

答え　\(\,\mathrm{①イ　②ウ}\,\)

記号は違いますが面積は等しいことに注意しておきましょう。

〔問２〕
今度は正方形の中に円があります。
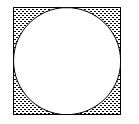問１と同じように\(\,n\,\)枚の正方形を並べ、
色つきの部分の面積が等しくなることを証明します。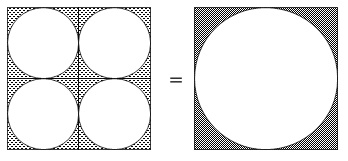
図形の移動で等しいことは示せませんが、
数式の計算で等しくなることを証明します。
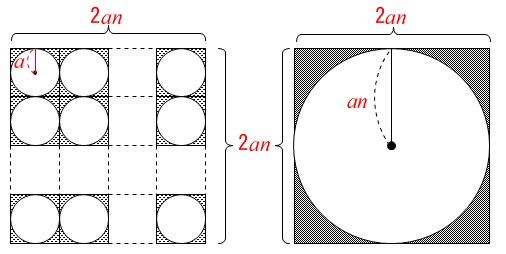小さな正方形が\(\,n^2\,\)個あることに注意しましょう。

（証明）
\(\,\mathrm{X}\,\)は１辺\(\,2an\,\)の正方形の面積から、
半径\(\,a\,\)の円の面積を\(\,n^2\,\)個引いたものなので
　\(\begin{eqnarray}\displaystyle
\mathrm{X}&=&(2an)^2-\pi\,a^2\times n^2\\
&=&4a^2n^2-\pi\,a^2n^2\\
&=&(4-\pi)a^2n^2　
\end{eqnarray}\)

また、
\(\,\mathrm{Y}\,\)は１辺\(\,2an\,\)の正方形の面積から、
半径\(\,an\,\)の円の面積を引いたものなので
　\(\begin{eqnarray}\displaystyle
\mathrm{Y}&=&(2an)^2-\pi\,(an)^2\\
&=&4a^2n^2-\pi\,a^2n^2\\
&=&(4-\pi)a^2n^2
\end{eqnarray}\)

よって、
　\(\,\mathrm{X=Y}\,\)（終わり）

証明の書き方は気にしなくても、
結果同じ文字式になっていれば大丈夫です。

第３問

関数の問題ですが、最後は図形の要素を含む問題です。
前半で長くなっているので説明は簡単に済ませます。

　\(\color{black}{\fbox{　3　}}\)

先に条件をまとめておきます。

　点\(\,\mathrm{A}\,\)の座標は\(\,(\,-12\,,\,-2\,)\,\)
　直線\(\,\ell\,\)：\(\,y=-2x+14\,\)
　点\(\,\mathrm{B}\,\)は直線\(\,\ell\,\)の\(\,y\,\)切片
　点\(\,\mathrm{P}\,\)は直線\(\,\ell\,\)上の点
　直線\(\,m\,\)は\(\,2\,\)点\(\,\mathrm{A\,,\,P}\,\)を通る。
直線\(\,\ell\,\)の\(\,x\,\)軸との交点（\(\,x\,\)切片）は、
固定されていますので書き込んでおいても良いですね。

〔問１〕
「点\(\,\mathrm{P}\,\)の\(\,y\,\)座標が\(\,10\,\)のとき」
点\(\,\mathrm{P}\,\)は直線\(\,\ell\,\)上の点なので\(\,x\,\)座標は

　\(\begin{eqnarray}\displaystyle
10&=&-2x+14\\
2x&=&14-10\\
x&=&\,\underline{　2　}\,
\end{eqnarray}\)

〔問２〕
\(\,2\,\)点を通る直線の式を求めます。

「点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,4\,\)のとき」
点\(\,\mathrm{P}\,\)の\(\,y\,\)座標は
　\(\begin{eqnarray}\displaystyle
y&=&-2x+14\\
&=&-2(4)+14\\
&=&6
\end{eqnarray}\)
なので点\(\,\mathrm{P}\,\)の座標は
　\(\,\mathrm{P\,(\,4\,,\,6\,)}\,\)

直線\(\,m\,\)は\(\,2\,\)点\(\,\mathrm{A\,,\,P}\,\)を通ります。

　\(\,\mathrm{A\,(\,-12\,,\,-2\,)\,}\,\)
　\(\,\mathrm{P\,(\,4\,,\,6\,)}\,\)
を通る直線\(\,m\,\)の傾きは
　\(\hspace{4pt}\displaystyle \frac{6-(-2)}{4-(-12)}=\frac{8}{16}=\frac{1}{2}\)

直線\(\,m\,\)は
　\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x+b\)
とおけて\(\,\mathrm{P\,(\,\color{red}{4}\,,\,\color{blue}{6}\,)}\,\)を通ることから
（\(\,\mathrm{A}\,\)でも良いです。）

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\,x+b\\
\color{blue}{6}&=&\frac{1}{2}\times \color{red}{4}+b\\
b&=&6-2\\
&=&4
\end{eqnarray}\)

よって\(\,m\,\)の式は
　\(\hspace{4pt}\displaystyle y=\color{black}{\fbox{　\(\,\frac{1}{2}\,\)　}}\,x+\color{black}{\fbox{　4　}}\)

〔問３〕
条件にしたがって２つの三角形の面積が
等しくなるときの点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。

条件
　点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,7\,\)より大きい。
　点\(\,\mathrm{P}\,\)を\(\,x\,\)軸を対称の軸として線対称移動した点が\(\,\mathrm{Q}\,\)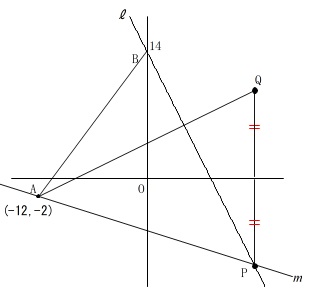
このとき、
　\(\,\mathrm{△APB\,=\,△APQ}\,\)
となる点\(\,\mathrm{P}\,\)の座標を求めます。

底辺となる辺を共通の辺\(\,\mathrm{AP}\,\)とすると、
　「点\(\,\mathrm{B}\,\)と点\(\,\mathrm{Q}\,\)から\(\,m\,\)までの距離（高さ）が同じ」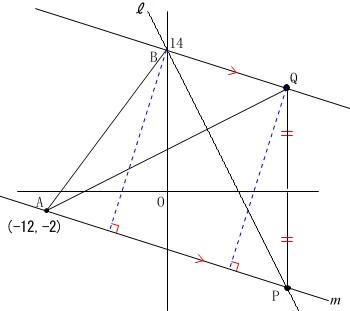
になるとき面積が等しくなるので、
　「直線\(\,\mathrm{AP}\,\)と直線\(\,\mathrm{BQ}\,\)が平行」
つまり
　「直線\(\,\mathrm{AP}\,\)と\(\,\mathrm{BQ}\,\)の傾きが同じ。」
になるときの点\(\,\mathrm{P}\,\)の座標を求めれば良いのです。

「点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,7\,\)より大きい数」
という条件は、
　直線\(\,\ell\,\)と\(\,x\,\)軸との交点より右側
ということです。

点\(\,\mathrm{P}\,\)の座標を文字設定して求めましょう。

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
点\(\,\mathrm{P}\,\)は\(\,\ell\,\)上の点なので
　\(\,\mathrm{P}\,(\,t\,,\,-2t+14\,)\)
このとき、
　\(\hspace{4pt}t＞7　･･･①\)

点\(\,\mathrm{Q}\,\)は点\(\,\mathrm{P}\,\)を\(\,x\,\)軸で線対称移動した点なので
\(\,x\,\)座標は同じで\(\,y\,\)座標の符号が入れかわります。
　\(\hspace{4pt}\mathrm{Q}\,(\,t\,,\,2t-14\,)\)

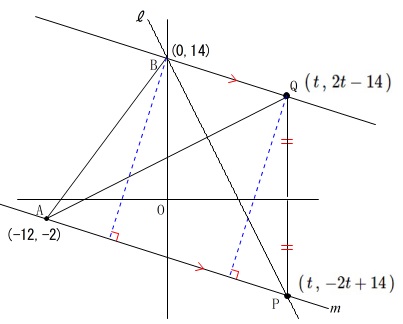
２点\(\,\mathrm{A\,,\,P}\,\)を結ぶ直線\(\,m\,\)の傾きは
　\(\hspace{4pt}\mathrm{A}\,(-12\,,\,-2\,)\)
　\(\hspace{4pt}\mathrm{P}\,(\,t\,,\,-2t+14\,)\)
から
　\(\hspace{10pt}\displaystyle \frac{-2t+14-(-2)}{t-(-12)}\\
\displaystyle =\frac{-2t+16}{t+12}　･･･②\)

２点\(\,\mathrm{B\,,\,Q}\,\)を結ぶ直線の傾きは
　\(\hspace{4pt}\mathrm{B}\,(0\,,\,14\,)\)
　\(\hspace{4pt}\mathrm{Q}\,(\,t\,,\,2t-14\,)\)
から
　\(\hspace{10pt}\displaystyle \frac{2t-14-(14)}{t-(0)}\\
\displaystyle =\frac{2t-28}{t}　･･･③\)

\(\,②\,\)と\(\,③\,\)が等しいときなので
　\(\begin{eqnarray}\displaystyle
\frac{-2t+16}{t+12}&=&\frac{2t-28}{t}\\
t(-2t+16)&=&(t+12)(2t-28)\\
t(-t+8)&=&(t+12)(t-14)\\
-t^2+8t&=&t^2-2t-168\\
\end{eqnarray}\)

両辺の項を左辺に集めると、
　\(\begin{eqnarray}\displaystyle
2t^2-10t-168&=&0\\
t^2-5t-84&=&0\\
(t-12)(t+7)&=&0
\end{eqnarray}\)

これから
　\(\hspace{10pt}t=12\,,\,-7\)
となりますが\(\,①\,(t＞7)\,\)から
　\(\hspace{10pt}t=12\)

よって求める点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は
　\(\hspace{10pt}x=\,\underline{　12　}\,\)

条件を整理した後は、
２次方程式の計算に集中しましょう。

第３問〔問３〕別解

\(\,\mathrm{△APQ}\,\)の面積は\(\,\mathrm{PQ}\,\)を底辺とみて
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times (\color{red}{4t-28})\times (\color{blue}{t+12})\\
&=&(2t-14)(t+12)\\
&=&2(t-7)(t+12)
\end{eqnarray}\)と計算しやすいですが、
\(\,\mathrm{△ABP}\,\)の面積は直線\(\,\mathrm{AP}\,\)の切片を求めるか、
『超え太郎』の知識が必要になるので利用しませんでした。

しかし、\(\,\mathrm{△ABP}\,\)を\(\,y\,\)軸方向に\(\,+2\,\)平行移動した三角形を、
\(\,\mathrm{△A’B’P’}\,\)とすると
　\(\hspace{10pt}\mathrm{P’}\,(t\,,\,-2t+16\,)\)
となるので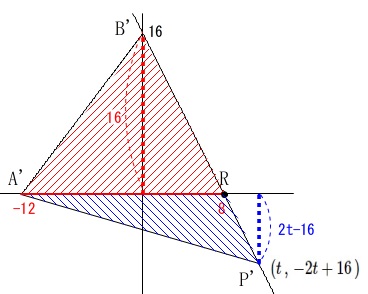直線\(\,\ell\,\)と\(\,x\,\)軸との交点を\(\,\mathrm{R}\,\)とすると、
図の\(\,\mathrm{A’R}\,\)を底辺とする２つの三角形の面積の和から
　\(\begin{eqnarray}\displaystyle
\mathrm{△A’B’P’}&=&\mathrm{\color{red}{△A’B’R}+\color{blue}{△A’P’R}}\\
&=&\frac{1}{2}\times 20\times (\color{red}{16}+\color{blue}{2t-16})\\
&=&20\,t
\end{eqnarray}\)

\(\,\mathrm{△APQ}\,\)の面積と\(\,\mathrm{△A’B’P}\,\)の面積が等しいときなので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\mathrm{△A’B’P}\\
2(t-7)(t+12)&=&20t\\
(t-7)(t+12)&=&10t\\
t^2+5t-84&=&10t\\
t^2-5t-84&=&0\\
(t+7)(t-12)&=&0\\
t&=&-7\,,\,12
\end{eqnarray}\)

となり同じ結果が出てきます。

なぜ平行移動したかというと、
座標上での図形、特に三角形の面積は、
　「底辺を軸に平行に」
取って見たかったからです。

こちらの方が計算が楽なようにも感じますが、
平行移動させて２つの三角形の底辺を別に見るというのは、
試験中は難しいかもしれませんね。

でも、「三角形の面積は平行移動しても変わらない。」
ということは覚えておくと良いです。

第４問

円と内接する長方形の平面図形の問題です。

　\(\color{black}{\fbox{　4　}}\)

条件
　四角形\(\,\mathrm{ABCD}\,\)は長方形
　点\(\,\mathrm{O}\,\)は円の中心
　線分\(\,\mathrm{AC}\,\)は円の直径
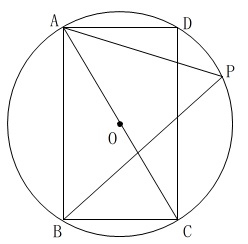先ずは角度の問題です。

〔問１〕
\(\,∠\mathrm{ABP}=a^{\circ}\,\)とするときの\(\,\mathrm{∠PAC}\,\)の大きさです。
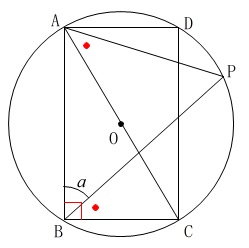円周角の定理から
　\(\,\mathrm{∠PAC=∠PBC}\,\)

また\(\,\mathrm{∠ABC}\,\)は長方形の１つの内角なので\(\,90^{\circ}\)だから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ABP+∠PBC}&=&90^{\circ}\\
\mathrm{∠PBC}&=&90^{\circ}-\mathrm{∠ABP}\\
\mathrm{∠PAC}&=&90^{\circ}-\mathrm{∠ABP}\\
&=&\,\underline{　(90-a)　度}\,　
\end{eqnarray}\)

答え　\(\,\underline{　イ　}\,\)

〔問２〕
条件が加わります。

　交点は図にある通り\(\,\mathrm{Q\,,\,R}\,\)
　\(\,\mathrm{AB=AP}\,\)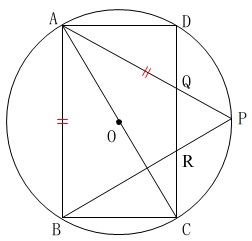
\(\,①\,\)
\(\,\mathrm{△QRP}\,\)が二等辺三角形であることの証明です。

図の中で済ませておくことがポイントです。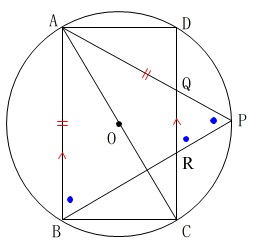
（証明）
　\(\,\mathrm{△QRP}\,\)において
仮定の\(\,\mathrm{AB=AP}\,\)から二等辺三角形の底角は等しく
　\(\begin{eqnarray}
\mathrm{\color{red}{∠ABP}}&=&\mathrm{∠APB}\\
&=&\mathrm{\color{blue}{∠QPR}}　･･･(\mathrm{1})
\end{eqnarray}\)
また長方形の対辺は平行なので同位角が等しく
　\(\hspace{4pt}\mathrm{\color{red}{∠ABP}=\color{blue}{∠QRP}}　･･･(\mathrm{2})\)
\(\,\mathrm{(1)\,,\,(2)}\,\)より
　\(\,\mathrm{∠QPR=∠QRP}\,\)
よって、２つの角が等しいので
　\(\,\mathrm{△QRP}\,\)は二等辺三角形である。
（終わり）

「二等辺三角形の底角が等しいこと」、
「平行線の同位角が等しいこと」、
この２つが言えてあればまとめ方は気にしなくて良いです。

\(\,\mathrm{②}\,\)
長さの条件が加わり、面積を求めます。

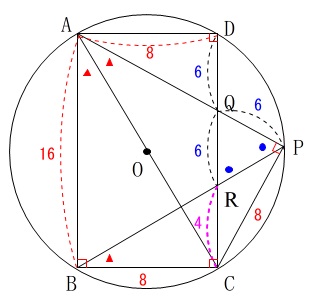
　\(\,\mathrm{AB=6\,,\,AD=8}\,\)
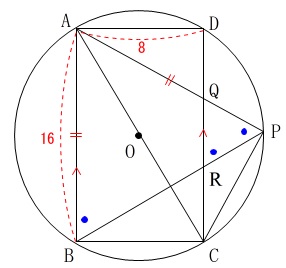単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。

このとき\(\,\mathrm{△PRC}\,\)の面積を求めます。

線分\(\,\mathrm{AC}\,\)は直径で直角三角形があるので
三平方の定理を使いたくなりますが使いません。
（試験範囲から除外されていることもありますが）

相似（合同）で十分です。

\(\,\mathrm{△ABC\,≡\,△APC}\,\)であることから
　\(\hspace{10pt}\mathrm{BC=PC}=\color{red}{8}\)

さらに、
\(\,\mathrm{△ADQ\,≡\,△CPQ}\,\)であることから
　\(\hspace{10pt}\mathrm{DQ=PQ}=\color{blue}{x}\)
とおくと\(\,①\,\)から\(\,\mathrm{△QRP}\,\)は二等辺三角形だから
　\(\hspace{10pt}\mathrm{QR}=\color{blue}{x}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{RC}&=&\mathrm{DC-DR}\\
&=&\color{magenta}{16-2x}
\end{eqnarray}\)
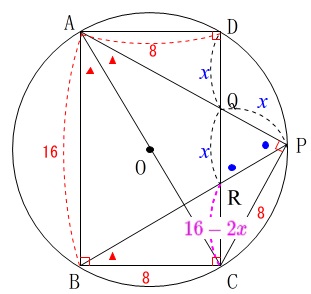ここで
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△BCR}\,\)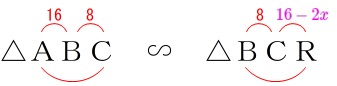なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:BC}&=&\mathrm{BC:CR}\\
16:8&=&8:(16-2x)\\
x&=&6
\end{eqnarray}\)
\(\,\mathrm{△CPQ}\,\)は直角三角形で
　\(\begin{eqnarray}\displaystyle
\mathrm{△CPQ}&=&\frac{1}{2}\times \mathrm{CP}\times \mathrm{QP}\\
&=&\frac{1}{2}\times 8\times 6\\
&=&24
\end{eqnarray}\)

\(\,\mathrm{△CPQ}\,\)の底辺を線分\(\,\mathrm{QC}\,\)と見ると
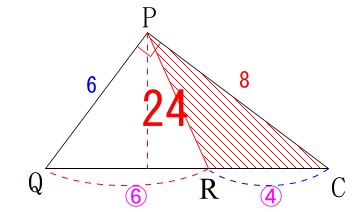\(\,\mathrm{△PQC}\,\)と\(\,\mathrm{△PRC}\,\)は高さが共通で底辺の比が
　\(\begin{eqnarray}\displaystyle
\mathrm{QC:RC}&=&(6+4):4\\
&=&10:4\\
&=&5:2
\end{eqnarray}\)

よって求める\(\,\mathrm{△PRC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△PRC}&=&\mathrm{△CPQ}\times \frac{2}{5}\\
&=&24\times \frac{2}{5}\\
&=&\,\underline{　\frac{48}{5}　}\,　(\mathrm{cm^2})
\end{eqnarray}\)

合同、相似な三角形がたくさんあるので、
どれを使うかはうまく整理していかないと迷う問題ですね。

第５問

立体の位置関係と体積の問題です。

　\(\color{black}{\fbox{　5　}}\)

三角柱にたくさんの条件がありますが、
図に書き込んでしまえば大したことはありません。

条件
　\(\,\mathrm{AB=4}\,\)
　\(\,\mathrm{AC=3}\,\)
　\(\,\mathrm{BC=5}\,\)
　\(\,\mathrm{AD=6}\,\)
　\(\,\mathrm{∠BAC=∠BAD=∠CAD=90^{\circ}}\,\)
　\(\,\mathrm{BP=FQ}\,\)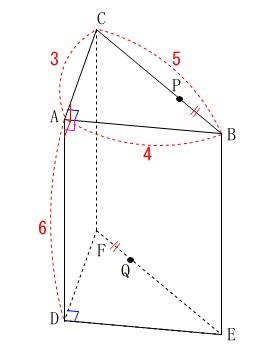
〔問１〕
\(\,\mathrm{BP=2}\,\)のとき、
直線\(\,\mathrm{PQ}\,\)となじれの位置にある辺の本数を求めます。

ねじれの位置とは、
　平行でも無く、交わりもしない。
位置関係にある直線です。

「直線」ですので注意することは１つだけ。
　「延長して交わるものはねじれの位置では無い。」
ということです。

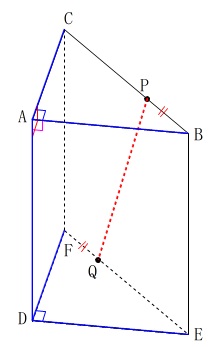
答え　\(\color{black}{\fbox{　5　}}\)　本

辺\(\,\mathrm{CF}\,\)と辺\(\,\mathrm{BE}\,\)は延長すると交わるので、
ねじれの位置ではありません。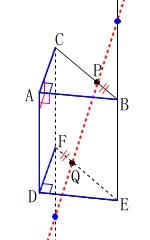

　〔問２〕
立体の体積を求めます。

　\(\,\mathrm{BP=4}\,\)のときの立体\(\,\mathrm{D-BPFQ}\,\)の体積
です。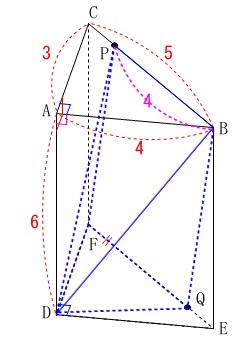
\(\,\mathrm{△DFE}\,\)において\(\,\mathrm{D}\,\)から\(\,\mathrm{FE}\,\)に垂線を下ろし、
線分\(\,\mathrm{DR}\,\)の長さを立体\(\,\mathrm{D-BPFE}\,\)の高さとします。
　\(\,\mathrm{△DEF}\,\)　∽　\(\,\mathrm{△RDF}\,\)　（∽　\(\,\mathrm{△RED}\,\)）
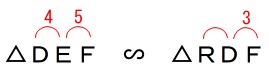なので、
　\(\begin{eqnarray}
\mathrm{DE:EF}&=&\mathrm{RD:DF}\\
4:5&=&\mathrm{RD}:3\\
5\,\mathrm{RD}&=&4\times 3\\
\mathrm{RD}&=&\frac{12}{5}
\end{eqnarray}\)

底面積は平行四辺形\(\,\mathrm{BPFQ}\,\)の面積で
　\(\hspace{10pt}\displaystyle 4\times 6\\
=24\)

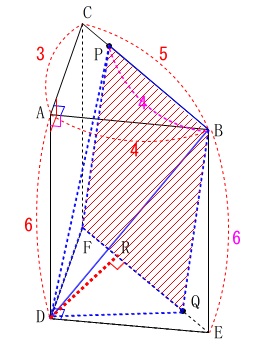
よって求める立体（すい体）の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 24\times \frac{12}{5}\\
&=&\,\underline{　\frac{96}{5}　}\,　(\mathrm{cm^3})
\end{eqnarray}\)

第５問の問２の別解

途中ですい体の高さを求めるときに相似を利用しました。

しかし、平行四辺形の\(\,\mathrm{F\,,\,Q}\,\)を\(\,\mathrm{E}\,\)側に\(\,\mathrm{1cm}\,\)移動させ、
長方形\(\,\mathrm{BPF’E}\,\)を底面とすると、
高さは同じなので同じ体積になります。

なので、立体\(\,\mathrm{D-BPF’E}\,\)の体積を求めておきます。
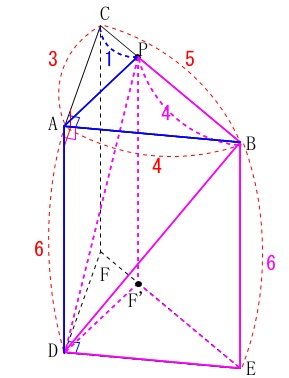\(\,\mathrm{△ABP}\,\)の面積は
\(\,\mathrm{△ABC}\,\)と高さは同じで底辺を\(\,5:4\,\)に分けているので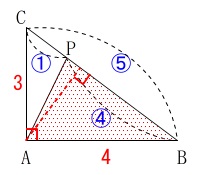
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABP}&=&\frac{4}{5}\times \mathrm{△ABC}\\
&=&\frac{4}{5}\times \frac{1}{2}\times 3\times 4\\
&=&\frac{24}{5}
\end{eqnarray}\)

三角柱\(\,\mathrm{ABP-DEF’}\,\)の体積は、
高さは同じ\(\,\color{red}{6}\,\)なので

　\(\hspace{10pt}\displaystyle \frac{24}{5}\times \color{red}{6}\\
\displaystyle =\frac{144}{5}\)

これから\(\,\mathrm{D-ABP}\,\)の三角錐の体積を引けば、
立体\(\,\mathrm{D-BPF’E}\,\)の体積になります。

三角錐\(\,\mathrm{D-ABP}\,\)の体積は、
　三角柱の\(\,\displaystyle \frac{1}{3}\,\)

なので三角柱から引いても良いですが、
残り\(\,\displaystyle \frac{2}{3}\,\)が求める体積\(\,V’\,\)になるので

　\(\begin{eqnarray}\displaystyle
V’&=&\frac{2}{3}\times \frac{144}{5}\\
&=&\,\underline{　\frac{96}{5}　}\,　(\mathrm{cm^3})
\end{eqnarray}\)

元の三角柱\(\,\mathrm{ABC-DEF}\,\)の体積が
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 4\times 3\times 6\\
=36\)

ここから比を利用して、
　\(\begin{eqnarray}\displaystyle
V’&=&36\times \frac{4}{5}\times \frac{2}{3}\\
&=&\frac{96}{5}　(\mathrm{cm^3})
\end{eqnarray}\)

としても良いです。

２０２１年度東京都公立高校入試の数学は以上です。

三平方の定理が除外され、
少し内容が濃くなっている感じはしますが、
基本的なことの繰り返しで対応できるというのは変わりないです。

対策ページでは無いですが一言付け加えておくと、
広い範囲でバランス良く問われているので、
基本の繰り返しは当然です。

しかし、基本の繰り返しの上に、
「直感的な見方をプラス」
できるくらいの練習をしておくと良いですね。

⇒　東京都公立高校入試数学の過去問と解答解説

例年偏った出題はされない東京都の数学です。