2021年度北海道公立高校入試数学(標準と学校裁量問題)の解説

２０２１年（令和３年）度北海道公立高校入試の数学の問題と解説です。
標準問題と学校裁量問題はどちらも５問構成ですが、
４問は共通なのでまとめて解説しておきます。
２０２１年度の入試ではいくつかの出題削除項目があります。
偏りのない出題が例年の北海道なので参考にするときはご注意ください。

2021年度北海道公立高校入試数学(標準および学校裁量)の問題

標準問題と学校裁量問題は４問が共通です。

標準問題の\(\color{black}{\fbox{2}}\)～\(\color{black}{\fbox{5}}\)が、
学校裁量問題の\(\color{black}{\fbox{1}}\)～\(\color{black}{\fbox{4}}\)になります。

標準問題

⇒　2021年度北海道公立入試数学の問題（標準問題）

\(\color{black}{\fbox{2}}\)～\(\color{black}{\fbox{5}}\)は学校裁量問題と共通問題になります。

学校裁量問題

⇒　2021年度北海道公立入試数学の問題（学校裁量問題）

標準問題の\(\color{black}{\fbox{　1　}}\)と学校裁量問題の\(\color{black}{\fbox{　5　}}\)が違います。

2021年度北海道公立高校入試数学(標準および学校裁量問題)の解説

２０２１年度の数学では、
　「相似な図形」「円周角の定理」
　「三平方の定理」「標本調査」
が削除された出題となっています。

標準問題の第１問の解説

\(\color{black}{\fbox{　1　}}\)

標準問題の\(\color{black}{\fbox{　1　}}\)です。

問１
計算問題が３つあります。

(1)
正の数負の計算の計算です。

　\(\hspace{10pt}3\color{red}{-(-6)}\\
=3\color{red}{+6}\\
=\,\underline{　9　}\,\)

ややこしい計算になっても、
（かっこ）を外す１行は書いた方が確実です。

(2)
分数計算が混じります。

　\(\hspace{10pt}\displaystyle 9\color{red}{\div \left(-\frac{1}{5}\right)}+4\\
=9\color{red}{\times (-5)}+4\\
=-45+4\\
=\,\underline{　-41　}\,\)

分数に限らず割り算は逆数の掛け算になります。

(3)
無理数の計算です。

　\(\hspace{10pt}\sqrt{28}-\sqrt{7}\\
=2\sqrt{7}-\sqrt{7}\\
=\underline{　\sqrt{7}　}\)

根号の中が同じときは、
ルートの前の数で足し算引き算ができます。

　\(\hspace{10pt}28=2^2\times 7\)
素因数分解はていねいにやった方が良いですよ。

問２
\(\,y\,\)が\(\,x\,\)に反比例している関数を選びます。

すべての関数を表しておきます。
　ア：\(\hspace{4pt}y=50\,x\)
　イ：\(\hspace{4pt}x\,y=300\)
　ウ：\(\hspace{4pt}y=100+x\)
　エ：\(\hspace{4pt}y=5\,\pi\,x^2\)

反比例を表す関数は
（比例定数を\(\,a\,\)とすると）
　\(\hspace{10pt}\displaystyle y=\frac{a}{x}\)
または
　\(\hspace{10pt}xy=a\)
と表される関数です。

イは変形すると
　\(\hspace{10pt}\displaystyle y=\frac{300}{x}\)

答え　\(\,\underline{　イ　}\,\)

問３
展開図を組み立てたとき、
平行で等しくなる線分を書き込みます。

組み立てたとき対角線\(\,\mathrm{AB}\,\)を含む面の対面にあって、
平行な対角線を書き込めば良いです。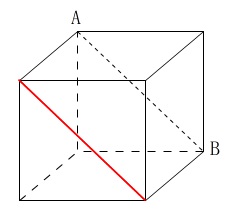
直感的に組み立てても良いですが、
線分\(\,\mathrm{AB}\,\)を含む面の下にある正方形が底面とすると、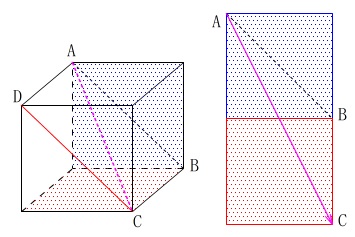
２つの正方形を組合わせ長方形の対角線になる\(\,\mathrm{AC}\,\)は、
立方体の対角線になります。

立体の対角線は、
　隣り合う２マスを組合わせた対角線になる２点
を結んだ線分です。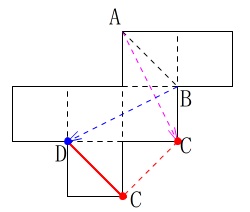対角線\(\,\mathrm{BD}\,\)は２つの正方形の対角線が１つしか無いので、
\(\,\mathrm{D}\,\)の位置が決まり、
立体を組んだときに\(\,\mathrm{C}\,\)が重なる点であることから答えが出ます。
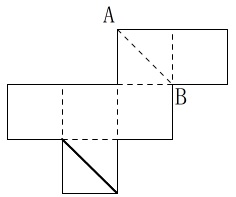下にある正方形を転がすと同じ立方体の展開図なので、
それから考えても良いです。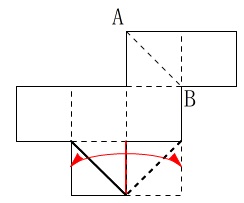\(\,\mathrm{C}\,\)と同じ点は、
２つの正方形を組合わせた対角線の移動を、
２回すれば元の点に戻ることから考えた人もいるでしょう。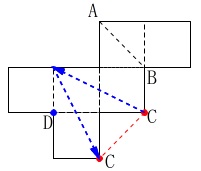時間のかかる問題ではないのでどっちでも良いです。

問４
直線の式を求めます。

　「\(\,y=3x\,\)に平行」
というのは傾きが同じだということなので
　\(\hspace{10pt}y=3x+b\)
とおけて、
　「点\(\,(\,0\,,\,2\,)\,\)を通る」
から、（\(\,y\,\)切片が\(\,2\,\)）
　\(\hspace{10pt}\,\underline{　y=3x+2　}\,\)

点\(\,(\,0\,,\,2\,)\,\)を\(\,y=3x+b\,\)に代入しても同じです。

問５
連立方程式を解きます。

　　\( \begin{cases}
\hspace{4pt} 2x+y=11\\
\hspace{4pt} y=3x+11
\end{cases}\)

加減法でも良いですが、
代入法の方が早いでしょう。

下の式の\(\,y\,\)の右辺を上の式の\(\,y\,\)に代入して、
　\(\begin{eqnarray}\displaystyle
2x+(3x+1)&=&11\\
2x+3x&=&11-1\\
5x&=&10\\
x&=&2
\end{eqnarray}\)

このとき、
　\(\begin{eqnarray}\displaystyle
y&=&3(2)+1\\
&=&6+1\\
&=&7
\end{eqnarray}\)

上の式に\(\,x\,\)の値を代入しても同じです。

答え　\(\,\underline{　x=2\,,\,y=7　}\,\)

問６
おうぎ形の弧の長さを求めます。

　半径\(\,9\,\mathrm{cm}\,\)、中心角\(\,60^{\circ}\,\)

公式として求めても良いですが、
比例計算で良いです。

半径\(\,r\,\)の円周は\(\,2\,\pi\,r\,\)、
これは\(\,360^{\circ}\,\)のときなので、

「中心角\(\,360^{\circ}\,\)のとき\(\,2\,\pi\times (9)\,\)、
中心角\(\,60^{\circ}\,\)のときの弧の長さは\(\,x\,\)」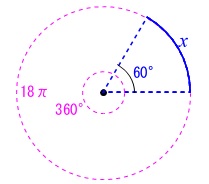
これを比例式にして
　\(\begin{eqnarray}\displaystyle
360:18\,\pi&=&60:x\\
360\,x&=&18\,\pi\times 60\\
x&=&18\,\pi\times \frac{60}{360}\\
&=&\,\underline{　3\,\pi　}(\mathrm{cm})\,
\end{eqnarray}\)

公式のように比例計算して、
　\(\begin{eqnarray}\displaystyle
18\,\pi\times \frac{60}{360}&=&x\\
x&=&3\,\pi
\end{eqnarray}\)
で良いですよ。

標準問題\(\color{black}{\fbox{　1　}}\)はここまでです。

学校裁量問題の第１問（標準問題の第２問）の解説

ここからは学校裁量問題と標準問題は共通となります。

学校裁量問題の\(\color{black}{\fbox{　1　}}\)、
標準問題の\(\color{black}{\fbox{　2　}}\)です。

問１
２次方程式を解きます。

　\(\hspace{10pt}x^2+3x-1=0\)

因数分解できないので解の公式を利用しましょう。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-3\pm \sqrt{3^2-4\cdot (-1)}}{2}\\
&=&\frac{-3\pm \sqrt{9+4}}{1}\\
&=&\underline{　\frac{-3\pm \sqrt{13}}{2}　}
\end{eqnarray}\)

問２
確率の問題です。

基本通り樹形図で良いです。

ここでは表にしますが、
樹形図の方が早いですよ。
表が\(\,○\,\)、裏が\(\,×\,\)としておきます。
　\(\begin{array}{|c|c|c|c|} \hline
100 & 50 & 10 & 合計 \\ \hline
○ & ○ & ○ & \color{red}{160} \\ \hline
○ & ○ & × & \color{red}{150} \\ \hline
○ & × & ○ & \color{red}{110} \\ \hline
○ & × & × & \color{red}{100} \\ \hline
× & ○ & ○ & \color{red}{60} \\ \hline
× & ○ & × & 50 \\ \hline
× & × & ○ & 10 \\ \hline
× & × & × & 0 \\ \hline
\end{array}\)

出かたは全部で\(\color{black}{\fbox{　8　}}\)通り、
合計金額が\(\,60\,\)円以上になる出かたは\(\color{black}{\fbox{　5　}}\)通り、
求める確率は
　\(\hspace{4pt}\displaystyle \color{black}{\fbox{\(　\frac{5}{8}　\)}}\)

問３
相対度数を求めます。

相対度数は、
　「階級の度数を度数合計で割った小数値」
です。

最も度数が多いのは
　\(\,210\,\)以上\(\,230\,\)未満の階級で\(\,\color{red}{20}\,\)
度数合計は\(\,\color{blue}{80}\,\)なので

　\(\hspace{4pt}\displaystyle \frac{\color{red}{20}}{\color{blue}{80}}=\underline{　0.25　}\)

相対度数は小数で表しますが、
割り切れないときは度数の最も多い階級で調整します。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

問４
作図です。

点\(\,\mathrm{B}\,\)と点\(\,\mathrm{P}\,\)が重なるように折り目つけます。

折り目をつける時点では、
　点\(\,\mathrm{A}\,\)と点\(\,\mathrm{C}\,\)は関係ありません。

点\(\,\mathrm{B}\,\)と点\(\,\mathrm{D}\,\)を重ねるには、
線分\(\,\mathrm{BD}\,\)の垂直二等分線を描きます。

その垂直二等分線と線分\(\,\mathrm{AB\,,\,BC}\,\)との交点が\(\,\mathrm{P\,,\,Q}\,\)です。
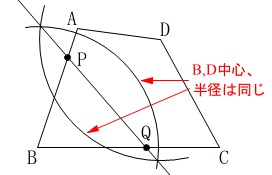作図で使う手法はだいたいですが限られていますので、
覚えておいて何を使えば良いかを思い出しながら取り組むと良いです。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

学校裁量問題\(\color{black}{\fbox{　1　}}\)、標準問題\(\color{black}{\fbox{　2　}}\)はここまでです。

学校裁量問題の第２問（標準問題の第３問）の解説

学校裁量問題の\(\color{black}{\fbox{　2　}}\)、標準問題の\(\color{black}{\fbox{　3　}}\)になります。

規則性と文字式の利用ですが、
それほど難しい問題ではないので簡単に済ませます。

問１
ストローの本数を数えていきましょう。

五角形を２個つくるのに必要なストローの本数は、
\(\,1\,\)本は重なるので、
\(\color{black}{\fbox{　9　}}\)本です。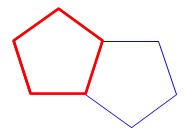五角形を\(\,3\,\)個つくるには、
さらに\(\,4\,\)本増えて、
\(\color{black}{\fbox{　13　}}\)本です。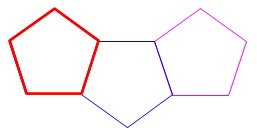五角形を１個増やすごとに、
\(\color{black}{\fbox{　\(\,\color{red}{4}\,\)　}}\)本のストローを追加することになります。

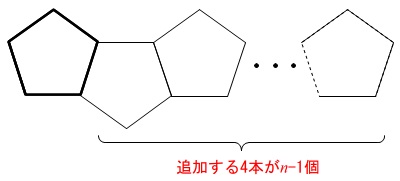
\(\,n\,\)個の五角形をつくるには、
最初の五角形に４本のストローを、
\(\color{black}{\fbox{　\(\,\color{blue}{n-1}\,\)　}}\)個増やすことになるので、
必要なストローの本数の式は
　\(\hspace{10pt}5+\color{black}{\fbox{\(\,\color{red}{4}\,\)}}(\,\color{black}{\fbox{　\(\,\color{blue}{n-1}\,\)　}}\,)\)
文字式を整理すると、
　\(\hspace{10pt}4n+1\)
となりますがここでは必要ありません。

問２
今度は正六角形が２つつながった形です。
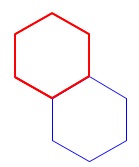問１と同じように考えれば良いので、
少し数え上げていきましょう。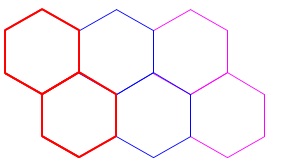最初の正六角形２つの図形のストローは、
正六角形に\(\,5\,\)本加わり\(\,\color{red}{11}\,\)本、
それが２つ重なると\(\,\color{blue}{8}\,\)本増えて\(\,19\,\)本、
３つ重なるとさらに\(\,\color{blue}{8}\,\)本増えて\(\,27\,\)本、
と増えていきます。

問題には図や表を用いて良いと書いてあるので、
問題の図を利用すると書きやすいです。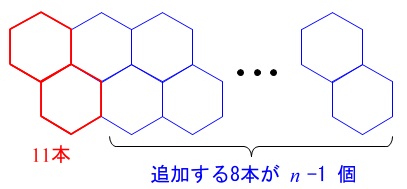
問題の図４の図形を\(\,n\,\)個つくるとき、
最初の\(\,11\,\)本に\(\,8\,\)本のストローを
\(\,(n-1)\,\)回加えることになるので
必要なストローの本数は
　\(\hspace{10pt}11+8\,(\,n-1\,)\\
=8n+3\)

問１の文字式が意味を表す形、
　\(\hspace{10pt}5+4\,(\,n-1\,)\)
で終わっているので、
　\(\hspace{10pt}11+8\,(\,n-1\,)\)
でも問題はありません。

間違えやすい別の考え方

また、別の考え方として正六角形が\(\,n\,\)個並んだ下に、
正六角形が\(\,1\,\)辺を重ねて並べてあるとみると、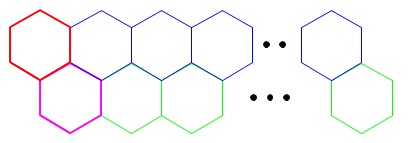上段の並びで必要なストローの本数は
　\(\hspace{10pt}6+5(n-1)\\
=5n+1\)
下段に必要なストローの本数は
　\(\hspace{10pt}4+3(n-1)\\
=3n+1\)
なので必要なストローの本数は
　\(\hspace{10pt}8n+2\)

とすると間違いです。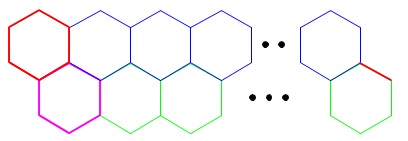最後の\(\,\color{red}{1}\,\)本が加えられていません。

必要な本数は
　\(\hspace{10pt}8n+2\color{red}{+1}\\
=8n+3\)
となります。

さらに、総本数から重なった辺の数を引く考え方をして見ると、

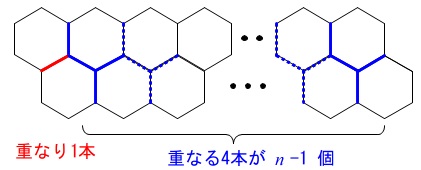
正六角形が\(\,2\,n\,\)個の辺の数は
　\(\hspace{10pt}6\times 2\,n\\
=12\,n\)
重なる辺の数は最初\(\,1\,\)本で
後は\(\,4\,\)本ずつ\(\,n-1\,\)回重なるので、
　\(\hspace{10pt}1+4\,(\,n-1\,)\\
=4\,n-3\)
辺の総数から重なる辺の数を引けば良いので、
　\(\hspace{10pt}12\,n-(4\,n-3)\\
=8\,n+3\)

これは正しいです。
総数から部分を引くというのはよく利用します。

しかし、問１を参考に考えるなら図４を利用した方が早いでしょう。

学校裁量問題の第３問（標準問題の第４問）の解説

関数と座標上の線分の和の最短距離の問題です。

学校裁量問題の\(\color{black}{\fbox{　3　}}\)、標準問題の\(\color{black}{\fbox{　4　}}\)になります。

関数は
　\(\hspace{4pt}y=ax^2　･･･①\)
ですが\(\,a\,\)は正の定数となっているので、
下に凸（上に開いている）原点を頂点とする放物線です。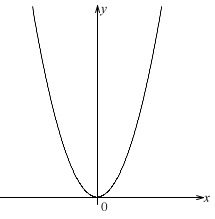
問１
\(\,a=4\,\)のとき、
\(\,①\,\)のグラフと\(\,x\,\)軸ついて対称なグラフを表す関数を求めます。

比例定数\(\,a=4\,\)と具体的に決まっているので
\(\,①\,\)の関数も固定されます。
　\(\hspace{4pt}y=4\,x^2\)
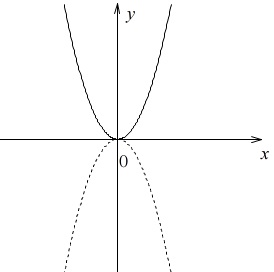\(\,x\,\)軸について対称な関数は
比例定数が負の値になるだけです。

　\(\hspace{10pt}\underline{　y=-4\,x^2　}\)

関数の問題は（できるだけ）グラフで見ていくとわかりやすいです。

問２
今度は比例定数\(\,a\,\)を求めます。

　\(\,x\,\)の変域が\(\,-2≦x≦3\,\)
のとき
　\(\,y\,\)の変域が\(\,0≦y≦18\,\)

軸は\(\,x=0\,\)なので、
軸から遠い\(\,x=3\,\)のとき最大で、
\(\,y=18\,\)となります。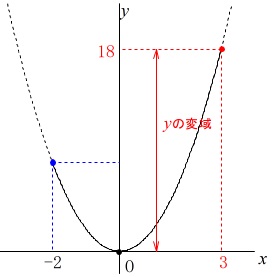
　\(\begin{eqnarray}\displaystyle
18&=&a\times (3)^2\\
a&=&\underline{　2　}
\end{eqnarray}\)

「比例定数」は比例、反比例も同じ言葉を使うので注意しておきましょう。

問３
条件を満たす座標を求めます。

\(\,①\,\)のグラフ上に２点\(\,\mathrm{A,B}\,\)、
\(\,y\,\)軸上に点\(\,\mathrm{C}\,\)をとり、
線分\(\,\mathrm{AC}\,\)と線分\(\,\mathrm{BC}\,\)の長さの和が最も小さくなるときの、
点\(\,\mathrm{C}\,\)の座標です。

問題文を読んでいても先に進めません。
条件をグラフで示していきましょう。

条件
　比例定数は\(\,a=1\,\)
　点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,2\,\)
　点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,3\,\)
　点\(\,\mathrm{C}\,\)は\(\,y\,\)軸上の点

関数は\(\,y=x^2\,\)なので、
　点\(\,\mathrm{A}\,\)の座標は\(\,(\,2\,,\,4\,)\)
　点\(\,\mathrm{B}\,\)の座標は\(\,(\,3\,,\,9\,)\)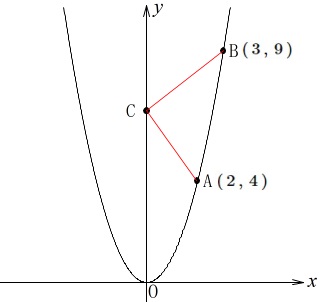図形問題で良くありますが、
最短になるのは３点が直線上に並ぶときです。

説明すると長くなるので『覚え太郎』で確認しておいてください。

この場合\(\,\mathrm{A,B,C}\,\)は直線上に並べることはできませんので、
\(\,\mathrm{A}\,\)か\(\,\mathrm{B}\,\)を\(\,y\,\)軸で対称移動させれば良いだけです。

\(\,\mathrm{A}\,\)を\(\,y\,\)軸で対称移動させると
　\(\hspace{4pt}\mathrm{A’}\,(\,-2\,,\,4\,)\)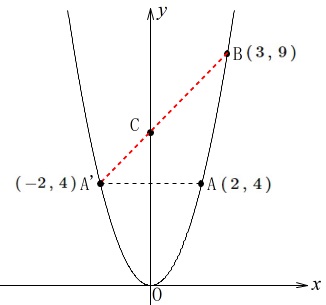このとき、
点\(\,\mathrm{A’\,,\,C\,,\,B}\,\)が直線上に並べば最短になるので、
直線\(\,\mathrm{A’B}\,\)の\(\,y\,\)切片となる点\(\,\mathrm{C}\,\)の座標を求めれば良いのです。

２点
　\(\hspace{4pt}\mathrm{A’}\,(\,-2\,,\,4\,)\)
　\(\hspace{4pt}\mathrm{B}\,(\,3\,,\,9\,)\)
を通る直線は傾きが
　\(\hspace{4pt}\displaystyle \frac{9-4}{3-(-2)}=1\)
なので\(\,y=x+b\,\)とおけて
　\(\hspace{4pt}\mathrm{B}\,(\,3\,,\,9\,)\)
を通ることから（\(\,\mathrm{A’}\,\)でも良いです。）
　\(\begin{eqnarray}\displaystyle
9&=&3+b\\
b&=&6
\end{eqnarray}\)
よって直線\(\,\mathrm{A’B}\,\)の式は
　\(\hspace{10pt}y=x+6\)
なので点\(\,\mathrm{C}\,\)の座標は
　\(\hspace{10pt}\underline{　\mathrm{C}\,(\,0\,,\,6\,)　}\)

ここでは点\(\,\mathrm{A}\,\)を対称移動しましたが、
点\(\,\mathrm{B}\,\)を対称移動しても結果は同じです。

方法は同じなので自分で確認してみてください。

学校裁量問題の第４問（標準問題の第５問）の解説

学校裁量問題の\(\color{black}{\fbox{　4　}}\)、標準問題の\(\color{black}{\fbox{　5　}}\)になります。

除外された単元が大きく影響し、
楽な問題になっているので簡単に済ませます。

台形と対角線があります。

　台形ＡＢＣＤがあり、
　\(\,\mathrm{AD}\,\)　∥　\(\,\mathrm{BC}\,\)
　\(\,\mathrm{AC\,,\,BD}\,\)の交点を\(\,\mathrm{E}\,\)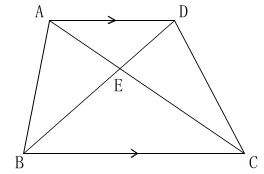
問１
角度の大きさを求めます。

　\(\,\mathrm{ＣＤ＝ＣＥ}\,\)
　\(\,\mathrm{∠ＡＣＤ=30^{\circ}}\,\)
のときの\(\,\mathrm{∠ＢＥＣ}\,\)の大きさです。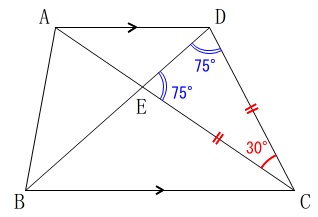二等辺三角形の頂角が\(\,30^{\circ}\,\)で、
底角は等しいので
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ＣＤＥ}&=&\mathrm{∠ＣＥＤ}\\
&=&\frac{180^{\circ}-30^{\circ}}{2}\\
&=&75^{\circ}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BEC}&=&180^{\circ}-75^{\circ}\\
&=&\underline{　105^{\circ}　}
\end{eqnarray}\)

問２
証明問題です。

点\(\,\mathrm{F}\,\)を通り対角線\(\,\mathrm{AC}\,\)に平行な直線を引き、
辺\(\,\mathrm{AB,BC}\,\)との交点をそれぞれ\(\,\mathrm{G,H}\,\)とします。

条件
　点\(\,\mathrm{F}\,\)は線分\(\,\mathrm{BE}\,\)上の点
　\(\,\mathrm{BF=DE}\,\)
　\(\,\mathrm{AC}\,\)　∥　\(\,\mathrm{GH}\,\)
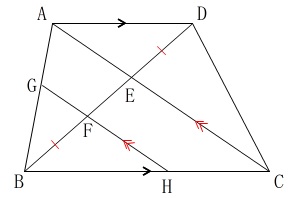このとき、
　\(\hspace{10pt}\mathrm{AD=HB}\)
を証明します。

長さが等しいことの証明ですが、
　\(\hspace{4pt}\mathrm{△ADE　≡　△HBF}\)
を言えば対応する辺は等しいので証明したことになります。

図形の証明は図の中で終わらせておくことが基本ですね。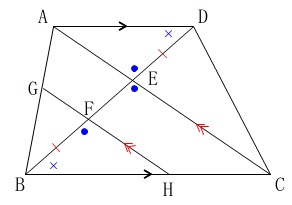
（証明）
　\(\,\mathrm{△ADE}\,\)と\(\,\mathrm{△HBF}\,\)において
仮定から
　\(\,\mathrm{DE=BF　･･･①}\,\)
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)なので錯角は等しく
　\(\,\mathrm{∠ADE=∠HBF}　･･･②\)
また対頂角は等しいことから
　\(\,\mathrm{∠AED=∠CEB}　･･･③\)
また\(\,\mathrm{AC}\,\)∥\(\,\mathrm{GH}\,\)なので同位角は等しく
　\(\,\mathrm{∠HFB=∠CEB}　･･･④\)
\(\,③④\,\)から
　\(\,\mathrm{∠AED=∠HFB}　･･･⑤\)
①②⑤より
　１組の辺とその両端の角がそれぞれ等しい
ので
　\(\,\mathrm{△ADE\,≡\,△HBF}\,\)
合同な図形の対応する辺は等しいので
　\(\hspace{4pt}\mathrm{AD=HB}\)
（終わり）

証明の書き方は合同条件がそろっていれば、
順番は違っていても構いません。

標準問題は以上です。

次は学校裁量問題のみの出題内容になります。

学校裁量問題の第５問

\(\color{black}{\fbox{　5　}}\)
学校裁量問題です。

問１
おうぎ形をすべらないように直線上で回転させます。
よく見かける問題ではあるので答えはすぐに出てきますが、
なれていない人は手を動かさないと迷うかもしれません。

(1)
半径\(\,2\,\)、中心角\(\,120°\,\)のおうぎ形です。

手順は問題の通り。

操作\(\color{black}{\fbox{1}}\)の間は、
半径\(\,\mathrm{PQ=2}\,\)、中心を\(\,\mathrm{Q}\,\)とする四分円を描きます。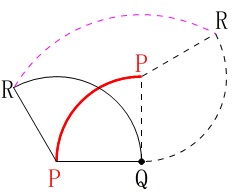
操作\(\color{black}{\fbox{2}}\)の間は、
弧\(\,\mathrm{QR}\,\)から\(\,\mathrm{P}\,\)までの距離は半径で一定なので線分になります。
操作3の間は、
半径\(\,\mathrm{RP=2}\,\)、中心を\(\,\mathrm{R}\,\)とする四分円を描きます。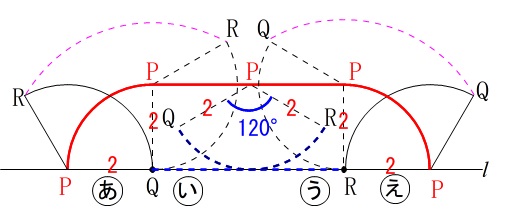
よって求める点\(\,\mathrm{P}\,\)の描く線の長さは、
半径\(\,2\,\)の
　半円（四分円２つ分）
と
　中心角\(\,120°\,\)のおうぎ形
の弧の長さの和になるので
　\(\hspace{10pt}\displaystyle 2\,\pi\,(2)\times \frac{1}{2}+2\,\pi\,(2)\times \frac{120}{360}\\
\displaystyle =2\,\pi+\frac{4}{3}\,\pi\\
\displaystyle =\underline{　\frac{10}{3}\,\pi　}　(\mathrm{cm})\)

半径\(\,2\,\)、中心角\(\,300°\,\)のおうぎ形の弧の長さとして
　\(\hspace{10pt}\displaystyle 2\,\pi\,(2)\times \frac{300}{360}\\
\displaystyle =4\,\pi\,\times \frac{5}{6}\\
\displaystyle =\frac{10}{3}\,\pi　(\mathrm{cm})\)

としても良いです。

問題は「えがく線の長さを求めなさい。」となっていますが、
「えがく曲線の長さを求めなさい。」
となっていても同じですので注意しておきましょう。
※
曲線というのは直線を含みます。

(2)
今度は正三角形に弧がついた図形を転がします。

図形\(\,\mathrm{F}\,\)は正三角形が、
正三角形の１辺と同じ半径の弧で囲まれた図形です。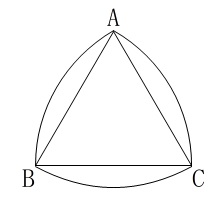
面積を求めるわけではないので、
(1)を参考にすれば答えはすぐに分かるでしょう。

操作\(\color{black}{\fbox{1}}\)は点\(\,\mathrm{B}\,\)を中心に\(\,60°\,\)回転するだけです。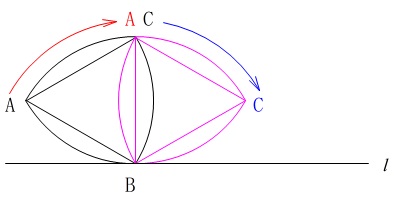
操作\(\color{black}{\fbox{2}}\)は弧\(\,\mathrm{BC}\,\)が直線\(\,l\,\)上をすべらずに転がります。
(1)と同じように点\(\,\mathrm{A}\,\)は弧\(\,\mathrm{BC}\,\)の長さだけ\(\,l\,\)に平行に移動します。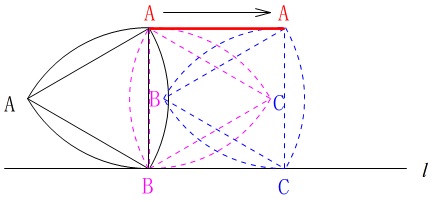
操作\(\color{black}{\fbox{3}}\)\(\color{black}{\fbox{4}}\)\(\color{black}{\fbox{5}}\)\(\color{black}{\fbox{6}}\)は、
操作\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)を\(\,2\,\)回繰り返すだけです。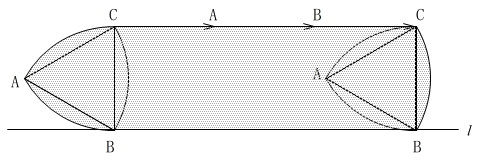

答え　\(\,\underline{　ウ　}\,\)

問２
動点問題を含む立体の問題です。

立方体は１辺が\(\,a\,\)です。
※
単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。

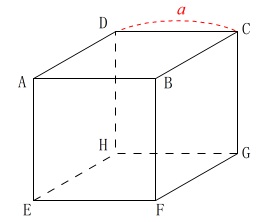
(1)
立方体の\(\,1\,\)辺が\(\,a=4\,\)の場合です。

立方体を３点\(\,\mathrm{A\,,\,C\,,\,G}\,\)を通る平面で切ったとき、
頂点\(\,\mathrm{F}\,\)を含む立体の体積を求めます。

３点\(\,\mathrm{A\,,\,C\,,\,G}\,\)を通る平面は点\(\,\mathrm{E}\,\)を含むので、
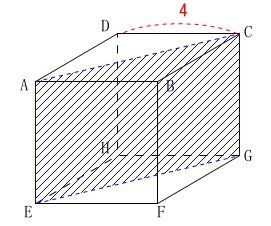立方体を半分に切ったときの体積を求めれば良いだけです。

求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{2}\times 4^3\\
&=&\underline{　32　}　(\mathrm{cm^3})
\end{eqnarray}\)

(2)
今度は３点\(\,\mathrm{B\,,\,E\,,\,G}\,\)を通る平面で切ります。
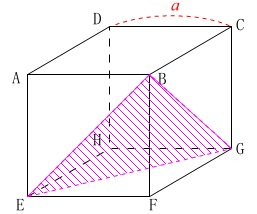頂点\(\,\mathrm{F}\,\)をふくむ立体は三角錐なので、
立方体から見ればすぐに答えが出ます。

答え　\(\displaystyle \underline{　\frac{1}{6}　}\)　倍

体積を求めるとすれば１辺を\(\,a\,\)として計算しても同じですが、
長さに関係なく成り立つ関係なので、
(1)の\(\,a=4\,\)の場合で計算しても良いですよ。

点\(\,\mathrm{F}\,\)を含む三角錐の体積\(\,V’\,\)は、
底面積が
　\(\hspace{4pt}\displaystyle \frac{1}{2}\times 4^2=8\)
高さが\(\,4\,\)の三角錐なので
　\(\begin{eqnarray}\displaystyle
V’&=&\frac{1}{3}\times 8\times 4\\
&=&\frac{32}{3}
\end{eqnarray}\)

立方体の体積は
　\(\hspace{4pt}4^3=64\)
なので
　\(\hspace{10pt}\displaystyle \frac{32}{3}\div 64\\
\displaystyle =\frac{32}{3}\times \frac{1}{64}\\
\displaystyle =\underline{　\frac{1}{6}　}　倍\)

立体の切り口（断面）が分かればすぐに答えが出る問題です。

(3)
動点問題です。

ただ、動点は平面上を動くので、
見方を変えれば立体の問題ではありません。

条件が長いのでまとめておきましょう。

条件
　\(\,a=10\,\)（立方体の１辺）
　点\(\,\mathrm{P\,,\,Q}\,\)は四角形\(\,\mathrm{ABCD}\,\)の辺上を動く。
　点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)の速さで\(\,\mathrm{A}\,\)を出発し、
　\(\,\mathrm{A\,\rightarrow B\,\rightarrow C}\,\)と移動する。
　点\(\,\mathrm{Q}\,\)は毎秒\(\,2\,\)の速さで\(\,\mathrm{B}\,\)を出発し、
　\(\,\mathrm{B\,\rightarrow C\,\rightarrow D\,\rightarrow A\,\rightarrow B}\,\)と移動する。
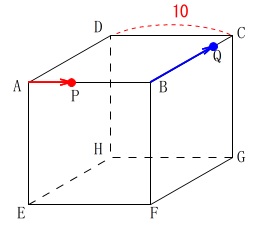２直線\(\,\mathrm{PQ,EG}\,\)が同じ平面にあるのは、
出発してから何秒後かを求めます。

直線\(\,\mathrm{EG}\,\)と直線\(\,\mathrm{PQ}\,\)が同じ平面にあるのは、
直線\(\,\mathrm{EG}\,\)と直線\(\,\mathrm{PQ}\,\)が平行なときなので、
直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{PQ}\,\)が平行でもあります。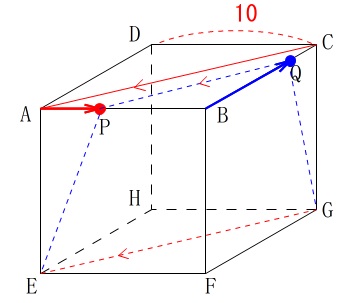
このことから立方体ではなく、
正方形\(\,\mathrm{ABCD}\,\)を抜き出し平面で考えれば良いのです。

直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{PQ}\,\)が平行になるのは、
\(\,\mathrm{P,Q}\,\)の動ける範囲から２つの場合が考えられます。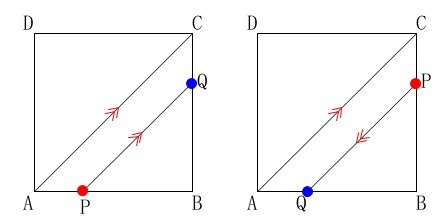
点\(\,\mathrm{P}\,\)が辺\(\,\mathrm{AB}\,\)上にあるとき、
点\(\,\mathrm{Q}\,\)は辺\(\,\mathrm{BC}\,\)上にないと平行になりません。

点\(\,\mathrm{P}\,\)が\(\,\mathrm{BC}\,\)上にあるとき、
点\(\,\mathrm{Q}\,\)は辺\(\,\mathrm{AB}\,\)上にないと平行になりません。　

これらの関係を文字を使って方程式にしましょう。

出発してから\(\,x\,\)秒間での移動は
　\(\,\mathrm{P}\,\)が\(\,\color{red}{x}\,\)、\(\,\mathrm{Q}\,\)は\(\,\color{blue}{2x}\,\)

点\(\,\mathrm{P}\,\)が\(\,\mathrm{AB}\,\)上、
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{BC}\,\)上にあるのは
　\(0≦x≦5\)
のときで
　\(\,\mathrm{AP}=\color{red}{x}\,\)
　\(\,\mathrm{PB}=10-\color{red}{x}\,\)
　\(\,\mathrm{BQ}=\color{blue}{2x}\,\)
　\(\,\mathrm{CQ}=10-\color{blue}{2x}\,\)
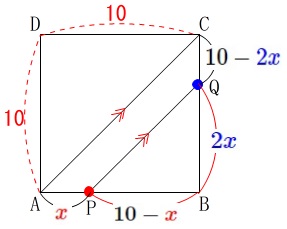直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{PQ}\,\)が平行になるのは
　\(\,\mathrm{AP=CQ}\,\)　または　\(\,\mathrm{PB=BQ}\,\)
となるときで、
　\(\begin{eqnarray}\displaystyle
\mathrm{AP}&=&\mathrm{CQ}\\
x&=&10-2x\\
3x&=&10\\
x&=&\frac{10}{3}
\end{eqnarray}\)
　
これは\(\,0≦x≦5\,\)にあるので適しています。

次に、
点\(\,\mathrm{P}\,\)が\(\,\mathrm{BC}\,\)上、
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{AB}\,\)にあるのは
\(\,\mathrm{B}\,\)が\(\,\mathrm{A}\,\)をこえてからだから
　\(15≦x≦20\)
のときで直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{QP}\,\)が平行になるのは
　\(\,\mathrm{AQ=CP}\,\)　または　\(\,\mathrm{QB=PB}\,\)
のときです。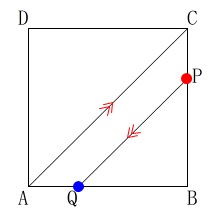
このとき
　\(\,\mathrm{AB+BC=20}\,\)
なので
　\(\,\mathrm{CP}=20-\color{red}{x}\,\)
または
　\(\,\mathrm{PB}=\color{red}{x}-10\,\)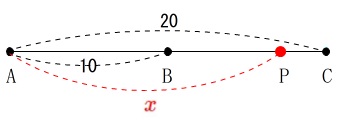折り返しや曲がり角があるときは、
直線だと考えると分かり易いですよ。

同じように、
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{B}\,\)から\(\,\mathrm{C\,,\,D\,,\,A}\,\)と移動すると、
\(\,\mathrm{A}\,\)までで\(\,30\,\)なので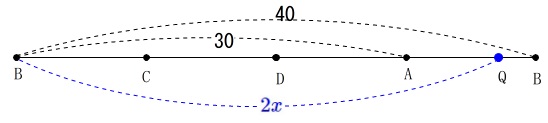
　\(\,\mathrm{AQ}=\color{blue}{2x}-30\,\)
または
　\(\,\mathrm{BQ}=40-\color{blue}{2x}\,\)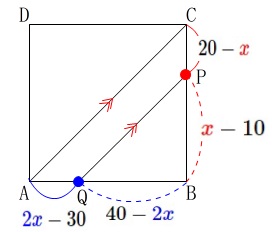直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{QP}\,\)が平行なときなので
　\(\mathrm{AQ=CP}\)　または　\(\mathrm{BQ=BP}\)
（どっちでも同じですよ。）