高知県公立高校入試2020年(令和2年度)A日程の数学の問題と解説

2020年(令和2年度)に高知県で実施されたA日程公立高校入試の数学の問題と解説です。
ここ数年の構成と同じで大問6まであり50点満点です。
応用も多少ありますが基本中心なので高得点（会員は満点）が狙えます。
ただし、高知県は1問の配点比率が大きいのでミスには気をつけておきましょう。

高知県公立高校入試2020年(令和2年度)A日程の数学の問題

問題は高知県が公開してくれています。

⇒　令和2年度高知県公立高校入試A日程の数学の問題

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであり\(\,50\,\)点満点です。

高知県公立高校入試2020年(令和2年度)A日程の数学の解説

クセのある応用問題はないので、
方針は示しますが解説はそれほど詳しくしません。

第１問

\(\color{black}{\fbox{1}}\)

小問集合で(1)から(8)まであります。

(1)\(\,4\,\)題の計算問題です。

①
　\(\hspace{10pt}-5-4+7\\
=-9+7\\
=\underline{　-2　}\)

暗算しても良いですが見直しはしましょう。
\(\,4\,\)％の配点があるのです。

②
　\(\hspace{10pt}\displaystyle \frac{2x+y}{4}-\frac{x-2y}{6}\\
\displaystyle =\frac{3(2x+y)-2(x-2y)}{12}\\
\displaystyle =\frac{6x+3y-2x+4y}{12}\\
\displaystyle =\underline{　\frac{4x+7y}{12}　}\)

分母を1つに分子の計算に集中です。
\(\,3\,\)行目は暗算しない方がミスは減ります。

③
　\(\hspace{10pt}24a^2b^2\div (-6b^3)\div 2ab\\
\displaystyle =-\frac{24a^2b^2}{6b^3\times 2ab}\\
\displaystyle =\underline{　-\frac{2a}{b^2}　}\)

文字式でも数値計算でも同じです。
符号に気をつけて、
分母にまわる部分と分子に残る部分をしっかり分ければ約分です。

④
　\(\hspace{10pt}\displaystyle \sqrt{75}-\frac{9}{\sqrt{3}}\\
\displaystyle =5\sqrt{3}-\frac{9\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\\
\displaystyle =5\sqrt{3}-\frac{9\sqrt{3}}{3}\\
\displaystyle =5\sqrt{3}-3\sqrt{3}\\
=\underline{　2\sqrt{3}　}\)

\(\,2,3\,\)行目の分母の有理化は暗算できるでしょうが、
素因数分解は必ずやっておきましょう。

(2)
長方形があって、
　周の長さが\(\,a\,\)
　縦の長さが\(\,\color{red}{5}\,\)
　横の長さが\(\,\color{blue}{b}\,\)
（単位は\(\,\mathrm{cm}\,\)です。）

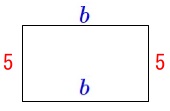
このとき\(\,b\,\)を\(\,a\,\)の式で表します。

　\(\begin{eqnarray}\displaystyle
2\times (5+b)&=&a\\
10+2b&=&a\\
2b&=&a-10\\
b&=&\underline{　\frac{a-10}{2}　}
\end{eqnarray}\)

関係式を表すだけなので単位は必要ありません。

「長方形」という文字を見て図を書かない人は、余程満点の自信があるか、解く気がない人です。
私は満点とる確信がないので図を書いて確認します。
「図を書くほどの問題ではない。」という偉い人は書かなくて良いです。
ただ、手を動かすクセのない人は高校数学で撃沈してください。

(4)
食塩水を混ぜる問題です。
　\(\,4\,\)％の食塩水を\(\,x\,\)
　\(\,9\,\)％の食塩水を\(\,y\,\)
混ぜて
　\(\,6\,\)％の食塩水\(\,600\,\)
をつくります。
（食塩水の単位は\(\,\mathrm{g}\,\)ですが計算途中では省略します。）

「食塩水」の関係は
　\(\hspace{4pt}x+y=600　･･･①\)
「食塩」の関係は
　\(\hspace{4pt}\displaystyle 4\times \frac{x}{100}+9\times \frac{y}{100}=6\times \frac{600}{100}　･･･②\)
です。
\(\,①②\,\)を連立して\(\,x\,\)を求めます。

⇒　連立方程式(食塩水の濃度と食塩水を混ぜる文章問題の立式方法と解き方)

食塩を追う比例式が分からない人は参考にしてください。

\(\,①②\,\)から（連立方程式は解けるとして省略します。）
　\(\hspace{10pt}x=\underline{　360　\mathrm{g}}\)

（\(\,y\,\)は求めなくても良い問題です。）

食塩水は全体で\(\,600\,\)になることから
　\(\,4\,\)％の食塩水を\(\,x\,\)
　\(\,9\,\)％の食塩水を\(\,600-x\,\)
混ぜて
　\(\,6\,\)％の食塩水\(\,600\,\)
をつくる、とおけば
　\(\begin{eqnarray}\displaystyle
4\times \frac{x}{100}+9\times \frac{600-x}{100}&=&6\times \frac{600}{100}\\
4x+9(600-x)&=&6\times 600\\
4x+5400-9x&=&3600\\
-5x&=&-1800\\
x&=&360
\end{eqnarray}\)

連立方程式ではなく\(\,1\,\)次方程式の問題になります。
もちろん、どちらでも構いません。

いずれにしても食塩水を混ぜる問題は、
「食塩水」の量と「食塩」の量で方程式を立てることを考えると分かり易いです。
（水を加えたりするときも同じです。）

何の話？と思われた人は思い出しておいてください。
「溶液」は「溶媒」と「溶質」が混じってできます。
食塩水でいうと
　食塩水が溶液
　水が溶媒
　食塩が溶質
ですが、溶液と溶質で方程式を立てると考えやすいということです。

(4)
　\(\hspace{4pt}2x^2+7x+1=0\)
を解きます。
因数分解できないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-7\pm \sqrt{7^2-4(2)(1)}}{2\times 2}\\
&=&\frac{-7\pm \sqrt{49-8}}{4}\\
&=&\underline{　\frac{-7\pm \sqrt{41}}{4}　}
\end{eqnarray}\)

(5)
\(\,y=-x^2\,\)において、
　\(-2\,≦\,x\,≦\,3\,\)
の\(\,y\,\)の変域です。
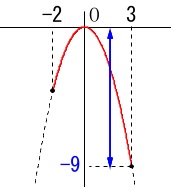\(\,y\,\)の変域は
　\(\hspace{4pt}-9\,≦\,y\,≦\,0\)

答え　\(\,\underline{　a=-9\,,\,b=0　}\,\)

\(\,y\,\)変域（値域）は区間の最小値と最大値が関係するだけで、
\(\,x=-2\,\)のときの\(\,y\,\)の値は関係ありません。

(6)
\(\,1\,\)辺\(\,12\,\)の立方体に接している球なので、
球の半径は\(\,6\,\)です。
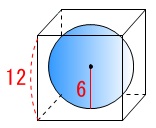求める球の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{4}{3}\,\pi\times (6)^3\\
&=&\underline{　288\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

この問題はもっと発展させておきたい問題ですが通過します。

(7)
ヒストグラムを読み取れば分かりますが、
変形した度数分布表にしておきます。
　\(\begin{array}{|c|c|c|c|} \hline
階級 & 階級値 & 度数 & 累積度数 \\ \hline
\,0\,～\,1\, & 0.5 & 6 & \\ \hline
1\,～\,2 & \color{blue}{1.5} & \color{blue}{8} & 14 \\ \hline
2\,～\,3 & \color{red}{2.5} & 7 & \color{red}{21} \\ \hline
3\,～\,4 & 3.5 & 5 & 26 \\ \hline
4\,～\,5 & 4.5 & 5 & 31 \\ \hline
5\,～\,6 & 5.5 & 3 & 34 \\ \hline
6\,～\,7 & 6.5 & 3 & 37 \\ \hline
7\,～\,8 & 7.5 & 2 & 39 \\ \hline
8\,～\,9 & 8.5 & 1 & 40 \\ \hline
\end{array}\)

平均値は\(\,3.3\,\)なので
　\(\hspace{4pt}a=3.3\,\)
中央値は\(\,40\,\)人のデータなので
　\(\hspace{4pt}b=\color{red}{2.5}\)
最頻値は度数が\(\,8\,\)の階級値になるので
　\(\hspace{4pt}c=\color{blue}{1.5}\)

答え　\(\,\underline{　c\,＜\,b\,＜\,a　}\,\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値は少なくとも小学生から高校生までは使います。

(8)
\(\,\mathrm{A}\,\)を通り\(\,\mathrm{∠B}\,\)の二等分線に垂直な線分が\(\,\mathrm{AP}\,\)です。

　\(\,\color{red}{①}\,\)\(\,\mathrm{∠B}\,\)の二等分線をかきます。
　\(\,\color{blue}{②}\,\)\(\,\mathrm{A}\,\)から\(\,\color{red}{①}\,\)で描いた角の二等分線に垂線を引きます。
その交点が\(\,\mathrm{P}\,\)です。
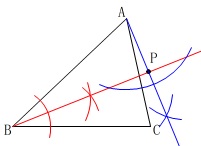数学では通常、距離は最短距離を意味します。
1つの点から直線までの距離は、
垂直になるとき最短になります。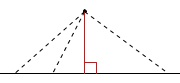

作図については使う方法は限られます。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

問題の意味していることをしっかり読み取りましょう。

第２問

\(\color{black}{\fbox{2}}\)

文字式の基本問題です。

(1)
奇数は整数で1つの奇数の\(\,+2\,\)が次の奇数になります。

最も小さい奇数を\(\,2n+1\,\)とすると、
4つの連続する奇数は
　\(\,2n+1\,,\,2n+3\,,\,2n+5\,,\,2n+7\,\)
になります。

答え
　\(\color{black}{\fbox{　ア　}}\)\(\,\underline{　2n+3　}\,\)
　\(\color{black}{\fbox{　イ　}}\)\(\,\underline{　2n+5　}\,\)
　\(\color{black}{\fbox{　ウ　}}\)\(\,\underline{　2n+7　}\,\)

(2)
次は連続する5つの整数です。

連続する5つの整数は\(\,n\,\)を整数として
　\(n\,,\,n+1\,,\,n+2\,,\,n+3\,,\,n+4\)
または、
　\(n-2\,,\,n-1\,,\,n\,,\,n+1\,,\,n+2\)
とおくことができます。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

求めたいの整数が最も小さい整数なので、
　\(n\,,\,n+1\,,\,n+2\,,\,n+3\,,\,n+4\)
で直接\(\,n\,\)を求めます。

　\(\hspace{10pt}n+n+1+n+2+n+3+n+4\\
=5n+10\)
よって、
　\(\begin{eqnarray}
5\,n+10&=&280\\
5\,n&=&270\\
n&=&\underline{　54　}
\end{eqnarray}\)

　\(n-2\,,\,n-1\,,\,n\,,\,n+1\,,\,n+2\)
を使った場合
　\(\hspace{10pt}n-2+n-1+n+n+1+n+2\\
=5n\)
より
　\(\begin{eqnarray}
5n&=&280\\
n&=&56
\end{eqnarray}\)
となりますが、
最も小さい整数は、
　\(\hspace{10pt}n-2=56-2=\underline{　54　}\)
なので\(\,n\,\)そのものを答えにしないように気をつけておきましょう。

(3)
\(\,280\,\)が3つの連続する偶数で表せない理由を文字式を使って説明します。

\(\,280\,\)が\(\,6\,\)の倍数でないのですぐに分かりますが、
文字式で理由を説明しなさい、ということです。

3つの連続する偶数は整数\(\,n\,\)を用いて
　\(2n\,,\,2n+2\,,\,2n+4\)
または、
　\(2n-2\,,\,2n\,,\,2n+2\)
とおけます。
整数なのでどちらでも良いです。

連続する3つの偶数を整数\(\,n\,\)を用いて
　\(2n-2\,,\,2n\,,\,2n+2\)
と表すと、3つの連続する偶数の和は
　\(\hspace{10pt}2n-2+2n+2n+2\\
=6n\)
このとき
　\(\begin{eqnarray}\displaystyle
6n&=&280\\
n&=&\frac{140}{3}
\end{eqnarray}\)
これは満たす整数\(\,n\,\)が存在しないことを意味しています。
つまり、
　\(\,280\,\)は、連続する3つの偶数の和では表すことができない。

第３問

平面図形の円と内接する三角形の問題ですが、
円周角についての角度の関係だけです。

条件
　\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)は円\(\,\mathrm{O}\,\)の周上にある。
　\(\,\mathrm{∠OBC}=∠\,x\,\)
　\(\,\mathrm{∠BAC}=∠\,y\,\)

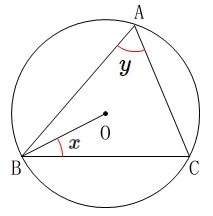
(1)\(\,∠\,y\,\)が鋭角のとき、
\(\,∠\,x+∠\,y=90^{\circ}\,\)となることの説明です。
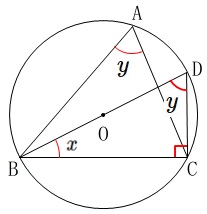\(\,\mathrm{BD}\,\)が直径なので
　\(\,\mathrm{∠BCD}=90^{\circ}\,\)
三角形の内角の和は\(\,180^{\circ}\,\)なので
　\(\,\mathrm{∠DBC+∠BDC}=90^{\circ}\,\)
同一の弧\(\,\mathrm{BC}\,\)に対する円周角は等しいので
　\(\,\mathrm{∠BAC=∠BDC}=∠\,y\,\)
よって、
　\(\,∠\,x+∠\,y=90^{\circ}\,\)

(2)
\(\,∠\,y\,\)が鈍角の場合です。
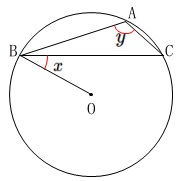(1)と同様に直径を利用することもできますが、
半径が等しいことから二等辺三角形の底角が利用できます。
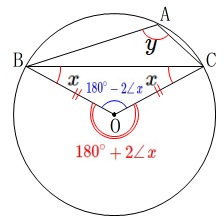半径が等しいことから\(\,\mathrm{△OBC}\,\)は二等辺三角形で
　\(\,\mathrm{∠OBC=∠OCB}=∠x\,\)
三角形の内角の和から
　\(\color{blue}{\mathrm{∠BOC}=180^{\circ}-2∠\,x}\)
なので\(\,∠\,y\,\)の中心角は
　\(\,\color{red}{180^{\circ}+2∠\,x}\,\)

中心角は円周角の\(\,2\,\)倍なので
　\(\begin{eqnarray}\displaystyle
2∠\,y&=&180^{\circ}+2∠\,x\\
∠\,y&=&90^{\circ}+∠\,x
\end{eqnarray}\)

答え　\(\,\underline{　∠\,y=90^{\circ}+∠\,x　}\,\)

(1)と同じような関係式の表し方をするなら
　\(\hspace{4pt}\underline{　∠\,y-∠\,x=90^{\circ}　}\)

また(1)と同様に直径を利用すると
　\(\hspace{4pt}\color{red}{\mathrm{∠BDC}=90^{\circ}-∠\,x}\)
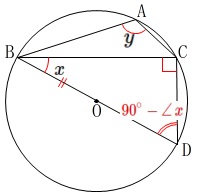内接する四角形の内対角の和は\(\,180^{\circ}\,\)なので
　\(\begin{eqnarray}
∠\,y+90^{\circ}-∠\,x&=&180^{\circ}\\
∠\,y-∠\,x&=&90^{\circ}
\end{eqnarray}\)

※
この問題では\(\,x,y\,\)は位置を表しています。
だから\(\,x\,\)の角度を\(\,∠x\,\)などと表すことになります。
角度を\(\,x,y\,\)としてくれていたら
　\(x+y=90^{\circ}\)
　\(y-x=90^{\circ}\)
とできるのですが、厳しく減点対象にしているのかどうかは分かりません。

第４問

\(\color{black}{\fbox{4}}\)

さいころを\(\,2\,\)回投げる確率です。
さいころを\(\,2\,\)回投げるのと、
さいころを2つ投げることは同じことです。

最初の状態と手順がありますので、
条件としてまとめておきます。

条件
　表裏が白と黒になっているこまが\(\,6\,\)枚
　左回りに\(\,\mathrm{A,B,C,D,E,F}\,\)の順に、
　白が上を向いておいてある。
　\(\,1\,\)回目の出た目の数だけ\(\,\mathrm{A}\,\)から左回りにうら返す。
　\(\,2\,\)回目の出た目の数だけ\(\,\mathrm{F}\,\)から右回りにうら返す。

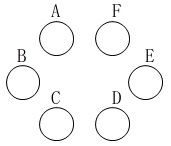
(1)
\(\,6\,\)枚がすべて黒が上を向く確率です。

さいころの出る目は\(\,6\,\)まであるので、
一度ですべて黒にすることもできますが、
\(\,2\,\)回目のさいころで白に戻されると\(\,6\,\)枚が黒にはなりません。
\(\,2\,\)度目のさいころの出る目で\(\,0\,\)はないので、
\(\,1\,\)度目の出る目は\(\,6\,\)はありません。

などと試している内に
　\(\,1\,\)回目の出る目を\(\,\color{red}{a}\,\)
　\(\,2\,\)回目に出る目を\(\,\color{blue}{b}\,\)
とすると
　\(\hspace{10pt}\color{red}{a}+\color{blue}{b}=6\)
となる確率を求めれば良いことが分かります。
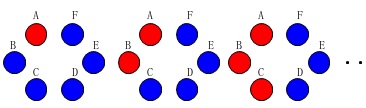言い方を変えると
　\(\,\color{red}{1}\,\)回目で黒に変わっていないこまを、
　\(\,\color{blue}{2}\,\)回目ですべて黒に変えればいい。
ということです。

樹形図でも表でも良いですが、
和が\(\,6\,\)になる部分だけを書き出すと
　\(\begin{array}{|c|c|c|} \hline
\color{red}{a} & \color{blue}{b} & a+b\\ \hline
1 & 5 & 6\\ \hline
2 & 4 & 6 \\ \hline
3 & 3 & 6\\ \hline
4 & 2 & 6 \\ \hline
5 & 1 & 6\\ \hline
\end{array}\)
さいころ2つの組合わせ\(\,36\,\)通りのうち、
この\(\,5\,\)組しかありません。

答え　\(\displaystyle \underline{　\frac{5}{36}　}\)

(2)
こま\(\,\mathrm{E}\,\)の上の面が白になる確率です。

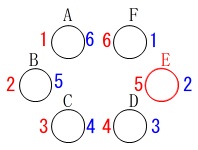
こま\(\,\mathrm{E}\,\)が白になっている場合は二通り考えられます。

　\(\,(ⅰ)\,\)\(\,1\,\)回目で黒に変わり\(\,2\,\)回目で白に戻される場合
　\(\,(ⅱ)\,\)\(\,1\,\)回目で白のままで\(\,2\,\)回目も白のままの場合

\(\,(ⅰ)\,\)の場合、
出た目が
　\(\,1\,\)回目は\(\,\color{red}{5},\color{red}{6}\,\)
　\(\,2\,\)回目は\(\,\color{blue}{2},\color{blue}{3},\color{blue}{4},\color{blue}{5},\color{blue}{6}\,\)
の\(\,\color{red}{2}\times \color{blue}{5}=10\,\)通り。

\(\,(ⅱ)\,\)の場合、
出た目が
　\(\,1\,\)回目は\(\,\color{red}{1},\color{red}{2},\color{red}{3},\color{red}{4}\,\)
　\(\,2\,\)回目は\(\,\color{blue}{1}\,\)
の\(\,\color{red}{4}\times \color{blue}{1}=4\,\)通り。

よって\(\,36\,\)通りの中で\(\,14\,\)通りあります。

答え　\(\displaystyle \frac{14}{36}=\underline{　\frac{7}{18}　}\)

さいころ2つなので（\(\,2\,\)回投げるのも同じ）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\,\color{red}{1} \,& ○ & ● & ● & ● & ● & ● \\ \hline
\color{red}{2} & ○ & ● & ● & ● & ● & ● \\ \hline
\color{red}{3} & ○ & ● & ● & ● & ● & ● \\ \hline
\color{red}{4} & ○ & ● & ● & ● & ● & ● \\ \hline
\color{red}{5} & ● & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{red}{6} & ● & ○ & ○ & ○ & ○ & ○ \\ \hline
\end{array}\)
\(\,36\,\)通りを調べるだけです。
多少時間はかかっても確実に点数が取れるなら私ならやります。

あれこれ考えているより早く終わるからですが、
進めて行くと「場合」が見えてくるものです。

第５問

\(\color{black}{\fbox{5}}\)

関数と回転体の体積の融合問題です。

条件
　点\(\,\mathrm{A,B}\,\)は関数\(\displaystyle \,y=\frac{1}{4}\,x^2\,\)上の点
　\(\,\mathrm{A,B}\,\)の\(\,x\,\)座標はそれぞれ\(\,-6\,,\,2\,\)
　点\(\,\mathrm{C}\,\)は\(\,y\,\)軸上の点
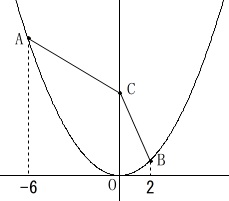\(\,\mathrm{A,B}\,\)の\(\,x\,\)座標は分かっているので、
座標そのものが分かります。
　\(\,\mathrm{A}\,(\,-6\,,\,9\,)\,\)
　\(\,\mathrm{B}\,(\,2\,,\,1\,)\,\)

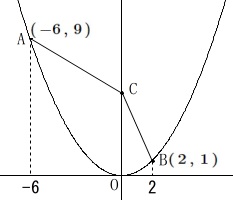
(1)
点\(\,\mathrm{A}\,\)の座標は出ています。

答え　\(\,\underline{　(\,-6\,,\,9\,)　}\,\)

(2)
線分の和\(\,\mathrm{AC+CB}\,\)が最小となるときの、
\(\,\mathrm{C}\,\)の座標を求めます。

折れ線の和が最小になるのは直線になるときです。
つまり、
直線\(\,\mathrm{AB}\,\)と\(\,y\,\)軸（\(\,x=0\,\)）との交点が求める\(\,\mathrm{C}\,\)の座標です。

\(\,2\,\)点
　\(\,\mathrm{A}\,(\,-6\,,\,9\,)\,\)
　\(\,\mathrm{B}\,(\,2\,,\,1\,)\,\)
を通る直線は
　\(\hspace{10pt}y=-x+3\)

よって\(\,\mathrm{AC＋CB}\,\)が最小になるときの\(\,\mathrm{C}\,\)の座標は
　\(\hspace{10pt}\mathrm{C}\,\underline{　(\,0\,,\,3\,)　}\)

(3)
条件が加わります。

条件
　\(\,2\,\)点\(\,\mathrm{A,B}\,\)から\(\,y\,\)軸に垂線を引き、
　\(\,y\,\)軸との交点をそれぞれ\(\,\mathrm{D,E}\,\)とする。
　点\(\,\mathrm{C}\,\)は線分\(\,\mathrm{DE}\,\)上にある。
　\(\,\mathrm{△ACD}\,,\,\mathrm{△CEB}\,\)を\(\,y\,\)軸を軸に回転させる。
　\(\,\mathrm{△ACD}\,\)の回転体の体積は\(\,\mathrm{△CEB}\,\)の回転体の体積の\(\,7\,\)倍
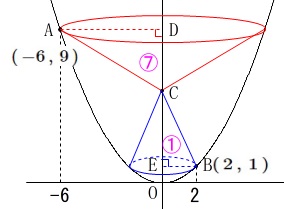このときの\(\,\mathrm{CE}\,\)の長さを求めます。

方法は1つではありませんが、
回転体が円すいであることと、
2つの円すいの底面の半径がそれぞれ分かっていることから、
直接\(\,\mathrm{CE}=\color{magenta}{h}\,\)とおいて求めることにします。
（文字は何でも良いです。）

線分\(\,\mathrm{DE}\,\)の長さは\(\,y\,\)座標の差から\(\,\color{red}{8}\,\)なので
　\(\hspace{4pt}\mathrm{CE}=\color{magenta}{h}\)
とすると
　\(\hspace{4pt}\mathrm{DC}=\color{magenta}{8-h}\)

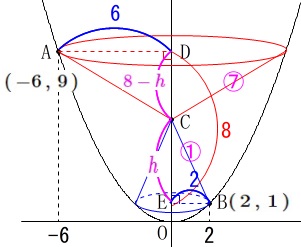
また底面の半径は\(\,\mathrm{A,B}\,\)の\(\,x\,\)座標の絶対値なので
　\(\,\mathrm{\mathrm{AD}=\color{blue}{6}}\,\)
　\(\,\mathrm{BE}=\color{blue}{2}\,\)

\(\,\mathrm{△ACD}\,\)の回転体の体積を\(\,V_1\,\)とすると
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \pi\,(6)^2\times (8-h)\\
&=&\frac{1}{3}\times 36\,\pi\,(8-h)
\end{eqnarray}\)

\(\,\mathrm{△CEB}\,\)の回転体の体積を\(\,V_2\,\)とすると
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \pi\,(2)^2\times h\\
&=&\frac{1}{3}\times 4\,\pi\,h
\end{eqnarray}\)

ここで\(\,V_1\,\)は\(\,V_2\,\)の\(\,7\,\)倍なので
　\(\begin{eqnarray}\displaystyle
\frac{V_1}{V_2}&=&7\\
\frac{36\,\pi\,(8-h)}{4\,\pi\,h}&=&7\\
\frac{9(8-h)}{h}&=&7\\
9(8-h)&=&7h\\
72-9h&=&7h\\
72&=&16h\\
\frac{9}{2}&=&h
\end{eqnarray}\)

よって
　\(\hspace{4pt}\displaystyle \mathrm{CE}=\underline{　\frac{9}{2}　}\)

もちろん比例式で
　\(\hspace{4pt}V_1:V_2=7:1\)
として求めても良いですよ。

　\(\begin{eqnarray}\displaystyle
V_1:V_2&=&7:1\\
36\,\pi\,(8-h):4\,\pi\,h&=&7:1\\
9(8-h):h&=&7:1\\
7h&=&9(8-h)\\
16h&=&72\\
h&=&\frac{9}{2}
\end{eqnarray}\)

いずれにしてもどちらも円すいなので、
\(\displaystyle \frac{1}{3}\,\)は計算せずに残して約分で無くしています。

それと\(\,\mathrm{C}\,(\,0\,,\,b\,)\,\)とおいて、
一度\(\,\mathrm{C}\,\)の座標を求めてから\(\,\mathrm{CE}\,\)を求めても良いです。
この程度の問題なら思いついた方法で突っ走っても大して変わりません。

この問題、\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,6\,\)とするとさらなる応用問題が考えられます。

第６問

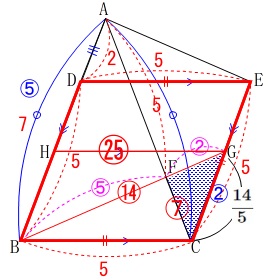
\(\color{black}{\fbox{6}}\)

平面図形における三角形の合同の証明と面積比です。

条件
　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{BC=BD}\,\)
　四角形\(\,\mathrm{BCED}\,\)はひし形
　\(\,\mathrm{AD=CF}\,\)
（\(\,\mathrm{AB\,＞\,BC}\,\)は図の通りなので深く考えなくて良いです。）
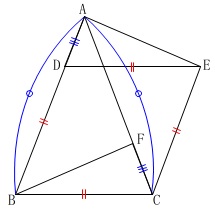長さがないのでまだ相似しか見えてこないですね。

(1)
\(\,\mathrm{△ADE}\,\)≡\(\,\mathrm{△FCB}\,\)を証明します。
（合同は相似比\(\,1:1\,\)の相似です。）
図の中で証明は終わっていますのでまとめときます。

（証明）
　\(\,\mathrm{△ADE}\,\)と\(\,\mathrm{△FCB}\,\)において
仮定から
　\(\,\mathrm{AD=FC}　･･･①\,\)
四角形\(\,\mathrm{BCED}\,\)はひし形で平行四辺形でもあるので、
　\(\,\mathrm{DE=BC}　･･･②\,\)
さらに同位角が等しく
　\(\mathrm{∠ADE=\color{red}{∠ABC}}　･･･③\)
また、\(\,\mathrm{△ABC}\,\)は二等辺三角形なので
　\(\mathrm{\color{red}{∠ABC}=∠ACB}　･･･④\)
\(\,③④\,\)より
　\(\,\mathrm{∠ADE=∠ACB}　･･･⑤\,\)
\(\,⑤\,\)はすなわち
　\(\,\mathrm{∠ADE=∠FCB}　･･･⑥\,\)
なので\(\,①②⑥\,\)より
　\(\,2\,\)組の辺とその間の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ADE}\,\)≡\(\,\mathrm{△FCB}\,\)
（終わり）

(2)
ひし形と三角形の面積比の問題です。
条件が加わります。

条件
　\(\,\mathrm{BF}\,\)の延長と\(\,\mathrm{CE}\,\)との交点を\(\,\mathrm{G}\,\)
　\(\,\mathrm{AB=7}\,\)
　\(\,\mathrm{BC=5}\,\)
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。
（求めるのが面積比なので単位がそろっていれば関係ありません。）
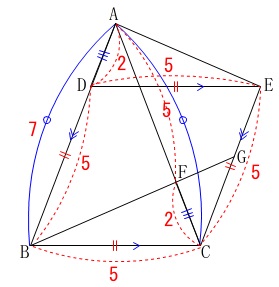比は入れていませんがわかる長さを書き込みました。

ひし形\(\,\mathrm{BCED}\,\)の面積は\(\,\mathrm{△CGF}\,\)の面積の何倍かを求めます。
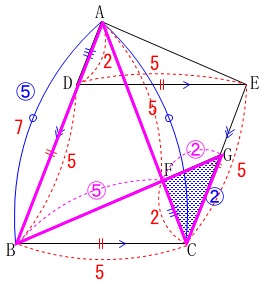方針はいくつか立ちますが、
先に相似を利用した線分比で見ていきます。

相似比のみで面積比を求める方法

ひし形\(\,\mathrm{BCED}\,\)の面積を\(\,S\,\)としておきます。

\(\,\mathrm{AB}\,\)∥\(\,\mathrm{GC}\,\)なので
　\(\,\mathrm{△ABF}\,\)∽\(\,\mathrm{△CGF}\,\)

相似比が\(\,5:2\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:GC}&=&5:2\\
7:\mathrm{GC}&=&5:2\\
5\mathrm{GC}&=&2\times 7\\
\mathrm{GC}&=&\frac{14}{5}
\end{eqnarray}\)
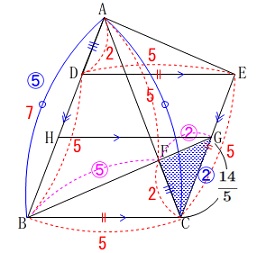\(\,\mathrm{HG}\,\)∥\(\,\mathrm{BC}\,\)となるように平行線を引くと、
ひし形の面積\(\,S\,\)と平行四辺形\(\,\mathrm{BCGH}\,\)の面積\(\,S_2\,\)との比は
　\(\begin{eqnarray}\displaystyle
S:S_2&=&5:\frac{14}{5}\\
&=&25:14\\
25\,S_2&=&14\,S\\
S_2&=&\frac{14}{25}\,S
\end{eqnarray}\)
さらに\(\,\mathrm{△BCG}\,\)はその半分で
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCG}&=&\frac{1}{2}\times \frac{14}{25}\,S\\
&=&\frac{7}{25}\,S
\end{eqnarray}\)

相似比\(\,5:2\,\)から
　\(\hspace{4pt}\mathrm{BF:GF}=5:2\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△CGF}&=&\frac{2}{5+2}\times \mathrm{△BCG}\\
&=&\frac{2}{7}\times \frac{7}{25}\,S\\
&=&\frac{2}{25}\,S
\end{eqnarray}\)

よって、
　\(\hspace{4pt}\displaystyle \underline{　\frac{25}{2}　倍}\)

相似比利用としては難しくはありませんが、
もう少し楽な方針もあります。

合同な三角形を利用する方法

(1)で証明した合同な三角形を利用します。
\(\,\mathrm{△ADE}\,\)の上に合同な三角形を加えると、
四角形\(\,\mathrm{ADEK}\,\)も平行四辺形となります。

このとき
　\(\hspace{4pt}\,\mathrm{AD:DB=\color{red}{2}:\color{red}{5}}\,\)
なので平行四辺形\(\,\mathrm{ADEK}\,\)の面積を\(\,S_3\,\)とでもすると、
（ひし形\(\,\mathrm{BCED}\,\)の面積は\(\,S\,\)のままです。）
　\(\hspace{4pt}\displaystyle S_3=\frac{2}{5}\,S\)

\(\,\mathrm{△ADE}\,\)と合同な\(\,\mathrm{△FCB}\,\)は面積が同じで、
\(\,S_3\,\)の半分なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ADE}&=&\mathrm{△FCB}\\
&=&\frac{1}{2}\times S_3\\
&=&\frac{1}{2}\times \frac{2}{5}\,S\\
&=&\frac{1}{5}\,S
\end{eqnarray}\)

ここで\(\,\mathrm{BF:FG=\color{magenta}{5}:\color{magenta}{2}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△CGF}&=&\frac{2}{5}\times \mathrm{△FCB}\\
&=&\frac{2}{5}\times \frac{1}{5}\,S\\
&=&\frac{2}{25}\,S
\end{eqnarray}\)

つまり、\(\,\mathrm{△CGF}\,\)の面積は、
ひし形\(\,\mathrm{BCED}\,\)の面積\(\,S\,\)の
　\(\hspace{4pt}\displaystyle \underline{　\frac{25}{2}　倍}\)

この問題は(1)の証明はなくても答えは出せるので、
(1)で誘導しているのではなく、
（誘導が使えれば楽にはなりますが）
答えまでの道筋を増やしてくれていると見て良いでしょう。

他にも線分の長さ、線分比が求められるので、
違う経路で求めることもできます。

1つだけ避けたい方法はひし形の面積を具体的に求めることです。
「何倍か」というのは比を聞いているのと同じことなので、
相似比から線分比を利用して進めて行くと良いですよ。

実の試験会場では別に構わないんですけどね。
「何が何でも答えを出す！」
というあきらめない泥臭い方法も嫌いではありません。

ただ、事前に準備する「対策」ということからいえば、
方法をいくつか用意できていると入試で少しは有利になるので、
『覚え太郎』『超え太郎』にひと月でも取り組んでみてください。

以上です。

⇒　高知県公立高校入試の数学の過去問題と解答解説

『覚え太郎』会員は満点が狙えます。
ただ、満点だけが合格するわけでもありません。
『最大得点法』を見直して、最低でも８割は取ってきてください。