２０２１年度埼玉県公立高校入試数学【学校選択問題】の解説

２０２１年（令和３年）度埼玉県公立高校入試数学【学校選択問題】の解説です。
この年度は一部の出題削除項目がありますが、広い基礎と応用で成り立つ問題だということは感じておきましょう。
一般問題との重複問題があるので重複部分の解説は簡単に済ませておきます。

２０２１年度埼玉県公立高校入試数学【学校選択問題】の問題

埼玉県では２０２１年度は出題に一部削除された項目があります。

⇒　2021年度埼玉県公立高校入試の学校選択問題

ここでは問題の注意書きと解答用紙を省いてあります。

２０２１年度埼玉県公立高校入試数学【学校選択問題】の解説

一般入試と同じ問題は一般入試の解説を参考にしてください。
（同じ問題にはリンク先で確認できるようにしておきます。）

学校選択問題の受験をする人は
基礎はある程度できているものとして簡単に済ませます。

第１問

\(\,\large{1}\,\)

小問が\(\,10\,\)題あります。

(1)
文字式の計算です。

　\(\hspace{10pt}\displaystyle \frac{4x-y}{2}-(2x-3y)\\
\displaystyle =\frac{(4x-y)-2(2x-3y)}{2}\\
\displaystyle =\frac{4x-y-4x+6y}{2}\\
\displaystyle =\underline{　\frac{5y}{2}　}\)

分数の計算は分母を１つにして、（通分して）
分子の計算に集中しましょう。

分子には（かっこ）がついていいることは忘れずに。

(2)
代入計算です。

これは方法が分かれたと思いますが、
与式（求値式）の変形からした人が多いかもしれません。

　\(\hspace{10pt}x^2-6x+y^2-6y\\
=(x-3)^2-9+(y-3)^2-9\\
=(x-3)^2+(y-3)^2-18\)

ここで条件式から
　\(\hspace{10pt}x-3=\color{red}{\sqrt{5}}\)
　\(\hspace{10pt}y-3=\color{blue}{-\sqrt{5}}\)
なので
　\(\hspace{10pt}(x-3)^2+(y-3)^2-18\\
=(\color{red}{\sqrt{5}})^2+(\color{blue}{-\sqrt{5}})^2-18\\
=5+5-18\\
=\underline{　-8　}\)

または、式の形から
　\(\hspace{10pt}x^2-6x+y^2-6y\\
=x^2+y^2-6x-6y\\
=(x+y)^2-2xy-6(x+y)\)
と変形して、
条件式から
　\(\begin{eqnarray}\color{red}{x+y}&=&(3+\sqrt{5})+(3-\sqrt{5})\\
&=&6\end{eqnarray}\)
および
　\(\begin{eqnarray}\color{blue}{xy}&=&(3+\sqrt{5})(3-\sqrt{5})\\
&=&4\end{eqnarray}\)
なので
　\(\hspace{10pt}(\color{red}{x+y})^2-2\color{blue}{xy}-6(\color{red}{x+y})\\
=(6)^2-2(4)-6(6)\\
=\underline{　-8　}\)
とした受験生もいるでしょう。

もう一つ、これが一番多かったと思われます。

条件式の形を見て
　\(\begin{eqnarray}
x&=&3+\sqrt{5}\\
x-3&=&\sqrt{5}\\
\end{eqnarray}\)
両辺を平方して
　\(\begin{eqnarray}
(x-3)^2&=&5\\
x^2-6x+9&=&5\\
\color{red}{x^2-6x}&=&-4
\end{eqnarray}\)
同様に
　\(\begin{eqnarray}
\color{blue}{y^2-6y}&=&-4
\end{eqnarray}\)
よって、
　\(\hspace{10pt}\color{red}{x^2-6x}+\color{blue}{y^2-6y}\\
=(-4)+(-4)\\
=\underline{　-8　}\)

たいして変わらないのでどれでも良いですが、
直接代入するような算数をするのは、
時間が余って見直しするときだけにしましょう。

いやいや、
こんなところで時間を取っている場合ではありません。
先に進みます。

(3)
２次方程式を解きます。

　\(\hspace{4pt}(2x+1)^2-7(2x+1)=0\)

展開して解の公式、は最終手段にしておきましょう。

　\(2x+1=\color{red}{t}\)
とおくと方程式は
　\(\begin{eqnarray}t^2-7t&=&0\\
t\,(t-7)&=&\\
\color{red}{t}&=&0\,,\,7
\end{eqnarray}\)
よって、
　\(\begin{eqnarray}\displaystyle
2x+1&=&0\,,\,7\\
2x&=&-1\,,\,6\\
x&=&\underline{　-\frac{1}{2}\,,\,3　}
\end{eqnarray}\)

もちろん、
　\(2x+1=0\,,\,2x+1=7\)
は別々に解けば良いですよ。

(4)(5)(6)
一般入試問題\(\,\large{1}\,\)と同じです。

　(4)は一般入試の(10)
　(5)は(13)
　(6)は(15)
と同じ問題になります。

⇒　２０２１年度埼玉県公立高校入試数学【一般問題】の解説

(7)
これも考え方は一般問題(12)と同じで良いですが、
見取り図まで示しておきます。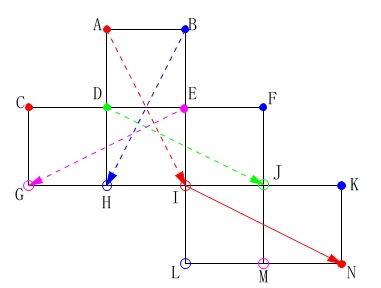二マスの対角線移動で、
立方体の対角線の移動になることと、
２回行えば元の点に戻るのは一般問題と同じです。ねじれの位置になる辺でア～エの中にあるのは１つだけです。

答え　\(\,\underline{　ウ　辺\,\mathrm{LM}　}\,\)

(8)
連立方程式の基本文章題です。

昨年度の、
　市内在住の生徒数を\(\,x\,\)
　市外在住の生徒数を\(\,y\,\)
とします。

昨年度の全生徒数は\(\,500\,\)人。
　\(\hspace{4pt}x+y=500　･･･①\)

今年度の、
　市内在住の生徒数は\(\,\displaystyle \frac{80}{100}\,x\)
　市外在住の生徒数は\(\,\displaystyle \frac{130}{100}\,y\)
全生徒数は変わらないので
　\(\hspace{4pt}\displaystyle \frac{80}{100}\,x+\frac{130}{100}\,y=500　･･･②\)

連立すると
　\( \begin{cases}
\hspace{4pt} x+y=500　･･･①\\
\hspace{4pt}\displaystyle \frac{80}{100}\,x+\frac{130}{100}\,y=500　･･･②
\end{cases}\)

\(\,①②\,\)から
　\(\hspace{4pt}x=300\,,\,y=200\)

求めるのは今年度の市内在住の生徒数なので
　\(\hspace{10pt}\displaystyle \frac{80}{100}\,x\\
\displaystyle =\frac{80}{100}\times (300)\\
=\underline{　240　}　(人)\)

『覚え太郎』会員にはクドいと言われそうですが、笑
年度別に比較がある問題では、
基準になる年の数値を文字でおきます。

求める『答え』は‘今年度’なので間違えないようにしましょう。

(9)
同じ色の玉を取り出す確率を求めます。

取り出した玉は元に戻すので注意しておきましょう。

同じ色の玉を区別して樹形図で良いですよ。
ここでは表にしておきます。
（実際には樹形図の方が早いです。）
ただし、表中の
　\(\,\color{red}{1}\,,\,\color{red}{2}\,,\,\color{red}{3}\,\)は赤玉
　\(\,4\,,\,5\,\)は白玉
を意味しています。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
１回目 & ２回目 & & １回目 & ２回目 & \\ \hline
\color{red}{1} & \color{red}{1} & ○ & 4 & \color{red}{1} & \\ \hline
\color{red}{1} & \color{red}{2} & ○ & 4 & \color{red}{2} & \\ \hline
\color{red}{1} & \color{red}{3} & ○ & 4 & \color{red}{3} & \\ \hline
\color{red}{1} & 4 & & 4 & 4 & ○\\ \hline
\color{red}{1} & 5 & & 4 & 5 & ○\\ \hline
\color{red}{2} & \color{red}{1} & ○ & 5 & \color{red}{1} & \\ \hline
\color{red}{2} & \color{red}{2} & ○ & 5 & \color{red}{2} & \\ \hline
\color{red}{2} & \color{red}{3} & ○ & 5 & \color{red}{3} & \\ \hline
\color{red}{2} & 4 & & 5 & 4 & ○\\ \hline
\color{red}{2} & 5 & & 5 & 5 & ○\\ \hline
\color{red}{3} & \color{red}{1} & ○ & & \\ \hline
\color{red}{3} & \color{red}{2} & ○ & & & \\ \hline
\color{red}{3} & \color{red}{3} & ○ & & & \\ \hline
\color{red}{3} & 4 & & & & \\ \hline
\color{red}{3} & 5 & & & & \\ \hline
\end{array}\)

答え　\(\displaystyle \underline{　\frac{13}{25}　}\)

同じ色が出るのは
　１回目赤で２回目も赤
　１回目白で２回目も白
の２つの場合があるので
　\(\hspace{10pt}\displaystyle \frac{3}{5}\times \frac{3}{5}+\frac{2}{5}\times \frac{2}{5}\\
\displaystyle =\frac{9}{25}+\frac{4}{25}\\
\displaystyle =\underline{　\frac{13}{25}　}\)

とした人もいるでしょう。
どちらでも構いません。

(10)
これも一般問題と考え方は同じです。

文字を残した計算になるだけなので説明は省略します。
一般問題を参考にしておくと良いです。アの長さは
　\(\hspace{10pt}\color{red}{14\,r}+\color{blue}{2\,\pi\,r}\)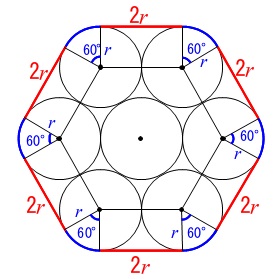イの長さは
　\(\hspace{10pt}\color{red}{12\,r}+\color{blue}{2\,\pi\,r}\)

よって、ひもの長さの差は
　\(\hspace{10pt}(14\,r+2\,\pi\,r)-(12\,r+2\,\pi\,r)\\
=\underline{　2\,r　(\mathrm{cm})}\)

弧の部分の和がそれぞれ\(\,2\,\pi\,r\,\)なので、
直線部分の差が、
アとイの長さの差になることがいえていれば良いです。

第２問

\(\,\large{2}\,\)
一般問題と似た条件ですが求めるものが違います。

(1)
２直線\(\,\ell\,,\,m\,\)から等しい距離にあり、
２点\(\,\mathrm{A\,,\,B}\,\)から等しい距離にある点\(\,\mathrm{P}\,\)を作図します。

２直線から等しい点の集まりは
　「角の二等分線」
２点から等しい点の集まりは
　「垂直二等分線」
なので
　『角の二等分線と垂直二等分線の交点』
が点\(\,\mathrm{P}\,\)です。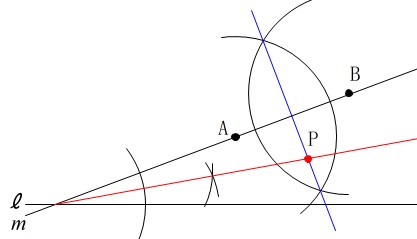

(2)
座標上にある三角形の回転体の体積を求めますが、
条件を書き出せば単なる円錐の体積です。

\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標が分かっているので、
座標で表しておきます。

条件
　関数　\(\displaystyle y=\frac{1}{2}\,x^2\)
　\(\,\displaystyle\mathrm{ A}\,\left(\,-3\,,\,\frac{9}{2}\,\right)\)
　\(\,\mathrm{B}\,(\,2\,,\,2\,)\)

２点\(\,\mathrm{A\,,\,B}\,\)を通る直線\(\,\ell\,\)の式は
　\(\hspace{4pt}\displaystyle \ell\,:\,y=-\frac{1}{2}\,x+3\)
なので\(\,x\,\)軸との交点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,\color{red}{6}\,\)です。
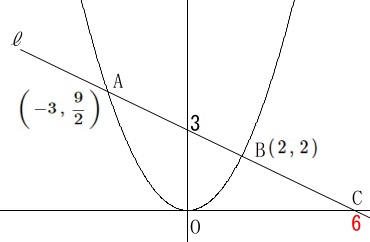　\(\,\mathrm{△AOC}\,\)を\(\,x\,\)軸を軸として回転させると
三角錐から三角錐をくり抜いた形になります。

底面の半径は
点\(\,\mathrm{A}\,\)の\(\,y\,\)座標から\(\hspace{2pt}\displaystyle \color{red}{\frac{9}{2}}\)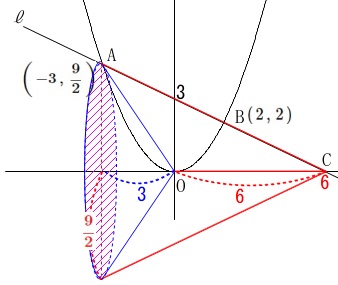
よって求める回転体の体積\(\,\mathrm{V}\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi\,\left(\frac{9}{2}\right)^2\times \color{red}{6}\\
&=&\frac{1}{3}\times \frac{81}{4}\,\pi\times 6\\
&=&\underline{　\frac{81}{2}\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

少し説明を加えておくと、
点\(\,\mathrm{C}\,\)を頂点とする円錐の体積\(\,\mathrm{V_1}\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{V_1}&=&\frac{1}{3}\times \,\pi\,\left(\frac{9}{2}\right)^2\times 9\\
&=&\frac{1}{3}\times \color{red}{\frac{81}{4}\,\pi}\times 9
\end{eqnarray}\)

点\(\,\mathrm{O}\,\)を頂点とする円錐の体積\(\,\mathrm{V_2}\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\,\pi\,\left(\frac{9}{2}\right)^2\times 3\\
&=&\frac{1}{3}\times \color{red}{\frac{81}{4}\,\pi}\times 3
\end{eqnarray}\)

これから\(\,\mathrm{V_1-V_2}\,\)を計算しても良いですが、
底面積は同じなので、
高さの差が求める回転体の高さとしても同じです。

第３問

\(\,\large{3}\,\)
規則性と文字式と割ったあまり（剰余）の問題です。

一般入試と数字の列は同じです。

(1)
これは一般問題の\(\,3\,\)(2)と同じなので
簡単にまとめておきます。

（証明）
　「\(\,n\,\)を\(\,0\,\)以上の整数とすると、」
\(\,4\,\)で割ると\(\,1\,\)余る自然数は\(\,4n+1\,\)とおける。
そこで\(\,x=4n+1\,\)を\(\,3x+5\,\)に代入すると、
　\(\begin{eqnarray}\displaystyle
3x+5&=&3(4n+1)+5\\
&=&12n+8\\
&=&4(3n+2)
\end{eqnarray}\)
ここで\(\,3n+2\,\)は自然数なので
\(\,3x+5\,\)は\(\,4\,\)の倍数である。
（終わり）

「自然数なので」は「整数なので」でも大丈夫です。

(2)
規則性を見抜くだけの簡単な【予想】です。

数字を当てはめるだけなので、
なんとなくは答えが出るでしょう。

【\(\,\mathrm{B}\,\)さんの予想】
\(\,3x+5\,\)が\(\,7\,\)の倍数になるのは、
　\(\hspace{4pt}x=3\,,\,10\,,\,\cdots\)
ですが次は、と書きだしてみると
　\(\begin{array}{|c|c|c|c|c|} \hline
x & 3 & 10 & 17 & \cdots \\ \hline
3x+5 & 14 & 35 & 56 & \cdots \\ \hline
\end{array}\)

\(\,x\,\)が\(\,7\,\)増えると\(\,3x+5\,\)は\(\,21\,\)増えるので、
\(\,7\,\)の倍数になる\(\,x\,\)から\(\,7\,\)ずつ増えても
\(\,3x+5\,\)は\(\,7\,\)の倍数になるので予想は正しいです。

つまり、
　\(\hspace{4pt}x=3\,,\,10\,,\,17\,,\,\cdots\)

　\(\hspace{4pt}3=\color{red}{7}\times 0+\color{blue}{3}\)
　\(\hspace{4pt}10=\color{red}{7}\times 1+\color{blue}{3}\)
　\(\hspace{4pt}17=\color{red}{7}\times 2+\color{blue}{3}\)
　\(\hspace{4pt}\cdots\)
　\(\hspace{4pt}x=\color{red}{7}\times m+\color{blue}{3}\)

\(\,x\,\)に\(\,7\,\)で割ると\(\,3\,\)余る数を代入すると
\(\,3x+5\,\)は\(\,7\,\)の倍数になります。

答え　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　7　}\,\)　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　3　}\,\)

【\(\,\mathrm{C}\,\)さんの予想】
\(\,(3x+5)^2\,\)を\(\,3\,\)で割ると余りは何になるかです。

これは文字式を展開すればすぐに答えは出ます。

　\(\hspace{10pt}(3x+5)^2\\
=9x^2+30x+25\\
=3(3x^2+10+8)+1\)

\(\,3x^2+10+8\,\)は自然数なので、
\(\,3\,\)で割ると余りは\(\,1\,\)となります。

答え　\(\color{black}{\fbox{　ウ　}}\)　\(\,\underline{　1　}\,\)

「\(\,3x+5\,\)を\(\,3\,\)で割ると余りは\(\,2\,\)」
という部分を利用すると
　\(\hspace{4pt}3x+5=3(x+1)+2\)
で\(\,3\,\)の倍数部分を\(\,a\,\)とすると
　\(\hspace{4pt}3x+5=a+2\)

このとき
　\(\begin{eqnarray}\displaystyle
(3x+5)^2&=&(a+2)^2\\
&=&a^2+4a+4\\
&=&(a^2+4a+3)+1
\end{eqnarray}\)

\(\,(a^2+4a+3)\,\)の部分が\(\,3\,\)の倍数なので、
全体を\(\,3\,\)で割ると\(\,1\,\)余ります。

学校選択問題なので受験生はいずれ知ることになりますが、
これを発展させて予想すると、
　\(\,x\,\)を\(\,a\,\)で割った余りが\(\,b\,\)のとき
　\(\,x^n\,\)を\(\,a\,\)で割った余りは、
　\(\,b^n\,\)を\(\,a\,\)で割った余りになる。

となります。
高校生の内容になるので進学先で学んでください。

第４問

\(\,\large{4}\,\)
一般問題と全体の条件は同じです。

条件
　\(\,\mathrm{∠ABC=∠ACD}\,\)
　\(\,\mathrm{∠BCE=∠DCE}\,\)
　\(\,\mathrm{AD=4}\,\)
　\(\,\mathrm{AC=6}\,\)
(1)
一般問題\(\,4\,\)の(2)と同じです。

一般問題の(1)の証明問題により、
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ACD}\,\)が相似であることを利用して求めています。

内角の二等分線定理を使って求めていますので
確認しておいてください。

⇒　２０２１年度埼玉県公立高校入試数学【一般問題】の解説

答え　\(\,\mathrm{BE=\underline{　3　}　(cnm)}\,\)

(2)
学校選択問題では(2)が証明問題です。

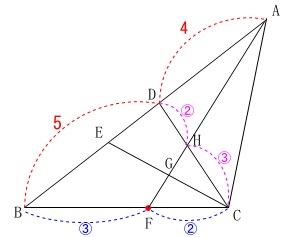
直線\(\,\mathrm{AF}\,\)が\(\,\mathrm{∠BAC}\,\)の二等分線のとき、
\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△ACF}\,\)が相似であることを証明します。
(1)の\(\,\mathrm{BE=3}\,\)から分かる長さを書き込んであります。
少し見にくいですが、ここまでは自分でやっておくことです。

証明は簡単で、
　\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△ACF}\,\)において
直線\(\,\mathrm{AF}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線であることから
　\(\,\mathrm{∠DAH=∠CAF　･･･①}\,\)
また\(\,\mathrm{△DCB}\,\)の外角\(\,\mathrm{∠ADC}\,\)について
　\(\,\mathrm{∠ADC=∠ABC+∠DCB}\,\)
ここで仮定から
　\(\,\mathrm{∠ABC=∠ACD}\,\)
なので
　\(\,\mathrm{∠ADC=∠ACD+∠DCB}\,\)
すなわち
　\(\,\mathrm{∠ADH=∠ACF　･･･②}\,\)
\(\,①②\,\)より
　２組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ADH}\,\)　∽　\(\,\mathrm{△ACF}\,\)
（終わり）

相似条件を先に見つけて、
その理由を書き出していくだけです。

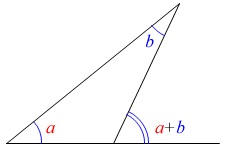三角形の１つの外角が、
　「隣の内角ではない２つの内角の和」
になる説明は必要ないでしょう。

証明は図の中で済ませておく、
というのは変わりません。

(3)
問題は一般入試と同じですが、
ここでは比だけで求めておきます。

\(\,\mathrm{△ABC=18}\,\)のとき、
\(\,\mathrm{△GFC}\,\)の面積を求めます。

角の二等分線や(2)の証明により、
線分比がほとんどわかります。
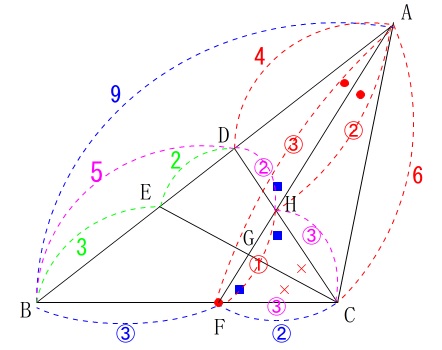『超え太郎』に目を通している人ならどうとでもなる面積です。
（もっと線分比はでていると思いますが）

簡単に説明しておくと、
(2)の\(\,\mathrm{△ADH}\,\)∽\(\,\mathrm{△ACF}\,\)から
対頂角が等しいことを加え
　\(\,\mathrm{△CHF}\,\)は二等辺三角形。
また相似比から
　\(\,\mathrm{AD:AC=AH:AF=\color{red}{②}:\color{red}{③}}\,\)
なので
　\(\,\mathrm{AH:HF=\color{red}{②}:\color{red}{①}}\,\)
であることは分かるでしょう。

後は一般入試の方でも説明しましたが、
内角の二等分線定理から、　\(\,\mathrm{AD:AC=DH:CH=\color{magenta}{②}:\color{magenta}{③}}\,\)
　\(\,\mathrm{AB:AC=BF:CF=\color{blue}{③}:\color{blue}{②}}\,\)
などが分かります。

よって、求める\(\,\mathrm{△GFC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△GFC}&=&\mathrm{△ABC}\times \frac{\color{blue}{2}}{\color{blue}{5}}\times \frac{1}{3}\times \frac{1}{2}\\
&=&18\times \frac{1}{15}\\
&=&\underline{　\frac{6}{5}　}　(\mathrm{cm^2})
\end{eqnarray}\)

これも少し説明しておくと、\(\,\mathrm{BF:CF=\color{blue}{③}:\color{blue}{②}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACF}&=&\mathrm{△ABC}\times \frac{\color{blue}{2}}{\color{blue}{3}+\color{blue}{2}}\\
&=&18\times \frac{2}{5}
\end{eqnarray}\)
また、相似比か\(\,\mathrm{らAF:HF=\color{red}{③}:\color{red}{①}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△CHF}&=&\mathrm{△ACF}\times \frac{\color{red}{1}}{\color{red}{3}}\\
&=&18\times \frac{2}{5}\times \frac{1}{3}
\end{eqnarray}\)
さらに\(\,\mathrm{△CHF}\,\)が二等辺三角形であることから、
\(\,\mathrm{△GFC}\,\)の面積は\(\,\mathrm{△AHF}\,\)の半分になります。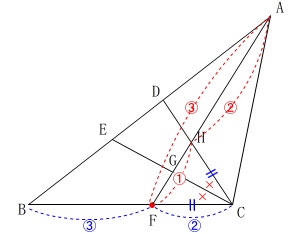
　\(\begin{eqnarray}\displaystyle
\mathrm{△GFC}&=&\mathrm{△CHF}\times \frac{1}{2}\\
&=&18\times \frac{2}{5}\times \frac{1}{3}\times \frac{1}{2}\\
&=&\frac{6}{5}
\end{eqnarray}\)

\(\,\mathrm{△CBD}\,\)側へ面積を圧縮していった人もいるでしょう。
　\(\begin{eqnarray}\displaystyle
\mathrm{△CHF}&=&△\mathrm{ABC}\times \frac{\color{red}{5}}{\color{red}{9}}\times \frac{\color{blue}{2}}{\color{blue}{5}}\times \frac{\color{magenta}{3}}{\color{magenta}{5}}\\
&=&18\times \frac{\color{red}{5}}{\color{red}{9}}\times \frac{\color{blue}{2}}{\color{blue}{5}}\times \frac{\color{magenta}{3}}{\color{magenta}{5}}\\
&=&\frac{12}{5}
\end{eqnarray}\)

会員は使える道具がたくさんあって逆に迷ったかもしれません。
　\(\hspace{4pt}\mathrm{AG:GF}=5:1\)
などもすぐに出てきたはずなので答えまでは早かったでしょう。

１つでも二等辺三角形に気がつけばどれでも良いです。
２つの二等辺三角形に気がつけばさらに良いです。
（答えを出すだけなら、気がつかなくても良いですけど。）

第５問

\(\,\large{5}\,\)

２点\(\,\mathrm{P,Q}\,\)が動く問題ですが、
良くある問題で動点問題のポイントは決まっているので機械的に済ませます。

条件
　台形\(\,\mathrm{ＡＢＣＤ}\,\)において
　\(\,\mathrm{ＡＢ=ＢＣ=5}\,\)
　\(\,\mathrm{ＣＤ=2}\,\)
　\(\,\mathrm{ＤＡ=4}\,\)
　\(\,\mathrm{∠A=∠D=90^{\circ}}\,\)
　\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)を出発して毎秒\(\,1\,\)で\(\,\mathrm{AB}\,\)上を動く。
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{A}\,\)を出発して毎秒\(\,1\,\)で\(\,\mathrm{AD,DC,CB}\,\)上を順に動く。
　\(\,\mathrm{P,Q}\,\)が出発してからの時間を\(\,x\,\)秒とする。
　\(\,\mathrm{△APQ}\,\)の面積を\(\,y\,\)とする。長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。

動点問題では、
「変化のあるところで区切る」
ことがポイントになります。
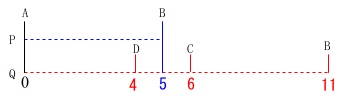分けなくても良い点があるとしても、
変化のあるところを区切れば確実に調べることができます。

　\(\,①\,0\,≦\,x\,≦\,4\,\)
　\(\,②\,4\,≦\,x\,≦\,5\,\)
　\(\,③\,5\,≦\,x\,≦\,6\,\)
　\(\,④\,6\,≦\,x\,≦\,11\,\)

等号でつながるところは頂点ですが、
「または」なので重ねても大丈夫です。
（今はあまり深く考えなくて良いということです。）

この４つの区間に分けることができれば
図を見ながら後は計算するだけ。

(1)
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{D}\,\)に到達するまでの\(\,x\,\)と\(\,y\,\)の関係です。

点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{D}\,\)に到達するためには\(\,4\,\)秒かかるので、
\(\,①\,\)の場合です。点\(\,\mathrm{Q}\,\)は辺\(\,\mathrm{AD}\,\)上にあり\(\,\mathrm{AQ}=\color{red}{x}\,\)、
点\(\,\mathrm{P}\,\)も辺\(\,\mathrm{AB}\,\)上にあり\(\,\mathrm{AP}=\color{blue}{x}\,\)です。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times x\\
&=&\underline{　\frac{1}{2}\,x^2　(\,0\,≦\,x\,≦4\,)　}
\end{eqnarray}\)

(2)
\(\,\mathrm{△APQ}\,\)と\(\,\mathrm{△AQC}\,\)の面積比が\(\,3:1\,\)になるときの\(\,x\,\)を求めます。

\(\,①\,\)のとき
（点\(\,\mathrm{Q}\,\)が\(\,\mathrm{AD}\,\)上にあり点\(\,\mathrm{P}\,\)が\(\,\mathrm{AB}\,\)上にあるとき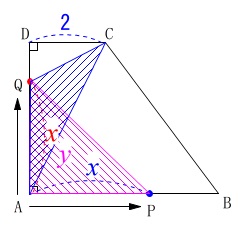）(1)より
　\(\hspace{4pt}\displaystyle \mathrm{\color{magenta}{△APQ}}=\color{magenta}{\frac{1}{2}x^2}\)
また
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△AQC}}&=&\frac{1}{2}\times x\times 2\\
&=&\color{blue}{x}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△APQ}:\color{blue}{△AQC}}&=&3:1\\
\color{magenta}{\frac{1}{2}\,x^2}:\color{blue}{x}&=&3:1\\
\frac{1}{2}\,x^2&=&3x\\
x^2-6x&=&0\\
x&=&0\,,\,6
\end{eqnarray}\)

これらは\(\,0\,≦\,x\,≦4\,\)にないので不適です。
（\(\,x=0\,\)のときは三角形になっていないので関係ありません。）

\(\,②\,\)のとき
（点\(\,\mathrm{Q}\,\)が\(\,\mathrm{DC}\,\)上にあり点\(\,\mathrm{P}\,\)が\(\,\mathrm{AB}\,\)上にあるとき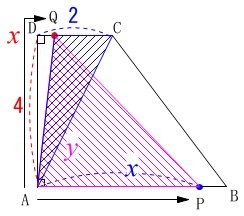）点\(\,\mathrm{Q}\,\)が\(\,\mathrm{C}\,\)まで動いたとき\(\,6\,\)なので、
\(\,\mathrm{QC}=6-x\,\)であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△APQ}}&=&\frac{1}{2}\times x\times 4\\
&=&\color{magenta}{2x}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△AQC}}&=&\frac{1}{2}\times (6-x)\times 4\\
&=&\color{blue}{2(6-x)}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△APQ}:\color{blue}{△AQC}}&=&3:1\\
\color{magenta}{2x}:\color{blue}{2(6-x)}&=&3:1\\
x&=&3(6-x)\\
4x&=&18\\
x&=&\frac{9}{2}
\end{eqnarray}\)

これは\(\,②\,4\,≦\,x\,≦\,5\,\)に適しています。

\(\,③\,\)のとき
（点\(\,\mathrm{Q}\,\)が\(\,\mathrm{DC}\,\)上にあり点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)にあるとき）点\(\,\mathrm{P}\,\)は\(\,\mathrm{B}\,\)で動かなくなっているので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△APQ}}&=&\frac{1}{2}\times 5\times 4\\
&=&\color{magenta}{10}
\end{eqnarray}\)
また\(\,\mathrm{△AQC}\,\)の面積は\(\,②\,\)のときと同じなので
　\(\hspace{4pt}\mathrm{\color{blue}{△AQC}}=\color{blue}{2(6-x)}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△APQ}:\color{blue}{△AQC}}&=&3:1\\
\color{magenta}{10}:\color{blue}{2(6-x)}&=&3:1\\
10&=&6(6-x)\\
6x&=&26\\
x&=&\frac{13}{3}
\end{eqnarray}\)

これは\(\,③\,5\,≦\,x\,≦\,6\,\)にないので不適です。

\(\,④\,\)のとき
（点\(\,\mathrm{Q}\,\)が\(\,\mathrm{CB}\,\)上にあり点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)にあるとき）点\(\,\mathrm{Q}\,\)が\(\,\mathrm{B}\,\)まで移動したとき\(\,11\,\)なので
　\(\hspace{4pt}\mathrm{\color{magenta}{PQ}}=\color{magenta}{11-x}\)
また\(\,\mathrm{CB=5}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{CQ+PQ}&=&\mathrm{CB}\\
\mathrm{\color{blue}{CQ}}&=&\mathrm{CB-PQ}\\
&=&5-(11-x)\\
&=&\color{blue}{x-6}
\end{eqnarray}\)

ここで\(\,\mathrm{△APQ}\,\)と\(\,\mathrm{△AQC}\,\)は高さを共通にしているので、
底辺の比\(\,\mathrm{PQ:CQ}\,\)が面積比になります。
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{PQ}}:\mathrm{\color{blue}{CQ}}&=&3:1\\
(\color{magenta}{11-x}):(\color{blue}{x-6})&=&3:1\\
3(x-6)&=&11-x\\
4x&=&29\\
&=&\frac{29}{4}
\end{eqnarray}\)

これは\(\,④\,6\,≦\,x\,≦\,11\,\)に適しています。

答え　\(\displaystyle x=\underline{　\frac{9}{2}\,,\,\frac{29}{4}　}\)

(3)
\(\,\mathrm{△APQ}\,\)の面積が台形\(\,\mathrm{ABCD}\,\)の半分になるときの、
\(\,x\,\)の値を求めます。

(2)で分けた区分で面積を考えれば良いですが、
途中の説明も書くように指示があるので
簡単にですがまとめておきます。

台形\(\,\mathrm{ABCD}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{2+5}{2}\times 4\\
&=&14
\end{eqnarray}\)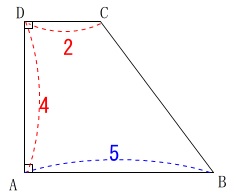つまり\(\,\mathrm{△APQ}\,\)の面積が\(\,7\,\)にあるときを求めれば良い。

ⅰ）点\(\,\mathrm{Q}\,\)が\(\,\mathrm{AD}\,\)上にあるとき
　\(\hspace{4pt}0\,≦\,x\,≦\,4\)
であり、
　\(\hspace{4pt}\displaystyle \mathrm{△APQ}=\frac{1}{2}x^2\)
なので
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\,x^2&=&7\\
x^2&=&14\\
x&=&\sqrt{14}　(\,x\,＞\,0)
\end{eqnarray}\)
これは適する。

ⅱ）点\(\,\mathrm{Q}\,\)が\(\,\mathrm{DC}\,\)上にあるとき
　\(\hspace{4pt}4\,≦\,x\,≦\,5\)
では\(\,\mathrm{△APQ}\,\)の面積は
　\(\hspace{4pt}\mathrm{△APQ}=2x\)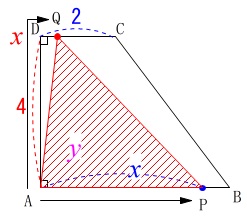であり\(\,\mathrm{△APQ}\,\)の面積が\(\,7\,\)になることはない。
また、
　\(\hspace{4pt}5\,≦\,x\,≦\,6\)
では\(\,\mathrm{△APQ}\,\)の面積は\(\,10\,\)で一定である。
よって点\(\,\mathrm{Q}\,\)が\(\,\mathrm{DC}\,\)上にあるときは条件を満たす\(\,x\,\)はない。

ⅲ）点\(\,\mathrm{Q}\,\)が\(\,\mathrm{CB}\,\)上にあるとき
　\(\hspace{4pt}6\,≦\,x\,≦\,11\)
では\(\,\mathrm{△APQ}\,\)の面積は高さが
　\(\hspace{4pt}\displaystyle \frac{4}{5}(11-x)\)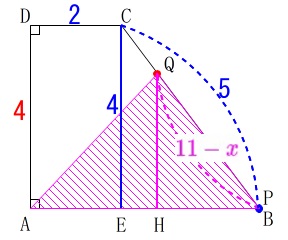
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times 5\times \frac{4}{5}(11-x)\\
&=&2(11-x)
\end{eqnarray}\)
このとき
　\(\begin{eqnarray}\displaystyle
2(11-x)&=&7\\
x&=&\frac{15}{2}
\end{eqnarray}\)
これは適する。

答え　\(\displaystyle x=\underline{　\sqrt{14}\,,\,\frac{15}{2}　}\)

ⅲ）で\(\,\mathrm{△APQ}\,\)の高さ（図の\(\,\mathrm{QH}\,\)）の求め方を書いていませんが、
　\(\,\mathrm{△CEB}\,\)　∽　\(\,\mathrm{△QHB}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{CE:QH}&=&\mathrm{CB:QB}\\
4:\mathrm{QH}&=&5:(11-x)\\
5\mathrm{QH}&=&4(11-x)\\
\mathrm{QH}&=&\frac{4}{5}(11-x)
\end{eqnarray}\)