２０２１年（令和３年）度神奈川県公立高校入試の数学問題と解説

２０２１年(令和３年)に神奈川県で行われた公立高校入試の数学の問題と解説です。
前年度から続いておりますので大問が６問に定着するようです。
神奈川県の問題はマークシート部分がありますが、
しっかり道筋立てて解かないと答えだけが簡単に出る問題ではありません。

※（昨年度の解説で書いておきました。）
神奈川県公立入試では2021年度（令和3年）の数学では「資料（データ）の活用」『標本調査』は出題されません。
ということは、ほとんど例年と変わらないということです。

２０２１年度は確かに出題されない項目がありましたが、
普通に例年通りの入試問題です。

２０２１年（令和３年）度神奈川県立高校入試の数学問題

問題は神奈川県で公開してくれています。

⇒　２０２１年(令和３年)神奈川県立高校入試の数学問題

問題は問\(\,\mathrm{1}\,\)から問\(\,\mathrm{6}\,\)まであります。
ここでは注意書きは省いてありますので
神奈川県の受験生は受験年度に確認しておきましょう。

２０２１年（令和３年）度神奈川県立高校入試の数学の解説

神奈川県の問題は記号を選ぶ問題が多いですが、
単純な計算問題から手を動かさないと答えが見えない問題まで
２０２１年度も様々な範囲と難易度での出題となっています。

このページで解説を終えておきたいですが、
問題数が多く、長くなるのでサイト内でリンクさせる部分も出てくると思います。
過去問解説などを参考にして頂くことをご了承ください。

過去問解説ですべての問題は説明済みだということはわかりますので、
ここでは（できるだけ）少なめの説明にしておきます。

問１基本計算小問集合

計算問題です。

記号を選びますが計算過程を大切にしておきましょう。

\(\,(ア)\,\)
　\(\hspace{10pt}-9-(-5)\\
=-9+5\\
=\underline{　-4　}\)

答え　\(\,2\,\)

負の数を引くのは正の数を足すのと同じです。

\(\,(イ)\,\)
　\(\hspace{10pt}\displaystyle -\frac{5}{6}-\frac{3}{4}\\
\displaystyle =\frac{-10-9}{12}\\
\displaystyle =\underline{　-\frac{19}{12}　}\)

答え　\(\,1\,\)

分数計算は人によって違うと思います。
分母を１つにして、
分子の計算に集中するとやりやすいですよ。
（『覚え太郎』会員にはいうまでもありませんが。）

\(\,(ウ)\,\)
　\(\hspace{10pt}8ab^2\times 3a\div 6a^2b\\
\displaystyle =\frac{8ab^2\times 3a}{6a^2b}\\
=\underline{　4\,b　}\)

割り算は逆数の掛け算なので
　\(\hspace{10pt}8ab^2\times 3a\div 6a^2b\\
\displaystyle =8ab^2\times 3a\times \frac{1}{6a^2b}\\
=4\,b\)
を分数線１つで計算しただけです。

\(\,(エ)\,\)
分数計算ですので\(\,(イ)\,\)と同じです。

　\(\hspace{10pt}\displaystyle \frac{3x+2y}{5}-\frac{x-3y}{3}\\
\displaystyle =\frac{3(3x+2y)-5(x-3y)}{15}\\
\displaystyle =\frac{9x+6y-5x+15y}{15}\\
\displaystyle =\underline{　\frac{4x+21y}{15}　}\)

答え　\(\,3\,\)

分子には（かっこ）がついていることは忘れないようにしましょう。

\(\,(オ)\,\)
無理数の計算です。

　\(\hspace{10pt}\color{red}{(2+\sqrt{7})(2-\sqrt{7})}+6(\sqrt{7}+2)\\
=\color{red}{(4-7)}+6\sqrt{7}+12\\
=\underline{　9+6\sqrt{7}　}\)

答え　\(\,4\,\)

展開のところで
　\(\hspace{4pt}\color{red}{(a+b)(a-b)}=\color{red}{a^2-b^2}\)
の公式を利用していますが、
地道に展開しても良いですよ。

問２方程式不等式を含む小問集合

\(\,(ア)\,\)
因数分解します。

　\(\hspace{10pt}(x+6)^2-5(x+6)-24\)

\(\,x+6=t\,\)とすると
　\(\hspace{10pt}t^2-5t-24\\
=(t-8)(t+3)\)

\(\,t=x+6\,\)を戻すと
　\(\hspace{10pt}(t-8)(t+3)\\
=(x+6-8)(x+6+3)\\
=\underline{　(x-2)(x+9)　}\)

答え　\(\,4\,\)

文字を置き換えなくて
　\(\hspace{10pt}(x+6)^2-5(x+6)-24\\
=\{(x+6)-8\}\{(x+6)+3\}\\
=(x-2)(x+9)\)
としても良いですがなれるまでは置き換える方が確実です。

もちろん展開してから因数分解しても良いです。
　\(\hspace{10pt}(x+6)^2-5(x+6)-24\\
=x^2+12x+36-5x-30-24\\
=x^2+7x-18\\
=(x-2)(x+9)\)

ただ、あからさまにまとまりがあるので「置き換え」ですね。

\(\,(イ)\,\)
２次方程式を解きます。

　\(\hspace{4pt}x^2-3x+1=0\)

因数分解できないので解の公式を利用します。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1\cdot 1}}{2}\\
&=&\frac{3\pm \sqrt{9-4}}{2}\\
&=&\underline{　\frac{3\pm \sqrt{5}}{2}　}
\end{eqnarray}\)

答え　\(\,2\,\)

\(\,(ウ)\,\)
変化の割合から比例定数を求めます。

関数\(\,y=ax^2\,\)において
　\(\,x=1\,\)のとき\(\,y=a\,\)
　\(\,x=4\,\)のとき\(\,y=16a\,\)
なので
　\(\,x\,\)の増加量は\(\,\color{red}{3}\,\)
　\(\,y\,\)の増加量は\(\,\color{blue}{15a}\,\)

　\((変化の割合)=\displaystyle \frac{　(\color{blue}{\,y\,の増加量\,})　}{　(\color{red}{\,x\,の増加量\,})　}\)
なので変化の割合が\(\,\color{magenta}{-3}\,\)であることから
　\(\begin{eqnarray}\displaystyle
\frac{\color{blue}{15a}}{\color{red}{3}}&=&\color{magenta}{-3}\\
5a&=&-3\\
a&=&\underline{　-\frac{3}{5}　}
\end{eqnarray}\)

答え　\(\,2\,\)

\(\,(エ)\,\)
重さの関係を不等式にします。

「荷物全体の重さが\(\,\mathrm{200\,kg}\,\)以上」
というのは荷物の重さの方が
\(\,200\,\)より大きいかまたは等しいということです。

　\(\hspace{4pt}\underline{　15x+9y≧200　}\)

「以上」「以下」には等号がつきます。
「より」には等号はつきません。

\(\,(オ)\,\)
ルートの付いた数が自然数になるための\(\,n\,\)の値を求めます。

　\(\hspace{4pt}\displaystyle \sqrt{\frac{540}{n}}\)

自然数になるにはルートの中が平方数にならなければなりません。
分子を素因数分解すると
　\(\hspace{10pt}540\\
=2^2\times 3^3\times 5\\
=\color{blue}{2^2}\times \color{blue}{3^2}\times \color{red}{3}\times \color{red}{5}\)

\(\,○^2\,\)となっていないところを消せば良いので
最小の\(\,n\,\)は\(\,3\times 5\,\)です。

　\(\hspace{10pt}n=\underline{　15　}\)

答え　\(\,3\,\)

⇒　ルートのついた無理数を整数や自然数に変える方法と問題の解き方

ルートの中を平方数にする自然数\(\,n\,\)は１つではありませんが、
「最も小さい自然数\(\,n\,\)」なので１つだけです。

\(\,(カ)\,\)
円に内接する五角形の対角線における角度を求めます。

条件
　\(\,4\,\)点\(\,\mathrm{A,B,C,D}\,\)は円周上の点
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
（後は問題の図の通りに記号が与えられています。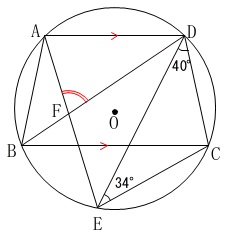）\(\,\mathrm{∠AFD}\,\)の大きさを求めます。

内接四角形の内角の性質を利用することもできますが、
円周角だけで簡単に済ませておきます。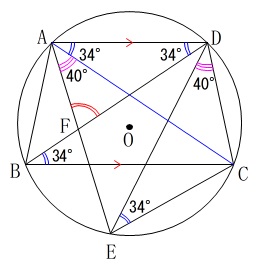対角線\(\,\mathrm{AC}\,\)を加えておきます。

弧\(\,\mathrm{DC}\,\)に対する円周角は等しいので、
　\(\hspace{4pt}\mathrm{∠DEC=∠DBC}=34^{\circ}\)
また平行線の錯角は等しいので
　\(\hspace{4pt}\mathrm{∠ADB=∠DBC}=34^{\circ}\)
弧\(\,\mathrm{EC}\,\)の円周角は等しいので
　\(\hspace{4pt}\mathrm{∠EDC=∠EAC}=40^{\circ}\)
\(\,\mathrm{△AFD}\,\)の内角の和が\(\,180^{\circ}\,\)であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AFD}&=&180^{\circ}-(\mathrm{∠FAD+∠FDA})\\
&=&180^{\circ}-108^{\circ}\\
&=&\underline{　72^{\circ}　}
\end{eqnarray}\)

条件はすべて使って答えが出るように問題は作られています。
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)を忘れないようにしましょう。

補助線に\(\,\mathrm{BE}\,\)を使っても当然ですが同じ結果になります。
補助線なしで内接四角形\(\,\mathrm{AECD}\,\)を利用することもできます。
（『覚え太郎』会員は「円と円周角」\(\,\mathrm{No.13}\,\)参照）

条件を使い切ればどれでも良いですよ。
角度は求まるように問題は作られていますから。

問３標準レベルの小問集合

\(\,(ア)\,\)
正三角形に関する平面図形の問題です。

合同の証明は記号を選ぶだけなのですぐに答えが出ますが、
長さの問題に利用できるかがポイントです。

条件
　\(\,\mathrm{△ABC}\,\)は正三角形
　\(\,\mathrm{AD=BE=CF}\,\)
（記号は問題の図\(\,1\,\)にある通りです。）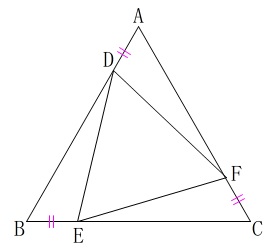
\(\,(ⅰ)\,\)
　\(\,\mathrm{△ADF}\,\)と\(\,\mathrm{△CFE}\,\)が合同であることを証明します。

図の中で証明を済ませておきましょう。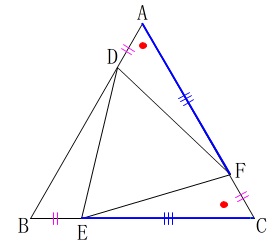合同条件は
「２組の辺と間の角がそれぞれ等しい。」
となります。

証明ではありませんが合同条件になる部分をそろえておきます。

仮定から
　\(\hspace{4pt}\mathrm{AD=CF}\)
正三角形の内角は等しいから
　\(\hspace{4pt}\mathrm{∠DAC=∠FCE}\)
また正三角形の辺はそれぞれ等しいので
　\(\hspace{4pt}\mathrm{\color{red}{AC}=\color{red}{BC}}\)
仮定から
　\(\,\mathrm{AD=\color{blue}{BE}=\color{blue}{CF}}\,\)
ここで（長さが等しい辺を引くことになるので）
　\(\hspace{4pt}\mathrm{AF=\color{red}{AC}-\color{blue}{CF}}\)
　\(\hspace{4pt}\mathrm{CE=\color{red}{BC}-\color{blue}{BE}}\)
なので
　\(\hspace{4pt}\mathrm{AF=CE}\)

答え　\(\,(\mathrm{a})　4\,\)　\(\,(\mathrm{b})　1\,\)　\(\,(\mathrm{c})　2\,\)

ここは証明の手順を知っていれば問題ないでしょう。

\(\,(ⅱ)\,\)
面積比が与えられたときの辺の長さを求めます。

条件が加わります。
　\(\,\mathrm{AB=18}\,\)
　\(\,\mathrm{AD}\,＜\,\mathrm{BD}\)
　\(\,\mathrm{△ABC:△DEF=12:7}\,\)
長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。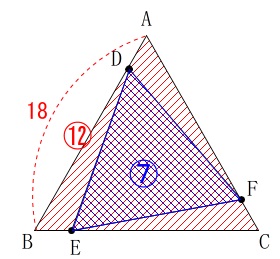求めるのは\(\,\mathrm{AD}\,\)の長さです。

面積比に関する公式を使えばすぐに答えは出るのですが、
（『覚え太郎』会員は「相似な図形」\(\,\mathrm{No.59\,,\,60}\,\)参照）
ここでは一般向けに具体的な数値を使って求めておきます。
（最後に少し会員向け解説をしておきます。）

\(\,\mathrm{△ABC}\,\)が１辺\(\,18\,\)の正三角形なので、
高さは
　\(\,\mathrm{AH=\color{red}{9\sqrt{3}}}\,\)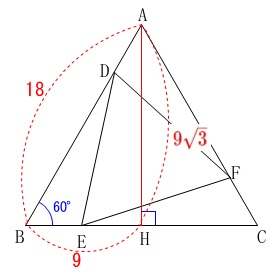正三角形\(\,\mathrm{ABC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times 18\times 9\sqrt{3}\\
&=&81\sqrt{3}
\end{eqnarray}\)

\(\,(ⅰ)\,\)で証明したことから
合同だから面積も等しいので
　\(\hspace{4pt}\mathrm{△ADF=△CFE=△BED}\)

この３つの三角形の面積の和\(\,S_1\,\)は、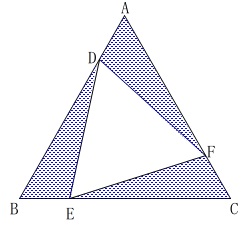
\(\,\mathrm{△ABC}\,\)から\(\,\mathrm{△DEF}\,\)を除いた面積になるので
　\(\,\mathrm{△ABC:△DEF=12:7}\,\)
であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}:S_1&=&12:5\\
S_1&=&\frac{5}{12}\times \mathrm{△ABC}\\
&=&\frac{5}{12}\times 81\sqrt{3}\\
\end{eqnarray}\)

\(\,\mathrm{△ADF}\,\)の面積は\(\,S_1\,\)を３等分した面積なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ADF}&=&\frac{1}{3}\times \frac{5}{12}\times 81\sqrt{3}\\
&=&\color{blue}{\frac{45}{4}\sqrt{3}}
\end{eqnarray}\)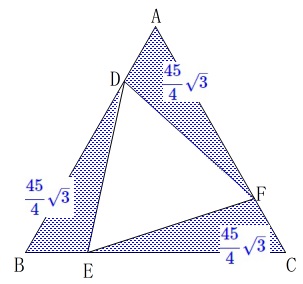
さて、準備が整いましたので\(\,\mathrm{AD}\,\)を求めます。

求めたい\(\,\mathrm{AD=CF}\,\)を\(\,\color{red}{x}\,\)とすると
　\(\,\mathrm{AF=DB}=\color{red}{18-x}\,\)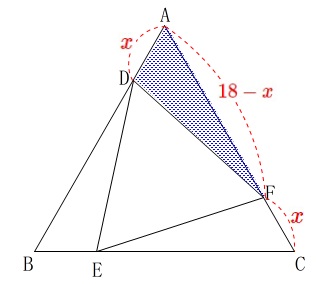\(\,\mathrm{△ADF}\,\)の底辺を\(\,\mathrm{AD}\,\)とすると
高さは\(\,\mathrm{F}\,\)から\(\,\mathrm{AB}\,\)に垂線を下ろした線分\(\,\mathrm{FK}\,\)の長さになります。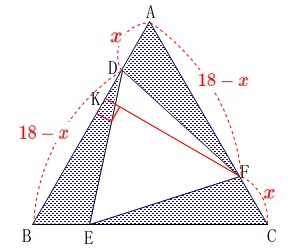\(\,\mathrm{FK}\,\)は下図の\(\,\mathrm{DI}\,\)と等しいので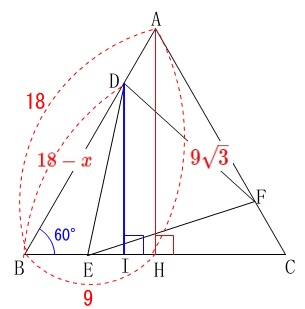
　\(\,\mathrm{△ABH}\,\)　∽　\(\,\mathrm{△DBI}\,\)
を利用します。
（こちらの都合なので\(\,\mathrm{△AFK}\,\)で求めて良いですよ。笑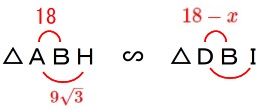）このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:DB}&=&\mathrm{AH:DI}\\
18:(18-x)&=&9\sqrt{3}:\mathrm{DI}\\
18\,\mathrm{DI}&=&(18-x)\times 9\sqrt{3}\\
\mathrm{DI}&=&\frac{(18-x)\sqrt{3}}{2}
\end{eqnarray}\)

底辺を\(\,\mathrm{AD}\,\)と見ると\(\,\mathrm{△ADF}\,\)の高さ\(\,\mathrm{FK}\,\)も同じです。

\(\,\mathrm{△ADF}\,\)の面積は
　\(\hspace{4pt}\displaystyle \mathrm{\color{blue}{△ADF}}=\frac{1}{2}\times \mathrm{AD}\times \mathrm{FK}\)
なので
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times x\times \frac{(18-x)\sqrt{3}}{2}&=&\color{blue}{\frac{45}{4}\sqrt{3}}\\
x^2-18x+45&=&0\\
(x-3)(x-15)&=&0\\
x&=&3\,,\,15
\end{eqnarray}\)

ここで\(\,\mathrm{AD\,＜\,BD}\,\)なので
　\(\hspace{4pt}x=\mathrm{AD}=\underline{　3　(\mathrm{cm})}\)

ちなみに、
『覚え太郎』「相似な図形」\(\,\mathrm{No.59\,,\,60}\,\)を使った場合\(\,\mathrm{(ⅱ)}\,\)は
　\(\begin{eqnarray}\displaystyle
3\times x(18-x)&=&18^2\times \frac{5}{12}\\
x^2-18x+45&=&0\\
(x-3)(x-15)&=&0
\end{eqnarray}\)

と高さは求める必要はありません。
（説明がいらない問題なので短時間で終わったはず。）

\(\,(イ)\,\)
資料の活用の問題です。

⇒　中学１年資料の整理(活用)の用語と特長および対策

データに関する基本はここにあります。

ここでは折れ線の相対度数を読み取れば答えは出ますが、
累積度数分布表を簡単に作成しておきます。

\(\,\mathrm{A}\,\)中学校（\(\,100\,\)人）
　\(\begin{array}{|c|c|c|c|} \hline
階級 & 相対度数 & 度数 & 累積度数\\ \hline
0～5 & 0.01 & 1 & \\ \hline
5～10 & 0.02 & 2 & 3\\ \hline
10～15 & 0.09 & 9 & 12\\ \hline
15～20 & 0.21 & 21 & 33\\ \hline
20～25 & 0.24 & 24 & 57\\ \hline
25～30 & 0.26 & 26 & 83\\ \hline
30～35 & 0.15 & 15 & 98\\ \hline
35～40 & 0.02 & 2 & 100\\ \hline
\end{array}\)
\(\,\mathrm{B}\,\)中学校（\(\,150\,\)人）
　\(\begin{array}{|c|c|c|c|} \hline
階級 & 相対度数 & 度数 & 累積度数\\ \hline
0～5 & 0.00 & 0 & \\ \hline
5～10 & 0.04 & 6 & 6 \\ \hline
10～15 & 0.12 & 18 & 24 \\ \hline
15～20 & 0.22 & 33 & 57 \\ \hline
20～25 & 0.24 & 36 & 93 \\ \hline
25～30 & 0.18 & 27 & 120 \\ \hline
30～35 & 0.16 & 24 & 144 \\ \hline
35～40 & 0.04 & 6 & 150 \\ \hline
\end{array}\)

\(\,あ\,\)
\(\,\mathrm{A}\,\)中学校の中央値は
累積度数が\(\,50,51\,\)になる階級値なので\(\,22.5\,\)

\(\,\mathrm{B}\,\)中学校の中央値は
累積度数が\(\,75,76\,\)になる階級値なので\(\,22.5\,\)

中央値は同じです。○

\(\,い\,\)
\(\,20\,\)未満の生徒の割合は累積相対度数を計算して
　\(\,\mathrm{A}\,\)中学校　\(\,0.34\,\)
　\(\,\mathrm{B}\,\)中学校　\(\,0.38\,\)

\(\,\mathrm{A}\,\)中学校の方が小さいです。×

\(\,う\,\)
\(\,20～25\,\)の階級の度数は
　\(\,\mathrm{A}\,\)中学校　\(\,57\,\)
　\(\,\mathrm{B}\,\)中学校　\(\,93\,\)

\(\,\mathrm{B}\,\)中学校の方が多いです。○

相対度数は同じですが度数合計が違うので度数も変わってきます。

\(\,え\,\)
\(\,30\,\)以上の度数は
　\(\,\mathrm{A}\,\)中学校　\(\,17\,\)
　\(\,\mathrm{B}\,\)中学校　\(\,30\,\)
\(\,25～30\,\)の階級の度数は
　\(\,\mathrm{A}\,\)中学校　\(\,26\,\)
　\(\,\mathrm{B}\,\)中学校　\(\,27\,\)

\(\,\mathrm{B}\,\)中学校は逆です。×

答え　\(\,2\,\)

\(\,(う)\,\)
水面の高さを表す１次関数の問題です。

水そうの底面が２つに分かれていますが、
毎秒入る水の量は一定ですので
別々に見ていけば難しくありません。

水そうの底面や高さの長さは問題の図３の通りなので
図に示しておきます。
（単位は\(\,\mathrm{cm}\,\)ですが省略します。）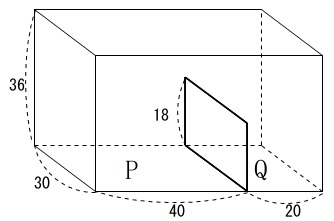
(ⅰ)
入れ始めてから水面の高さが上がり続ける、
つまり板の高さになるまでの時間を求めます。

面\(\,\mathrm{P}\,\)の底面積は
　\(\hspace{4pt}30\times 40=1200\)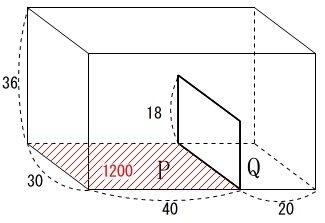
板の高さは\(\,18\,\)なので板をこえるまでの体積は
　\(\hspace{4pt}1200\times 18\)

水は一定量\(\,200\,\)で入れ続けるので
　\(\begin{eqnarray}
a&=&\frac{1200\times 18}{200}\\
&=&\underline{　108　}
\end{eqnarray}\)

実際の計算では\(\,30\times 40\,\)はそのまま進めて
最後に約分する方が早いです。

または、
１秒間に\(\,200\,\)入るので\(\,\mathrm{1\,(cm)}\,\)上昇するのに
　\(\hspace{4pt}1200\div 200=6　(秒)\)

だから\(\,18\,(\mathrm{cm})\,\)上昇するには
　\(\hspace{10pt}6\times 18\\
=108\)
でも良いですよ。

\(\,(ⅱ)\,\)
水面の高さ\(\,y\,\)と入れ始めてからの時間\(\,x\,\)
の関係を表すグラフを選びます。

答えを見つけるだけなら、
\(\,(ⅰ)\,\)で一定で増えるのは\(\,x=108\,\)まで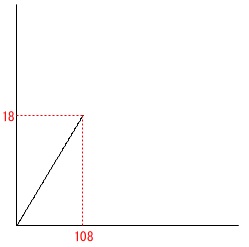ということはわかっているので
\(\,3\,,\,4\,\)のどちらかということはすぐに分かります。

高さ\(\,y\,\)が一定になるのは
底面\(\,\mathrm{Q}\,\)の部分を高さ\(\,18\,\)にするまでなので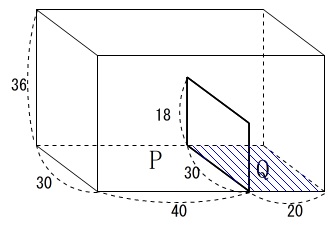
　\(\hspace{10pt}30\times 20\times 18\div 200\\
=54　(秒)\)
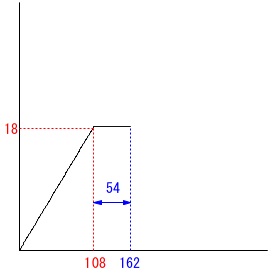\(\,54\,\)秒間高さが変化していないのでは１つです。

答え　\(\,3\,\)

板の高さを超えた後は\(\,\mathrm{1\,cm}\,\)上昇するのに
　\(\hspace{10pt}30\times 60\div 200=9　(秒)\)
だから
　\(\hspace{10pt}18\times 9=162　(秒)\)
で水そうは満水になります。
これは面\(\,\mathrm{P,Q}\,\)ともに仕切りの板の高さを超えるまでの時間と同じです。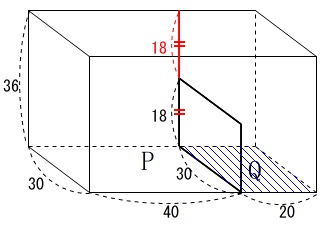
（仕切りの板の高さが水そうの高さの半分だから。）

入れ始めてからは
　\(\hspace{10pt}162+162=324　(秒)\)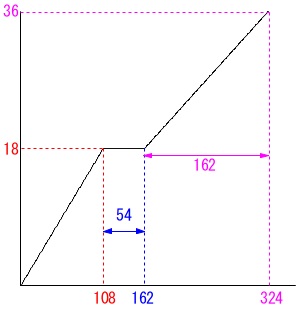それぞれの区間で関数は求まります。
ここでは必要ありませんが、
自分で求めておくと良いです。

直線は２点を結べば決まります。

\(\,(エ)\,\)
連立方程式の問題です。

穴埋め問題なので説明はいらないと思いますが、
比較がある関係では、
　「基準になるものを文字でおく」
というのが基本になります。

今週の利用者は先週と比較されているので、
先週の利用者を文字でおきます。

先週の
　大人の利用者数を\(\,x\,\)
　子どもの利用者数を\(\,y\,\)
とすると先週の利用者数は合わせて\(\,580\,\)人なので
　\(\hspace{10pt}x+y=580　･･･①\)

今週の
大人の利用者数は１割増加しているので
　大人の利用者の増加数は\(\,\displaystyle \frac{1}{10}x\)
子どもの利用者数は３割増加しているので
　子どもの利用者数の増加は\(\,\displaystyle \frac{3}{10}y\)
利用者数の増加は合わせて\(\,92\,\)人だから
　\(\hspace{4pt}\displaystyle \frac{1}{10}x+\frac{3}{10}y=92　･･･②\)

答え　\(\,(ⅰ)\,\)　\(\displaystyle \underline{　\frac{1}{10}\,x+\frac{3}{10}\,y　}\)

\(\,②\,\)は
　\(\hspace{4pt}0.1x+0.3y=92\)
としても構いません。

\(\,①②\,\)を連立して\(\,x\,,\,y\,\)を求めると
　\(\hspace{4pt}x=\underline{　410　}\,,\,y=170\)

答え　\(\,(ⅱ)\,\)　\(\,410\,\)

今週の大人の利用者数は１割増えているので
　\(\hspace{10pt}\displaystyle 410\times \frac{110}{100}\\
=\underline{　451　}\)

答え　\(\,(ⅲ)\,\)　\(\,451\,\)

増えた大人の利用者数が１割なので
　\(\hspace{4pt}\displaystyle 410\times \frac{1}{10}=41\)
だから今週の大人の利用者数は
　\(\hspace{10pt}410+41=451\)
と求めても良いです。

問題が『増えた利用者』で方程式を立てているので注意しましょう。

やっと半分終わりました。
こんなにダラダラ説明する問題ではないので先に進みましょう。

問４関数総合問題

直線が６本と放物線が１つあります。

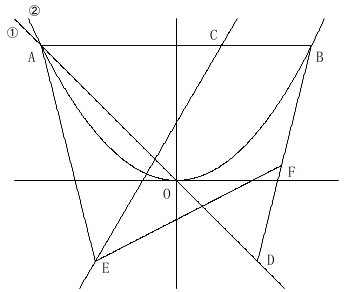
グラフが与えられているので条件を書き出しておきます。

条件
　\(\,①\,\)は\(\,y=-x\,\)
　\(\,②\,\)は\(\,y=ax^2\,\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-5\,\)
　\(\,\mathrm{AB}\,\)は\(\,x\,\)軸に平行
　\(\,\mathrm{AC:CB=2:1}\,\)
　\(\,\mathrm{AO:OD=5:3}\,\)
　\(\,\mathrm{E}\,\)は\(\,\mathrm{D}\,\)と\(\,y\,\)軸について対称

多いですが条件を整理すれば
それほどややこしくもありません。

ただし、
神奈川県では例年のことですが傾きや切片を求める段階で
分数計算が混じります。

条件から分かることを書き出して行きます。

\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,-5\,\)で
直線\(\,①\,\)上の点なので
　\(\,\mathrm{A\,(\,-5\,,\,5\,)}\,\)

\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)の\(\,y\,\)軸対称な点になるので
　\(\,\mathrm{B\,(\,5\,,\,5\,)}\,\)

点\(\,\mathrm{C}\,\)は\(\,\mathrm{AC:CB=2:1}\,\)になる点なので
\(\,\mathrm{AB=10}\,\)だから
　\(\,\displaystyle \mathrm{AC=10\times \frac{2}{3}=\color{blue}{\frac{20}{3}}}\,\)
　\(\,\displaystyle \mathrm{CB=10\times \frac{1}{3}=\color{blue}{\frac{10}{3}}}\,\)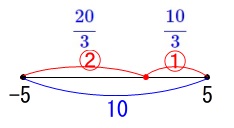
このとき\(\,\mathrm{C}\,\)の\(\,x\,\)座標は
　\(\displaystyle \hspace{4pt}5-\frac{10}{3}=\frac{5}{3}\)
\(\,y\,\)座標は同じで
　\(\,\mathrm{\displaystyle C\,\left(\frac{5}{3}\,,\,5\,\right)}\,\)

ここまでを書き込んでおきます。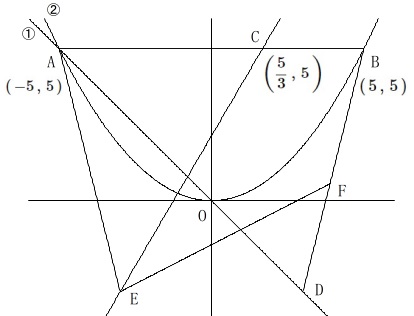次に、
条件から\(\,\mathrm{AO:OD=5:3}\,\)なので
（直線上だから\(\,x\,\)座標だけを考えてもいいので）
点\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,3\,\)で
\(\,①\,\)上の点なので点\(\,\mathrm{D}\,\)の座標
　\(\,\mathrm{D\,(\,3\,,\,-3\,)}\,\)

さらに点\(\,\mathrm{E}\,\)は点\(\,\mathrm{D}\,\)と\(\,y\,\)軸について対称なので
　\(\,\mathrm{E\,(\,-3\,,\,-3\,)}\,\)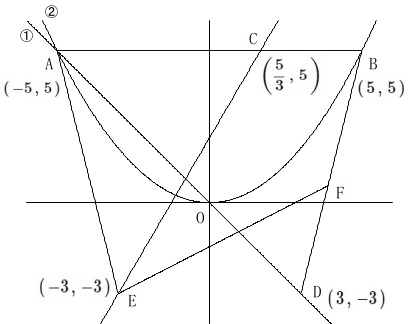ここまでは必ずやっておくべきことですよ。

本当ならすべての直線の式も出しておいた方が良いですが、
問題にあるので順に求めていきます。

\(\,(ア)\,\)
点\(\,\mathrm{A}\,\)や点\(\,\mathrm{B}\,\)は\(\,y=a\,x^2\,\)上の点なので
代入すれば比例定数が決まります。
ここでは点\(\,\mathrm{A}\,\)を通ることから求めます。

　\(\begin{eqnarray}\displaystyle
5&=&a\times (-5)^2\\
25\,a&=&5\\
a&=&\underline{　\frac{1}{5}　}
\end{eqnarray}\)

答え　\(\,4\,\)

\(\,(イ)\,\)
直線\(\,\mathrm{CE}\,\)の式を求めます。

\(\,(ⅰ)\,\)
傾き\(\,m\,\)を求めます。

２点
　\(\,\mathrm{\displaystyle C\,\left(\frac{5}{3}\,,\,5\,\right)}\,\)
　\(\,\mathrm{E\,(\,-3\,,\,-3\,)}\,\)
を通る直線は傾き\(\,m\,\)が
　\(\begin{eqnarray}\displaystyle
m&=&\frac{-3-5}{-3-\frac{5}{3}}\\
&=&\frac{-8}{-\frac{14}{3}}\\
&=&8\times \frac{3}{14}\\
&=&\underline{　\frac{12}{7}　}
\end{eqnarray}\)

答え　\(\,4\,\)

分数で割るというのを苦手にしている人が多いですが、
割り算は逆数の掛け算です。

\(\,(ⅱ)\,\)
直線の\(\,y\,\)切片\(\,n\,\)を求めます。

\(\,(ⅰ)\,\)で傾きが分かったので直線の式は
　\(\hspace{4pt}\displaystyle y=\frac{12}{7}\,x+n\)

これが\(\,\mathrm{E\,(\,-3\,,\,-3\,)}\,\)を通るので代入すると
　\(\begin{eqnarray}\displaystyle
-3&=&\frac{12}{7}\times (-3)+n\\
-3&=&-\frac{36}{7}+n\\
n&=&-3+\frac{36}{7}\\
&=&\frac{-21+36}{7}\\
&=&\underline{　\frac{15}{7}　}
\end{eqnarray}\)

答え　\(\,6\,\)

もちろん点\(\,\mathrm{C}\,\)の座標を代入しても良いです。

\(\,(ウ)\,\)
三角形\(\,\mathrm{AEC}\,\)と四角形\(\,\mathrm{BCEF}\,\)の面積が等しくなるときの
点\(\,\mathrm{F}\,\)の座標を求めます。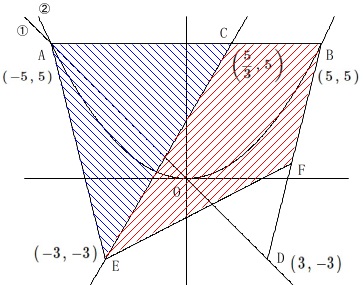具体的な面積計算が手っ取り早いでしょう。

条件から長さおよび高さが出ているので
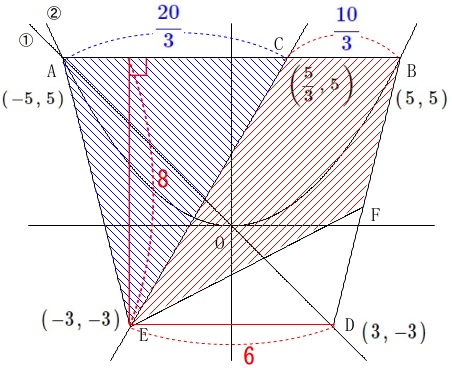　\(\begin{eqnarray}\displaystyle
\mathrm{△AEC}&=&\frac{1}{2}\times \frac{20}{3}\times 8\\
&=&\frac{80}{3}
\end{eqnarray}\)

四角形\(\,\mathrm{BCEF}\,\)の面積は台形\(\,\mathrm{BCED}\,\)から\(\,\mathrm{△DEF}\,\)を引いたものです。
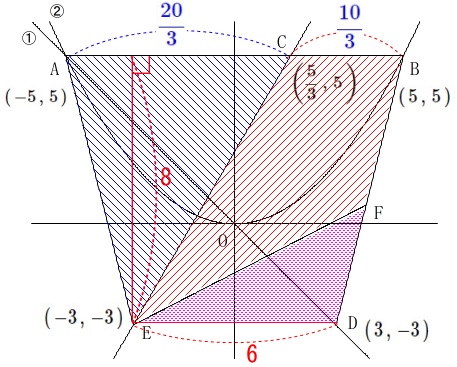台形\(\,\mathrm{BCED}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S_1&=&\frac{\frac{10}{3}+6}{2}\times 8\\
&=&\frac{28}{3}\times 4\\
&=&\frac{112}{3}
\end{eqnarray}\)

これらのことから
　\(\begin{eqnarray}\displaystyle
\mathrm{△FED}&=&\frac{112}{3}-\frac{80}{3}\\
&=&\frac{32}{3}
\end{eqnarray}\)
となるように\(\,\mathrm{F}\,\)を定めれば良いのです。

底辺を\(\,\mathrm{ED=6}\,\)とすると高さは
　\(\,\mathrm{F}\,\)の\(\,y\,\)座標と\(\,\mathrm{D}\,\)の\(\,y\,\)座標の差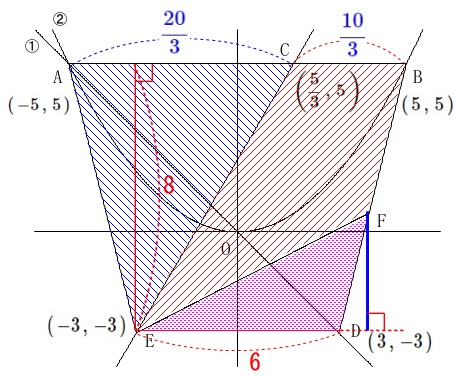なのでこれを\(\,\color{blue}{h}\,\)とすると
　\(\begin{eqnarray}\displaystyle
\mathrm{△FED}&=&\frac{1}{2}\times \mathrm{ED}\times h\\
\frac{32}{3}&=&\frac{1}{2}\times 6\times h\\
\color{blue}{h}&=&\frac{32}{3}\times \frac{1}{3}\\
&=&\color{blue}{\frac{32}{9}}
\end{eqnarray}\)

点\(\,\mathrm{D}\,\)の\(\,y\,\)座標は\(\,-3\,\)だから
点\(\,\mathrm{F}\,\)の\(\,y\,\)座標は
　\(\hspace{10pt}-3+\color{blue}{h}\\
\displaystyle =-3+\color{blue}{\frac{32}{9}}\\
\displaystyle =\frac{-27+32}{9}\\
\displaystyle =\frac{5}{9}\)

直線\(\,\mathrm{BD}\,\)の式は（自分で求めて下さい。）
　\(\hspace{10pt}y=4x-15\)
なのでこれに\(\,\mathrm{F}\,\)の\(\,y\,\)座標を代入すると
　\(\begin{eqnarray}\displaystyle
\frac{5}{9}&=&4x-15\\
4x&=&\frac{5}{9}+15\\
&=&\frac{140}{9}\\
x&=&\frac{35}{9}
\end{eqnarray}\)

よって点\(\,\mathrm{F}\,\)の座標は
　\(\displaystyle \underline{　\mathrm{F}\,\left(\,\frac{35}{9}\,,\,\frac{5}{9}\,\right)　}\)

（ウ）の比を利用した別解

\(\,(ウ)\,\)
比を使って点\(\,\mathrm{F}\,\)の座標を求めておきます。

直線\(\,\mathrm{BD}\,\)の式が必要になるのは同じです。
直線\(\,\mathrm{BD}\,\)の式は
　\(\hspace{4pt}y=4x-15\)

さて、
　\(\,\mathrm{△AEC}\,\)と四角形\(\,\mathrm{BCEF}\,\)の面積が等しい
とするなら
　\(\,\mathrm{AC:CB=2:1}\,\)
なので
　\(\,\mathrm{△AEC:△BCE=\color{magenta}{②}:\color{magenta}{①}}\,\)
です。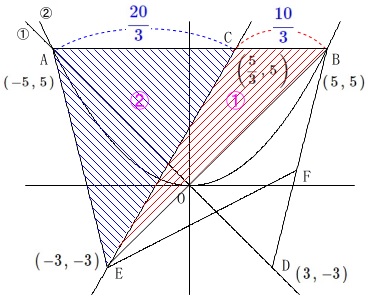このことから（\(\,\mathrm{△BCE}\,\)が\(\,\mathrm{△AEC}\,\)の半分だから）
　\(\,\mathrm{△BCE=△BEF}\,\)
となる点\(\,\mathrm{F}\,\)を定めれば良いことになります。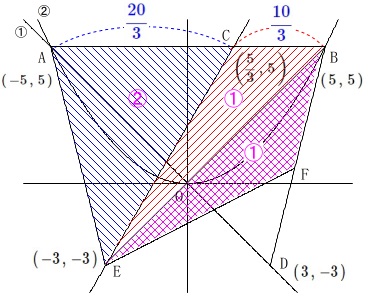ここで\(\,\mathrm{△BCE}\,\)と\(\,\mathrm{△BED}\,\)は高さが同じで
底辺の比が
　\(\begin{eqnarray}\displaystyle
\mathrm{BC:ED}&=&\frac{10}{3}:6\\
&=&5:9
\end{eqnarray}\)
なので
　\(\,\mathrm{△BCE:△BED=5:9}\,\)

\(\,\mathrm{△BCE=△BEF}\,\)となるには
点\(\,\mathrm{F}\,\)が\(\,\mathrm{BF:FD=5:4}\,\)を満たせば良いのです。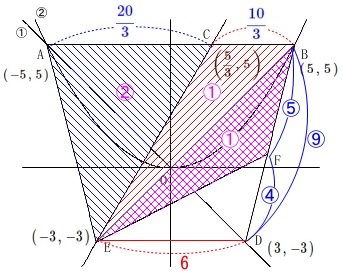点\(\,\mathrm{B}\,\)と点\(\,\mathrm{D}\,\)の\(\,y\,\)座標の差\(\,8\,\)から
点\(\,\mathrm{F}\,\)の\(\,y\,\)座標は
　\(\begin{eqnarray}\displaystyle
y&=&-3+\frac{4}{9}\times 8\\
&=&\frac{-27+32}{9}\\
&=&\frac{5}{9}
\end{eqnarray}\)

このとき点\(\,\mathrm{F}\,\)の\(\,x\,\)座標は
直線\(\,\mathrm{BD}\,\)の式から
　\(\begin{eqnarray}\displaystyle
\frac{5}{9}&=&4\,x-15\\
4x&=&\frac{5}{9}+15\\
x&=&\frac{35}{9}
\end{eqnarray}\)

よって点\(\,\mathrm{F}\,\)の座標は
　\(\displaystyle \,\mathrm{F\,\left(\,\frac{35}{9}\,,\,\frac{9}{5}\,\right)}\,\)

説明をずいぶん飛ばしましたが
　\(\,\mathrm{AC:CB=2:1}\,\)
という条件からは比を利用してこの手順で求めることもできます。
（会員は分からないところがあればお問い合わせ下さい。）

問５確率

ルールがややこしくみえる確率の問題です。

【操作１】および【操作２】がルールになります。
例があるのでいくつか試して見ると良いです。

ポイントはさいころの出目１～６は
箱\(\,\mathrm{P}\,\)から選ぶとき、
　「組み合わせは１つしかない」
と気がつくことです。

箱\(\,\mathrm{P}\,\)から箱\(\,\mathrm{Q}\,\)に移すカードは
　\(\,a=1\,\)のとき\(\color{black}{\fbox{1}}\)
　\(\,a=2\,\)のとき\(\color{black}{\fbox{2}}\)
　\(\,a=3\,\)のとき\(\color{black}{\fbox{1}\,,\,\fbox{2}}\)
　\(\,a=4\,\)のとき\(\color{black}{\fbox{4}}\)
　\(\,a=5\,\)のとき\(\color{black}{\fbox{1}\,,\,\fbox{4}}\)
　\(\,a=6\,\)のとき\(\color{black}{\fbox{2}\,,\,\fbox{4}}\)
この組み合わせ以外ありません。

確率なので樹形図で良いですが、
手を動かすことをしなければ見えにくい問題ですよ。

箱\(\,\mathrm{Q}\,\)には
\(\,a=1\,\)のとき
　\(\,\color{blue}{1}\,,\,3\,,\,5\,,\,6\,\)
\(\,a=2\,\)のとき
　\(\,\color{blue}{2}\,,\,3\,,\,5\,,\,6\,\)
\(\,a=3\,\)のとき
　\(\,\color{blue}{1}\,,\,\color{blue}{2}\,,\,3\,,\,5\,,\,6\,\)
\(\,a=4\,\)のとき
　\(\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\)
\(\,a=5\,\)のとき
　\(\,\color{blue}{1}\,,\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\)
\(\,a=6\,\)のとき
　\(\,\color{blue}{2}\,,\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\)

これがすべての場合です。

\(\,(ア)\,\)
箱\(\,\mathrm{R}\,\)に入ってるカードが\(\,4\,\)枚となる確率です。

つまり、小さいさいころの出目
　「\(\,b\,\)の約数が４つ」
箱\(\,\mathrm{Q}\,\)にある場合です。

\(\,b=1～6\,\)の中で約数が4つあるのは
　\(\hspace{4pt}b=6\)
だけで
　\(\,6\,\)の約数\(\,1\,,\,2\,,\,3\,,\,6\,\)
が箱\(\,\mathrm{Q}\,\)に入っているのは
　\(\,a=3\,\)のときだけ
なので求める確率は
　\(\displaystyle \underline{　\frac{1}{36}　}\)
※
分母になる\(\,a\,,\,b\,\)の組み合わせは３６通りで、
そのうち\(\,a=3\,,\,b=6\,\)のときだけ。

答え　\(\,1\,\)

\(\,(イ)\,\)で使うので\(\,b\,\)の約数を表しておきます。
　\(\begin{array}{|c|c|} \hline
b & 約数\\ \hline
1 & 1\\ \hline
2 & 1\,,\,2\\ \hline
3 & 1\,,\,3\\ \hline
4 & 1\,,\,2\,,\,4\\ \hline
5 & 1\,,\,5\\ \hline
6 & 1\,,\,2\,,\,3\,,\,6\\ \hline
\end{array}\)

\(\,(イ)\,\)
箱\(\,\mathrm{R}\,\)に入っているカードが１枚だけとなる確率です。

あれこれ考えるより、
調べつくした方が早いです。

箱\(\,\mathrm{R}\,\)に入るカードが１枚となるのは
\(\,a=1\,\)のとき
　\(\mathrm{Q}:\{\,\color{blue}{1}\,,\,3\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=1\,,\,2\,,\,4\)の３通り。

\(\,a=2\,\)のとき
　\(\mathrm{Q}:\{\,\color{blue}{2}\,,\,3\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=2\,,\,3\,,\,4\,,\,5\)の４通り。

\(\,a=3\,\)のとき
　\(\mathrm{Q}:\{\,\color{blue}{1}\,,\,\color{blue}{2}\,,\,3\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=1\)の１通りだけ。

\(\,a=4\,\)のとき
　\(\mathrm{Q}:\{\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=3\,,\,4\,,\,5\)の３通り。

\(\,a=5\,\)のとき
　\(\mathrm{Q}:\{\,\color{blue}{1}\,,\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=1\,,\,2\)の２通り。

\(\,a=6\,\)のとき
　\(\mathrm{Q}:\{\,\color{blue}{2}\,,\,3\,,\,\color{blue}{4}\,,\,5\,,\,6\,\}\)
この中に約数が１つとなるのは
　\(b=2\,,\,3\,,\,5\)の３通り。

合計で１６通りあるので求める確率は
　\(\displaystyle \frac{16}{36}=\underline{　\frac{4}{9}　}\)

\(\,a\,\)の出目による\(\,\mathrm{Q}\,\)のカードと\(\,b\,\)の約数を対応させますが、
試験中の限られた時間での処理は忙しかったでしょう。

箱\(\,\mathrm{Q}\,\)に入っているカードを書き出すだけでもかなり違いますよ。

問６立体図形と線分の長さの問題

円すいと側面での距離の問題です。

円すいの条件
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{AC=9}\,\)
　点\(\,\mathrm{D}\,\)は側面上で\(\,\mathrm{A\,,\,B}\,\)間の長さが最短になる線を
　２等分した点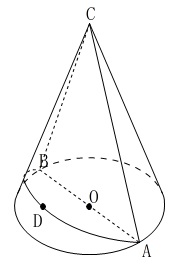
※
長さの単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。

\(\,(ア)\,\)
円すいの体積を求めます。

高さが必要になるので点\(\,\mathrm{C\,,\,A\,,\,B}\,\)を通る平面で切ります。
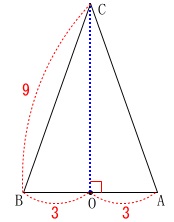断面は二等辺三角形で
\(\,\mathrm{AB=6}\,\)なので\(\,\mathrm{OB=3}\,\)です。

三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{OC^2+OB^2}&=&\mathrm{BC^2}\\
\mathrm{OC^2}+3^2&=&9^2\\
\mathrm{OC^2}&=&81-9\\
&=&72
\end{eqnarray}\)

\(\,\mathrm{OC}\,\)は長さだから\(\,\mathrm{OC\,＞\,0}\,\)より
　\(\hspace{10pt}\mathrm{OC}=6\sqrt{2}\)

底面の円の面積は
　\(\hspace{10pt}\pi\,(3)^2=9\,\pi\)

よって求める円すいの体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 9\,\pi\times 6\sqrt{2}\\
&=&\underline{　18\sqrt{2}\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

答え　\(\,2\,\)

\(\,(イ)\,\)
円すいの表面積を求めます。

円すいの展開図はおうぎ形と円です。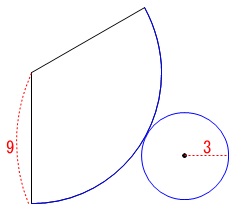底面の円周と扇形の弧の長さが等しくなります。

おうぎ形の面積は公式を使っても良いですが、
ここでは比例式で求めておきます。

半径\(\,9\,\)の円周は\(\,18\,\pi\,\)で
弧の長さが底面の円周\(\,\color{blue}{6\,\pi}\,\)なので
　\(\begin{eqnarray}\displaystyle
18\,\pi:6\,\pi&=&360:x\\
x&=&\frac{6\,\pi}{18\,\pi}\times 360\\
&=&120
\end{eqnarray}\)
なので中心角は\(\,\color{red}{120^{\circ}}\,\)です。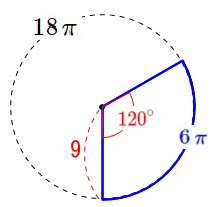このことから側面のおうぎ形の面積は
　\(\hspace{10pt}\displaystyle \pi\times (9)^2\times \frac{120}{360}\\
=27\,\pi\)

また底面の円の面積は\(\,9\,\pi\,\)なので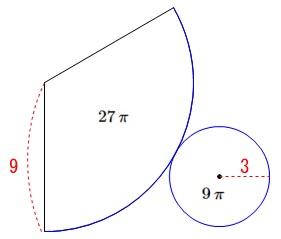求める表面積は
　\(\hspace{10pt}27\,\pi+9\,\pi\\
=\underline{　36\,\pi　}(\mathrm{cm^2})\)

側面のおうぎ形の面積は公式を使って
弧の長さが\(\,6\,\pi\,\)と分かった時点で
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\,\pi\times 9=27\,\pi\)
としても良いです。

表面積を求めるときは展開図です。

\(\,(ウ)\,\)
点\(\,\mathrm{D}\,\)から側面を一回りする長さが最も短くなるように線を引きます。
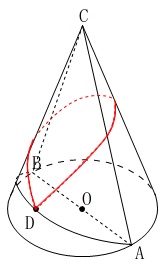位置関係が読み取りにくいので展開図で見てみると良いです。

点\(\,\mathrm{D}\,\)は\(\,\mathrm{AB}\,\)を２等分するので
線分（弦）\(\,\mathrm{AB}\,\)の中点になります。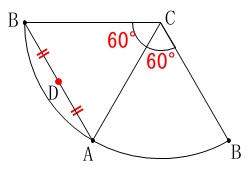この後は点\(\,\mathrm{D\,,\,C}\,\)を通る線分から\(\,120°\,\)のおうぎ形を書いても良いですが、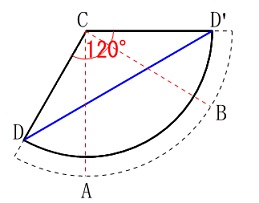もう一つ半径\(\,9\,\)のおうぎ形を足しても同じです。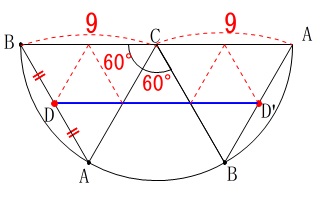線分\(\,\mathrm{DD’}\,\)が最も短くなります。

半円の直径が\(\,\mathrm{AB=18}\,\)なので
正三角形の性質を利用して
　\(\begin{eqnarray}\displaystyle
\mathrm{DD’}&=&\frac{3}{4}\times 18\\
&=&\underline{　\frac{27}{2}　}(\mathrm{cm})
\end{eqnarray}\)

問６（ウ）相似を使った別解

線分\(\,\mathrm{DC}\,\)の長さから相似を使って求めることもできます。

\(\,\mathrm{△BCD}\,\)は三角定規なので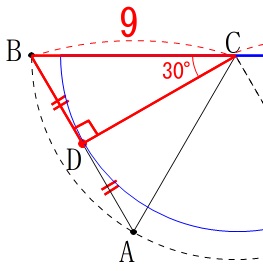
　\(\hspace{10pt}\displaystyle \mathrm{DC}=\color{blue}{\frac{9}{2}\sqrt{3}}\)
また下の図の\(\,\mathrm{EH}\,\)も同じ長さで
　\(\displaystyle \,\mathrm{EH}=\color{red}{\frac{9}{2}\sqrt{3}}\,\)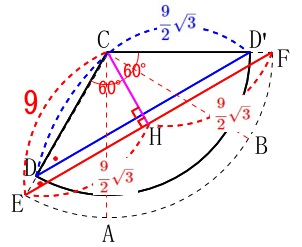ここで
　\(\,\mathrm{△DCD’}\,\)　∽　\(\,\mathrm{△ECF}\,\)
だから
　\(\begin{eqnarray}\displaystyle
\mathrm{EC:DC}&=&\mathrm{EF:DD’}\\
9:\frac{9}{2}\sqrt{3}&=&9\sqrt{3}:\mathrm{DD’}\\
9\times \mathrm{DD’}&=&\frac{9\times 9\times 3}{2}\\
\mathrm{DD’}&=&\frac{27}{2}
\end{eqnarray}\)