２０２１年度埼玉県公立高校入試数学【一般問題】の解説

２０２１年（令和３年）度の埼玉県公立高校入試数学の一般問題の解説です。
一部の単元項目を除く基本確認問題となりますので、
過去問対策としてではなく全体を通じて復習しておくと良いですね。
考え方は説明しますが別解などは示さずに問題の流れで解説していきます。

２０２１年度埼玉県公立高校入試の数学【一般】問題

試験での注意点と解答用紙は省いていますので、
埼玉県立高校受験予定の人は埼玉県のホームページで確認しておいてください。

⇒　2021埼玉県公立高校入試の数学【一般】問題

問題は\(\,\large{1}\,\)から\(\,\large{4}\,\)まであります。

２０２１年度埼玉県公立高校入試の数学【一般】問題の解説

解説ページなので対策を言うつもりはありませんが、
小問集合と呼んでも良い\(\,\large{1}\,\)と\(\,\large{2}\,\)だけで\(\,75\,\)点、
配点されていることは忘れないで下さい。

第１問の解説

\(\,\large{1}\,\)
小問が\(\,16\,\)題ありますので詳しい説明は省きます。

問題を解くときの基本を詳しく知りたい場合、
古い年度順に過去問解説を見ておいて下さい。

(1)
　\(\hspace{10pt}4x-9x\\
=\underline{　-5x　}\)

同類項をまとめるときは係数を計算します。

(2)
　\(\hspace{10pt}-3+(-4)\times 5\\
=-3-20\\
=\underline{　-23　}\)

足し算引き算より、掛け算割り算が先です。

(3)
　\(\hspace{10pt}4xy\div 8x\times 6y\\
\displaystyle =\frac{4xy\times 6y}{8x}\\
=\underline{　3y^2　}\)

分数線を１本で割り算の直後は分母に、
というより割り算は逆数の掛け算です。
　\(\hspace{10pt}4xy\div 8x\times 6y\\
\displaystyle =4xy\times \frac{1}{8x}\times 6y\\
=3y^2\)

(4)
　\(\begin{eqnarray}\displaystyle
3x+2&=&5x-6\\
3x-5x&=&-2-6\\
-2x&=&-8\\
x&=&\,\underline{　4　}\,
\end{eqnarray}\)

１次方程式を解くだけです。

(5)
　\(\hspace{10pt}\displaystyle 2\sqrt{3}-\frac{15}{\sqrt{3}}\\
\displaystyle =2\sqrt{3}-\frac{15\sqrt{3}}{3}\\
=2\sqrt{3}-5\sqrt{3}\\
=\,\underline{　-3\sqrt{3}　}\,\)

なれないうちは分母の有理化をていねいにやっておきましょう。
　\(\hspace{10pt}\displaystyle 2\sqrt{3}-\frac{15}{\sqrt{3}}\\
\displaystyle =2\sqrt{3}-\frac{15\times \color{red}{\sqrt{3}}}{\sqrt{3}\times \color{red}{\sqrt{3}}}\\
\displaystyle =2\sqrt{3}-\frac{15\sqrt{3}}{3}\\
=2\sqrt{3}-5\sqrt{3}\\
=\,\underline{　-3\sqrt{3}　}\,\)

配点が大きいこともありますし、
時間は十分あるので暗算はできるだけしない方が良いですよ。

(6)
二次式の因数分解です。

　\(\hspace{10pt}x^2\color{blue}{+7}x\color{red}{-18}\\
=\underline{　(x+9)(x-2)　}\)

かけて\(\,\color{red}{-18}\,\)、足して\(\,\color{blue}{7}\,\)になる組み合わせを探します。

(7)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 5x-4y=9\\
\hspace{4pt} 2x-3y=5
\end{cases}\)

ここでは\(\,y\,\)を消去していきます。
「両辺」を何倍かするのを忘れないようにしましょう。

　\(\hspace{14pt}15x-12y=27\\
\hspace{4pt}\underline{-)\hspace{4pt}8x-12y=20}\\
\hspace{18pt}7x\hspace{30pt}=7\\
\hspace{52pt}x=1\)

これをどれかの方程式に代入します。
（どれでも良いですよ。）
　\(\begin{eqnarray}\displaystyle
2\times (1)-3y&=&5\\
-3y&=&3\\
y&=&-1
\end{eqnarray}\)

答え　\(\,\underline{　x=1\,,\,y=-1　}\,\)

連立方程式を解くときの基本は、
どこまでいっても１文字消去です。

(8)
２次方程式を解きます。

　\(\hspace{4pt}2x^2-5x+1=0\)

因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-5)\pm \sqrt{(-5)^2-4\cdot 2\cdot 1}}{2\times 2}\\
&=&\frac{5\pm \sqrt{25-8}}{4}\\
&=&\underline{　\frac{5\pm \sqrt{17}}{4}　}
\end{eqnarray}\)

方程式を解くことと、
方程式の解を求めることは同じことです。

(9)
角度を求めます。

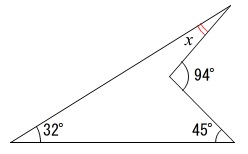
凹四角形なので公式もありますが、
補助線で求めておきます。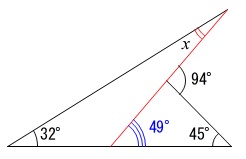辺を延長することで三角形をつくります。
　\(\begin{eqnarray}\displaystyle
x+32^{\circ}&=&49^{\circ}\\
x&=&\underline{　17^{\circ}　}
\end{eqnarray}\)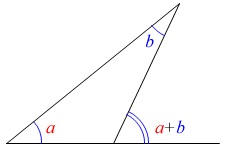三角形の外角と内角の関係を２回使ったことになります。

凹四角形の場合、　\(\hspace{4pt}d=a+b+c\)
となりますので覚えておいても良いです。

(10)
比例定数を求めます。

グラフを書いて確認する方が良いです。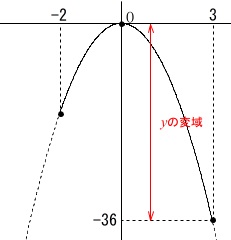　\(-36≦y≦0\)
の最小値\(\,y=-36\,\)は\(\,x=3\,\)のときです。

　\(\begin{eqnarray}\displaystyle
-36&=&a\times (3)^2\\
a&=&\underline{　-4　}
\end{eqnarray}\)

最大値\(\,0\,\)は\(\,x=0\,\)のときで、
\(\,x=-2\,\)のときの値は最大最小には関係ありません。

(11)
球体の体積や表面積の公式は、
中学生には求めることはできません。

半径\(\,r\,\)の球の体積\(\,V\,\)と表面積\(\,S\,\)は
　\(\hspace{4pt}\displaystyle V=\frac{4}{3}\,\pi\,r^3\)
　\(\hspace{4pt}\displaystyle S=4\,\pi\,r^2\)
覚えて使うしかない公式です。

半径が\(\,2\,\mathrm{cm}\)なので求める体積\(\,V\,\)と表面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{4}{3}\,\pi\,(2)^3\\
&=&\underline{　\frac{32}{3}\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
S&=&4\,\pi\,(2^2)\\
&=&\underline{　16\,\pi　}　(\mathrm{cm^2})
\end{eqnarray}\)

(12)
立方体の展開図問題です。

それぞれを組み立てて見取り図にしてしまえば良いですが、
対角線で考えると機械的に見ることができます。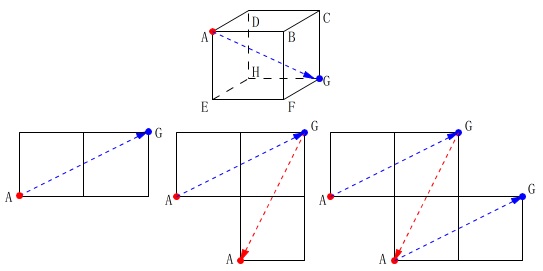展開図で隣り合う二マスでの移動が、
立方体の対角線の移動になり、
２回行うと元に戻ります。
（繰り返せばすべての点が分かります。）面\(\,\mathrm{A}\,\)の４点を対角線上に移動させると、
平行な面\(\,\mathrm{B}\,\)が分かります。

答え　\(\,\underline{　イ　}\,\)

(13)
有効数字のけた数を表す問題です。

⇒　有効数字とは？桁(けた)数と四捨五入の方法と表し方(中1資料)

別記事で詳しく説明しているので省略します。

　\(\hspace{4pt}12700=\color{black}{\fbox{　1.27　}}\times 10^\color{black}{\fbox{　4　}}\)

答え　ア　\(\,\underline{　1.27　}\,\)　イ　\(\,\underline{　4　}\,\)

(14)
さいころの出る目の確からしさです。

さいころは１回１回、１個１個の出かたは、
他のさいころの出目や回数に関係ありません。

答え　\(\,\underline{　エ　}\,\)

さいころを投げるとき、
３以下の目がでる確率と４以上の目が出る確率は
どちらも\(\,\displaystyle \frac{1}{2}\,\)です。

(15)
中央値と相対度数の問題です。

中央値になるのは\(\,40\,\)人のデータなので、
小さい順に並べたときの（大きい順でも同じ）、
　\(\,20\,\)番目と\(\,21\,\)番目の平均値
になります。

いずれも
　\(\,6\,\)時間以上\(\,8\,\)時間未満の階級
にあるので中央値が含まれる階級の度数は\(\,14\,\)
なので相対度数は度数合計で割って、
　\(\hspace{4pt}\displaystyle \frac{14}{40}=\underline{　0.35　}\)

代表値は小学生の内容に変わります。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

しかし、代表値の用語と意味は引き続き利用しますので確認しておきましょう。

(16)
曲線の長さの差を求めます。
※
「曲線」は「直線」を含む表現です。
問題では「ひもの長さの差」となっていますが、
解答の際は曲線と直線の意味を分けて書く必要があります。
アのひもの長さは、
半径\(\,2\,\)の円周\(\,4\,\pi\,\)と直線部分\(\,16\,\)の和であり、
　\(\hspace{4pt}4\,\pi+16　\mathrm{cm}\)
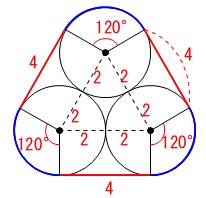イのひもの長さは、
半径\(\,2\,\)の円周\(\,4\,\pi\,\)と直線部分\(\,12\,\)の和であり、
　\(\hspace{4pt}4\,\pi+12　\mathrm{cm}\)
よって、ひもの長さの差は
　\(\hspace{10pt}(4\,\pi+16)-(4\,\pi+12)\\
=\underline{　4　}　\mathrm{cm}\)

「弧の部分の長さの和はア、イともに同じで、
直線部分の差がひもの長さの差になるので、
　\(\hspace{10pt}16-12=\underline{　4　}　\mathrm{cm}\)」
でも良いです。

第２問の解説

\(\,\large{2}\,\)
作図と座標上の面積の問題の２題です。

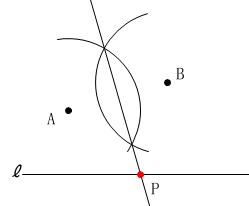
(1)
２点から等しい距離にある点の集まりは、
　「垂直二等分線」
なので２点\(\,\mathrm{A\,,\,B}\,\)の垂直二等分線と
直線\(\,\ell\,\)との交点が\(\,\mathrm{P}\,\)です。

(2)
関数の問題でもあり、面積の問題でもあります。

関数
　\(\hspace{4pt}y=2x^2\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-3\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,2\,\)
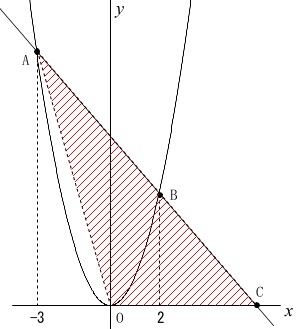このときの\(\,\mathrm{△AOC}\,\)の面積を求めます。

２点\(\,\mathrm{A\,,\,B}\,\)の座標は
　\(\,\mathrm{A\,(\,-3\,,\,18\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,8\,)}\,\)
となるので直線\(\,\ell\,\)の傾きは
　\(\hspace{4pt}\displaystyle \frac{8-(18)}{2-(-3)}=-2\)
直線\(\,\ell\,\)の式を
　\(\hspace{4pt}\displaystyle y=-2\,x+b\)
とおいて\(\,\mathrm{A}\,\)か\(\,\mathrm{B}\,\)の座標を代入して
（ここでは\(\,\mathrm{B}\,\)を代入します。）
　\(\begin{eqnarray}\displaystyle
8&=&-2\times (2)+b\\
b&=&12
\end{eqnarray}\)
直線\(\,\ell\,\)の式は
　\(\hspace{4pt}y=-2x+12\)

直線\(\,\ell\,\)の\(\,x\,\)軸との交点（\(\,x\,\)切片）は
直線\(\,\ell\,\)の\(\,y\,\)に\(\,y=0\,\)を代入して
（\(\,x\,\)軸は\(\,y=0\,\)という直線です。）
　\(\begin{eqnarray}\displaystyle
0&=&-2\,x+12\\
x&=&6
\end{eqnarray}\)
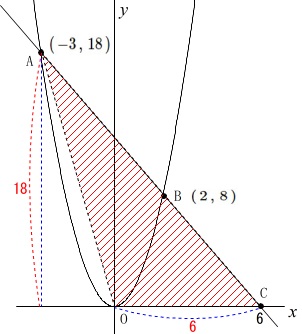よって求める\(\,\mathrm{△AOC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△AOC}&=&\frac{1}{2}\times 6\times 18\\
&=&\underline{　54　}　\mathrm{(cm^2)}
\end{eqnarray}\)

分かる座標はすべて書き込むことがポイントです。

第３問の解説

\(\,\large{3}\,\)
規則性と文字式による証明問題です。

(1)
(2)を証明するために具体的な自然数を入れますが、
直感でもいいのであてはめれば良いです。

　\(\hspace{4pt}1\,,\,5\,,\,9\,,\,\cdots\)

４ずつ増えているので次は\(\,13\,\)です。
　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　13　}\,\)

\(\,x=13\,\)のとき\(\,3x+5\,\)は
　\(\hspace{4pt}3\times (13)+5=44\)

　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　44　}\,\)

\(\,3x+5\,\)は\(\,3\,\)ずつ増えるので
　\(\begin{array}{|c|c|c|c|c|} \hline
x & 10 & 11 & 12 & \color{red}{13} \\ \hline
3x+5 & 35 & 38 & 41 & \color{red}{44} \\ \hline
\end{array}\)
としても良いです。

(2)
文字式を利用して(1)を一般化します。

（証明）
　\(\,n\,\)を\(\,0\,\)以上の整数とすると、
\(\,4\,\)で割ると\(\,1\,\)余る自然数は
　\(\,\color{red}{4\,n+1}　･･･\color{black}{\fbox{　①　}}\,\)
と表される。
このとき\(\,3x+5\,\)の\(\,x\,\)に
\(\hspace{4pt}x=4n+1\)を代入すると
　\(\hspace{10pt}3x+5\\
=3(4n+1)+5\\
=12n+8\\
=4(3n+2)\)
ここで\(\,3n+2\,\)は整数なので
これは\(\,4\,\)の倍数である。　･･･②
したがって、\(\cdots\)」

部分的にうめる証明なので書き進めにくかったかもしれませんが、
「\(\,3x+5\,\)が\(\,4\,\)の倍数になる。」
内容が（文字式で）伝われば良いです。

第４問の解説

\(\,\large{4}\,\)
相似の証明と線分の長さと面積を求める問題です。

全体に通じる条件を書き出しておきます。

条件
　\(\mathrm{∠ABC=∠ACD}\)
　\(\,\mathrm{CE}\,\)は\(\,\mathrm{∠BCD}\,\)の二等分線
　\(\,\mathrm{AD=4}\,\)
　\(\,\mathrm{AC=6}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。）

(1)
相似の証明です。
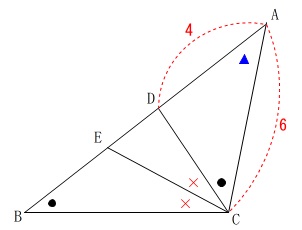　（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ACD}\,\)において
仮定から
　\(\,\mathrm{∠ABC=∠ACD　･･･①}\,\)
また、共通の角になっているので
　\(\,\mathrm{\color{blue}{∠BAC}=\color{blue}{∠CAD}　･･･②}\,\)
\(\,①②\,\)より
　２組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)
（終わり）

相似の証明は、
相似条件をそろえることと、
図の中で証明を終わらせておくことがポイントです。

(2)
線分の長さを求めます。

ここは求める経路は分かれると思うのですが、
条件に角の二等分線があるので定理を覚えましょう。

　\(\,\mathrm{∠BAC}\,\)の二等分線と対辺との交点\(\,\mathrm{P}\,\)において
　\(\,\mathrm{\color{red}{AB}:\color{blue}{AC}=\color{red}{BP}:\color{blue}{CP}}\,\)
内角の二等分線定理です。

この問題は別の経路が用意されているし、
平行線を引くことによって
この定理を使わなくても答えは出るようになっています。

しかし、
この定理を使う問題は多いので覚えてしまいましょう。
簡単な定理なので教科書に無くても使って良いです。

線分\(\,\mathrm{BE}\,\)の長さを求めましょう。

その前に、(1)の相似により分かることを追加します。
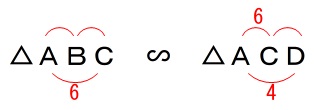　相似比は
　\(\hspace{4pt}\mathrm{AC:AD}=6:4=\color{magenta}{3}:\color{magenta}{2}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AC:AD}&=&\mathrm{AB:AC}\\
\color{magenta}{3}:\color{magenta}{2}&=&\mathrm{AB}:6\\
\mathrm{AB}&=&\color{blue}{9}
\end{eqnarray}\)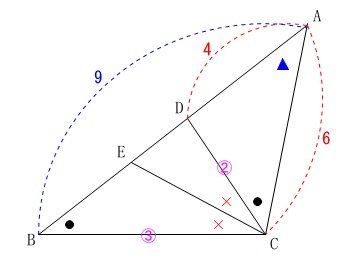このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{BD}&=&\mathrm{AB-AD}\\
&=&\color{blue}{9}-\color{red}{4}\\
&=&\color{magenta}{5}
\end{eqnarray}\)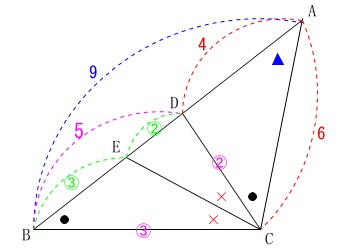\(\,\mathrm{CE}\,\)は\(\,\mathrm{∠BCD}\,\)の二等分線なので
角の二等分線定理により、
　\(\begin{eqnarray}\displaystyle
\mathrm{BE:DE}&=&\mathrm{BC:DC}\\
&=&③:②
\end{eqnarray}\)

よって、
　\(\hspace{10pt}\mathrm{BE}=\underline{　3　}　(\mathrm{cm})\)

※
線分\(\,\mathrm{BD}\,\)が\(\,\mathrm{5}\,\)なので\(\,\mathrm{BE=3}\,\)としましたが、
　\(\begin{eqnarray}\displaystyle
\mathrm{BE}&=&\frac{③}{③+②}\times \mathrm{BD}\\
&=&\frac{3}{5}\times 5\\
&=&3
\end{eqnarray}\)
のことです。

このとき\(\,\mathrm{DE=2}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AE}&=&\mathrm{AD+DE}\\
&=&4+2\\
&=&6\\
&=&\mathrm{AC}
\end{eqnarray}\)
となり\(\,\mathrm{△ACE}\,\)が二等辺三角形であることが分かります。

※
角の二等分線定理を使わない場合、
　\(\,\mathrm{∠ACE=∠AEC}\,\)
なので
　\(\,\mathrm{△ACE}\,\)が二等辺三角形
ということを先に見つけます。\(\,\large{1}\,\)の(9)を見直しておいて下さい。

それほど時間をかけるところでもないので先に行きます。

(3)
三角形の面積を求めます。

条件が加わりますので利用しましょう。

加わる条件
　線分\(\,\mathrm{AF}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線
　線分\(\,\mathrm{AF}\,\)と線分\(\,\mathrm{EC}\,\)の交点が\(\,\mathrm{G}\,\)
　\(\,\mathrm{△ABC}\,\)の面積は\(\,\mathrm{18cm^2}\,\)
このとき\(\,\mathrm{△GFC}\,\)の面積を求めます。

公式のない三角形の面積なので
　\(\,（全体）－（部分）\,\)
または
　\(\,（部分）＋（部分）\,\)
で求めます。　

ここまで来れば分かる面積を求め続ければ良いだけです。

線分\(\,\mathrm{AF}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線なので
　\(\hspace{4pt}\mathrm{BF:FC}=9:6=3:2\)『超え太郎』で学んだ人なら使いたくなる定理が出てきますが、
普通に二等辺三角形の定理と面積を使います。

　\(\,\mathrm{△ABC=18}\,\)
　\(\mathrm{BF:FC}=3:2\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△AFC}}&=&\frac{2}{5}\times \mathrm{△ABC}\\
&=&\frac{2}{5}\times 18\\
&=&\color{blue}{\frac{36}{5}}
\end{eqnarray}\)

二等辺三角形\(\,\mathrm{AEC}\,\)の面積は
　\(\hspace{4pt}\mathrm{AE:EB}=6:3=2:1\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△AEC}&=&\frac{2}{3}\times \mathrm{△ABC}\\
&=&\frac{2}{3}\times 18\\
&=&12
\end{eqnarray}\)

また\(\,\mathrm{△AGC}\,\)は\(\,\mathrm{△AEC}\,\)の半分なので
　\(\hspace{4pt}\mathrm{\color{magenta}{△AGC}}=\color{magenta}{6}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△GFC}&=&\mathrm{\color{blue}{△AFC}-\color{magenta}{△AGC}}\\
&=&\color{blue}{\frac{36}{5}}-\color{magenta}{6}\\
&=&\frac{36-30}{5}\\
&=&\underline{　\frac{6}{5}　}　(\mathrm{cm^2})
\end{eqnarray}\)

線分比だけでも答えは出ますが省略します。
※
学校選択問題の解説で簡単に説明します。

この問題でもそうですが解法は１つではありませんので、
分かることを書き出して進めてください。

２０２１年度の埼玉県立高校入試数学の一般問題は以上です。

⇒　埼玉県公立高校入試の数学（一般・学校選択問題）過去問と解説

２０２１年度は省かれている単元がありますが、
一般問題は例年、基本が広く問われています。