北海道公立入試2018年(平成30年)度裁量問題問5の問題と解説

北海道で2018年(平成30年度)に行われた公立入試の裁量問題問5の問題と解説です。
規則性、連立方程式、座標上の相似、錐体の性質の割と差のつく問題群となっていますが、基本通りやればたいしたことはありません。
裁量問題の問1から問4までは一般入試の問2から問5と全く同じなので省略します。

問題は北海道公式サイトにもあります。
北海道の問題は「過去問」として並べてくれているので探しやすかったです。笑

⇒　裁量問題

裁量問題で受験するという道立最高峰といえる高校志望の女の子を指導したことがありますが、
ひと月あまりで数学の得点率を40％程度から80％以上に上げ合格報告を頂きました。

北海道と九州でものすご～く遠いですが、メールだと一瞬で説明が届くので便利です。笑

そのとき徹底的に指導したことといえばポイントは数学のコツ一点でした。
ただ、それは現状を度々報告してくれていたからできたことで誰にでも共通することではありません。

ですのでここではこの年の裁量問題に、一般に通用する方法で解説しておきます。

裁量問題　\(\large{\color{black}{\fbox{ 5 }}}\)　の解説

小学生でもできる規則性の見抜き方

問題を読み始めるまでは3台のエレベーターが同時に動いているのかと思ったら違っていました。
例のごとく、エレベーターとか点検などの言葉を無くせば、単なる規則性と、連立方程式の問題ですね。

\(\,問1\,\)　\(\,\mathrm{A}\,\)が\(\,1\,\)階から\(\,n\,\)階まで上り\(\,1\,\)階まで降りてくる時間を\(\,n\,\)で表す問題です。

規則性の問題は他県でもよく出題されます。
普通なら誘導がついてくるのですが、裁量問題というだけあってついていません。

いきなり\(\,n\,\)で表すことになっています。
ただそれだけの違いなのでやることは同じですね。

\(\,1\,\)フロアーの上昇に\(\,\color{blue}{8}\,\)秒、各階に\(\,\color{red}{7}\,\)秒停止、を繰り返します。
最上階だけはこの停止\(\,\color{magenta}{7}\,\)秒だけで折り返す点に注意すれば

\(\,1\,\)階から\(\,2\,\)階まで上がって降りてきたとすると
　\(\,\color{blue}{8}+\color{magenta}{7}+\color{blue}{8}\,\)（秒）
かかります。

\(\,1\,\)階から\(\,3\,\)階まで上がって降りてきたとすると
　\(\,\color{blue}{8}+\color{red}{7}+\color{blue}{8}+\color{magenta}{7}+\color{blue}{8}+\color{red}{7}+\color{blue}{8}\,\)（秒）
かかります。

\(\,1\,\)階から\(\,4\,\)階まで上がって降りてきたとすると
　\(\,\color{blue}{8}+\color{red}{7}+\color{blue}{8}+\color{red}{7}+\color{blue}{8}+\color{magenta}{7}+\color{blue}{8}+\color{red}{7}+\color{blue}{8}+\color{red}{7}+\color{blue}{8}\,\)（秒）
かかります。

色違いの\(\,\color{magenta}{7}\,\)は上った階の最上階で止まっている時間です。
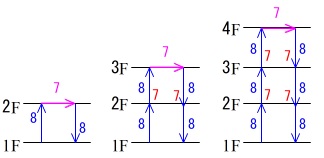これを見れば\(\,n\,\)階まで行くには？
と裁量問題で受験しようとしている人にはたやすいでしょう。
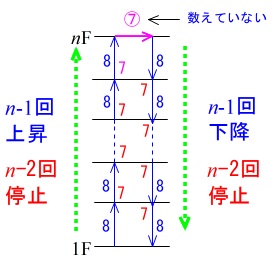最上階で止まっている\(\,\color{magenta}{7}\,\)秒を別に考えて、
往復分の時間と最上階で止まっている時間を加えて

　\(\hspace{10pt}\color{blue}{8(n-1)}\times 2 + \color{red}{7(n-2)}\times 2+\color{magenta}{7}\\
=16(n-1)+14(n-2)+7\\
=16n-16+14n-28+7\\
=30n-44+7\\
=\underline{30n-37}\)

なぜ\(\,3≦n≦10\,\)と限定しているのかですが、分かりません。

連立方程式を立てる前に確認しておくこと

問題に
　\(\,x\,,\,y\,\)として方程式を作り求めなさい。
とあるので文字2つの連立方程式を立てるというのはわかりますが、
文章題で大切なのは、

　\(\,x\,は\,\mathrm{\color{red}{B}}\,が\,1\,つ階を移動すのにかかる時間\,\)
　\(\,y\,は\,\mathrm{\color{blue}{C}}\,が\,1\,つ階を移動するのにかかる時間\,\)

という文字の内容をしっかり理解しておくことです。

　・\(\,\mathrm{\color{red}{B}}\,\)は\(\,1\,\)階から\(\,10\,\)階まで各階止まりで、
　各階で\(\,7\,\)秒止まって上昇します。

　・\(\,\mathrm{\color{blue}{C}}\,\)は\(\,10\,\)階からノンストップで\(\,1\,\)階まで下降し、
　\(\,1\,\)階で\(\,11\,\)秒止まってノンストップで\(\,10\,\)階まで上昇します。

　・\(\,\mathrm{\color{red}{B}}\,\)の方が\(\,1\,\)つ階を上昇するのに\(\,\mathrm{\color{blue}{C}}\,\)より\(\,2\,\)秒多くかかる。

　・同時に動き出し、同時に\(\,10\,\)階に着いた。

という条件です。
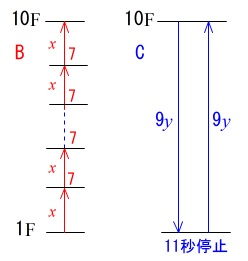まずは
　「\(\,\mathrm{\color{red}{B}}\,\)の方が\(\,1\,\)つ階を上昇するのに\(\,\mathrm{\color{blue}{C}}\,\)より\(\,2\,\)秒多くかかる。」
から
　
　\(\,x=y+2　･･･①\,\)

\(\,\mathrm{\color{red}{B}}\,\)が\(\,10\,\)階まで上昇するのにかかった時間は

　\(\color{red}{\,9\,回の上昇}と\,\color{red}{8\,回の停止}\,\)

なので

　\(\,9x+7\times 8\,\)

\(\,\mathrm{\color{blue}{C}}\,\)が\(\,10\,\)階から\(\,10\,\)階まで往復するのにかかった時間は

　\(\,9y\times 2+11\,\)

これらが同時に10階に着いたので

　\(\,9x+7\times 8=9y\times 2+11　･･･②\,\)

①②から
　\(\,\underline{x=9\,,\,y=7}\,\)

これくらいの連立方程式が処理できないなら、
裁量問題はあきらめた方が良いレベルなので計算は省略しました。笑

座標上での点と面積の求め方

問2　座標を求める問題です。

当然ですが問題に与えられた条件を座標上に図示します。
これをやらない人は解く気はないと見なされるし、裁量問題には挑戦しない方が良いです。
受けるのは自由ですが、ほとんどの人は撃沈しますよ。
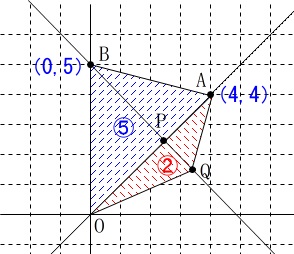これが全体に通じる条件です。
点\(\,\mathrm{P}\,\)は固定された点ではないので、\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)は動きます。

面積比が\(5:2\)なので\(\,\mathrm{OA}\,\)を2つの三角形の底辺だと見れば、
高さの比は\(\,\mathrm{BP:PQ}\,\)であることは見ておいてください。

(1)点\(\,\mathrm{P}\,\)が原点にあるときの\(\,\mathrm{Q}\,\)の座標を求める問題です。
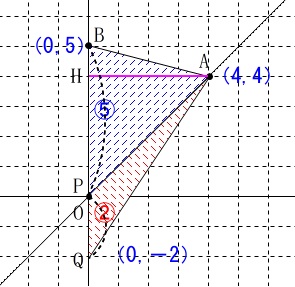2つの三角形は\(\,\mathrm{\color{magenta}{AH}}\,\)を共通の高さにしているので、
底辺となる\(\,\mathrm{BP}\,\)と\(\,\mathrm{PQ}\,\)が

　\(\,\mathrm{BP:PQ}=5:2\,\)

のとき面積比も\(\,5:2\,\)になります。
だから
　点\(\,\mathrm{Q}　\underline{(\,0\,,\,-2\,)}\,\)

このときは長さを直接出したかったので底辺を\(\,\mathrm{OA}\,\)で見ていません。

ここまでは問題を読んで図示すれば簡単に出てきます。
次は点\(\,\mathrm{P}\,\)を動かしたときの線分\(\,\mathrm{PQ}\,\)の動く面積です。
この
　線分が動いてできる面積
というのを見慣れていないかもしれません。

これは、その線分が動いたときに塗りつぶす面積のことです。

問2　線分\(\,\mathrm{PQ}\,\)が動いてできる図形の面積を求めます。

これは点\(\,\mathrm{P}\,\)が動くと\(\,\mathrm{Q}\,\)も同時に動くので、
\(\,\mathrm{PQ}\,\)が動いて塗りつぶす範囲の面積になります。

\(\,\mathrm{P}\,\)は\(\,\mathrm{O}\,\)から\(\,\mathrm{A}\,\)まで動くのでいくつか書き込んでいくと見えてきます。
この作業は自分でやらないと、この問題は良いですけど、他の問題のときを解くときに自分ではできないままですよ。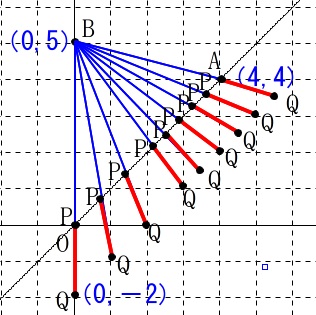\(\,\mathrm{Q}\,\)が動く点をつなげてみると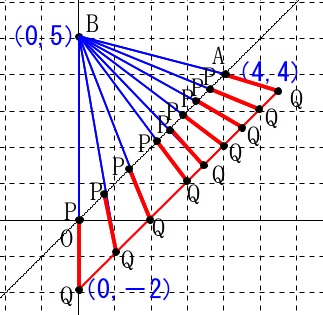\(\,\mathrm{PQ}\,\)が塗りつぶす範囲も見えてきました。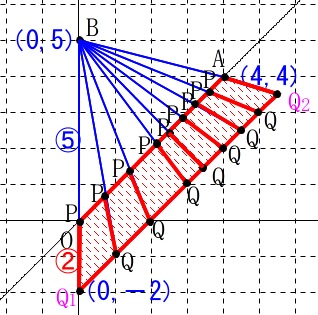\(\,\mathrm{PQ}\,\)が動いてできる図形は台形です。

\(\,\mathrm{△OAB:△OAQ=5:2}\,\)で底辺\(\,\mathrm{OA}\,\)を共通にしているから

　\(\,\mathrm{BP:PQ=5:2}\,\)

は常に成り立っているので、

　\(\,\mathrm{△BOA}\,\)　∽　\(\,\mathrm{△BQ_1Q_2}\,\)

　相似比は　\(\,5:7\,\)

　面積比は　\(\,\mathrm{5^2:7^2=25:49}\,\)

これから\(\,\mathrm{△BOA}\,\)と台形\(\,\mathrm{OQ_1Q_2A}\,\)の面積比は

　\(\,25:(49-25)=\color{red}{25:24}\,\)

\(\,\mathrm{△BOA}\,\)の面積は

　\(\begin{eqnarray}
　\displaystyle \mathrm{△BOA}&=&\mathrm{\frac{1}{2}\times BO\times AH}\\
&=&\frac{1}{2}\times 5\times 4\\
&=&10
\end{eqnarray}\)

なので\(\,\mathrm{PQ}\,\)が動いてできる図形の面積は

　\(\begin{eqnarray}
　台形\mathrm{OQ_1Q_2A}&=&\frac{24}{25}\times 10\\
&=&\underline{\frac{48}{5}}
\end{eqnarray}\)

自分で計算すればこの計算は回りくどく感じるでしょう。
好きなように計算して良いですよ。

図形問題だと見れば単なる相似の面積比を出して、基準の面積をかければ良いだけです。

計算大好きで\(\,\mathrm{BQ_2}\,\)の長さを出して三角形\(\,\mathrm{△BQ_1Q_2}\,\)の面積を出して、、、
とするのも良いですが時間がかかりすぎますよ。

錐体の高さと錐体の性質

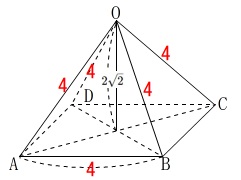
問3は正四角錐を転がしますが、四角錐の元の形を思い出せば割とすんなり進みます。

(1)これは四角錐の高さが与えられているので簡単です。
高さを聞かれることも多いですが、同じことです。

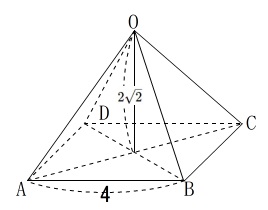
立体で長さを求めたければその線分を含む面を抜き出して考えると良いです。

\(\,\mathrm{OB}\,\)を含んでいる面は\(\,\mathrm{△ODB}\,\)です。
\(\,\mathrm{△OAB\,,\,△OBC}\,\)では長さが分かっているのは\(\,\mathrm{AB\,,\,BC}\,\)だけなので\(\,\mathrm{OB}\,\)は出てきません。
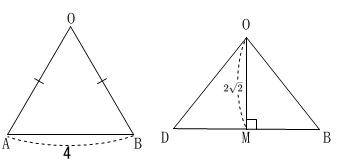\(\,\mathrm{△ODB}\,\)も\(\,1\,\)辺しか分かっていませんが、
底面\(\,\mathrm{ABCD}\,\)が正方形ということから\(\,\mathrm{DB}\,\)が求まります。

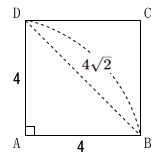
　\(\begin{eqnarray}
\mathrm{BD^2}&=&\mathrm{AB^2+AD^2}\\
&=&4^2+4^2\\
&=&32\\
&=&\pm 4\sqrt{2}\\
\mathrm{BD}&=&\sqrt4\sqrt{2}　（\mathrm{BD}＞0）
\end{eqnarray}\)

\(\,\mathrm{△ODB}\,\)に戻すと、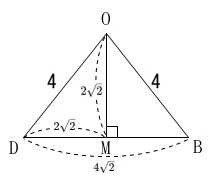三平方の定理から（直角二等辺三角形でもある）

　\(\,\mathrm{OB=\underline{4}}\,\)

もちろん正四角錐なので

　\(\,\mathrm{OA=OB=OC=OD=4}\,\)
ここまでは\(\,1\,\)分もあれば出せるでしょう。

考え方で変わってくるのはこれからです。
まずはありきたりな考え方で解いてみます。

(2)四角錐を転がしたときの高さ\(\,\mathrm{AH}\,\)を求めよ、という問題です。

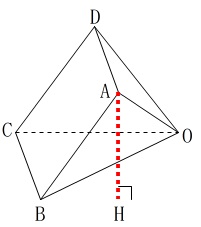錐体であろうが同じ立体を転がしただけなので体積は変わっていません。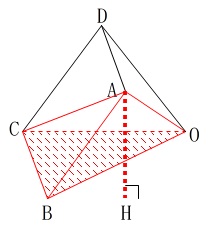底面を\(\,\mathrm{△OBC}\,\)、高さを\(\,\mathrm{AH}\,\)とする三角錐を考えると、
この錐体\(\,\mathrm{A-OBC}\,\)\(\,\color{red}{2つ分}\,\)が四角錐\(\,\mathrm{O-ABCD}\,\)の体積になっています。
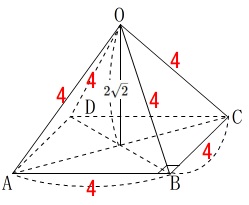四角錐\(\,\mathrm{O-ABCD}\,\)の体積は
　
　\(\hspace{10pt}(四角錐\,\mathrm{O-ABCD}\,の体積)\\
\displaystyle =\frac{1}{3}\times 底面積 \times 高さ\\
\displaystyle =\frac{1}{3}\times 4^2\times 2\sqrt{2}\\
\displaystyle =\frac{32\sqrt{2}}{3}\)

\(\,\mathrm{△OBC}\,\)の面積は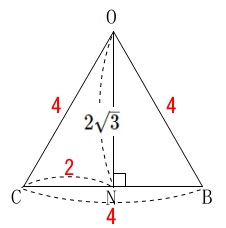正三角形なので

　\(\begin{eqnarray}
\displaystyle \mathrm{△OBC}&=&\frac{1}{2}\times \mathrm{BC} \times \mathrm{ON}\\
&=&\frac{1}{2}\times 4\times 2\sqrt{3}\\
&=&4\sqrt{3}
\end{eqnarray}\)

よって三角錐\(\,\mathrm{A-OBC}\,\)の体積は高さ\(\,\mathrm{AH}\,\)として

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times \mathrm{△OBC} \times \mathrm{AH}\\
\displaystyle =\frac{1}{3}\times 4\sqrt{3}\times \mathrm{AH}\)　

四角錐\(\,\mathrm{O-ABCD}\,\)の体積はこの三角錐\(\,\mathrm{A-OBC}\,\)の体積の2倍に等しいので

　\(\begin{eqnarray}
\displaystyle \frac{1}{3}\times 4\sqrt{3}\times \mathrm{AH}\times 2&=&\frac{32\sqrt{2}}{3}\\
\frac{8\sqrt{3}}{3}\times \mathrm{AH}&=&\frac{32\sqrt{2}}{3}\\
\mathrm{AH}&=&\frac{32\sqrt{2}}{3}\times \frac{3}{8\sqrt{3}}\\
&=&\frac{4\sqrt{2}}{\sqrt{3}}\\
&=&\underline{\frac{4\sqrt{6}}{3}}
\end{eqnarray}\)

このように見方を変えて高さを求めることは面積でもよくあります。
面積も体積も転がしただけでは変わらない、ということです。

これでいいと思いますが、錐体の元を考える、という超え太郎マスターは別の解法も思いついたかもしれないのでちょこっと説明しておきます。

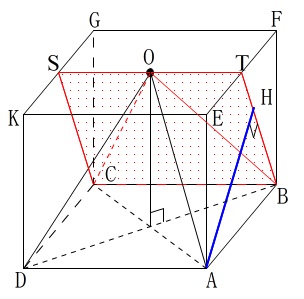この\(\,\mathrm{AH}\,\)を求めることと同じです。
台形\(\,\mathrm{ABTE}\,\)を抜き出すと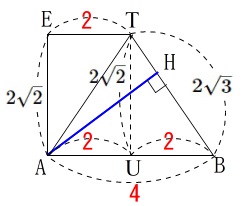\(\,\mathrm{△TAB}\,\)について面積を見ると、
底辺を\(\,\mathrm{AB}\,\)、高さを\(\,\mathrm{TU}\,\)と見る場合と、
底辺を\(\,\mathrm{TB}\,\)、高さを\(\,\mathrm{AH}\,\)と見る場合で面積は変わらないので、

　\(\begin{eqnarray}
\displaystyle \frac{1}{2}\times \mathrm{AB}\times \mathrm{TU}&=&\frac{1}{2}\times \mathrm{TB}\times \mathrm{\color{blue}{AH}}\\
\frac{1}{2}\times 4\times 2\sqrt{2}&=&\frac{1}{2}\times 2\sqrt{3}\times \mathrm{\color{blue}{AH}}\\
\mathrm{\color{blue}{AH}}&=&\frac{4\times 2\sqrt{2}}{2\sqrt{3}}\\
&=&\underline{\frac{4\sqrt{6}}{3}}
\end{eqnarray}\)

他にも相似を利用する方法もありますが、やめておきます。
長くなりすぎました。笑

学校や塾で教えてもらってください。

ここでは裁量問題攻略までにどれくらいの作業が必要かの分量を知ってもらえれば十分です。

北海道の公立入試では、一般と裁量問題との平均点の差がないから、、、という分析をしているところもあるようですが、
ちょっと違いますよ。

裁量問題で受験する人はそれなりの力を持っているということですから。

とはいえ、裁量問題の得点率は低いので差をつけることができてうれしくなる問題です。
一般の人には悪いけど差をつけさせて頂きます。笑

⇒　数学の成績を短期で飛躍させる

差をつけるか、つけられるかはあなた次第ですよ。

⇒　北海道の公立高校入試数学の過去問と解説

北海道の一般入試の解説もまとめておきました。