埼玉県公立高校入試2018学校選択問題の数学の問題と解説

埼玉県で2018年(平成30年)度に行われた公立高校入試問題のうち学校選択問題の数学の問題と解説です。
一般入試問題と重なる問題もありますので長くなりますが最後まで一気に行きます。
学校選択ということで少し問題量と計算量は増えますが基本的な方針は変えなくて良いです。

選択問題を選んでいる時点である程度は力はあるものとして簡単に済ませたいのですが、
最後まで簡単に済ませられる人は一部の人だけだと思うのでできるだけ解説を入れます。

問題を見て、手を動かしながら進めた方が力になりますよ。

⇒　2018埼玉県学校選択問題

一般入試問題と同じ問題がありますのでここでは同じ説明はしません。
問題が進んだ時点で解説先をお伝えします。

⇒　019年度埼玉県公立高校入試学校選択問題の数学の問題と解説

2019年度の学校選択問題の解説を更新しました。

文字式の計算と方程式と変域問題

　\(\,\Large{1}\,\)　は(1)～(9)まであります。

ただし、(5)と(7)～(9)までは一般入試と同じなので説明済みです。

(1)分数が混じった文字式の計算です。

分数の計算は文字を含んでいようがいまいがすべて同じです。
分母を1つにして分子の計算に集中すると計算ミスは減ります。

『覚え太郎』会員は逆に、普通の人はどうやって計算しているのか分からなくなっているのではないですか？笑

　\(\hspace{10pt}\displaystyle x+y-\frac{x-y}{6}\\
\displaystyle =\frac{6(x+y)-(x-y)}{6}\\
\displaystyle =\frac{6x+6y-x+y}{6}\\
\displaystyle =\underline{\frac{5x+7y}{6}}\)

この程度の計算で説明を入れる必要はないと思いますが、
分子には（かっこ）がついているということは忘れないようにしましょう。

　\(\hspace{10pt}\displaystyle x+y-\frac{x-y}{6}\\
\displaystyle =x+y-\frac{1}{6}x+\frac{1}{6}y\\
\displaystyle =\underline{\frac{5x+7y}{6}}\)

この程度の計算ができれば良いのなら分数係数の足し算でも良いでしょう。

(2)条件式よりも与式、求値式の変形が先ですね。

　\(\hspace{10pt}\displaystyle \frac{y}{x}-\frac{x}{y}\\
\displaystyle =\frac{y^2-x^2}{xy}\\
\displaystyle =\frac{(y+x)(y-x)}{xy}　･･･①\)

これは交代式なので2行目を見た時点で

　\(x+y\,,\,xy\,,\,x-y\)

を出しておくと計算が楽になると分かるので因数分解まで進めました。
変形した与式の因数と\(\,x,y\,\)の順序が違いますが結果は同じです。
ここでは与式の通り条件式から計算しておきます。

　\(\begin{eqnarray}
y+x&=&(\sqrt{3}-\sqrt{2})+(\sqrt{3}+\sqrt{2})\\
&=&\color{red}{2\sqrt{3}}
\end{eqnarray}\)

　\(\begin{eqnarray}
xy&=&(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})\\
&=&3-2=\color{blue}{1}
\end{eqnarray}\)

　\(\begin{eqnarray}
y-x&=&(\sqrt{3}-\sqrt{2})-(\sqrt{3}+\sqrt{2})\\
&=&\color{magenta}{-2\sqrt{2}}
\end{eqnarray}\)

これらを①に代入して

　\(\begin{eqnarray}
\displaystyle ①&=&\frac{(y+x)(y-x)}{xy}\\
&=&\frac{\color{red}{2\sqrt{3}}\times (\color{magenta}{-2\sqrt{2}})}{\color{blue}{1}}\\
&=&\underline{-4\sqrt{6}}
\end{eqnarray}\)

最初から\(x,y\)を代入して有理化してもたいした計算ではありません。

　\(\hspace{10pt}\displaystyle \frac{y}{x}-\frac{x}{y}\\
\displaystyle =\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}-\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\\
\displaystyle =\frac{(\sqrt{3}-\sqrt{2})(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}-\frac{(\sqrt{3}+\sqrt{2})(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}\\
\displaystyle =\frac{3-2\sqrt{6}+2}{3-2}-\frac{3+2\sqrt{6}+2}{3-2}\\
=(5-2\sqrt{6})-(5+2\sqrt{6})\\
=5-2\sqrt{6}-5-2\sqrt{6}\\
=\underline{-4\sqrt{6}}\)

この程度なら直接代入しても変わりませんね。

(3)2次方程式ですが\(\,x^2\,\)の係数が\(\,1\,\)ではなく、共通因数もないので解の公式利用だと分かります。
ただ、\(\,\color{red}{x-1}\,\)を「まとまり」として処理するか、展開するかですが、
どっちでも良いので迷っているより処理した方がはやいです。

両方やっておきます。

　\(\,x-1=A\,\)
とおくと
　\(3A^2-A-1=0\)
これから
　\(\begin{eqnarray}\displaystyle
A&=&\frac{-(-1)\pm \sqrt{(-1)^2-4\times 3\times (-1)}}{2\times 3}\\
&=&\frac{1\pm \sqrt{1+12}}{6}\\
&=&\frac{1\pm \sqrt{13}}{6}
\end{eqnarray}\)

\(\,A\,\)に\(\,x-1\,\)を戻すと

　\(\begin{eqnarray}\displaystyle
x-1&=&\frac{1\pm \sqrt{13}}{6}\\
x&=&1+\frac{1\pm \sqrt{13}}{6}\\
&=&\frac{6+1\pm \sqrt{13}}{6}\\
&=&\underline{　\frac{7\pm \sqrt{13}}{6}　}
\end{eqnarray}\)

次は展開して解の公式を使ってみます。

　\(\begin{eqnarray}
3(x-1)^2-(x-1)-1&=&0\\
3(x^2-2x+1)-(x-1)-1&=&0\\
3x^2-6x+3-x+1-1&=&0\\
3x^2-7x+3&=&0
\end{eqnarray}\)

解の公式から

　\(\begin{eqnarray}\displaystyle
x&=&\frac{7\pm \sqrt{(7)^2-4\times 3\times 3}}{2\times 3}\\
&=&\frac{7\pm \sqrt{49-36}}{6}\\
&=&\underline{　\frac{7\pm \sqrt{13}}{6}　}
\end{eqnarray}\)

置換するのに少し手間がいるなあ、というくらいの違いなので、
迷わず突っ走った方が結果までははやいでしょう。

ただ、「ちょっと考えてみた」というのは非常に良い感じです。
高校に進学してから大きな差になります。

(4)教科書によくある変域問題です。
\(\,y\,\)の変域を値域といいますので、値域という言葉を使って説明します。

関数問題で値域を聞かれることはよくあります。
このとき関数をながめて手を止めている人が多いですが、グラフを書きながら考えた方が良いですよ。
\(\,1\,\)次関数のように一定で変化する関数ばかりではありませんからね。

問題は簡単です。
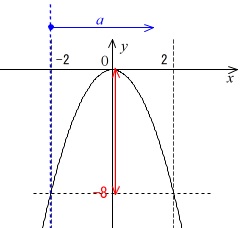値域は\(\,y\,\)が動ける範囲です。
　\(-8≦y≦0\)　となる\(\,x\,\)の範囲を探せば良いだけです。

値域の最大値が\(\,0\,\)だから\(\,a\,\)は\(\,0\,\)以上だと分かりますが、上限はいくらでも大きくはなりません。
放物線は軸で対称です。
　\(\,x=-2\,のときに,y=-8\,\)
なので
　\(\,x=2\,のときのも\,y=-8\,\)
を超えると最小値が\(\,-8\,\)より小さくなってしまいます。

グラフから読み取れば十分です。

　\(\,\underline{0≦a≦2}\,\)

(5)(9)は一般入試1-(10)(11)と同じ問題です。
詳しい説明は別のところにしてありますが、度数分布表の読みとりだけでなく資料の整理は用語の意味が分かっていなければ\(0\)点です。
食塩水の問題は比例の関係さえ理解していればすんなり終わる問題です。

⇒　埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策

自然数と除法と公倍数の問題

(6)あまりを考える整数問題です。

手を動かしていろいろと試して欲しいところですが、よくある問題なのでとっとと済ませます。

　ある自然数を\(\,N\,\)とします。

\(\,k\,,\,l\,,\,m\,\)を\(\,0\,\)以上の整数として

\(\,\color{red}{4で割ると3余る}\,\)から
　\(\,N=4k+3\,\)　

\(\,\color{red}{5で割ると4余る}\,\)から
　\(\,N=5\ell+4\,\)

\(\,\color{red}{6で割ると5余る}\,\)から
　\(\,N=6m+5\,\)

と書けるのですがよく見ると、
すべてあまりに\(\,+1\,\)すれば割り切れることになるので、

　\(\,\color{blue}{N+1\,は\,4\,と\,5\,と\,6\,の公倍数}\,\)

です。

「最も小さい数」なので最小公倍数\(\,\color{blue}{60}\,\)です。

　\(\,N+1=60\,\) 　だから　\(\,N=\underline{59}\,\)

割り算の商と余りの原理を忘れていたら整数問題はなかなか解けませんね。

ところがこの問題、小学生でも解けます。

\(\,\color{red}{4で割ると3余る}\,\)から
　\(\,N=3\,,\,7\,,\,11\,,\,15\,,\,19\,,\,23\,,\,\cdots\,\)　

\(\,\color{red}{5で割ると4余る}\,\)から
　\(\,N=4\,,\,9\,,\,14\,,\,19\,,\,24\,,\,29\,,\,\cdots\,\)

\(\,\color{red}{6で割ると5余る}\,\)から
　\(\,N=5\,,\,11\,,\,17\,,\,23\,,\,29\,,\,35\,,\,\cdots\,\)

と書き出していって、最初に共通した数字が求める最も小さい自然数です。
試験時間が長いとはいえないでしょうから調べて行くというのはなかなかできないですが、
考えている間に答えが出ているかもしれませんよ。

⇒　『短期間で中学数学の基礎からやり直す

(7)(8)は一般入試2-(1)(2)と同じです。

⇒　埼玉県立高校入試(2018過去問) 確率と図形問題の解説とポイント

　\(\large{1}\)　はここまでです。

円錐の側面と最短距離のよくある問題

　\(\large{2}\)
(1)作図問題ですが一般入試の2-(3)と同じです。

⇒　埼玉県立高校入試(2018過去問) 確率と図形問題の解説とポイント

(2)円錐の側面を最短距離で結ぶというのは中1でよく見かける問題です。
数学で距離というのは最短距離を意味するので直線になったときというのはわかるでしょう。

条件を図示して考えますが立体は立体のまま考えない、というのを基本にしておくと簡単になるんですよね。

学校選択問題を選択している埼玉県の受験生で、
円錐の側面を立体のままイメージする人もいないでしょう。

展開図を書くところ（書いたところ）から説明します。
円錐の展開図は、側面の扇形と底面の円からできています。
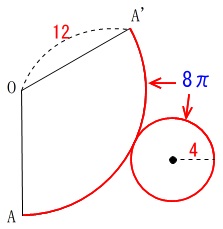ここまでは皆同じ作業になると思われます。
扇形の弧と底面の円の周が同じ、ということです。

\(\,\mathrm{OA}\,\)と\(\,\mathrm{OA’}\,\)は円錐に戻すと重なる辺です。
\(\,\mathrm{M}\,\)は\(\,\mathrm{OA}\,\)上の点ですが\(\,\mathrm{OA’}\,\)上の中点として見れば良いのです。
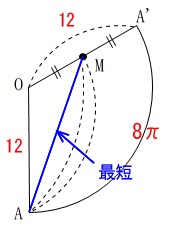後はさっさとこの\(\,\mathrm{AM}\,\)の長さを求めれば良いだけです。
中心角はこの長さに比例するので、
　半径\(\,\mathrm{OA}\,\)の周が\(\,24\pi\,\)であることから
　弧\(\,8\pi\,\)に対する中心角は\(\,120°\,\)だと分かります。

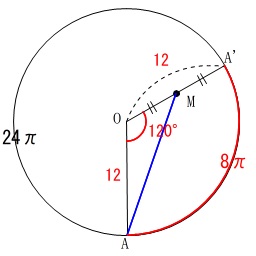
　\(\displaystyle 360^{\circ}\times \frac{8\pi}{24\pi}=120^{\circ}\)

この比例計算は特別な計算方法です。

⇒　比例式の応用 文章題への利用と便利な比の使い方

覚えておくと良いです。

さてこの\(\,\mathrm{\color{blue}{AM}}\,\)はいろいろな求め方ができます。
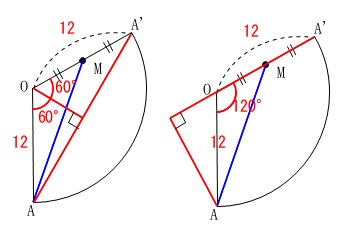普通の中学生向きに右の三平方の定理を利用する方を使いましょう。
\(\,120°\,\)というのが三角定規の1つなので計算を楽にしてくれています。
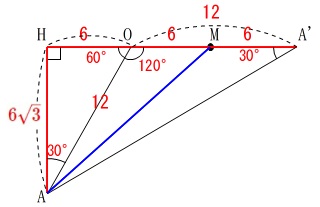三角形\(\,\mathrm{OAH}\,\)は\(\,1:2:\sqrt{3}\,\)の三角定規なので
　\(\,\mathrm{OH=6\,,\,AH=6\sqrt{3}}\,\)
これと
　\(\,\mathrm{HM=HO+OM=12}\,\)
から
\(\,\mathrm{△AMH}\,\)に三平方の定理を利用すると

　\(\begin{eqnarray}
\mathrm{AM^2}&=&\mathrm{AH^2+MH^2}\\
&=&(6\sqrt{3})^2+(12)^2\\
&=&108+144\\
&=&252
\end{eqnarray}\)

\(\mathrm{AM}＞0\)　だから

　\(\begin{eqnarray}
\mathrm{AM}&=&\sqrt{252}\\
&=&\underline{6\sqrt{7}}
\end{eqnarray}\)

ちょっと余裕のある中学生ならパップス使って良いですよ。

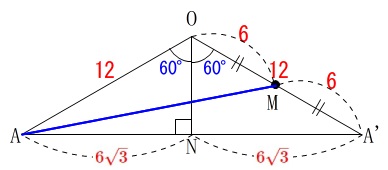
　\(\begin{eqnarray}
\mathrm{AO^2+AA’^2}&=&2(\mathrm{OM^2+\color{blue}{AM}^2})^2\\
12^2+(12\sqrt{3})^2&=&2(6^2+\mathrm{\color{blue}{AM}^2})\\
144+144\times 3&=&2(36+\mathrm{\color{blue}{AM}^2})\\
144+432&=&72+2\mathrm{\color{blue}{AM}^2}\\
576-72&=&2\mathrm{\color{blue}{AM}^2}\\
504&=&2\mathrm{\color{blue}{AM}^2}\\
\mathrm{\color{blue}{AM}^2}&=&\frac{504}{2}\\
&=&252
\end{eqnarray}\)

　∴　\(\,\mathrm{\color{blue}{AM}=\underline{6\sqrt{7}}}\,\)

\(\,\mathrm{AM}\,\)は中線なので使ってみましたが、
試験会場で手を動かしたとすれば最初の解説で示した垂線でしょう。

問3は一般試験の問3と同じです。

⇒　埼玉県公立高校入試の過去問から規則性の問題を攻略する方法

問4は一般入試の問4と少し日本語が違いますが答えは同じです。

⇒　埼玉県公立入試2018の過去問で差がつく関数問題の解き方がわかる

角の二等分線定理の証明

問5(1)は角（内角）の二等分線定理の証明です。
残念ですが中学の教科書にはありません。
なのに、中学校の先生によりますが、定期テストでは定理を知ってるかのように出るんですよね。

入試では相似の応用として出題されます。
補助線の引き方を知らない一般の高校生は二等分線定理は使えても証明ができない人も多いです。
（証明よりは使えることが優先で良いですけど。）

補助線は垂線か平行線ですよ。
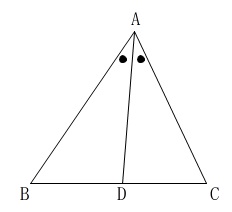\(\,\mathrm{AB:AC=BD:DC}\,\)を証明します。
平行線を引いて相似の性質を利用しますが、平行線の引き方は二通り予想できます。

　・\(\,\mathrm{D}\,\)から\(\,\mathrm{CA\,,\,BA}\,\)に平行な線を引く。
　・\(\,\mathrm{C}\,\)から\(\,\mathrm{DA}\,\)に平行な線を引く。

どっちでも二等辺三角形を見つけて等しい辺を置きかえる、というのは同じです。

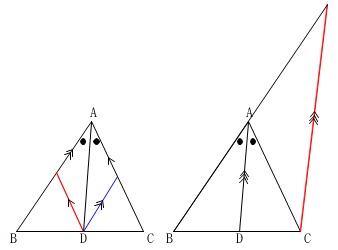
ひし形ができるので左の平行線の方が証明しやすいのか、と思いますが右の方が分かり易いです。笑
一般的に右の平行線を引く方が証明に使われます。

証明しておきます。
（証明）
直線\(\,\mathrm{BA}\,\)と\(\,\mathrm{C}\,\)から\(\,\mathrm{BA}\,\)に平行な直線との交点を\(\,\mathrm{E}\,\)とすると、
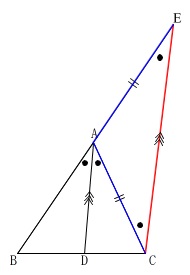平行線の同位角および錯角と仮定から
　\(\mathrm{∠AEC=∠BAD=∠BAC=∠ACE}\)
なので\(\,\mathrm{△ACE}\,\)は二等辺三角形で、
　\(\mathrm{\color{blue}{AC}=\color{blue}{AE}}　･･･①\)
また、\(\,\mathrm{AD /\!/ EC}\,\)だから
　\(\mathrm{BA:\color{blue}{AE}=BD:DC}\)
①から
　\(\mathrm{AB:\color{blue}{AC}=AB:\color{blue}{AE}=BD:DC}\)
（終わり）

この証明では、
　平行線を引いて\(\,\mathrm{△ACE}\,\)が二等辺三角形
であることをしめしましたが、
\(\,\mathrm{BA}\,\)の延長上に\(\,\mathrm{AC=AE}\,\)となる点\(\,\mathrm{E}\,\)をとり、

　\(\,\mathrm{△ACE}\,\)が二等辺三角形であることと仮定から
　\(\,\mathrm{AD}\,\)と\(\,\mathrm{EC}\,\)が平行

を示しても同じ証明になります。

ひし形を利用する証明は必要ないでしょう。
ややこしくなるだけです。笑

円に内接する四角形の辺の長さと相似

\(\,\large{5}\,\)(2)は①と②があります。
①に入る前に条件が与えられているので②についてもいえる条件です。

条件
　\(\,\mathrm{∠BAP=∠CAP}\,\)
　\(\,\mathrm{AB=5}\,\)
　\(\,\mathrm{AC=4}\,\)
　\(\,\mathrm{CP=\sqrt{5}}\,\)
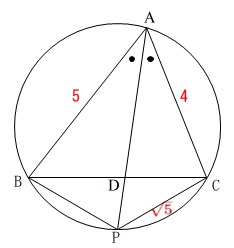円に内接しているので円周角などの条件が加わります。
①円に内接する四角形の1辺を求める問題です。

答えは出ています。
\(\,\mathrm{△PBC}\,\)は底角が等しいことから二等辺三角形なので
　\(\,\mathrm{BP=\underline{\sqrt{5}}}\,\)

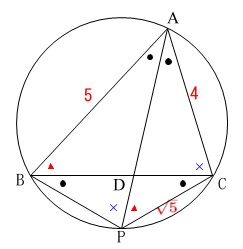
②線分\(\,\mathrm{AD}\,\)の長さを求めますが、(1)が誘導になっています。
何のために(1)があるかですね。

定理を導くだけなら小問集合で良いのですが、総合問題で入れているということは次で使うということです。
使わない場合もありますが、裁量問題や学校選択問題がある難しめの問題ほど誘導になっています。

(1)なしで(2)があるとすればもう一段階難易度は上がりますね。
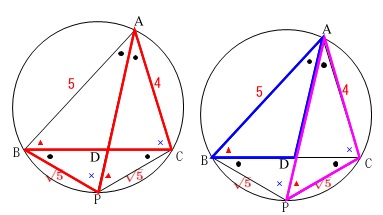2つの相似を使いますが相似な三角形はいろいろあるので適当に見つけると良いです。
これでないといけないということはありません。
ただし、どの相似でも長さが求まるとは限りませんので、試してみることは必要になります。
ここでは上に示した2つの相似を使って答えを出しておきます。

途中の説明も書くように指示があるので、解説を部分的に切り取って書いておけば大丈夫です。

　\(\,\mathrm{△\color{red}{B}D\color{blue}{P}}\,\)　∽　\(\,\mathrm{△\color{red}{A}D\color{blue}{C}}\,\)
なので
　\(\,\mathrm{\color{red}{B}D:\color{red}{A}D=D\color{blue}{P}:D\color{blue}{C}=\color{blue}{P}\color{red}{B}:\color{blue}{C}\color{red}{A}}\,\)
(1)で証明したことから
　\(\,\mathrm{BD:DC=AB:AC=5:4}\,\)
だから
　\(\,\mathrm{BD}=5x\,,\,\mathrm{DC}=4x\,\)
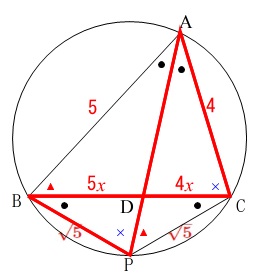とおくと　
相似比が出ているので\(\,\mathrm{DP\,,\,AD}\,\)を\(\,x\,\)で表すことができます。

　\(\,\sqrt{5}:4=5x:\mathrm{AD}\,\)
なので
　\(\begin{eqnarray}
\sqrt{5}\times \mathrm{AD}&=&20x\\
\mathrm{AD}&=&\frac{20}{\sqrt{5}}x\\
&=&4\sqrt{5}x
\end{eqnarray}\)

また
　\(\,\sqrt{5}:4=\mathrm{DP}:4x\,\)
なので
　\(\begin{eqnarray}
4\times \mathrm{DP}&=&4\sqrt{5}x\\
\mathrm{DP}&=&\sqrt{5}x\\
\end{eqnarray}\)

これらを図に書き込むと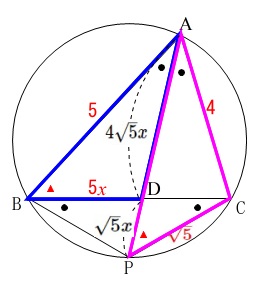次に二つ目の相似にニコちゃんマークを使います。
　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△APC}\,\)
において
　\(\,\mathrm{AB:AP=BD:PC=DA:CA}\,\)
また
　\(\,\mathrm{AP=AD+DP=5\sqrt{5}}\,x\)
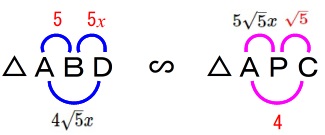なので
　
　\(\begin{eqnarray}
5:5\sqrt{5}x&=&5x:\sqrt{5}\\
25\sqrt{5}x^2&=&5\sqrt{5}\\
\displaystyle x^2&=&\frac{1}{5}\\
x&=&\frac{1}{\sqrt{5}}　(x＞0)
\end{eqnarray}\)

よって
　\(\begin{eqnarray}
\mathrm{AD}&=&4\sqrt{5}x\\
\displaystyle &=&4\sqrt{5}\times \frac{1}{\sqrt{5}}\\
&=&\underline{4}
\end{eqnarray}\)

文字の置き方は自分のやりやすいようにおいて良いです。
相似の取り方も(1)の二等分線定理の証明で使った相似でも良いです。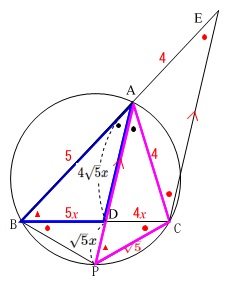チャレンジしてみてください。
文字設定は同じにして
　\(\,\mathrm{△PBC}\,\)　∽　\(\,\mathrm{△AEC}\,\)
を先に利用すると、
　\(\,\displaystyle \mathrm{AD=\frac{5}{9}CE=4\sqrt{5}}x\,\)
が出てきます。

もちろん他にも方法はあります。

トレミーの定理なんかは使いたくなる設定ですよね。

⇒　中学生ができるトレミーの定理の証明方法

『覚え太郎』会員は使って良いですよ。
文字設定して、『トレミーの定理より』、とまとめておけば論理的には間違いではないので減点はありません。
高校の先生は当然知っているので問題ないですよ。

でも、
余裕ありすぎて学校の先生にチャレンジする、
冒険好きな通塾生じゃないので入試では普通に解くことをおすすめしておきます。笑

これで埼玉県2018年度の公立高校入試の学校選択問題は終わりです。

　（以上で問題は終わりです。）

と問題用紙に書いてくれているのは非常にありがたいですね。

解答用紙を見れば解答欄がないので気がつきますが、
問題が自分だけ抜け落ちていたらどうしよう、という心配がありません。笑

⇒　埼玉県公立高校入試の数学（一般・学校選択）過去問と解説

（解説の更新が確認できます。）

全国には似たレベルの公立入試もあります。
ですが先ずは埼玉県立高校入試の傾向の変化を見ておくと良いです。