秋田県で2018年(平成30年度)に行われた公立高校入試の数学の過去問と解説です。
ここでは一般選抜試験の問1の解説になります。
中学で習った数学の基本用語をしっかり理解していれば難しい問題はありませんが、
注意点がいくつかありましたのでお伝えしておきます。
秋田県の入試問題の注意点
秋田県の受験生は知っているだろうけど、秋田県の数学は\(\,\large{1}\,\)だけで\(15問\)あります。
しかし、これ全部解かなくて良いのです。
なんか公立入試にしては分量多いな、と思いながらていねいに別解まで考えながら\(問5\)まで全部解き終えて時計見たら\(30\)分近くかかっていて、
こりゃ受験生もたいへんだなとよく見たら\(\,\large{1}\,\)と\(\,\large{5}\,\)は選択問題がありました。
\(\,\large{1}\,\)は\(15\)問のうち\(8\)問を選択して解きます。
ですが、学校ごとに指定されるので勝手に\(8\)問を選ぶことはできません。
受験する高校の指定問題を間違えないようにしましょう。
最初に「指示された\(8\)問について答えなさい。」というのは目についたのですが何のこと？
と思いながらスルーしてしまったのがいけませんでした。
問題はよく読み、注意書きにもしっかり目を通しておきましょう。笑
解説です。
\(\Large{1}\)
多いのでちゃっちゃとかたづけていきましょう。
正の数負の数と文字式と無理数の計算
(1)2つ計算がありますが、足し算引き算かけ算割り算の順序を間違えなければ良いだけです。
かけ算割り算が先ですよ。
①
\(\hspace{10pt}4-5\times 3\\
=4-15\\
=\underline{-11}\)
（かっこ）がある場合は中の計算が先です。
②
\(\hspace{10pt}(4-5)\times 3\\
=(-1)\times 3\\
=\underline{-3}\)
(2)割り算は逆数のかけ算で、会員サイトにある『約分の効用』を利用するだけです。
\(\displaystyle\hspace{10pt} \frac{4}{3}ab^2\color{red}{\div 2b} \times (-3a)\\
\displaystyle =\frac{4ab^2}{3}\color{red}{\times \frac{1}{2b}}\times (-3a)\\
\displaystyle =-\frac{4ab^2\times 3a}{3\times 2b}\\
=-2a^2b\)
会員はいつものように分数線は1つで進めてくださいね。
(3)素因数分解してルートの中を簡単にして、有理化するだけです。
素因数分解すると
\(3\underline{)\hspace{4pt}27}\\
3\underline{)\hspace{8pt}9}\\
\hspace{16pt}3\)
よって \(\color{blue}{27=3^2\times 3}\)
※
素因数分解というのは数学の用語です。覚えておきましょう。
素数で分解していくのです。
\(\hspace{10pt}\displaystyle \color{blue}{\sqrt{27}}-\frac{6}{\sqrt{3}}\\
\displaystyle =\color{blue}{3\sqrt{3}}-\frac{6\color{red}{\times \sqrt{3}}}{\sqrt{3}\color{red}{\times \sqrt{3}}}\\
\displaystyle =3\sqrt{3}-\frac{6\sqrt{3}}{3}\\
=3\sqrt{3}-2\sqrt{3}\\
=\underline{\sqrt{3}}\)
１次方程式と代入のポイントと２次方程式
(4)方程式の解とは、方程式を満たすものです。
つまり、代入して成り立たなければ解とは言いません。
解が\(\,3\,\)なので\(\,x=3\,\)を方程式に代入しましょう。
するとどうなるか、とか余計なことは考えなくて良いのです。
方程式の解なら代入して成り立つことを利用するようになっているはずです。
\(\begin{eqnarray}
2x+a-1&=&0\\
2(3)+a-1&=&0\\
6+a-1&=&0\\
5+a&=&0\\
a&=&\underline{-5}
\end{eqnarray}\)
どストレートに答えでした。ｗ
代入するときは正の数でも負の数でも（かっこ）をつけて代入すると計算ミスは減ります。
(5)この問題のように、\(\,x,y\,\)の値が与えられて、関係式の値を求めるとき、
\(\displaystyle x=\frac{1}{5}\,,\,y=3\)
のような式の値を「条件式」、
\(3(x-5y)-2(4x-7y)\)
のような値を求める式を「与式」、または「求値式」と言います。
この用語は高校になって使えば良いですが、
求値式を簡単にして条件式を代入
という順序で計算しましょう。
最初から代入するとたいへんな計算になることが多いですので、
いつも条件式をできるだけ処理してから代入するようにしておくと高校に行ってからも数学らしく計算できます。
\(\hspace{10pt}3(x-5y)-2(4x-7y)\\
=3x-15y-8x+14y\\
=-5x-y\\
\displaystyle =-5\times \left(\frac{1}{5}\right)-(3)\\
=-1-3\\
=\underline{-4}\)
これ、たまたま分母が消えたのではありません。
与式変形からすれば計算が楽になるように問題を作ってくれているのです。
偉そうに聞こえるかもしれないだけど、
秋田県の問題は全体を通じて数学の力を試せるようによく考えられていますよ。
解いてみて、数学らしくやらないと通じないところもあって、
しっかり作業しなければ答えが出ない問題もあり、
『超え太郎』マスター向けに答えに直結する方法を密かに忍ばせてある問題もありました。
(6)方程式を解くことと、方程式の解を求めることは同じことです。
2次方程式の場合、解の公式があるので計算に自信があればすべて解の公式で解けば良いですが時間がかかってしまいます。
文章問題ではほとんどが因数分解できる2次方程式になるので因数分解から試しておくと良いです。
この問題のように小問集合のときは解の公式を利用する問題が多いですが、ここでは因数分解です。
\(x^2\color{blue}{-5}x\color{red}{+6}=0\)
定数の \(\,\color{red}{+6}\,\) に着目です。
かけて\(\,6\,\)になるのは
\(\color{black}{\fbox{ 1×6 }}\) \(\color{red}{\fbox{ 2×3 }}\)
だけですが、かけて＋になるのは「両方（＋）」か「両方（－）」で、
足して\(\,x\,\)の\(\,\color{red}{\color{blue}{1\,次の係数-5}}\)になるのは\(\,-2\,\)と\(\,-3\,\)の組。
\(\begin{eqnarray}
x^2-5x+6&=&0\\
(x-2)(x-3)&=&0\\
x&=&\underline{2\,,\,3}
\end{eqnarray}\)
反比例と速さの関係式と中央値の意味
(7)問題に「\(\,y\,\)が\(\,x\,\)に反比例する」という言葉を見たら、
\(\,\displaystyle y=\frac{a}{x}\,\)
となるので比例定数を求めに行くのは当たり前のことですよね。
表の\(\,x=3\,\)のとき\(\,y=2\,\)を代入すると
\(\displaystyle 2=\frac{a}{3}\,\)これから \(\,a=6\,\)
なので
\(\,\displaystyle y=\frac{6}{x}\,\)
と関数が決まります。
\(\,x=-1\,\)を代入すれば答えです。
\(\,\displaystyle y=\frac{6}{-1}=\underline{-6}\,\)
比例 \(\,y=\color{red}{a}x\,\)
反比例 \(\displaystyle y=\frac{\color{red}{a}}{x}\)
\(\,y\,\)が\(\,x^2\,\)に比例する関数 \(\,y=\color{red}{a}x^2\,\)
これらの\(\,\color{red}{a}\,\)すべてを比例定数といいますので覚えておきましょう。
(8)道のりと速さと時間の関係なので小学生でもできます。
文字が入ると時間がかかって、わからなくなるのは図を書かないからです。
簡単な線分図で良いので書けば良いのに書かない人が多いです。
「サイクリングコース」問題に関係ありません。
「自転車」問題に関係ありません。
\(\,\displaystyle \color{red}{時間＝\frac{道のり}{速さ}}\,\)
なので
\(\,a\,\mathrm{km}\,\)を時速\(\,13\mathrm{km}\,\)で移動した時間は
\(\,\displaystyle \color{red}{\frac{a}{13}}\,\)
\(\,b\,\mathrm{km}\,\)を時速\(\,18\mathrm{km}\,\)で移動した時間は
\(\,\displaystyle \color{blue}{\frac{b}{18}}\,\)
合わせて\(\,1時間\,\)
これが問題に必要な数値です。
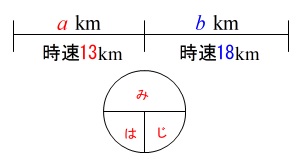
\(\,\displaystyle \underline{\frac{a}{13}+\frac{b}{18}=1}\,\)
等式になっているのでこれ以上変形する必要はありません。
\(\,\color{red}{時間}＋\color{blue}{時間}＝時間\,\)
で意味の通る立派な等式です。
(9)度数分布表ですが階級に幅がありません。
階級の数値そのものが階級値です。
資料の整理の基本は小さい順にデータを並べることです。
それを書き出すか書き出さないかで大きく変わります。
※
度数が大きくて書き出せない場合も多いですが、おおよそのデータを並べてみるとわかります。
中央値は値の小さい順に並べたときに順番で真ん中に来る値です。
例えば
\(\,1,2,2,\color{red}{5},6,6,7\,\)
と\(\,7\,\)つのデータが並んだとすると真ん中は\(\,4\,\)番目になるので
中央値は\(\,\color{red}{5}\,\)です。
ただし、データの数が偶数のときは、
\(\,1,2,2,\color{blue}{4},\color{blue}{6},6,7,8\,\)
左\(\,4\,\)つ右\(\,4\,\)つで真ん中のデータがありません。
このようなときは\(\,\color{red}{真ん中2つの平均}\,\)を中央値とします。
\(\,\displaystyle \frac{\color{blue}{4+6}}{2}=\color{red}{5}\,\)
この問題は度数が\(\,17\,\)だから真ん中は\(\,9\,\)番目になります。
\(○○○○○○○○－\color{red}{○}－○○○○○○○○\)
つまり、得点の低い順番に並べたときの\(\,\color{red}{9人目}\,\)の人の得点が中央値です。
問題は
「\(\,\color{red}{中央値が2点}\,\)」
の場合なので\(\,\color{red}{9番目に2}\,\)が入る場合を考えます。
小さい方の階級\(\,0と1で7\,人\)います。
大きい方からみると階級\(\,4と5で6人\,\)います。
\(\,\color{red}{残りは4人}\,\)です。
\(0,0,0,1,1,1,1,○,\color{red}{●},○,○,4,4,4,4,5,5\)
階級\(\,2と3で4人\,\)入るとき
\(\,\color{red}{●}に2\,\)が入るのは何通りあるか？
という問題に変わりました。
左の方には小さい数字\(\,2\,\)しか入らないことを考えて
\(2,\color{red}{2},2,2\)
\(2,\color{red}{2},2,3\)
\(2,\color{red}{2},3,3\)
というデータの並びしか考えられません。
\(2,\color{red}{3},3,3\)
となれば\(\,\color{blue}{中央値が3}\,\)となり、問題に合わなくなります。
（答え）\(\,\underline{3\,組}\,\)
データ、並べてみましたか？
無理数を自然数にする最大の数
(9)無理数全体が自然数になる\(\,n\,\)の最大値を求めます。
これはよく見る問題なので説明はいらないかもしれませんが、簡単に説明しておきます。
\(\sqrt{\mathrm{A}}\) が自然数になるということは
ルートが外れるということなので\(\,k\,\)を自然数として
\(\mathrm{A}\) が \(\,\mathrm{A}=k^2\,\)の形の平方数であるということです。
\(\,\sqrt{\mathrm{A}}=\sqrt{k^2}=k\,\)
（\(\,k\,\)は自然数なので\(\,\pm\,\)は考えなくて良いです。）
例えばルートの中が平方数なら
\(\,\sqrt{2^2}=2\,\)
\(\,\sqrt{5^2}=5\,\)
ですが
\(\,\sqrt{8}=2\sqrt{2}\,\)
\(\,\sqrt{12}=2\sqrt{3}\,\)
のように平方数でない場合はルートはなくなりません。
問題は
\(\,\sqrt{306-3n}\,\)が自然数となる\(\,\color{red}{最大}\,\)の整数\(\,n\,\)
を求めることです。
整数なので順番に調べていけば良いだけです。
まさか小さい\(\,n=1\,\)から調べる人はいないでしょう。
いても大きい方から調べた方がはやい気がつくと思います。笑
自然数、整数が混じっていてややこしく見えますが、
\(\,n\,\)は整数だけど\(\,306-3n\,\)は\(\color{red}{\,0\,ではない}\,\)
といっているだけです。
たぶん、人によって2つの方法に分かれるでしょう。
\(\,306-3n=0\,\)のとき\(\,n=102\,\)なので
\(n≦101\) を考え\(\,n=101\,,\,100\,,\,\cdots\,\)を調べていく方法
\(\,n=101\,\)のとき
\(\hspace{10pt}\sqrt{306-3\times 101}\\
=\sqrt{306-303}\\
=\sqrt{3}\, (×)\)
\(\,n=100\,\)のとき
\(\hspace{10pt}\sqrt{306-3\times 100}\\
=\sqrt{306-300}\\
=\sqrt{6}\, (×)\)
\(\,n=99\,\)のとき
\(\hspace{10pt}\sqrt{306-3\times 99}\\
=\sqrt{306-297}\\
=\sqrt{9}=3\, (○)\)
（答え）\(\,n=\underline{99}\,\)
逆に、
\(\,n\,\)が\(\,\color{blue}{最も大きいとき}\,\)
\(\,\sqrt{306-3n}\,\)は最も小さい自然数になる
ということなので
\(\sqrt{306-3n}=1\)
\(\sqrt{306-3n}=2\)
\(\sqrt{306-3n}=3\)
\(\,\cdots\,\)
と順番に調べる方法があります。
\(\,\sqrt{306-3n}=1\,\)のとき
\(\begin{eqnarray}
306-3n&=&1^2\\
306-3n&=&1\\
-3n&=&1-306\\
-3n&=&-305\\
\displaystyle n&=&\frac{305}{3}
\end{eqnarray}\)
\(\,\sqrt{306-3n}=2\,\)のとき
\(\begin{eqnarray}
306-3n&=&2^2\\
306-3n&=&4\\
-3n&=&4-306\\
-3n&=&-302\\
\displaystyle n&=&\frac{302}{3}
\end{eqnarray}\)
\(\,\sqrt{306-3n}=3\,\)のとき
\(\begin{eqnarray}
306-3n&=&3^2\\
306-3n&=&9\\
-3n&=&9-306\\
-3n&=&-297\\
\displaystyle n&=&\frac{297}{3}\\
&=&\underline{99}
\end{eqnarray}\)
でも同じことです。
中には\(\,k\,\)を自然数とすると
\(\,360-3n=k^2\,\)
とおけるので、
\(\,3n=360-k^2\,\)
で\(\,k=1\,,\,2\,,\,3\,,\,\cdots\,\)と入れていって
\(\,360-k^2\,\)が\(\,\color{red}{3\,で割り切れるか}\,\)
を調べる人もいるでしょう。
良いですよ。
\(\begin{eqnarray}
3n&=&360-k^2\\
\displaystyle n&=&\frac{360-k^2}{3}
\end{eqnarray}\)
\(\,n\,\)は整数なので右辺の分子は\(\,\color{blue}{3\,の倍数}\,\)です。
さらにいえば
\(\begin{eqnarray}
\displaystyle n&=&\frac{360-k^2}{3}\\
&=&120-\frac{k^2}{3}
\end{eqnarray}\)
なので
\(\,\color{red}{k\,自身が\,3\,の倍数でなければならない}\,\)
こともわかります。
論理的にいえばこれを示さなければなりませんが、ここでは必要ないでしょう。
ここまで答えを出した方法はやっていることは同じなのですが、
地道な作業をしようとしているか、していないかの違いです。
まだ(9)です。(15)まであるんですよ。
2,3分で解ける問題をどれだけ時間かけてんだって話です。笑
円に内接する四角形が作る円周角と平行線できる角の求め方
(11)直径に対する円周角は90度です。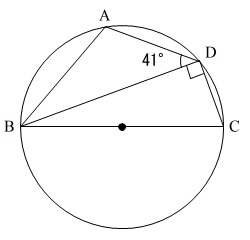
円に内接する四角形において、
\(\,\color{red}{対角の和が\,180\,度}\,\)
ということを知っていれば
\(\begin{eqnarray}
\mathrm{∠ABC+\color{red}{∠ADC}}&=&180^{\circ}\\
\mathrm{∠ABC}&=&180^{\circ}-\mathrm{\color{red}{∠ADC}}
\end{eqnarray}\)
なので
\(\begin{eqnarray}
\mathrm{∠ABC}&=&180^{\circ}-(\color{red}{41^{\circ}+90^{\circ}})\\
&=&180^{\circ}-\color{red}{131^{\circ}}\\
&=&\underline{49^{\circ}}
\end{eqnarray}\)
とすぐに出るので『覚え太郎』会員はこっちで良いです。
ほとんどの中学校では教えてもらっていると思うのですが、
教科書にないのでくどくなるけど説明しておきます。
円周角とセットで考えるのは中心角です。
\(\,\mathrm{∠ADC}の中心角は\mathrm{∠AOC}\,\)
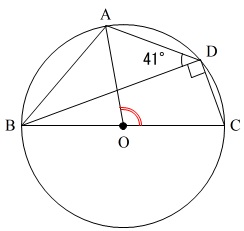ではありません。
\(\,\mathrm{∠AOC}\,\)の\(\,\mathrm{B}\,\)側の中心角です。
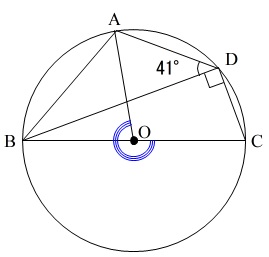
中心角は円周角の2倍なので
\(\begin{eqnarray}
\mathrm{∠AOC}&=&2\times (41^{\circ}+90^{\circ})\\
&=&2\times 131^{\circ}\\
&=&262^{\circ}
\end{eqnarray}\)
この角度の反対側が\(\,\mathrm{∠ABC}\,\)の中心角になります。
弧\(\,\mathrm{ABC}\,\)の中心角は
\(\,\mathrm{∠AOC}=360^{\circ}-262^{\circ}=98^{\circ}\,\)
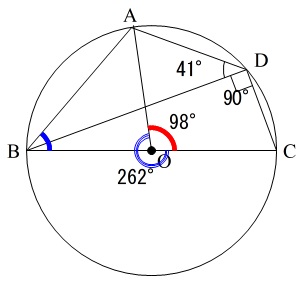この円周角が答えです。
\(\,\displaystyle \mathrm{∠ABC}=\frac{98^{\circ}}{2}=\underline{49^{\circ}}\,\)
中心と\(\,\mathrm{D}\,\)を結ぶと二等辺三角形がたくさんできるので、
二等辺三角形の底角が等しいことを利用しても答えは出ます。
(12)
角度を求めるときは図の中でわかる角度を次々に書き出せばほとんど答えも求まっています。
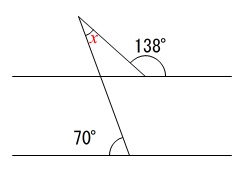平行線で等しいのは同位角と錯角です。
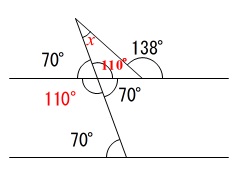
もう一つの内角も
\(\,180^{\circ}-138^{\circ}=42^{\circ}\,\)
と出るので三角形の内角の和が\(\,180°\,\)であることから
\(\begin{eqnarray}
x+110^{\circ}+42^{\circ}&=&180^{\circ}\\
x+152^{\circ}&=&180^{\circ}\\
x&=&\underline{28^{\circ}}
\end{eqnarray}\)
でも良いのですが
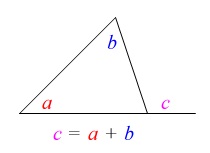を使うとはやいです。
\(\begin{eqnarray}
x+110^{\circ}&=&138^{\circ}\\
x&=&138^{\circ}-110^{\circ}\\
&=&\underline{28^{\circ}}
\end{eqnarray}\)
台形の中の線分の求め方と回転体の体積と円すいの高さ
(13)
台形の線分の長さ問題です。
図形問題では図に条件を書き込むことから始めます。
条件は
\(\,\mathrm{ＡＤ}\,\) ∥ \(\,\mathrm{ＢＣ}\,\)
\(\,\mathrm{Ｅ}\,,\,\mathrm{Ｆ}は\mathrm{ＡＢ\,,\,ＣＤ}の中点\,\)
\(\,\mathrm{AD=3}\,\)
\(\,\mathrm{BC=11}\,\)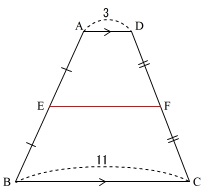
これは『覚え太郎』会員は見た瞬間に答えが出ますね。
\(\begin{eqnarray}
\displaystyle \mathrm{EF}&=&\frac{3+11}{2}\\
&=&\frac{14}{2}\\
&=&\underline{7}
\end{eqnarray}\)
普通に平行線の性質を利用して解いてみましょう。
\(\,\mathrm{DC}\,\)に平行になるように\(\,\mathrm{AG}\,\)を引きます。
\(\,\mathrm{AE=EB\,,\,DF=FC}\,\)
なので
\(\,\mathrm{AD}\,\) ∥ \(\,\mathrm{EF}\,\) ∥ \(\,\mathrm{BC}\,\)
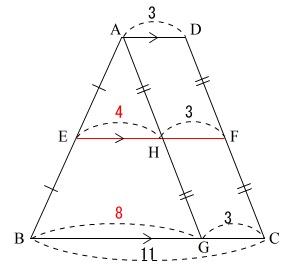\(\,\mathrm{AG}\,\)と\(\,\mathrm{EF}\,\)の交点を\(\,\mathrm{H}\,\)とすると
\(\,\mathrm{ADCG}\,\)と\(\,\mathrm{ADFH}\,\)は平行四辺形なので
\(\mathrm{AD=\color{blue}{HF}=\color{red}{GC}=\color{red}{3}}\)
となり
\(\begin{eqnarray}
\mathrm{BG}&=&\mathrm{BC-\color{red}{GC}}\\
&=&11-\color{red}{3}\\
&=&8
\end{eqnarray}\)
さらに、中点連結定理より
\(\begin{eqnarray}
\displaystyle \mathrm{\color{magenta}{EH}}&=&\frac{1}{2}\times\mathrm{BG}\\
&=&\frac{1}{2}\times 8\\
&=&\color{magenta}{4}
\end{eqnarray}\)
よって
\(\begin{eqnarray}
\mathrm{EF}&=&\mathrm{\color{magenta}{EH}+\color{blue}{HF}}\\
&=&4+3\\
&=&\underline{7}
\end{eqnarray}\)
平行線は\(\,\mathrm{AB}\,\)に引いても同じです。
補助線を引くときは、平行か垂直、と思っていて良いです。
※
トレミーの定理の証明で平行線や垂線でない線を引きましたが、あれは例外です。
(14)
回転体の体積を求める場合はだいたいの見取り図を書いて考える方が良いですよ。
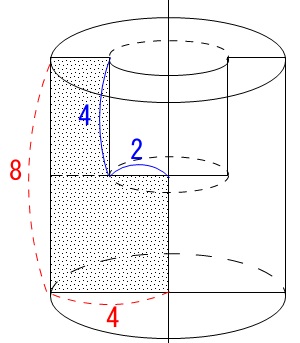回転体の体積ですが円柱から円柱をくり抜けば終わります。
大きい円柱は
\(\,\color{red}{底面の半径\,4}\,\) \(\,\color{red}{高さ\,8}\,\)
なので体積は
\(\hspace{10pt}\pi (4)^2\times 8\\
=\color{red}{128\pi}\)
小さい円柱は
\(\,\color{blue}{底面の半径\,2}\,\) \(\,\color{blue}{高さ\,4}\,\)
なので体積は
\(\hspace{10pt}\pi (2)^2\times 4\\
=\color{blue}{16\pi}\)
よって求める回転体の体積は
\(\color{red}{128\pi}-\color{blue}{16\pi}=\underline{112\pi}\)
公式のない体積問題は「部分＋部分」か「全体－部分」で求めると良いですね。
回転体の公式はあるにはありますがここでは紹介しません。
『超え太郎』マスターは使って良いですよ。
(15)
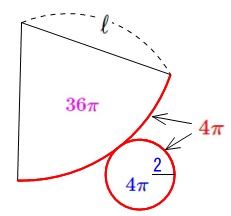
円錐の高さを求める問題です。
円錐（すい）が漢字になっていることから簡単な問題ではないのかな？
と思ったら普通の手順ですぐに答えが出ました。笑
思い込みはいけません！
高さを求めるには円錐の母線が必要になりますので、母線の長さを求めることを最初の目的にします。
母線の長さを求めるのに必要な条件は問題に与えられています。
条件を書き出すと
\(\,底面の半径が\,2\,\)
\(\,表面積が\,40\pi\,\)
これだけです。
『表面積』とあるので展開図ですね。
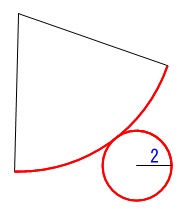底面の円周と扇形の弧の長さが等しい、は良いですね。
基本中の基本です。
半径\(\,2\,\)の円周は\(\,\color{red}{4\pi}\,\)
これは弧の長さでもあります。
底面の面積は \(\,\pi \times (2)^2=\color{blue}{4\pi}\,\)
なので、扇形の面積は表面積全体から底面の面積を引いた
\(\,40\pi -\color{blue}{4\pi}=\color{magenta}{36\pi}\,\)
解法が分かれるのはここからです。
求めたいのは高さの前に、母線の長さなので母線の長さを\(\,\ell\,\)とします。
母線の長さ（扇形の半径）\(\,\ell\,\)、
弧の長さ\(\,4\pi\,\)のとき
扇形の面積が
\(\,\displaystyle \frac{1}{2}\times 4\pi \times \ell\,\)
になることを知っていれば
\(\,\displaystyle \frac{1}{2}\times 4\pi \times \ell=\color{magenta}{36\pi}\,\)
から
\(\ell=18 \)
とすぐに求まりますが、一般的ではありません。
扇形の弧と面積は中心角に比例する関係を利用します。
扇形の中心角を\(\,a\,\)としましょう。
扇形の半径は\(\,\ell\,\)なので
弧の長さは
\(\,\displaystyle 2\pi \ell\times \frac{a}{360}=\color{red}{4\pi}\,\)
扇形の面積は
\(\displaystyle \pi (\ell)^2\times \frac{a}{360}=\color{magenta}{36\pi}\)
の関係を満たします。
弧の長さの関係式の両辺を2で割ると
\(\,\displaystyle \color{red}{\pi \ell\times \frac{a}{360}}=2\pi\,\)
扇形の面積の関係式の左辺を
\(\hspace{10pt}\displaystyle \pi (\ell)^2\times \frac{a}{360}\\
\displaystyle =\ell \times \color{red}{\pi \ell\times \frac{a}{360}}\)
と変形して代入すると
\(\,扇形の面積=\ell\times 2\pi\,\)
とおけてこの面積が\(\,\color{magenta}{36\pi}\,\)なので
\(\begin{eqnarray}
\ell\times 2\pi&=&36\pi\\
\ell&=&18
\end{eqnarray}\)
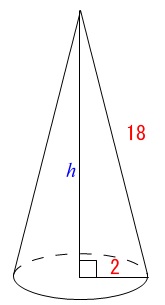
ここで元の円錐に戻ります。
底面の半径が\(\,2\,\)
母線の長さが\(\,18\,\)
母線と半径と高さは直角三角形を作るので、
三平方の定理が使えます。
高さを\(\,h\,\)とすると
\(\begin{eqnarray}
h^2+2^2&=&18^2\\
h^2+4&=&324\\
h^2&=&324-4\\
h^2&=&320\\
h&=&\pm 8\sqrt{5}
\end{eqnarray}\)
\(\,h＞0\,\)なので
円錐の高さは \(\,\underline{8\sqrt{5}}\,\)
\(\,h^2=320\,\)の平方根を求めるところですが、
ここまでこれた人は素因数分解はできるものとしています。
説明すると長いですね。
ちゃちゃっと計算すればすぐなのですが、\(\,\large{1}\,\) ということで説明しておきました。
自分でやってみてください。
順を追って、やることをしっかりやれば聞かれていることは基本的なことですよ。
⇒ 2018(H30)年度秋田県公立高校入試数学の過去問第2問の解説
\(\,\large{2}\,\)も少し少ないですけど\(\,\large{1}\,\)と同じように小問集合です
全国的に小問集合は似たような問題ですが、計算レベルが少し違っているので、
秋田県立入試の計算レベルがどの程度必要かを数年分見て確認しておきましょう。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
