2021年（令和3年）度愛知県公立高校入試Ａの数学問題と解説

２０２１年（令和３年）度愛知県公立高校入試Ａグループの数学問題と解説です。
例年同じような解説をしているので
今回は「先ずは答えを出す」ことと「自分でやるべきこと」を重視して解説してみます。
過去問で詳しく復習や対策したい場合は過去の年度の解説を参照してください。

２０２１年（令和３年）度愛知県公立高校入試Ａグループの数学の問題

構成は昨年度と同じで大問は３問です。

⇒　２０２１年（令和３年）度愛知県公立高校入試Ａ日程の数学の問題

大問数だけ見ると少なく思えますが小問に分かれた問題の量と質は十分ありますので
試験時間を考えると対策は基本を幅広く徹底しておく必要がありますね。

２０２１年（令和３年）度愛知県公立高校入試Ａグループの数学の解説

冒頭でも言いましたが、
時間のかかる解説はしません。

愛知県立高校入試は例年偏りなく基本中心に広い範囲を問題にしています。
多少の応用が入りますが良い復習にはなりますので
過去問を参考に総復習しておくと良いでしょう。
（過去問解説は最後にリンクさせておきますので参考にしてください。）

今回は答えを出すことを優先して解くとどうなるか
（いい加減？ある意味実践的です。）
ある程度の解説を加えながら進めて行きます。

実際の計算より行間はうめましたが暗算しているところがあります。
自分で確認するときは確実に計算しておいてください。

それから、
図もできるだけ入れませんので
問題用紙を印刷して図に書き込むなどして
自分で手を動かして見てください。

人の解答見て自分で解いた気になっている人が多いです。

ここは良い機会です。
力をつけるためにも自分で図を書いて
解説の言っていることが理解できるか試して下さい。

第１問

\(\,\large{1}\,\)

(1)
計算順序を間違えないようにして
　\(\hspace{10pt}5-(-6)\div 2\\
=5+3\\
=\underline{　8　}\)

(2)
分母を１つにして分子の計算に集中するけど、
分子には（かっこ）がついていることを忘れずに
　\(\hspace{10pt}\displaystyle \frac{3x-2}{4}-\frac{x-3}{6}\\
\displaystyle =\frac{3(3x-2)-2(x-3)}{12}\\
\displaystyle =\frac{9x-6-2x+6}{12}\\
\displaystyle =\underline{　\frac{7x}{12}　}\)

係数を別にしておいても間違いではない。
　\(\hspace{10pt}\displaystyle \frac{7}{12}\,x\)

問題に指示がなければどっちでも良い。

(3)
迷うくらいなら部分的にでも計算を進めよう。
あまり暗算はしないように
　\(\hspace{10pt}\displaystyle \frac{3}{\sqrt{2}}-\frac{2}{\sqrt{8}}\\
\displaystyle =\frac{3\sqrt{2}}{2}-\frac{2}{2\sqrt{2}}\\
\displaystyle =\frac{3\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\\
\displaystyle =\underline{　\sqrt{2}　}\)
ちょっと暗算している？

(4)
展開した方が早そうなので
　\(\hspace{10pt}(2x+1)^2-(2x-1)(2x+3)\\
=(4x^2+4x+1)-(4x^2+6x-2x-3)\\
=(4x^2+4x+1)-(4x^2+4x-3)\\
=4x^2+4x+1-4x^2-4x+3\\
=\underline{　4　}\)
実際には暗算したけど見直しでは
２行目と（かっこ）を外す１行は加えます。

(5)
真ん中の自然数を文字で置く方が楽だけど、
もっとも小さい数を求めるので
　\(\begin{eqnarray}\displaystyle
n^2+(n+1)^2+(n+2)^2&=&365\\
3n^2+6n+5&=&365\\
3n^2+6n-360&=&0\\
n^2+2n-120&=&0\\
(n+12)(n-10)&=&0\\
\end{eqnarray}\)
自然数だから\(\,n=10\,\)
答え\(\hspace{10pt}\underline{　10　}\)

３つの連続する自然数を
　\(n-1\,,\,n\,,\,n+1\)
とすると平方の和は
　\(\hspace{10pt}(n-1)^2+n^2+(n+1)^2\\
=3n^2+2\)
これが\(\,365\,\)になるとき
　\(\begin{eqnarray}\displaystyle
3n^2+2&=&365\\
n^2&=&121
\end{eqnarray}\)
自然数だから\(\,n=11\,\)で
これは真ん中の数なので
　答え　\(\,\underline{　10　}\,\)

※
必要なところは入れましたが暗算している部分があります。
行間の計算は確実にしましょう。

(6)
すべて選んで？
であればすべて関数にして確認します。

\(\,ア\,\)　\(\,y=x^3\,\)
\(\,イ\,\)　\(\,xy=50\,\)
\(\,ウ\,\)　\(\,y=2\,\pi\,x\,\)
\(\,エ\,\)　\(\displaystyle \,y=5\times \frac{x}{100}=\frac{1}{20}\,x\,\)

比例の関数も一次関数です。

答え　\(\,\underline{　ウ\,,\,エ　}\,\)

\(\,イ\,\)は\(\,\displaystyle y=\frac{50}{x}\,\)の反比例です。

(7)
「少なくとも」なので余事象の確率をひくとして、
元に戻さないから分母が変わることに気をつけて
　\(\hspace{10pt}\displaystyle 1-\frac{3}{5}\times \frac{2}{4}\\
\displaystyle =\underline{　\frac{7}{10}　}\)

余事象は「二人とも当たりくじをひかない。」です。
　\(\,\mathrm{A}\,\)さんが当たりを引かない確率\(\,\displaystyle \frac{3}{5}\,\)
くじは１つ減っているので
　\(\,\mathrm{B}\,\)さんが当たりを引かない確率\(\,\displaystyle \frac{2}{4}\,\)
なので二人とも当たりを引かない確率は
　\(\hspace{4pt}\displaystyle \frac{3}{5}\times \frac{2}{4}\)
となります。

確率計算になれていない人は
基本通り樹形図で良いです。

数字の\(\,\color{red}{1}\,,\,\color{red}{2}\,,\,3\,,\,4\,,\,5\,\)がくじになっていて
\(\,\color{red}{1}\,,\,\color{red}{2}\,\)があたりだとします。
\(\,\mathrm{B}\,\)さんがくじをひくとき
\(\,\mathrm{A}\,\)さんがひいたくじはなくなっています。

縦が\(\,\mathrm{A}\,\)さん、横が\(\,\mathrm{B}\,\)さんがひいたくじです。
（どっちでも同じですが）
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & 3 & 4 & 5 \\ \hline
\color{red}{1} & × & ○ & ○ & ○ & ○\\ \hline
\color{red}{2} & ○ & × & ○ & ○ & ○\\ \hline
3 & ○ & ○ & × & & \\ \hline
4 & ○ & ○ & & × & \\ \hline
5 & ○ & ○ & & & ×\\ \hline
\end{array}\)

どちらかがあたりをひいている確率は
　\(\displaystyle \frac{14}{20}=\underline{　\frac{7}{10}　}\)

(8)
先ずは比例定数を求め
　\(\hspace{4pt}\displaystyle a=\frac{4}{5}\times 15=12\)
関数を決定して
　\(\hspace{4pt}\displaystyle y=\frac{12}{x}\)

\(\,x\,\)座標が\(\,12\,\)の正の約数であれば良いので
　\(\hspace{4pt}1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\)

答え　\(\,\underline{　6　個　}\,\)

(9)
「交点」なので連立します。
　\(\begin{eqnarray}\displaystyle
3x-5&=&-2x+5\\
5x&=&10\\
x&=&2\\
y&=&1
\end{eqnarray}\)

答え　\(\,\underline{　(\,2\,,\,1\,)　}\,\)

(10)
円周角が\(\,30°\,\)だから中心角は\(\,60°\,\)
\(\,\mathrm{△OBC}\,\)は正三角形なので\(\,\mathrm{BC}\,\)は半径に等しい。

答え　\(\,\underline{　6　\mathrm{cm}}\,\)

第２問

\(\,\large{2}\,\)
(1)から(3)までの３問です。

(1)
四角形を２等分する直線を求めますが
平行四辺形ではないので具体的に面積計算します。

分かる限りの座標や直線は求めておきます。
　\(\,\mathrm{A}\,(\,6\,,\,9\,)\,\)
　\(\,\mathrm{B}\,(\,-4\,,\,4\,)\,\)
　\(\,\mathrm{C}\,(\,0\,,\,9\,)\,\)
　直線\(\,\mathrm{OA}:\displaystyle y=\frac{3}{2}\,x\,\)
　直線\(\,\mathrm{BC}:y=x+9\,\)
※
これらの条件は問題の図中に書き込むことを忘れずに！
グラフがあるのですぐに終わります。

　\(\begin{eqnarray}\displaystyle
\mathrm{△OBC}&=&\frac{1}{2}\times 9\times 4\\
&=&\color{red}{18}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{△OAC}&=&\frac{1}{2}\times 9\times 6\\
&=&\color{blue}{27}
\end{eqnarray}\)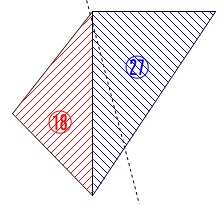だから四角形\(\,\mathrm{CBOA}\,\)の面積は
　\(\hspace{4pt}18+27=45\)
半分は\(\,22.5\,\)なので
線分\(\,\mathrm{OA}\,\)上に\(\,\mathrm{△OPC=4.5}\,\)となる点\(\,\mathrm{P}\,\)を定め
\(\,2\,\)点\(\,\mathrm{C\,,\,P}\,\)を通る直線の式を求めれば良い。

直線\(\,\mathrm{OA}\,\)は\(\displaystyle \,y=\frac{3}{2}\,x\,\)だから
　\(\displaystyle \mathrm{P}\,\left(\,t\,,\,\frac{3}{2}\,t\,\right)\)
とすると\(\,\mathrm{△OCP}\,\)の面積が\(\,4.5\,\)であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△OCP}&=&4.5\\
\frac{1}{2}\times 9\times t&=&\frac{9}{2}\\
t&=&1
\end{eqnarray}\)

\(\,2\,\)点
　\(\,\mathrm{C}\,(\,0\,,\,9\,)\,\)
　\(\,\mathrm{P}\displaystyle \,\left(\,1\,,\,\frac{3}{2}\,\right)\)
を通る直線は
　　\(\hspace{4pt}\displaystyle \underline{\underline{　y=-\frac{15}{2}\,x+9　}}\)

\(\,\mathrm{△CAP=22.5}\,\)としても底辺や高さが軸と平行に取れるので
\(\,2\,\)等分する\(\,\mathrm{OA}\,\)上の点\(\,\mathrm{P}\,\)は簡単に求まりそうです。

やってないけどやってみてください。

(2)
合計が\(\,120\,\)ということは
本数と人数の積の合計が\(\,120\,\)だから
　\(\hspace{4pt}3x+6y+84=120\)
\(\,x\,\)について整理すると
　\(\begin{eqnarray}\displaystyle
3x&=&120-(84-6y)\\
&=&36+6y\\
x&=&\underline{　12-2y　}
\end{eqnarray}\)

\(\,x\,,\,y\,\)ともに自然数だから
　\(\,y=1\,,\,2\,,\,3\,,\,4\,,\,5\,\)
に対して\(\,x\,\)も\(\,5\,\)個自然数となるので
\(\,x\,,\,y\,\)の組は\(\,\underline{　5　}\,\)組ある。

\(\,(\,x\,,\,y\,)\,\)の\(\,5\,\)組は
　\((\,10\,,\,1\,)\)
　\((\,8\,,\,2\,)\)
　\((\,6\,,\,3\,)\)
　\((\,4\,,\,4\,)\)
　\((\,2\,,\,5\,)\)

最頻値が\(\,6\,\)のとき
\(\,y\,\)だけが最大度数となることから
　\(\,x=\underline{　2　}\,,\,y=\underline{　5　}\,\)

\(\,(\,x\,,\,y\,)\,\)が\((\,4\,,\,4\,)\)のときは
最頻値は\(\,3\,\)と\(\,6\,\)になります。
※
最頻値は度数が一番大きい値で１つとは限りません。

(2)
池でも陸上トラックでも何でも良いです。

①
\(\,2\,\)周\(\,\mathrm{600\,m}\,\)は毎分\(\,\mathrm{150\,m}\,\)
　\(\hspace{4pt}600\div 150=4　分\)
　\(\hspace{10pt}(\,4\,,\,600\,)\)
\(\,3\,\)分間休んで
　\(\hspace{10pt}(\,7\,,\,600\,)\)
残り\(\,3\,\)周\(\,\mathrm{900\,m}\,\)を毎分\(\,\mathrm{100\,m}\,\)
　\(\hspace{4pt}900\div 100=9　分\)
全部で\(\,5\,\)周したから\(\,16\,\)分で\(\,\mathrm{1500\,m}\,\)走った。
　\(\hspace{10pt}(\,16\,,\,1500\,)\)
これらを原点から直線で結んでいけばグラフができます。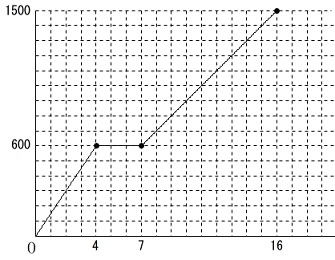
②
\(\,\mathrm{A}\,\)さんの\(\,9\,\)分後のスタートなので
\(\,\mathrm{B}\,\)さんは\(\,\mathrm{800\,m}\,\)遅れてスタートしている。
と考えれば周回遅れは２周分あります。

\(\,\mathrm{B}\,\)さんの方が速いので差を縮めるから
\(\,\mathrm{A}\,\)さんとの差が周回分の
　\(\,600\,,\,300\,,\,0\,\)
となるとき\(\,\mathrm{A}\,\)さんを追い越すことになります。

答え　\(\,\underline{　3　回}\,\)

もう一度追い越すと差は\(\,-300\,\)となりますが、
１分前に走り終わった\(\,\mathrm{B}\,\)さんと\(\,\mathrm{A}\,\)さんとの差は\(\,300\,\)ありません。

グラフで考えるなら交点の数になります。
青線が\(\,\mathrm{A}\,\)さんの位置で赤線が\(\,\mathrm{B}\,\)さんの位置を表します。縦軸は周囲の位置関係を表すので\(\,300\,\)で
スタート地点の\(\,0\,\)に戻ります。

追い越すのはどういうときか考えた方が早いと思いますよ。

第３問

\(\,\large{3}\,\)
図形問題です。

図に分かることを書き込んで行けば良いだけです。

ここだけは少し説明の図を入れますが、
問題にある図に自分で書き込みながら見ていってください。

(1)
\(\,\mathrm{DB=DC}\,\)なので\(\,\mathrm{△DBC}\,\)が二等辺三角形
であることを見逃さなければ
三角形の内角の和で答えはどうやっても出ます。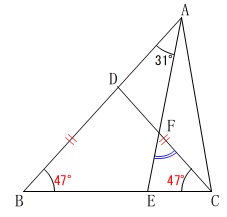\(\,\mathrm{△AEB}\,\)の内角の和は\(\,180°\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AEB}&=&180^{\circ}-(31^{\circ}+47^{\circ})\\
&=&102^{\circ}
\end{eqnarray}\)

よって
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AEB}&=&\mathrm{∠ECF+∠EFC}\\
102^{\circ}&=&47^{\circ}+\mathrm{∠EFC}\\
\mathrm{∠EFC}&=&102^{\circ}-47^{\circ}\\
&=&\underline{　55^{\circ}　}
\end{eqnarray}\)

順序が違いますが
　\(\mathrm{∠FEC=∠EAB+∠EBA}\)
から\(\,\mathrm{△EFC}\,\)の内角の和で求めても良いです。

または
　\(\,\mathrm{∠ADC=94^{\circ}}\,\)
から
\(\,\mathrm{∠EFC}\,\)の対頂角\(\,\mathrm{∠AFD}\,\)を求めても答えは出ます。

大切なのは、
分かる角度を図に書き込んで行くことです。

(2)
条件から合同と相似が見つかります。

条件
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
　\(\,\mathrm{∠ADC}=90^{\circ}\,\)
　\(\,\mathrm{DE:EC=2:1}\,\)
　\(\,\mathrm{AD=2}\,\)
　\(\,\mathrm{BC=DC=6}\,\)
※
これらの条件は図中に書き込みます。
長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。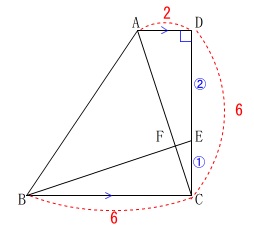ここで\(\,\mathrm{DE:EC=2:1}\,\)なので
　\(\hspace{4pt}\mathrm{DE}=4\,,\,\mathrm{EC}=2\)
\(\,①\,\)
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{EB}&=&\sqrt{\color{blue}{2}^2+\color{red}{6}^2}\\
&=&\sqrt{40}\\
&=&\underline{　2\sqrt{10}　}\mathrm{cm}
\end{eqnarray}\)

②
\(\,\mathrm{△ABF}\,\)の面積ですが
方法はいくつかあるので迷いますね。

公式が利用できない面積や体積は
　\(\,（全体）-（部分）\,\)
を利用することが多いです。

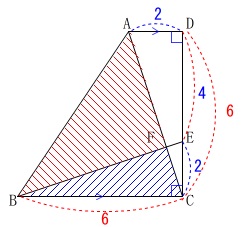
ここでは
　\(\,\mathrm{△ABC-△BFC}\,\)
により\(\,\mathrm{△ABF}\,\)は求まります。

しかし\(\,\mathrm{△ABF}\,\)は直角三角形なので底辺と高さがあります。
　\(\hspace{4pt}\mathrm{△ABF}=\displaystyle \frac{1}{2}\times \mathrm{BF}\times \mathrm{AF}\)

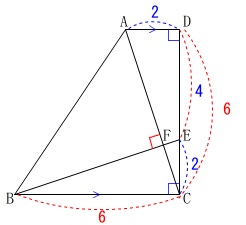
台形からいくつか三角形をひく方法でも良いです。

いずれにしても、
　\(\,\mathrm{△ADC}\,\)≡\(\,\mathrm{△ECB}\,\)
　\(\,\mathrm{△ECB}\,\)∽\(\,\mathrm{△CFB}\,\)∽\(\,\mathrm{△EFC}\,\)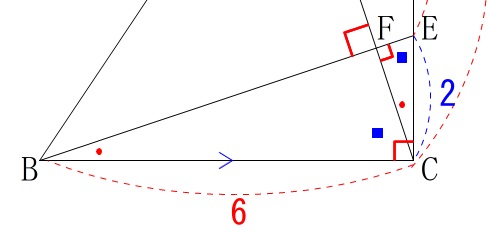
であることは見抜いておきましょう。

相似を利用して部分的な長さを求めておきます。
　\(\,\mathrm{△ECB}\,\)∽\(\,\mathrm{△EFC}\,\)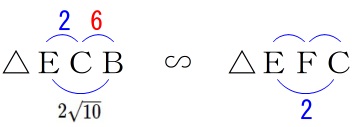なので
　\(\begin{eqnarray}\displaystyle
\mathrm{EC:EF}&=&\mathrm{EB:EC}\\
2:\mathrm{EF}&=&2\sqrt{10}:2\\
2\sqrt{10}\,\mathrm{EF}&=&4\\
\mathrm{EF}&=&\frac{2}{\sqrt{10}}\\
&=&\frac{\sqrt{10}}{5}
\end{eqnarray}\)
また
　\(\begin{eqnarray}\displaystyle
\mathrm{CB:FC}&=&\mathrm{EB:EC}\\
6:\mathrm{FC}&=&2\sqrt{10}:2\\
2\sqrt{10}\,\mathrm{FC}&=&12\\
\mathrm{FC}&=&\frac{6}{\sqrt{10}}\\
&=&\frac{3\sqrt{10}}{5}
\end{eqnarray}\)この後は
　\(\,\mathrm{AC=BE=2\sqrt{10}}\,\)
だから
　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\mathrm{BE-EF}\\
&=&2\sqrt{10}-\frac{\sqrt{10}}{5}\\
&=&\color{magenta}{\frac{9\sqrt{10}}{5}}
\end{eqnarray}\)
および
　\(\begin{eqnarray}\displaystyle
\mathrm{AF}&=&\mathrm{AC-FC}\\
&=&2\sqrt{10}-\frac{3\sqrt{10}}{5}\\
&=&\color{magenta}{\frac{7\sqrt{10}}{5}}
\end{eqnarray}\)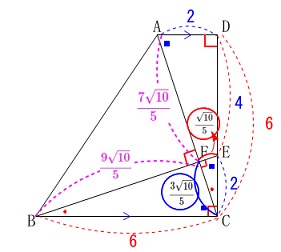直角三角形だから求める\(\,\mathrm{△ABF}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABF}&=&\frac{1}{2}\times \frac{9\sqrt{10}}{5}\times \frac{7\sqrt{10}}{5}\\
&=&\underline{　\frac{63}{5}　}　\mathrm{cm^2}
\end{eqnarray}\)

相似を利用して\(\,\mathrm{F}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろし
\(\,\mathrm{△BFC}\,\)の高さを求め
　\(\,\mathrm{△ABC-△BFC}\,\)
を計算しても良いですが相似を使うのは同じなので
直接\(\,\mathrm{△ABF}\,\)の面積を求めておきました。

※
\(\,\mathrm{F}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろす方法も自分で確認してみてください。

(3)
この問題では長さや面積は比で表されているだけです。

比を一致させる数値なら成り立つので
計算しやすい値を選ぶと楽になります。

条件
　\(\,\mathrm{BD:DC=3:2}\,\)
　\(\,\mathrm{AD}\,\)⊥\(\,\mathrm{BC}\,\)
　\(\displaystyle \,\mathrm{△ABE=\frac{9}{35}\times \,△ABC}\,\)

①
\(\,\mathrm{AE}\,\)の長さは\(\,\mathrm{△ABE}\,\)の底辺とみることができます。

\(\,\mathrm{BD:DC=3:2}\,\)なので\(\,\mathrm{△ABC}\,\)の
　底辺を\(\,5\,\)
（本当は\(\,10\,\)としたいけど分かり易い数字で進めます。）
　高さを\(\,\mathrm{AD}\,\)
とすると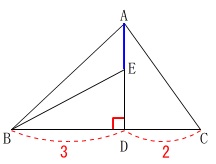
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{AD}\\
&=&\frac{1}{2}\times 5\times \mathrm{AD}\\
&=&\color{red}{\frac{5}{2}\,\mathrm{AD}}
\end{eqnarray}\)
\(\,\mathrm{△ABE}\,\)は底辺が\(\,\mathrm{AE}\,\)で
高さは\(\,\mathrm{BD}\,\)の\(\,3\,\)と見ることができるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&\frac{1}{2}\times \mathrm{AE}\times \mathrm{BD}\\
&=&\frac{1}{2}\times \mathrm{AE}\times 3\\
&=&\color{blue}{\frac{3}{2}\, \mathrm{AE}}
\end{eqnarray}\)

\(\,\mathrm{\color{blue}{△ABE}}\,\)の面積が\(\,\mathrm{\color{red}{△ABC}}\,\)の\(\displaystyle \,\frac{9}{35}\,\)なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{3}{2}\,\mathrm{AE}}:\color{red}{\frac{5}{2}\,\mathrm{AD}}&=&9:35\\
\frac{3}{2}\times 35\times \mathrm{AE}&=&\frac{5}{2}\times 9\times \mathrm{AD}\\
3\times35\times \mathrm{AE}&=&5\times 9\times \mathrm{AD}\\
\mathrm{AE}&=&\frac{5\times 9}{3\times 35}\,\mathrm{AD}\\
&=&\frac{3}{7}\,\mathrm{AD}
\end{eqnarray}\)

答え　\(\displaystyle \underline{　\frac{3}{7}　倍}\)

答えを出すだけなら
\(\,\mathrm{BD:DC=3:2}\,\)なので
\(\,\mathrm{△ABD}\,\)は\(\,\mathrm{△ABC}\,\)の\(\displaystyle \,\frac{3}{5}\,\)倍
\(\,\mathrm{△ABE}\,\)が\(\,\mathrm{△ABC}\,\)の\(\displaystyle \,\frac{9}{35}\,\)になるには
\(\,\mathrm{AE}\,\)は\(\,\mathrm{AD}\,\)の
　\(\hspace{10pt}\displaystyle \frac{9}{35}\div \frac{3}{5}\\
\displaystyle =\frac{9}{35}\times \frac{5}{3}\\
\displaystyle =\frac{3}{7}\)

答え　\(\displaystyle \underline{　\frac{3}{7}　倍}\)

となれば良い、とするのが一番早いです。

\(\,②\,\)
\(\,①\,\)で求めた比の値を利用します。
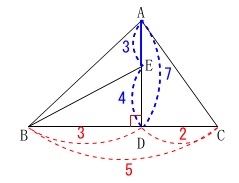体積比なので具体的な長さは必要無く、
比そのものを長さとして計算します。

　\(\,\mathrm{△ABE}\,\)を\(\,\mathrm{AD}\,\)を軸として回転させた体積を\(\,\color{blue}{V_1}\,\)
　\(\,\mathrm{△ADC}\,\)を\(\,\mathrm{AD}\,\)を軸として回転させた体積を\(\,\color{red}{V_2}\,\)
とするとどちらも円錐になるので
（実際には\(\displaystyle \,\frac{1}{3}\,\)や\(\,\pi\,\)は省略します。）
　\(\begin{eqnarray}\displaystyle
\color{blue}{V_1}:\color{red}{V_2}&=&\color{blue}{\frac{1}{3}\times \pi\,(3)^2\times 3}:\color{red}{\frac{1}{3}\times \pi\,(2)^2\times 7}\\
28\,V_1&=&27\,V_2\\
V_1&=&\frac{27}{28}\,V_2
\end{eqnarray}\)

答え　\(\displaystyle \underline{　\frac{27}{28}　倍}\)

\(\,①\,\)が出ていれば軸がどちらも\(\,\mathrm{AD}\,\)であることに注意すれば
\(\,②\,\)の方が分かり易いでしょう。

以上です。

ものすごく手抜きの解説に見えるかもしれませんが、
決して手を抜いたわけではなく、
「実際に手を動かさないと答えは見えてこない。」
ということを実感して欲しいだけです。

この解説は楽だったというのは事実ですけどね。笑

手書きや動画なら編集したとしてももっと楽だろうなあ。
でも、分かった気になるだけで得点には結びつかないからやらない。
（いまのところ）

⇒　２０２１年度愛知県公立校入試Ｂ日程の数学の問題と解説

\(\,\mathrm{B}\,\)日程の問題は普通に解説してあります。
\(\,\mathrm{B}\,\)日程の解説を見てからここに戻って見直してみると
何をやっているのか少しは分かると思います。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

他の年度は詳しく解説しているので傾向ぐらいは見ておくと良いです。