2021年(令和3年)度秋田県公立高校入試の数学の問題と解説

2021年(令和3年)度に秋田県で行われた公立高校入試の数学の問題と解説です。
秋田県における例年通りの数学問題の形式で選択問題があります。
受験する高校によって指定された問題を選択間違いしないように気をつけておきましょう。

2021年（令和3年）度秋田県公立高校入試数学の問題

秋田県立高校の入試数学では選択問題があります。

⇒　2021年（令和3年）度秋田県公立高校入試数学の問題

受験する高校で指定された問題を選択してください。

2021年（令和3年）度秋田県公立高校入試数学の解説

問題の出題項目に変更はありませんが基本中心となっています。
試験時間も十分足りるでしょうから解説もできるだけ短く済ませておきます。

\(\,\large{1}\,\)
選択問題があります。
高校から指定された\(\,8\,\)問を解くようにしてください。

第１問

(1)
　\(\hspace{10pt}4-(-6)\times 2\\
=4+12\\
=\underline{　16　}\)

掛け算部分の計算が先です。

(2)
　\(\hspace{10pt}\displaystyle \frac{x-2y}{2}-\frac{3x-y}{6}\\
\displaystyle =\frac{3(x-2y)-(3x-y)}{6}\\
\displaystyle =\frac{3x-6y-3x+y}{6}\\
\displaystyle =\underline{　\frac{-5y}{6}　}\)

答えの形は\(\hspace{4pt}\displaystyle -\frac{5}{6}\,y\)でも良いですが
通分するときに分子には（かっこ）がついている、
ということを忘れないようにしましょう。

(3)
　\(\hspace{10pt}(x-3y)(x+4y)-xy\\
=x^2+4xy-3xy-12y^2-xy\\
=\underline{　x^2-12y^2　}\)

暗算して間違うより確実に展開しましょう。

(4)
この程度の計算量なら代入しても差はありませんが、、、

　\(\hspace{10pt}a^2+2a\\
=(\sqrt{3}-1)^2+2(\sqrt{3}-1)\\
=3-2\sqrt{3}+1+2\sqrt{3}-2\\
=\underline{　2　}\)

条件式をちょっと変形します。
　\(\begin{eqnarray}\displaystyle
a&=&\sqrt{3}-1\\
a+1&=&\sqrt{3}\end{eqnarray}\)
ここで両辺を２乗して
　\(\begin{eqnarray}\displaystyle
(a+1)^2&=&3\\
a^2+2a+1&=&3\\
a^2+2a&=&\underline{　2　}
\end{eqnarray}\)

会員はこちらの方法でしょう。

(5)
　\(\begin{eqnarray}\displaystyle
\frac{3}{2}x+1&=&10\\
3x+2&=&20\\
3x&=&18\\
x&=&\underline{　6　}
\end{eqnarray}\)

方程式では分数や小数の係数は早いうちになくしておくと良いです。

(6)
紅茶と牛乳を\(\,5:3\,\)に混ぜるのに
あと必要な牛乳を\(\,x\,\)とおいて
　\(\begin{eqnarray}\displaystyle
450:(180+x)&=&5:3\\
5(180+x)&=&450\times 3\\
900+5x&=&1350\\
5x&=&450\\
x&=&\underline{　90　}\,\mathrm{mL}
\end{eqnarray}\)

または、
全体で必要な牛乳を\(\,a\,\)とすると
　\(\begin{eqnarray}\displaystyle
450:a&=&5:3\\
5a&=&450\times 3\\
a&=&270
\end{eqnarray}\)

牛乳は\(\,180\,\)あるので必要な牛乳はあと
　\(\hspace{10pt}270-180\\
=\underline{　90　}\,\mathrm{mL}\)

(7)
連立方程式を解きます。
加減法でも代入法でも差はありません。

　\( \begin{cases}
\hspace{4pt} x+4y=-1　･･･①\\
\hspace{4pt} -2x+y=11　･･･②
\end{cases}\)

加減法で解いておきます。

\(\,①\,\)の両辺を２倍して\(\,②\,\)と辺々加えます。
　\(\hspace{18pt}2x+8y=-2\\
\underline{+)-2x+y=11}\\
\hspace{42pt}9y=9\\
\hspace{46pt}y=1\)
これを\(\,①\,\)に戻すと
（どの方程式でも良いです。）
　\(\begin{eqnarray}\displaystyle
x+4\times (1)&=&-1\\
x&=&-5
\end{eqnarray}\)

答え　\(\,\underline{　x=-5\,,\,y-1　}\,\)

(8)
　\(\hspace{10pt}2x^2-5x+1=0\)

因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{5\pm \sqrt{5^2-4(2)(1)}}{2(2)}\\
&=&\frac{5\pm \sqrt{25-8}}{4}\\
&=&\underline{　\frac{5\pm \sqrt{17}}{4}　}
\end{eqnarray}\)

(9)
代表値の問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

計算すると
　平均値：\(\,4.25\,\)冊
　中央値：\(\,4.5\,\)冊
　最頻値：\(\,5\,\)冊

答え　\(\,\underline{　ウ　}\,\)

ヒストグラムをながめているだけでは読み取りきれませんよ。

(10)
条件を満たす自然数を求めます。
　\(\hspace{4pt}10\,＜\,\sqrt{n}\,＜\,11\)
全辺正の数なので２乗しても大小関係は変わりません。
　\(\hspace{4pt}100\,＜\,n\,＜\,121\)

⇒　ルートのついた無理数の不等式中の整数を表す文字の値を求める方法

この中の自然数で\(\,\sqrt{7n}\,\)を整数にするので
自然数\(\,n\,\)は\(\,7\,\)の倍数です。

　\(\hspace{4pt}n=7\times 15\,,\,7\times 16\,,\,7\times 17\)

このうち\(\,\sqrt{7n}\,\)のルートが外れるのは
　\(\hspace{10pt}n=7\times 16=\underline{　112　}\)

\(\,\sqrt{7n}\,\)のルートが外れるのは
　\(\hspace{10pt}n=7\times k^2\)
となるときで
　\(\hspace{10pt}\displaystyle \sqrt{7n}\\
=\sqrt{7^2\times k^2}\\
=7\times k\)
とルートの中の因数が平方数にならなければなりません。

(11)
三角形の１つの外角です。

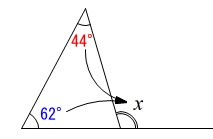
　\(\begin{eqnarray}\displaystyle
x&=&62^{\circ}+44^{\circ}\\
&=&\underline{　106^{\circ}　}
\end{eqnarray}\)

三角形の残りの内角を計算してからでも良いです。

(12)
おうぎ形の面積は公式がありますが、
円の中心角が\(\,360°\,\)であることから
比例計算で求めるだけです。

おうぎ形の面積を\(\,S\,\)とすると
　\(\begin{eqnarray}\displaystyle
S:\pi(5^2)&=&240:360\\
360S&=&25\,\pi\times 240\\
S&=&25\,\pi\times \frac{240}{360}\\
&=&\underline{　\frac{50}{3}\,\pi　}(\mathrm{cm^2})
\end{eqnarray}\)

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

おうぎ形に関する公式は導けますが、
そもそも円や球の公式は導けないので
中学生は公式が覚えられたら使えることが先で良いですよ。

(13)
正三角形に気がつくかどうかです。

　\(\hspace{4pt}\mathrm{AB=OA}\)
なので\(\,\mathrm{△OAB}\,\)は正三角形です。
（円の半径\(\,\mathrm{OB}\,\)も等しい。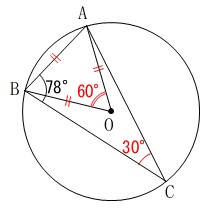）中心角が\(\,\mathrm{∠AOB}=60°\,\)なので
円周角はその半分になるから
　\(\hspace{4pt}\mathrm{∠ACB}=30^{\circ}\)
よって
　\(\begin{eqnarray}\displaystyle
∠ＢＡＣ&=&180^{\circ}-(78^{\circ}+30^{\circ})\\
&=&\underline{　72^{\circ}　}
\end{eqnarray}\)

(14)
回転体はどちらも円錐なので
　底面の円の半径と高さ
だけで比の値は求めることはできます。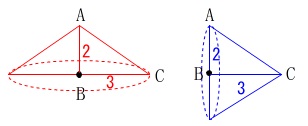
　\(\hspace{10pt}\displaystyle \frac{3^2\times 2}{2^2\times 3}\\
\displaystyle =\frac{18}{12}=\underline{　\frac{3}{2}　}　(倍)\)

体積を求めると
\(\,\mathrm{AB}\,\)を軸とした円錐の体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \pi\,(3^2)\times 2\\
&=&6\,\pi
\end{eqnarray}\)
\(\,\mathrm{BC}\,\)を軸とした円錐の体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \pi\,(2^2)\times 3\\
&=&4\,\pi
\end{eqnarray}\)
これから\(\,V_1\,\)は\(\,V_2\,\)の
　\(\begin{eqnarray}\displaystyle
\frac{V_1}{V_2}&=&\frac{6\,\pi}{4\,\pi}\\
&=&\underline{　\frac{3}{2}　}　(倍)
\end{eqnarray}\)

(15)
立方体の体積が\(\,1000\,\)なので
１辺は\(\,10\,\)となります。
※
単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。

三角錐の体積は底面をどれにしても変わりません。

底面を\(\,\mathrm{△EGH}\,\)と見ると高さは\(\,\mathrm{DH}\,\)です。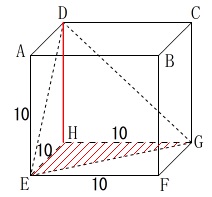三角錐\(\,\mathrm{H-DEG}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{\color{red}{△EGH}}\times \mathrm{DH}\\
&=&\frac{1}{3}\times \color{red}{\frac{1}{2}\times 10^2}\times 10\\
&=&\frac{500}{3}
\end{eqnarray}\)

今度は底面を\(\,\mathrm{△DEG}\,\)と見ます。
\(\,\mathrm{△DEG}\,\)は正三角形で
１辺が正方形の対角線\(\,\color{blue}{10\sqrt{2}}\,\)なので
（三角定規の比\(\,1:2:\sqrt{3}\,\)から）
高さが\(\,\color{red}{5\sqrt{6}}\,\)となるので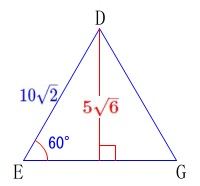\(\,\mathrm{△DEG}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△DEG}&=&\frac{1}{2}\times 10\sqrt{2}\times 5\sqrt{6}\\
&=&25\sqrt{12}\\
&=&\color{magenta}{50\sqrt{3}}
\end{eqnarray}\)

底面\(\,\mathrm{DEG}\,\)から\(\,\mathrm{H}\,\)までの距離を
高さ\(\,\color{red}{h}\,\)とすると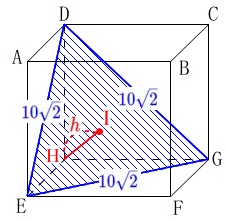三角錐\(\,\mathrm{H-DEG}\,\)の体積\(\,V’\,\)は
　\(\begin{eqnarray}\displaystyle
V’&=&\frac{1}{3}\times \mathrm{△DEG}\times \mathrm{HI}\\
&=&\frac{1}{3}\times \color{magenta}{50\sqrt{3}}\times \color{red}{h}\\
&=&\frac{50\sqrt{3}\,h}{3}
\end{eqnarray}\)

底面を\(\,\mathrm{△EGH}\,\)と見ても\(\,\mathrm{△DEG}\,\)と見ても
三角錐の体積は変わらないから
　\(\begin{eqnarray}
V&=&V’\\
\frac{500}{3}&=&\frac{50\sqrt{3}\,h}{3}\\
h&=&\frac{500}{50\sqrt{3}}\\
&=&\underline{　\frac{10\sqrt{3}}{3}　}　(\mathrm{cm})
\end{eqnarray}\)

ややこしく見えますけど、
実際に自分でやってみると意外とすぐ終わりますよ。

\(\,\large{1}\,\)は以上です。
選択問題を間違えないようにしましょう。

第２問

\(\,\large{2}\,\)
(1)～(4)まであります。

(1)
\(\,①\,\)
反比例の関数の変化の割合を求めます。

関数\(\displaystyle \,y=\frac{6}{x}\,\)において\(\,(\,x\,,\,y\,)\)の値は
\(\,x=1\,\)のとき\(\hspace{2pt}(\,1\,,\,6\,)\)
\(\,x=3\,\)のとき\(\hspace{2pt}(\,3\,,\,2\,)\)
\(\,x\,\)が\(\,1\,\)から\(\,3\,\)まで増加するとき
\(\,x\,\)の増加量は
　\(\hspace{4pt}3-1=2\)
\(\,y\,\)の増加量は
　\(\hspace{4pt}2-6=-4\)
なので変化の割合は
　\(\hspace{10pt}\displaystyle \frac{-4}{2}=\underline{　-2　}\)

変化の割合は関数に関係なく
　\(\hspace{4pt}\displaystyle (変化の割合)=\frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}\)
です。

\(\,②\,\)
比例定数の大小をグラフから読み取る問題です。
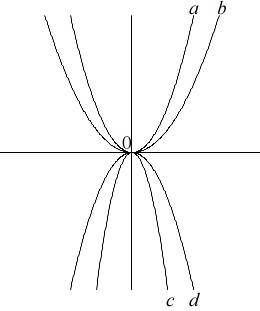下に凸の（上に開いている）場合は分かり易いでしょう。
　\(\hspace{4pt}b\,＜\,a\)

上に凸の（下に開いている）場合は
比例定数が負の数なので注意しましょう。
　\(\hspace{4pt}c\,＜\,d\)

正の数の方が大きい数なので
　\(\hspace{4pt}c\,＜\,d\,＜\,b\,＜\,a\)

答え　\(\,\underline{　エ　}\,\)

(2)
\(\,①\,\)
６行目まで書き出せば確実に答えが出ます。
　\(\begin{array}{|c|c|c|c|c|} \hline
1 & 2 & 3 & 4 & 5 \\ \hline
10 & 9 & 8 & 7 & 6 \\ \hline
11 & 12 & 13 & 14 & 15 \\ \hline
20 & 19 & 18 & 17 & 16 \\ \hline
21 & 22 & 23 & 24 & 25 \\ \hline
\color{red}{30} & 29 & 28 & 27 & 26 \\ \hline
\end{array}\)　

答え　\(\,\underline{　30　}\,\)

１行で５ずつ増えるので
６行目（偶数行）の１列目は\(\,10\,\)の倍数です。
　\(\hspace{4pt}5\times 6=30\)

\(\,②\,\)
左から増えようが右から増えようが
\(\,3\,\)列目は１つ上の数より\(\,+5\,\)となります。
　\(\begin{array}{|c|c|c|c|c|} \hline
1 & 2 & \color{red}{3} & 4 & 5 \\ \hline
10 & 9 & \color{red}{8} & 7 & 6 \\ \hline
11 & 12 & \color{red}{13} & 14 & 15 \\ \hline
20 & 19 & \color{red}{18} & 17 & 16 \\ \hline
21 & 22 & \color{red}{23} & 24 & 25 \\ \hline
: & : & : & : & : \\ \hline
\end{array}\)

\(\,n\,\)行目までは最初の\(\,3\,\)から
\(\,+5\,\)が\(\,(\,n-1\,)\,\)回増えるので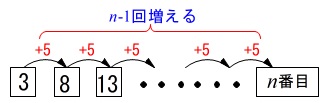
　\(\hspace{10pt}3+5(n-1)\\
=\underline{　5n-2　}\)

(3)
点\(\,\mathrm{P}\,\)の作図です。

満たす条件は
　\(\,\mathrm{ＡＢ⊥ＣＤ}\,\)
　\(\,\mathrm{∠ＢＣＤ=∠ＢＰＤ}\,\)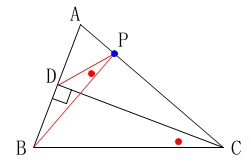
\(\,\mathrm{ＡＢ⊥ＣＤ}\,\)から
　\(\hspace{4pt}\mathrm{∠BDC}=90^{\circ}\)
なので
　線分\(\,\mathrm{BC}\,\)が円の直径
かつ
　\(\hspace{4pt}\,\mathrm{∠ＢＣＤ=∠ＢＰＤ}\,\)
から
　４点\(\,\mathrm{B\,,\,C\,,\,P\,,\,D}\,\)が同じ円周上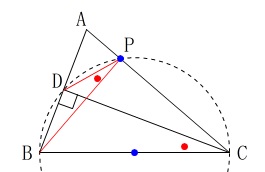にあれば良いので
　線分\(\,\mathrm{BC}\,\)の中点を中心とする円
を描きます。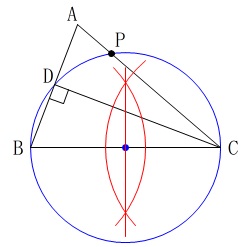線分\(\,\mathrm{BC}\,\)の垂直二等分線と\(\,\mathrm{BC}\,\)の交点が円の中心です。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

作図で使う手法はおおよそ決まっています。

(4)
道のり、速さ、時間の関係の立式です。

条件
　\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)を通って\(\,\mathrm{G}\,\)まで\(\,30\,\mathrm{km}\)
　\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)まで時速\(\,12\,\mathrm{km}\,\)
　\(\,\mathrm{R}\,\)から\(\,\mathrm{G}\,\)まで時速\(\,9\,\mathrm{km}\,\)
　\(\,\mathrm{S}\,\)から\(\,\mathrm{G}\,\)まで\(\,3\,\)時間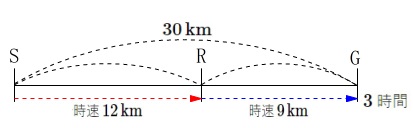二通りの方程式の立て方ができます。
※
途中では単位\(\,\mathrm{km}\,\)を省略します。

１つは道のりを\(\,x\,,\,y\,\)とする方法。

　\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)までの道のりを\(\,x\,\)
　\(\,\mathrm{R}\,\)から\(\,\mathrm{G}\,\)までの道のりを\(\,y\,\)
とすると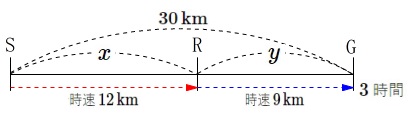道のり\(\,\mathrm{S}\,\)から\(\,\mathrm{G}\,\)までは\(\,30\,\)なので
　\(\hspace{10pt}x+y=30\)
また、時間は道のりを速さで割った商なので
\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)までの所要時間は\(\displaystyle \frac{x}{12}\)
\(\,\mathrm{R}\,\)から\(\,\mathrm{G}\,\)までの所要時間は\(\displaystyle \frac{y}{12}\)
全体でかかった時間は\(\,3\,\)時間だから
　\(\hspace{10pt}\displaystyle \frac{x}{12}+\frac{y}{9}=3\)

連立すると
　\( \begin{cases}
\hspace{4pt} x+y=\color{black}{\fbox{　30　}}\\
\hspace{4pt} \color{black}{\fbox{ 　\(\displaystyle\,\frac{x}{12}+\frac{y}{9}\,\)　}}=3
\end{cases}\)

もう一つは時間を\(\,x\,,\,y\,\)とする方法。

　\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)までかかった時間を\(\,x\,\)
　\(\,\mathrm{R}\,\)から\(\,\mathrm{G}\,\)までかかった時間を\(\,y\,\)
とすると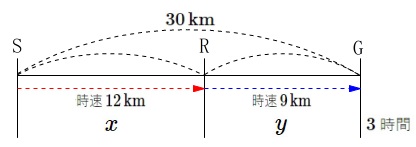\(\,\mathrm{S}\,\)から\(\,\mathrm{G}\,\)までかかった時間は\(\,3\,\)時間なので
　\(\hspace{10pt}x+y=3\)
また、道のりは速さと時間の積なので
\(\,\mathrm{S}\,\)から\(\,\mathrm{R}\,\)までの距離は\(\,12x\,\)
\(\,\mathrm{R}\,\)から\(\,\mathrm{G}\,\)までの距離は\(\,9y\,\)
\(\,\mathrm{S}\,\)から\(\,\mathrm{G}\,\)までの距離は\(\,30\,\)だから
　\(\hspace{10pt}\displaystyle 12x+9y=30\)

連立すると
　\( \begin{cases}\displaystyle
\hspace{4pt} x+y=\color{black}{\fbox{　3　}}\\
\hspace{4pt} \color{black}{\fbox{　\(\,12x+9y\,\)　}}=30
\end{cases}\)

立式だけが問題になっているので解く必要はありません。
文字が表しているものは違うので
それぞれ解いた\(\,x\,,\,y\,\)は違う値になります。

第３問

平行線と図形の問題です。

(1)
相似の証明です。

条件は
　\(\,\mathrm{DE}\,\)∥\(\,\mathrm{BC}\,\)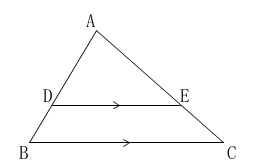平行線の同位角と錯角は等しくなり、
さらに\(\,\mathrm{∠A}\,\)は共通な角でもあります。相似の証明には条件が余りますので
証明に示す相似条件は分かれますね。

相似条件は
　「２組の角がそれぞれ等しい。」
で同じです。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ADE}\,\)において
\(\,\mathrm{DE}\,\)∥\(\,\mathrm{BC}\,\)だから同位角が等しいので
　\(\hspace{4pt}\mathrm{∠ABC=∠ADE}　･･･①\)
　\(\hspace{4pt}\mathrm{∠ACB=∠AED}　･･･②\)
\(\,①\,②\,\)より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ADE}\,\)
（終わり）

\(\,①\,\)または\(\,②\,\)の代わりに
　\(\,\mathrm{∠A}\,\)が共通　\(\,･･･③\,\)
でも良いです。

(2)
四角形と平行線の性質です。

条件
　\(\,\mathrm{AE\,=\,EB}\,\)
　\(\,\mathrm{BF\,=\,FC}\,\)
　\(\,\mathrm{EH}\,\)∥\(\,\mathrm{BD}\,\)
　\(\,\mathrm{FG}\,\)∥\(\,\mathrm{BD}\,\)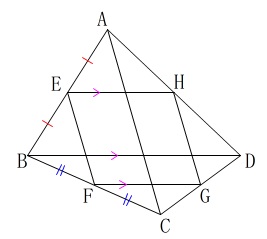四角形\(\,\mathrm{ABCD}\,\)の形に関係なく
四角形\(\,\mathrm{EFGH}\,\)は平行四辺形になります。

証明に利用される定理は
　「中点連結定理」
です。

\(\,①\,\)
詩織さんの証明で書かれていることは
　\(\displaystyle \mathrm{EH=FG=\frac{1}{2}\,BD}\)
　\(\,\mathrm{EH}\,\)∥\(\,\mathrm{FG}\,\)∥\(\,\mathrm{BD}\,\)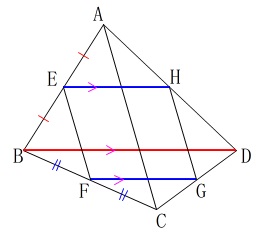平行四辺形である条件は
　「１組の対辺が平行で等しい。」
または
　「１組の対辺が等しく平行である。」
です。

記号ばかりでわかりにくいかもしれませんが、
図の中で確認すれば難しくはありません。

※
辺について「等しい」とは長さのことなので
「長さが等しい」と「等しい」は同じ意味になります。

\(\,②\,\)
ひし形になることの証明です。

\(\,①\,\)で利用した条件に加えて、
ひし形になる条件を選びます。

ひし形は
　「４つの辺がすべて等しい平行四辺形」
と言い換えることができます。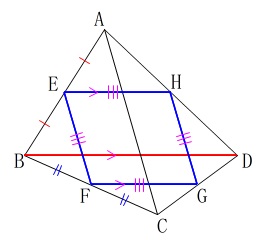\(\,①\,\)と同じように中点連結定理を利用すると
　\(\displaystyle \mathrm{EF=HG=\frac{1}{2}\,AC}\)

このとき
　\(\,\mathrm{AC=BD}\,\)
であれば４つの辺が等しい平行四辺形になります。

もう一つ
「対角線が直交する平行四辺形」
という条件でもひし形はいえますがここではありません。

この条件の中では、
四角形\(\,\mathrm{ABCD}\,\)の対角線が等しいときにひし形になります。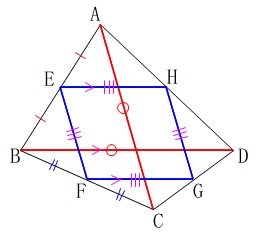つまり
　\(\hspace{4pt}\mathrm{AC=BD}\)

答え　\(\,\underline{　エ　}\,\)

(3)
四角形の面積を求めます。

これは簡単なので説明を少なく終わらせておきます。
ただし、
問題文にある条件は図示しておかなければ
おそらくわかりにくい問題です。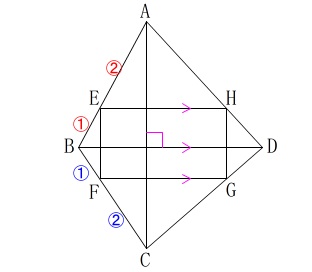四角形\(\,\mathrm{ABCD}\,\)の面積は\(\,18\,\mathrm{cm^2}\)ですが、
辺の長さの条件はありません。
※
途中では単位を省略します。

だから\(\,\mathrm{AC=BD=6}\,\)としても問題はありません。

こういう具体的な数値なら辺の比から
　\(\,\mathrm{EF=2\,,\,EH=4}\,\)
となるので四角形\(\,\mathrm{EFGH}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{EF}\times \mathrm{EH}\\
&=&2\times 4\\
&=&\underline{　8　}　(\mathrm{cm^2})
\end{eqnarray}\)
と答えを出すことは簡単でしょう。

雑すぎるといわれそうなので（笑）
少し一般的に説明しておきます。
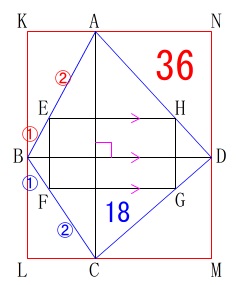\(\,\mathrm{AC\,,\,BD}\,\)に平行な線分によってできる
長方形\(\,\mathrm{KLMN}\,\)の面積は\(\,\color{red}{36}\,\)になります。

問題の条件の辺の比から
　\(\hspace{4pt}\displaystyle \mathrm{EF=\frac{1}{3}\,AC=\frac{1}{3}\,KL}\)
　\(\hspace{4pt}\displaystyle \mathrm{EH=\frac{2}{3}\,BD=\frac{2}{3}\,KN}\)

よって求める四角形\(\,\mathrm{EFGH}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&36\times \frac{1}{3}\times \frac{2}{3}\\
&=&\underline{　8　}　(\mathrm{cm^2})
\end{eqnarray}\)

他にも四角形\(\,\mathrm{ABCD}\,\)からでも答えは出せます。
「数学の解法は１つではない。」
ということが分かっていればそれでいいです。

第４問

(1)確率(2)文字式による証明の２題です。

(1)
５個の玉から２個を取り出す確率ですが
\(\,①\,\)と\(\,②\,\)で取り出し方が違うので注意しましょう。

袋の中に\(\,1\,\)～\(\,5\,\)の数字が１つずつ書かれた玉が５個入っています。

\(\,①\,\)
初めに取り出した玉に書かれた数字を\(\,x\,\)とし、
取り出した玉を袋に戻しもう一回取り出します。
２回目に捕りだした球を\(\,y\,\)とします。

このとき\(\,\color{red}{x}\,＞\,\color{blue}{y}\,\)となる確率を求めます。

樹形図で良いです。
ここでは表で見ておきます。
※
赤数字が１回目に取り出した数字\(\,\color{red}{x}\,\)
青数字が２回目に取り出した数字\(\,\color{blue}{y}\,\)です。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} \\ \hline
\color{blue}{1} & & ○ & ○ & ○ & ○\\ \hline
\color{blue}{2} & & & ○ & ○ & ○\\ \hline
\color{blue}{3} & & & & ○ & ○\\ \hline
\color{blue}{4} & & & & & ○\\ \hline
\color{blue}{5} & & & & & \\ \hline
\end{array}\)

玉を元に戻すので２回目も同じ数字があり得ます。

\(\,\color{red}{x}\,＞\,\color{blue}{y}\,\)となるのは
　\(\displaystyle \frac{10}{25}=\frac{2}{5}\)

答え　\(\displaystyle \underline{　\frac{2}{5}　}\)

\(\,②\,\)
同時に２個の玉を取り出し、
少なくとも１個に偶数が書かれている確率を求めます。

同時に玉を取り出すのも
１個ずつ２個取り出すのも同じです。

ただしこの場合は
１回目に取り出した玉は戻しませんので
同じ数字は出てきません。

　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} \\ \hline
\color{blue}{1} & × & & & & \\ \hline
\color{blue}{2} & & × & & & \\ \hline
\color{blue}{3} & & & × & & \\ \hline
\color{blue}{4} & & & & × & \\ \hline
\color{blue}{5} & & & & & ×\\ \hline
\end{array}\)
２個の玉の組み合わせは２０通りあります。
このうち少なくとも１個偶数が含まれるのは
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} \\ \hline
\color{blue}{1} & × & ○ & & ○ & \\ \hline
\color{blue}{2} & ○ & × & ○ & ○ & ○\\ \hline
\color{blue}{3} & & ○ & × & ○ & \\ \hline
\color{blue}{4} & ○ & ○ & ○ & × & ○\\ \hline
\color{blue}{5} & & ○ & & ○ & ×\\ \hline
\end{array}\)
１４通りあるので求める確率は
　\(\displaystyle \frac{14}{20}=\underline{　\frac{7}{10}　}\)

多くの場合「『少なくとも』１個が偶数」と問題にある場合は
「両方が奇数」（余事象）の確率を１から引くことで求めます。

両方奇数となるのは
　\(\displaystyle \frac{6}{20}=\frac{3}{10}\)
なので
　\(\hspace{4pt}\displaystyle 1-\frac{3}{10}=\underline{　\frac{7}{10}　}\)

この問題は場合が少ないのでどちらでも良いですが
元に戻すのか、戻さないのかは間違えないようにしましょう。

(2)
説明の続きを書くだけなのでうめておきます。

［説明］
　３けたの自然数の百の位の数を\(\,a\,\)、
十の位の数を\(\,b\,\)、
一の位の数を\(\,c\,\)とすると、
３けたの自然数は\(\,100a+10b+c\,\)と表すことができる。
各位の数の和を引くと
\(\color{black}{\fbox{　\(\hspace{10pt}100a+10b+c-(a+b+c)　　　\\
=99a+9b\\
=9(11a+b)\\
ここで\\
\,11a+b\,は自然数なので\\
これは\,9\,の倍数である。　\)}}\)
したがって、３けたの自然数から、
その数の各位の数をひくと、９の倍数になる。
（説明ここまで）

「\(\,11a+b\,\)は自然数なので」としましたが
「整数なので」でも良いですよ。
自然数で倍数になるということは整数でも倍数になります。

第５問（選択問題）

\(\,\large{5}\,\)
この問題は受験する高校側から指示された問題を答えることになります。

\(\,\mathrm{Ⅰ\,,\,Ⅱ}\,\)とも関数の問題です。

５－Ⅰ

\(\,Ⅰ\,\)

条件
　\(\,\mathrm{A\,(\,8\,,\,0\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,3\,)}\,\)
　直線\(\,㋐\,\)は\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)を通る。
　直線\(\,㋑\,\)は\(\,2\,\)点\(\,\mathrm{O\,,\,B}\,\)を通る。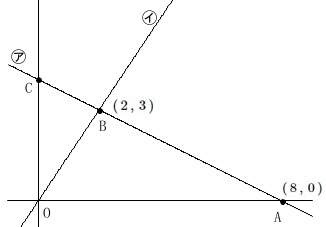
(1)
線分\(\,\mathrm{AB}\,\)の長さを求めます。

長さの単位は\(\,\mathrm{cm}\,\)です。
座標間の距離に\(\,\mathrm{cm}\,\)をつければ良いだけですよ。

　\(\,\mathrm{A\,(\,8\,,\,0\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,3\,)}\,\)
なので\(\,2\,\)点間の距離の公式から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB}&=&\sqrt{(8-2)^2+(0-3)^2}\\
&=&\sqrt{6^2+3^2}\\
&=&\sqrt{36+9}\\
&=&\sqrt{45}\\
&=&\underline{　3\sqrt{5}　}　(\mathrm{cm})
\end{eqnarray}\)

または三平方の定理から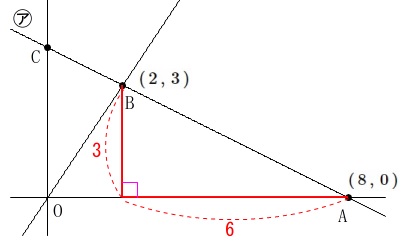
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2}&=&3^2+6^2\\
&=&9+36\\
&=&45
\end{eqnarray}\)
長さなので正の平方根を取って
　\(\hspace{10pt}\displaystyle \mathrm{AB}=\underline{　3\sqrt{5}　}　(\mathrm{cm})\)
でも良いです。

\(\,2\,\)点間の距離の公式は
座標上で三平方の定理を使って導き出しますのでどちらも同じです。

(2)
直線\(\,㋐\,\)、つまり２点\(\,\mathrm{A\,,\,B}\,\)を通る直線の式を求めます。

　\(\,\mathrm{A\,(\,8\,,\,0\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,3\,)}\,\)

（解答例）
２点\(\,\mathrm{A\,,\,B}\,\)を通る直線は軸に平行ではないので
１次関数になり傾きは
　\(\hspace{4pt}\displaystyle \frac{3-0}{2-8}=-\frac{1}{2}\)
これから求める直線は
　\(\hspace{4pt}\displaystyle y=-\frac{1}{2}\,x+b\)
とおける。
これが\(\,\mathrm{A}\,\)を通るので代入して
　\(\begin{eqnarray}\displaystyle
0&=&-\frac{1}{2}\,(8)+b\\
b&=&4
\end{eqnarray}\)
よって求める直線の式は
　\(\hspace{10pt}\displaystyle \underline{　y=-\frac{1}{2}\,x+4　}\)

※
\(\,y\,\)切片\(\,b\,\)を求めるのに点\(\,\mathrm{A}\,\)を代入しましたが
もちろん点\(\,\mathrm{B}\,(\,2\,,\,3\,)\)を代入してもいいですよ。
　\(\begin{eqnarray}\displaystyle
3&=&-\frac{1}{2}\,(2)+b\\
b&=&4
\end{eqnarray}\)

(3)
三角形の面積を等しくする点の座標を求めます。

　\(\,\mathrm{△COP\,=\,△BAP}\,\)
となる点\(\,\mathrm{P}\,\)の\(\,x\,\)座標です。
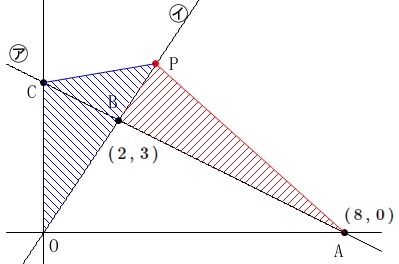点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は
\(\,2\,\)より大きいので点\(\,\mathrm{B}\,\)より右です。

直線\(\,㋑\,\)は２点\(\,\mathrm{O\,,\,B}\,\)を通るので
　\(\hspace{10pt}\displaystyle y=\frac{3}{2}\,x\)
とおけるので求める点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
　\(\displaystyle \,\mathrm{P}\,\left(\,t\,,\,\frac{3}{2}\,t\,\right)\,\)

\(\,\mathrm{△COP}\,\)と\(\,\mathrm{△BAP}\,\)の面積を直接計算できる人は限られるので
（『覚え太郎』会員は途中過程いらないので使って良いですが、
この程度で使う必要もありません。）
軸に平行な線分を底辺と高さにとって引き算します。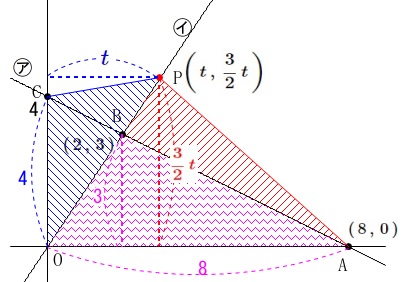
\(\,\mathrm{△COP}\,\)は底辺が直線\(\,㋐\,\)の\(\,y\,\)切片から\(\,\mathrm{OC=4}\,\)、
高さが点\(\,\mathrm{P}\,\)の\(\,x\,\)座標\(\,t\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△COP}&=&\frac{1}{2}\times \color{blue}{4}\times \color{blue}{t}\\
&=&2t
\end{eqnarray}\)

\(\,\mathrm{△BAP}\,\)の面積は\(\,\mathrm{△OAP}\,\)から\(\,\mathrm{△OAB}\,\)を引けば良いので
　\(\begin{eqnarray}\displaystyle
\mathrm{△BAP}&=&\mathrm{△OAP-△OAB}\\
&=&\frac{1}{2}\times \color{magenta}{8}\times \color{red}{\frac{3}{2}\,t}-\frac{1}{2}\times \color{magenta}{8}\times \color{magenta}{3}\\
&=&6t-12
\end{eqnarray}\)

\(\,\mathrm{△COP=△BAP}\,\)のとき
　\(\begin{eqnarray}\displaystyle
2t&=&6t-12\\
t&=&3
\end{eqnarray}\)

答え　\(\,\underline{　3　}\,\)

\(\,\mathrm{△BAP}\,\)の形だと面積の公式は普通の中学生は知りません。
公式がない面積や体積を求めるときは
　\(\,（部分）＋（部分）\,\)
または
　\(\,（全体）－（部分）\,\)
で求めるのが基本となります。

５－Ⅱ

\(\,\mathrm{Ⅱ}\,\)
こちらも関数の直線の式、座標を求める問題です。

条件
　\(\,\mathrm{A}\,(\,3\,,\,4\,)\,\)
　\(\,\mathrm{B}\,(\,0\,,\,3\,)\,\)
　直線\(\,㋐\,\)は\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)を通る。
　直線\(\,㋑\,\)は\(\,y=3x-5\,\)
　点\(\,\mathrm{C}\,\)は\(\,㋑\,\)と\(\,x\,\)軸との交点
　点\(\,\mathrm{D}\,\)は直線\(\,㋑\,\)と\(\,y\,\)軸との交点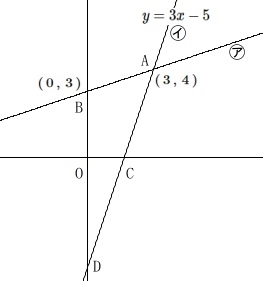
(1)
\(\,2\,\)点\(\,\mathrm{B\,,\,C}\,\)を通る直線の式を求めます。

点\(\,\mathrm{C}\,\)は\(\,y=3x-5\,\)と\(\,x\,\)軸との交点なので
\(\,x\,\)軸\(\,y=0\,\)と連立することで
　\(\,\displaystyle \mathrm{C}\,\left(\,\frac{5}{3}\,,\,0\,\right)\)
点\(\,\mathrm{B}\,\)は
　\(\,\mathrm{B}\,(\,0\,,\,3\,)\,\)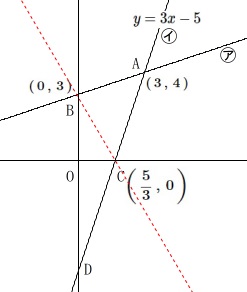なので\(\,2\,\)点\(\,\mathrm{B\,,\,C}\,\)を直線の式は\(\,1\,\)次関数になり
\(\,y\,\)軸との交点\(\,\mathrm{B}\,\)から
　\(\hspace{4pt}\displaystyle y=ax+3\)
とおけて点\(\,\mathrm{C}\,\)を通るので代入して
　\(\begin{eqnarray}\displaystyle
0&=&a\times \frac{5}{3}+3\\
\frac{5}{3}a&=&-3\\
a&=&-3\times \frac{3}{5}\\
&=&-\frac{9}{5}
\end{eqnarray}\)
よって求める直線の式は
　\(\hspace{10pt}\displaystyle y=-\frac{9}{5}\,x+3\)

※
\(\,2\,\)点\(\,(\,a\,,\,0\,)\,,\,(\,0\,,\,b\,)\,\)を通る直線は
　\(\hspace{10pt}\displaystyle \frac{x}{a}+\frac{y}{b}=1\)
となるので点\(\,\mathrm{C}\,\)が分かれば
　\(\begin{eqnarray}\displaystyle
\frac{x}{\frac{5}{3}}+\frac{y}{3}&=&1\\
\frac{3}{5}\,x+\frac{y}{3}&=&1\\
\end{eqnarray}\)
としても良いです。

(2)
点\(\,\mathrm{P}\,\)は直線\(\,㋑\,\)上の\(\,x\,\)座標が正の点です。

\(\,①\,\)
\(\,\mathrm{BD＝PD}\,\)となる点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。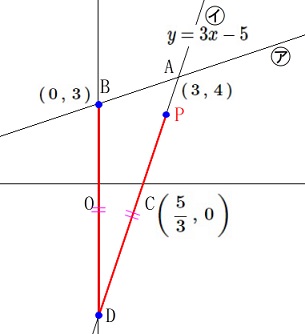点\(\,\mathrm{P}\,\)は中心\(\,\mathrm{D}\,\)、半径\(\,\mathrm{BD}\,\)の円周上にありますが、
単純に\(\,2\,\)点間の距離（三平方の定理）で求めましょう。

点\(\,\mathrm{P}\,\)は\(\,y=3x-5\,\)上の点なので
　\(\,\mathrm{P}\,(\,t\,,\,3t-5\,)\)
点\(\,\mathrm{D}\,\)は\(\,y=3x-5\,\)の\(\,y\,\)軸との交点なので
　\(\,\mathrm{D}\,(\,0\,,\,-5\,)\)このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{PD}^2&=&(t-0)^2+\{(3t-5)-(-5)\}^2\\
&=&10\,t^2
\end{eqnarray}\)
また\(\,\mathrm{BD＝8}\,\)なので
　\(\hspace{4pt}\mathrm{BD}^2=64\)
\(\,\mathrm{BD=PD}\,\)のとき\(\,\mathrm{BD^2=PD^2}\,\)だから
　\(\begin{eqnarray}\displaystyle
10t^2&=&64\\
t^2&=&\frac{64}{10}\\
t&=&\pm \frac{8}{\sqrt{10}}\\
&=&\pm \frac{4\sqrt{10}}{5}
\end{eqnarray}\)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は正なので
　\(\hspace{4pt}\displaystyle t=\frac{4\sqrt{10}}{5}\)

答え　\(\,\underline{　\displaystyle \frac{4\sqrt{10}}{5}　}\,\)

もちろんですが、
\(\,\mathrm{BD=PD}\,\)のままルートを残して計算しても良いですよ。
両辺平方したら同じなので
\(\,8=\sqrt{64}\,\)として両辺のルートの中身が等しいと処理していいです。

\(\,②\,\)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,3\,\)より大きいときに、
直線\(\,\mathrm{OP}\,\)と直線\(\,㋐\,\)の交点を\(\,\mathrm{Q}\,\)とするとき
\(\,\mathrm{△OBQ}\,\)と\(\,\mathrm{△APQ}\,\)の面積が等しくなる点\(\,\mathrm{P}\,\)の座標を求めます。

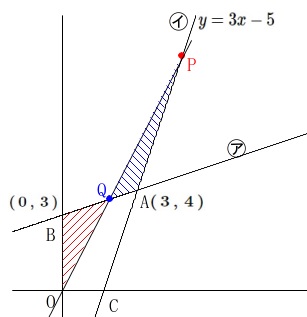
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,3\,\)より大きいのは
座標上で点\(\,\mathrm{A}\,\)より右のときです。

底辺としても高さとしても共通の辺がないので、
\(\,2\,\)点\(\,\mathrm{O\,,\,A}\,\)を結んで共通の辺を作りましょう。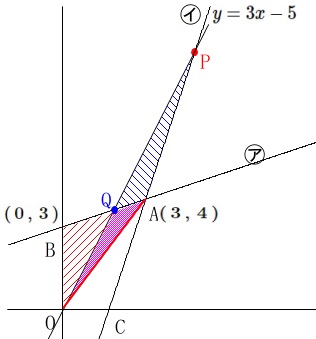
すると\(\,\mathrm{△OAQ}\,\)は共通部分になるので
　\(\,\mathrm{△OAB=△OAP}\,\)
になれば
　\(\,\mathrm{△OBQ=△APQ}\,\)
がいえます。

このとき\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△OAP}\,\)は
辺\(\,\mathrm{OA}\,\)を共通の底辺としているので
　\(\,\mathrm{OA}\,\)∥\(\,\mathrm{BP}\,\)
となれば条件を満たします。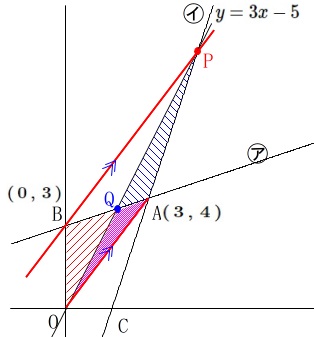直線\(\,\mathrm{OA}\,\)の傾きは\(\,\displaystyle \frac{4}{3}\,\)なので
直線\(\,\mathrm{BP}\,\)の式は\(\,y\,\)軸との交点が\(\,(\,0\,,\,3\,)\,\)なので
　\(\hspace{4pt}\displaystyle y=\frac{4}{3}\,x+3\)
この直線と\(\,㋑\,\)の直線\(\,y=3x-5\,\)との交点が
点\(\,\mathrm{P}\,\)なので連立すると
右辺どうしが等しいことから
　\(\begin{eqnarray}\displaystyle
\frac{4}{3}\,x+3&=&3x-5\\
4x+9&=&9x-15\\
-5x&=&-24\\
x&=&\frac{24}{5}
\end{eqnarray}\)

これが求める点\(\,\mathrm{P}\,\)の\(\,x\,\)座標です。

答え　\(\displaystyle x=\underline{　\frac{24}{5}　}\)
　
求めるのは\(\,x\,\)座標だけなので以上です。

⇒　秋田県の公立高校入試数学の過去問と解説

秋田県立高校入試の数学問題は少しの応用はありますが
毎年基本を幅広く、偏りのない問題構成になっています。

十分満点が狙えるので過去問で確認しておいてください。
解説は過去の年度ほどていねいにやっています。笑