２０２１年度愛知県公立校入試Ｂ日程の数学の問題と解説

２０２１年（令和３年）度愛知県公立校入試Ｂ日程の数学の問題と解説です。
Ｂグループの数学もＡグループと同様の問題構成で、
大問３問ですが基本から応用まで広い範囲の出題ですので手を抜いて良い分野はありません。
応用されている問題は詳しく解説していきます。

２０２１年度愛知県公立高校入試Ｂ日程の数学の問題

大問が３つあります。

⇒　2021年（令和3年）度愛知県公立高校入試Ｂ日程の数学の問題

試験時間に対し、問題数としては少なくはありません。

２０２１年度愛知県公立高校入試Ｂ日程の数学の解説

２０２１年度Ａ日程の数学では力をつけてもらう目的で
図やグラフを入れず解説をほとんどしていませんが、
ここでは少し解説を増やしておきます。

ただし、自分で手を動かさないと見えてこない問題も多くあります。
分かった気になる程度で終わらせないためにも
ノートなどに自分で処理して確かめながら読み進めると良いですよ。

第１問

\(\,\large{1}\,\)
(1)～(10)までの小問題集合です。

計算問題ばかりではありませんが、
十分な基礎をおさえて確実に得点したいところです。

(1)
　\(\hspace{10pt}3-7\times (5-8)\\
=3-7\times (-3)\\
=3+21\\
=\underline{　24　}\)

引き算より掛け算が先ですが
（かっこ）の中から先に処理します。

(2)
　\(\hspace{10pt}27x^2y\div (-9xy)\times (-3x)\\
\displaystyle =\frac{27x^2y\times 3x}{9xy}\\
=\underline{　9x^2　}\)

先ずは全体の符号を確認し、
\(\,\div\,\)の直後は分母にして約分します。

(3)
　\(\hspace{10pt}\sqrt{48}-3\sqrt{6}\div \sqrt{2}\\
=4\sqrt{3}-3\sqrt{3}\\
=\underline{　\sqrt{3}　}\)

足し算引き算より掛け算割り算が先なのは変わりません。
無理数の計算では素因数分解は確実にしましょう。

⇒　素数とは？素因数分解の方法と平方根の求め方(ルートの使い方準備)　

ルートの中身どうしは割り算できます。

(4)
因数分解します。
展開ではないので間違えないようにしてください。

　\(\hspace{10pt}(x+1)(x-8)+5x\\
=x^2-7x-8+5x\\
=x^2-2x-8\\
=\underline{　(x+2)(x-4)　}\)

公式のない因数分解はあれこれ考えるより
一度展開して整理すると機械的にできるようになります。

(5)
方程式を解きます。
「方程式を解く」と「方程式の解を求める」は同じ意味です。

　\(\begin{eqnarray}\displaystyle
(x+2)^2&=&7\\
x+2&=&\pm \sqrt{7}\\
x&=&\underline{　-2\pm \sqrt{7}　}
\end{eqnarray}\)

左辺を展開して
　\(\begin{eqnarray}\displaystyle
x^2+4x+4&=&7\\
x^2+4x-3&=&0
\end{eqnarray}\)
この後解の公式でも良いですが、
せっかくまとまりを作ってくれているので利用しましょう。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

解の公式は問題の形に変形することで導かれています。

(6)
変わらないのはあめの個数です。

\(\,10\,\)人に\(\,b\,\)個ずつ配ると配ったあめは
　\(\hspace{4pt}10\,b\,\)個
余りが\(\,c\,\)個なので
　\(\hspace{10pt}\underline{　a-10b=c　}\)

あめの総数は変化しないので
　\(\hspace{10pt}\underline{　a=10b+c　}\)
とするのが自然でしょうか。

関係式としては同じなのでどちらでも構いません。

(7)
代表値に関する問題です。

代表値は小学校の算数の内容になるので
いつまで出題されるかは分かりませんが、
データを扱う上では大切な項目です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

基本通り\(\,8\,\)人のデータを小さい順に並べます。
　\(\hspace{4pt}42\,,\,45\,,\,45\,,\,49\,,\,50\,,\,51\,,\,53\,,\,57\)

正しい記号を「すべて選ぶ」のですべて求めておきましょう。

\(\,ア\,\)
平均値はデータの合計を度数の合計で割れば出てきます。
　\(\hspace{4pt}\displaystyle \color{red}{49}\,回\)（正しい）

\(\,イ\,\)
中央値は\(\,4\,\)番目と\(\,5\,\)番目の値の平均値になるので
　\(\hspace{4pt}49.5\,回\)（正しくない）

\(\,ウ\,\)
最頻値は\(\,45\,回\,\)だけです。（正しくない）

\(\,57\,\)回は最大値です。

\(\,エ\,\)
範囲は最大値と最小値との差なので
　\(\hspace{4pt}57-42=\color{red}{15}\,回\,\)（正しい）

答え　\(\,\underline{　ア\,,\,エ　}\,\)

平均値を求めるときは
最頻値や中央値に近い値を\(\,0\,\)とし、
\(\,42\,,\,45\,,\,45\,,\,49\,,\,\color{red}{50}\,,\,51\,,\,53\,,\,57\)
を
\(\,-8\,,\,-5\,,\,-5\,,\,-1\,,\,\color{red}{0}\,,\,+1\,,\,+3\,,\,+7\)
としてこの平均値
　\(\displaystyle \frac{-8}{8}=-1\)
が\(\,0\,\)とおいた\(\,50\,\)とのズレとして
平均値を求めると小さい数字で計算できますが、
これくらいのデータ数ならそのままでも良いです。

(8)
確率を求める基本は樹形図です。

ここでは表で見ますが、
樹形図の方が早いですよ。
大きいさいころの目が
小さいさいころの目の\(\,2\,\)倍以上になるのは
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \,\color{blue}{4}\, & \,\color{blue}{5}\, & \,\color{blue}{6}\, \\ \hline
\,\color{red}{1}\, & & & & & & \\ \hline
\color{red}{2} & ○ & & & & & \\ \hline
\color{red}{3} & ○ & & & & & \\ \hline
\color{red}{4} & ○ & ○ & & & & \\ \hline
\color{red}{5} & ○ & ○ & & & & \\ \hline
\color{red}{6} & ○ & ○ & ○ & & & \\ \hline
\end{array}\)

\(\,36\,\)通り中\(\,9\,\)通りなので
　\(\hspace{4pt}\displaystyle \frac{9}{36}=\underline{　\frac{4}{9}　}\)

迷わず樹形図です。

(9)
１次関数の変化の割合は傾きと同じです。

関数\(\,y=ax^2\,\)における
\(\,x\,\)の値が\(\,1\,\)から\(\,4\,\)まで増加するときの
変化の割合は
　\(\hspace{4pt}(\,1\,,\,a\,)\)
　\(\hspace{4pt}(\,4\,,\,16\,a\,)\)
から
　\(\displaystyle \frac{16\,a-a}{4-1}=\color{red}{5\,a}\)
これと１次関数\(\,y=\color{red}{6}x+5\,\)と変化の割合が同じなので
　\(\begin{eqnarray}\displaystyle
5\,a&=&6\\
a&=&\underline{　\frac{6}{5}　}
\end{eqnarray}\)

関数に関係なく「変化の割合」は
　\(\displaystyle (変化の割合)= \frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}\)
です。

(10)
相似なので比例計算で求まります。

条件
　\(\,\mathrm{∠DBC=∠ACD}\,\)
　\(\,\mathrm{AB=6\,,\,AC=5}\,\)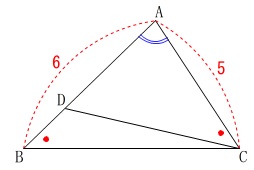共通の角があるので２角がそれぞれ等しいから
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△ACD}\,\)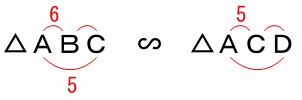よって
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AC}&=&\mathrm{AC:AD}\\
6:5&=&5:\mathrm{AD}\\
6\times \mathrm{AD}&=&25\\
\mathrm{AD}&=&\underline{　\frac{25}{6}　}(\mathrm{cm})
\end{eqnarray}\)

\(\,\large{1}\,\)は以上ですが
手を止めて考える問題はありません。

第２問

\(\,\large{2}\,\)
(1)から(3)までありますがそれぞれ別問題です。

(1)
座標上での四角形と三角形の面積比較です。

条件
　\(\,\mathrm{A\,,\,B}\,\)は関数\(\displaystyle \,y=\frac{5}{x}\,\)のグラフ上の点
　\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標はそれぞれ\(\,1\,,\,3\,\)
　\(\,\mathrm{AC\,,\,BD}\,\)は\(\,y\,\)軸と平行点\(\,\mathrm{A\,,\,B}\,\)の座標は
　\(\hspace{4pt}\mathrm{A}\,(\,1\,,\,5\,)\)
　\(\hspace{4pt}\displaystyle \mathrm{B}\,\left(\,3\,,\,\frac{5}{3}\,\right)\)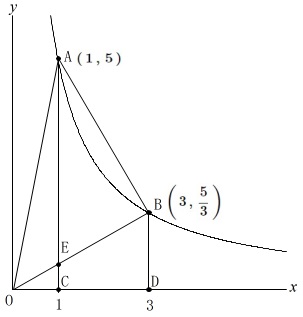ここまで手を止めるところはありません。

さて、
四角形\(\,\mathrm{ECDB}\,\)と\(\,\mathrm{△AOB}\,\)の面積です。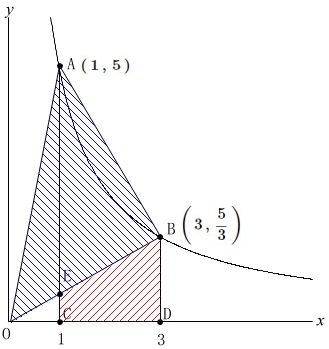比較するには基準になる部分が見つけにくいので
（ここで悩むより）
具体的な長さ、面積を求めた方が早いでしょう。

相似なので
　\(\,\mathrm{CE:DB=OC:OD=1:3}\,\)
であるから
　\(\hspace{4pt}\displaystyle \mathrm{DB}=\frac{5}{3}\,,\,\mathrm{CE}=\color{red}{\frac{5}{9}}\)
さらに
　\(\begin{eqnarray}\displaystyle \mathrm{AE}&=&\mathrm{AC-CE}\\
&=&5-\frac{5}{9}\\
&=&\color{blue}{\frac{40}{9}}
\end{eqnarray}\)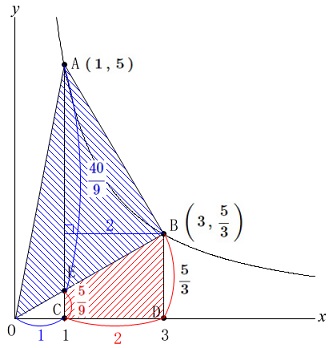なので
台形\(\,\mathrm{ECDB}\,\)の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
S_1&=&\left(\frac{5}{9}+\frac{5}{3}\right)\times \frac{2}{2}\\
&=&\frac{20}{9}
\end{eqnarray}\)
また\(\,\mathrm{△AOB}\,\)の面積\(\,S_2\,\)は
底辺を\(\,\mathrm{AC}\,\)とみて
　\(\begin{eqnarray}\displaystyle
S_2&=&\mathrm{△OAC+△BAC}\\
&=&\frac{1}{2}\times \frac{40}{9}\times (\color{blue}{1}+\color{red}{2})\\
&=&\frac{60}{9}
\end{eqnarray}\)

よって四角形\(\,\mathrm{ECDB}\,\)の面積は\(\,\mathrm{△AOB}\,\)の
　\(\hspace{10pt}\displaystyle \frac{20}{9}\div \frac{60}{9}\\
\displaystyle =\frac{20}{9}\times \frac{9}{60}=\underline{　\frac{1}{3}　}倍\)

2-(1)基準を作った別解１

反比例のグラフ上の点では軸で囲む長方形は常に一定になります。

⇒　比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方

このことを利用すると
　\(\,\mathrm{△OBD=△OAC}\,\)
であり共通の\(\,\mathrm{△OCE}\,\)をひくことで
　四角形\(\,\mathrm{ECDB}\,\)と\(\,\mathrm{△OAE}\,\)の面積は等しい
ことが分かります。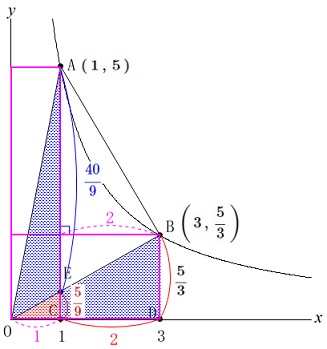また底辺\(\,\mathrm{AE}\,\)を等しくし高さが\(\,2\,\)倍なので
\(\,\mathrm{△ABE}\,\)の面積は\(\,\mathrm{△OAE}\,\)の\(\,2\,\)倍になります。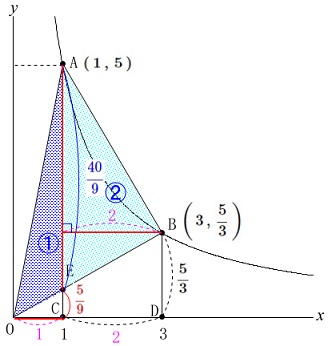よって
　\(\,\mathrm{△OAB}\,\)は四角形\(\,\mathrm{ECDB}\,\)の\(\,3\,\)倍
になります。

答え　\(\displaystyle \underline{　\frac{1}{3}　}倍\)　

2-(1)基準を作った別解２

\(\,\mathrm{△OCE}\,\)の面積を\(\,\color{magenta}{1}\,\)とすると
相似比（\(\,1:3\,\)）から面積比（\(\,1:9\,\)）を考えて
　四角形\(\,\mathrm{ECDB}\,\)の面積は\(\,\color{magenta}{8}\,\)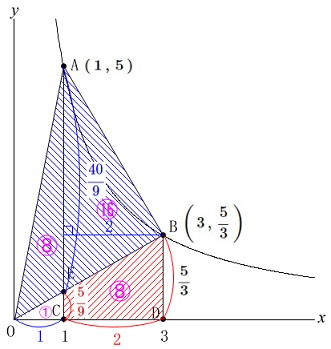高さ共通で
底辺となる\(\,\mathrm{AE}\,\)の長さは\(\,\mathrm{CE}\,\)の長さの\(\,8\,\)倍なので
　\(\,\mathrm{△OAE}=\color{magenta}{8}\,\)
（ここでも四角形\(\,\mathrm{ECDB}\,\)と\(\,\mathrm{△OAE}\,\)が等しいことが分かる。）
\(\,\mathrm{△ABE}\,\)は\(\,\mathrm{△OAE}\,\)と底辺\(\,\mathrm{AE}\,\)が同じで
高さが\(\,2\,\)倍なので
　\(\,\mathrm{△ABE}=\color{magenta}{16}\,\)
よって
　四角形\(\,\mathrm{ECDB}\,\)の面積は\(\,\color{magenta}{8}\,\)
　\(\,\mathrm{△OAB}\,\)の面積は\(\,\color{magenta}{8}+\color{magenta}{16}=\color{blue}{24}\,\)
だから
　\(\displaystyle \frac{\color{red}{8}}{\color{blue}{24}}=\underline{　\frac{1}{3}　}倍\)

具体的な面積計算が一番取り組みやすいかもしれません。
思い立った解法でどんどん進めて行かないと時間は多くありませんよ。

2-(1)別解（『覚え太郎』会員向け）

忘れてました。
『覚え太郎』『超え太郎』を見ている人向けの方法です。
（普通の中学生は見なくて良いですよ。）

少し計算過程を加えておきます。
　\(\begin{eqnarray}\displaystyle
\mathrm{△OAB}&=&\frac{1}{2}\times \left|1\times \frac{5}{3}-5\times 3\right|\\
&=&\frac{1}{2}\times \frac{40}{3}\\
&=&\frac{20}{3}
\end{eqnarray}\)
四角形\(\,\mathrm{ECDB}\,\)の面積\(\,S\,\)は
（\(\,\mathrm{CE}\,\)の長さを出していたとすると台形として）
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times \left(\frac{5}{3}+\frac{5}{9}\right)\times 2\\
&=&\frac{15+5}{9}\\
&=&\frac{20}{9}
\end{eqnarray}\)
または\(\,\mathrm{△OBD}\,\)の面積から相似比を利用して
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times \frac{5}{3}\times 3\times \frac{8}{9}\\
&=&\frac{20}{9}
\end{eqnarray}\)
　
よって
　\(\hspace{10pt}\displaystyle \frac{20}{9}\div \frac{20}{3}\\
\displaystyle =\frac{20}{9}\times \frac{3}{20}=\underline{　\frac{1}{3}　}倍\)

\(\,3\,\)点が分かる三角形があるので、
公式カード『覚え太郎』を見通している会員はおそらくこちらでしょう。

(2)
２つの連続する自然数の間にある分数の和です。

分母を５とする自然数は
　\(\displaystyle \frac{5}{5}\,,\,\frac{10}{5}\,,\,\frac{15}{5}\,,\cdots \,\frac{5n}{5}\)
となります。

１から２までの和は
　\(\displaystyle \frac{6+7+8+9}{5}=\frac{30}{5}=6\)
２から３までの和は
　\(\displaystyle \frac{11+12+13+14}{5}=\frac{50}{5}=\color{black}{\fbox{　10　}}\)
３から４までの和は
　\(\displaystyle \frac{16+17+18+19}{5}=\frac{70}{5}=\color{black}{\fbox{　14　}}\)
４から５までの和は
　\(\displaystyle \frac{21+22+23+24}{5}=\frac{90}{5}=\color{black}{\fbox{　18　}}\)

和だけを見ていくと
　\(\hspace{4pt}6\,,\,10\,,\,14\,,\,18\,,\cdots \)
と\(\,+4\,\)ずつ変化していくので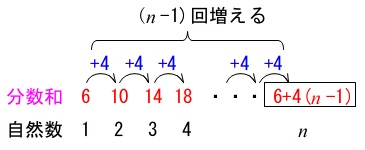\(\,1\,\)から\(\,n\,\)までは\(\,(n-1)\,\)回分\(\,+4\,\)増えるから
\(\,n\,\)から\(\,n+1\,\)までの間にある分数の和は
　\(\hspace{10pt}6+4(n-1)\\
=\underline{　4n+2　}\)

これは推測で出した答えでしかないのですが
\(\,\mathrm{\color{black}{\fbox{　Ⅰ　}}\,,\,\color{black}{\fbox{　Ⅱ　}}\,,\,\color{black}{\fbox{　Ⅲ　}}}\,\)とあるのでこれで良いでしょう。

　\(\displaystyle \,n=\frac{5n}{5}\,,\,n+1=\frac{5n+5}{5}\,\)
なので\(\,n\,\)から\(\,n+1\,\)までの間にある分数の和は

　\(\hspace{10pt}\displaystyle \frac{(5n+1)+(5n+2)+(5n+3)+(5n+4)}{5}\\
\displaystyle =\frac{20n+10}{5}\\
=\underline{　4n+2　}\)

一致しますので大丈夫です。

(3)
スマートフォンで動画を観ます。

充電しながらだと電池残量は増え、
充電せずに観ると電池残量は一定の割合で減ります。

ただ、増え方減り方の違いに注意が必要です。
充電しながらの場合
　\(\,4\,\)分で\(\,1\,\)％増える
ということは問題に書いてあります。

\(\,①\,\)
電池残量が\(\,25\,\)％から視聴をはじめます。
\(\,50\,\)分の動画を\(\,20\,\)分は充電しながら観て、
\(\,30\,\)分は充電無しで観て\(\,0\,\)％で終わった。

\(\,4\,\)分で\(\,1\,\)％増えるので\(\,20\,\)分では
　\(\hspace{4pt}\displaystyle \frac{20}{4}=5％\)
電池残量は増えています。
　\((\,20\,,\,30\,)\)

\(\,50\,\)分後に電池残量は\(\,0\,\)％なので
　\((\,50\,,\,0\,)\)

これらの座標を直線で結べば答えのグラフになります。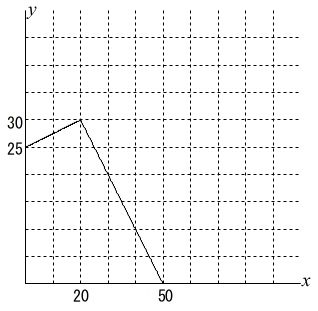
\(\,②\,\)
\(\,①\,\)から充電せずに動画を観ると
　\(\,1\,\)分間で\(\,1\,\)％電池残量は減る
ことが分かります。

\(\,x\,\)分間充電しながら観ると
　\(\displaystyle \frac{x}{4}（％）\)
電池残量は増えます。

残りを充電せずに観ると\(\,50-x\,\)分動画は残っているので
　\(\hspace{4pt}50-x　（％）\)
電池は減ります。

電池残量は\(\,0\,\)から始まり\(\,0\,\)以上で終われば
最後まで観ることができるので
　\(\begin{eqnarray}\displaystyle
\frac{x}{4}&≧&50-x\\
x&≧&200-4x\\
5x&≧&200\\
x&≧&40
\end{eqnarray}\)

答え　\(\,\underline{　40　分以上}\,\)

負の数をかけることもないので不等号の向きは変わりません。

第３問

(1)から(3)までつながりの無い別々の図形問題です。

(1)
「接線」と「接点と中心を結ぶ半径」とは垂直になります。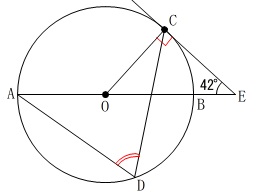直角三角形\(\,\mathrm{△OCE}\,\)の内角から
　\(\hspace{4pt}\,\mathrm{∠COE=48^{\circ}}\,\)
これから中心角となる
　\(\hspace{4pt}\mathrm{∠AOC}=132^{\circ}\)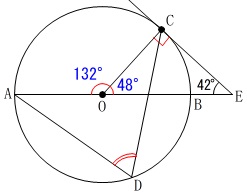
よってその円周角である\(\,\mathrm{∠CDA}\,\)は
　\(\hspace{10pt}\displaystyle \frac{132}{2}=\underline{　66　}度\)

(2)
条件は問題に目を通してください。
正方形と中点が３つあります。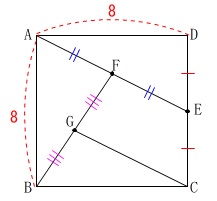
中点連結定理を利用するのでしょうが、
平行四辺形でないので面積が求めやすそうです。

\(\,①\,\)
線分\(\,\mathrm{GC}\,\)の長さを求めます。

正方形の中で考えると苦しくなります。
正方形が平行四辺形であることを思い出せば、
線分を延長しますが縦と横があるので解法は分かれるでしょう。

ここでは横に延長します。
（図の都合上ですので縦でも良いですよ。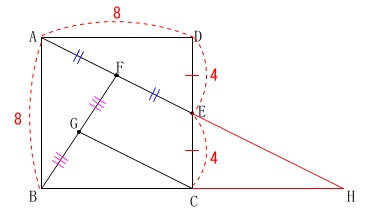）三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AE}&=&\sqrt{4^2+8^2}\\
&=&\sqrt{80}\\
&=&4\sqrt{5}
\end{eqnarray}\)
これから
　\(\hspace{4pt}\mathrm{FE}=2\sqrt{5}\)
　\(\hspace{4pt}\mathrm{EH}=4\sqrt{5}\)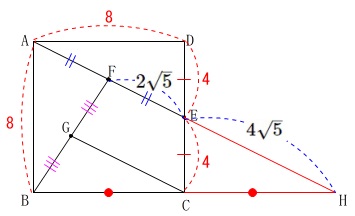
となるので
　\(\hspace{4pt}\mathrm{FH}=6\sqrt{5}\)
だから中点連結定理から\(\,\mathrm{FH}\,\)の半分で
　\(\hspace{10pt}\mathrm{GC}=\underline{　3\sqrt{5}　}\mathrm{cm}\)

※
縦に伸ばすのは\(\,\mathrm{DC}\,\)の延長に\(\,\mathrm{EC}\,\)と同じ長さの線分を加えます。

\(\,②\,\)
四角形\(\,\mathrm{FGCE}\,\)の面積を求めます。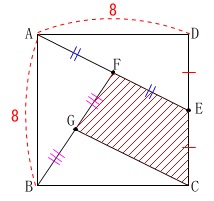
比を使うか、長さを使うかですが
どちらもそれほどややこしい計算はありません。

比を使う場合は\(\,①\,\)の図が利用できます。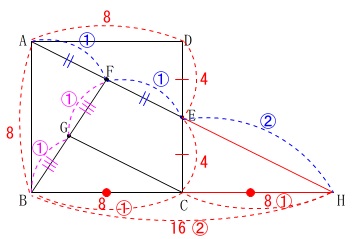正方形の面積は\(\,\mathrm{△ABH}\,\)と同じです。
　\(\hspace{4pt}\mathrm{△ABH}=64\)
部分的に三角形の面積を出していきましょう。
　\(\hspace{4pt}\displaystyle \mathrm{△ABF}=\frac{1}{4}\times \mathrm{△ABH}=\color{blue}{16}\)
これから
　\(\hspace{4pt}\displaystyle \mathrm{△BFH}=\mathrm{△ABH-△ABF}=48\)
相似比\(\,1:2\,\)で面積比が\(\,1:4\,\)なので
　\(\hspace{4pt}\displaystyle \mathrm{△BCG}=\frac{1}{4}\times \mathrm{△BFH}=\color{blue}{12}\)
また
　\(\hspace{4pt}\displaystyle \mathrm{△CEH}=\color{blue}{16}\)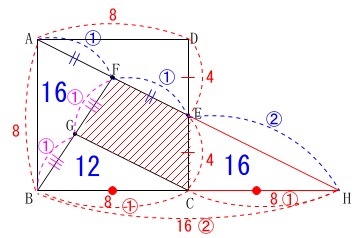
よって四角形\(\,\mathrm{FGCE}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&64-(16+12+16)\\
&=&\underline{　20　}\mathrm{cm^2}
\end{eqnarray}\)

長さを利用する場合は正方形で補助線を引きます。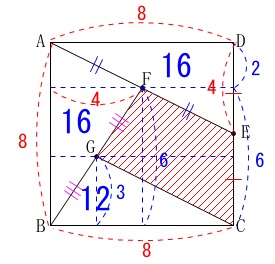
　\(\begin{eqnarray}\displaystyle
S&=&64-(16+16+12)\\
&=&\underline{　20　}　\mathrm{cm^2}
\end{eqnarray}\)

\(\,①\,\)でミスしても\(\,②\,\)に影響しませんね。

※注意
\(\,\mathrm{AE=BE}\,\)ですが、
\(\,\mathrm{AE⊥BF}\,\)ではありません。

(3)
正三角すいなので正三角形が２つあります。

条件
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DBC}\,\)は正三角形
　\(\mathrm{OA=OB=OC}=6\,,\,\mathrm{AB}=4\)正三角すいで長さが与えられているので
長さや体積はすべて計算できます。

ただ、\(\,②\,\)は比の値を求めるだけなのでその必要はありません。

\(\,①\,\)
線分\(\,\mathrm{DA}\,\)の長さを求めます。

線分\(\,\mathrm{DA}\,\)を含む面を抜き出しましょう。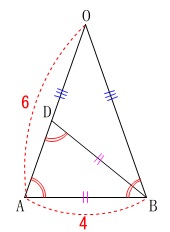二等辺三角形の底角が等しいので
　\(\,\mathrm{△OAB}\,\)　∽　\(\,\mathrm{△DBA}\,\)
であることが分かります。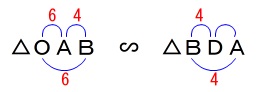
　\(\begin{eqnarray}\displaystyle
\mathrm{OA:BD}&=&\mathrm{AB:DA}\\
6:4&=&4:\mathrm{DA}\\
6\times \mathrm{DA}&=&16\\
\mathrm{DA}&=&\frac{16}{6}=\underline{　\frac{8}{3}　}\mathrm{cm}
\end{eqnarray}\)

\(\,②\,\)
立体\(\,\mathrm{ODBC}\,\)の体積と
正三角すい\(\,\mathrm{OABC}\,\)の体積の比の値を求めます。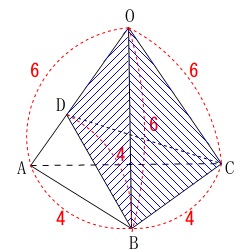具体的な体積を求めることもできますが、
\(\,\mathrm{①}\,\)で求めた線分の長さは高さの比を与えてくれるので
立体\(\,\mathrm{ODBC}\,\)の体積を\(\,V_1\,\)、
正三角すい\(\,\mathrm{OABC}\,\)の体積を\(\,V\,\)とすると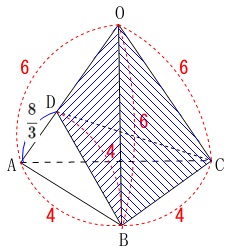
　\(\begin{eqnarray}\displaystyle
V_1:V&=&\left(6-\frac{8}{3}\right):6\\
&=&\frac{10}{3}:6\\
6\times V_1&=&\frac{10}{3}\times V\\
V_1&=&\frac{10}{3}\times \frac{1}{6}\times V\\
&=&\frac{5}{9}\times V
\end{eqnarray}\)

答え　\(\displaystyle \underline{　\frac{5}{9}　}倍\)

たぶん、説明が足りていないと思うので
体積を求める「つもり」で説明を加えておきます。

点\(\,\mathrm{O}\,\)と点\(\,\mathrm{D}\,\)から面\(\,\mathrm{ABC}\,\)に垂線を下ろすと
点\(\,\mathrm{A}\,\)から辺\(\,\mathrm{BC}\,\)に引いた中線上に下ります。分かり易くするために\(\,\mathrm{△OAM}\,\)を抜き出すと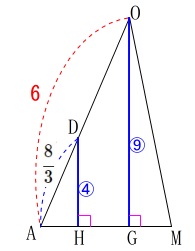
\(\begin{eqnarray}\displaystyle
\mathrm{DH:OG}&=&\frac{8}{3}:6\\
&=&4:9
\end{eqnarray}\)

※
\(\,\mathrm{△ABC}\,\)は正三角形なので中線\(\,\mathrm{AM}\,\)の長さは
　\(\hspace{4pt}\mathrm{AM}=2\sqrt{3}\)
点\(\,\mathrm{G}\,\)は\(\,\mathrm{△ABC}\,\)の重心になるので
　\(\hspace{4pt}\displaystyle \mathrm{AG}=\frac{4\sqrt{3}}{3}\)

これから高さも具体的な長さで出ますが、
比の解説なので比で進めます。

立体\(\,\mathrm{ODBC}\,\)の体積は
正三角すい\(\,\mathrm{OABC}\,\)から立体\(\,\mathrm{DABC}\,\)を引けば良い。

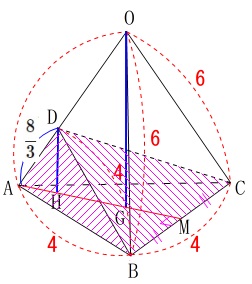
底面は同じ\(\,\mathrm{△ABC}\,\)で高さの比が
　\(\hspace{4pt}\mathrm{OG:DH}=9:4\)
なので立体\(\,\mathrm{DABC}\,\)の体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{DH}\\
&=&\color{red}{\frac{1}{3}\times \mathrm{△ABC}}\times \frac{4}{9}\times \color{red}{\mathrm{OG}}
\end{eqnarray}\)

正三角すい\(\,\mathrm{OABC}\,\)の体積\(\,V\,\)は
　\(\hspace{4pt}\displaystyle V=\color{red}{\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{OG}}\)
なので
　\(\hspace{4pt}\displaystyle V_2=\frac{4}{9}\times V\)

これから立体\(\,\mathrm{ODBC}\,\)の体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&V-V_2\\
&=&V-\frac{4}{9}\,V\\
&=&\left(1-\frac{4}{9}\right)\,V\\
&=&\frac{5}{9}\,V
\end{eqnarray}\)

この計算を線分の長さで分数のまま計算したのが上の解答です。

立体のまま高さの比較はしづらいでしょう？
面を抜き出すという基本作業は
確実にしておくことをお勧めして終わります。

以上です。

⇒　2021年（令和3年）度愛知県公立高校入試Ａの数学問題と解説

\(\,\mathrm{A}\,\)日程の解説はほとんどしておりません。
ここまでの解説の通りに\(\,\mathrm{A}\,\)日程の問題を解いてみてください。

作業手順が分かっているなら満点狙えるはずです。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

愛知県の公立入試数学は時間が厳しいですが、
基本、応用が全範囲でバランス良くできています。

過去問で対策にはなりませんが良い総復習になりますよ。