2018年(平成30年)度に神奈川県で行われた公立高校入試数学の問5の解説です。
確率の問題で文章が長いのでルールを読み取るのに時間が必要ですので時間配分を間違えないようにしたいところです。
確率の問題はルールがわからなければ始まらない
確率の問題も場合の数を求める問題も、ルールがわからなければ問題は解けません。
例えば、袋の中に\(\,2\,\)個の赤玉と\(\,1\,\)個の青色の玉が入っているとします。
何人かの人が順番にこの袋から玉を1個ずつとり出します。
誰かが青色の玉を引き出せば終わり、だとします。
このとき、\(\,1\,\)番目に引いた人が引いた玉を戻すのか戻さないかで終わる回数は変わってきます。
\(\,1\,\)番目の人が当たりを引く確率は
\(\,3\,\)個の中で\(\,1\,\)個が青玉なので \(\displaystyle \frac{1}{3}\) です。
このとき\(\,1\,\)回で終わる確率は \(\displaystyle \frac{1}{3}\) です。
戻さない場合は、\(\,1\,\)番目の人は赤玉を取り出しているので、
袋に残っている玉は、赤玉\(\,1\,\)個、青玉\(\,1\,\)個です。
だから\(\,2\,\)番目の人が青玉を取り出す確率は \(\displaystyle \frac{1}{2}\) です。
赤が\(\,2\,\)回続けて取り出されても\(\,3\,\)番目の人は必ず青玉を取り出すことになるので多くても\(\,3\,\)回しかありません。
しかし、\(\,1\,\)番目の人が玉を取り出して赤玉であったことを確認した後、玉を袋に戻すとすると、
\(\,2\,\)番目の人が青玉を取り出す確率は\(\,1\,\)番目の人と同じで \(\displaystyle \frac{1}{3}\) です。

\(\,3\,\)番目の人も同じ確率で、
(\(\,3\,\)番目の人が引いているとすれば\(\,1\,\),\(\,2\,\)番目の人は赤玉)
この場合はいつまでも終わらないこともあります。
このように確率では一つひとつの問題でルールが違うのです。
ルールを知らずにスポーツができないように、確率の問題もルールを知ることから始めます。
問5 確率問題のルールの確認
それではこの問題のルールを確認しておきましょう。
この問題は【ルール】と書いてくれているので確認しやすいです。
大きいさいころの目を \(a\)
小さいさいころの目を \(b\)
とします。
「二つのさいころを同時に\(\,1\,\)回投げ」は、\(\,1\,\)個ずつ投げても同じです。
【ルール①】
\(a\) と \(b\) の和だけ,点 \(\mathrm{A}\) を出発点とし,円の周上の点を時計回りに2つずつ移動させる。
これは簡単に言うと「2つのさいころの目の和だけ移動します」、ということです。
【ルール②】
\(a\) が \(b\) の約数であるとき,点 \(\mathrm{X}\) の次は円 \(\mathrm{O’}\)の周上の点を時計回りの順に移動させ,\(a\) が \(b\) の約数でないとき,点 \(\mathrm{X}\) の次は円 \(\mathrm{O}\) の周上の点を時計回りに順に移動させる。
これは \(a\) が \(b\) の約数なら1つ進んで点 \(\mathrm{X}\) についたら後は、円 \(\mathrm{O’}\) 上を時計回りにぐるぐる回り、
\(a\) が \(b\) の約数でないときは、移動なしで円 \(\mathrm{O}\) の周上をぐるぐる時計回りに変わるということです。
ややこしく見えますが二通りの回り方しかありません。
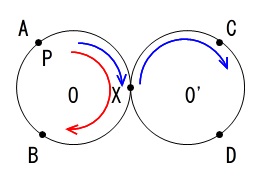
これがこの問題のルールです。
慣れてくるとこれがすぐに読み取れるのかというとそうではありません。
いくつかルールに従って試すのです。
ルールが理解できるまで何度も試すことで見えてきます。
確立はこれがすべて
問題には動き方の例が書かれているので、それで動き方を練習できます。
この練習をいくつすれば良いか?
36通りですべてです。
さいころの出目は大きいさいころが6つ、小さいさいころが6つの出目ありますが、
この2つの組み合わせは\(\,36\,\)通りしかありません。
これをすべて調べれば答えは必ずでます。
それを調べるには樹形図です。
\(\,36\,\)通りが多いか?
確かに高校入試では時間が短いかもしれませんが、\(\,36\,\)通りの樹形図を書くのにそれほど時間を必要とするでしょうか?
思っているほど時間はかかりません。
大学入試では樹形図が書き切れいないほどの場合がありますが、
高校入試では樹形図が書ききれるほどしか場合の数がないと考えていても良いくらい少ないです。
ただ、さいころ2つの場合は表が便利です。
赤い数字が大きいさいころの出目 \(\color{red}{a}\)
青い数字が小さいさいころの出目 \(\color{blue}{b}\)
中の数字は「和」 \(a+b\)
と見て下さい。
| 小\(\setminus\)大 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
同じ数字が斜めに並んでいることに気がつくでしょう。
この表を書くのは\(\,1\,\)分もかかりません。
確率の答えへの近道
試す数が多いほどルールの理解が深まります。
ルールがわからないまま考えてもなかなか答えは見つかりません。
\(\,36\,\)通り全部とはいいませんが、ルールがわかるまで試すと良いです。
試す数が多ければ多いほどルールが見えて、答えへの近道となります。
例えば、
\((\,a\,,\,b\,)=(\,1\,,\,1\,)\)
のときは \(a\) が \(b\) の約数なので円 \(\mathrm{O’}\) に移りながら2進みます。
\(\mathrm{A}\,\rightarrow\,\mathrm{X}\,\rightarrow\,\mathrm{C}\)
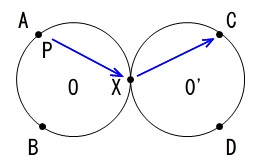
\((\,a\,,\,b\,)=(\,2\,,\,4\,)\)
のときは \(a\) が \(b\) の約数なので円 \(\mathrm{O’}\) に移りながら6進みます。
\(\mathrm{A}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{C}\,\rightarrow\,\mathrm{D}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{C}\,\rightarrow\,\mathrm{D}\)
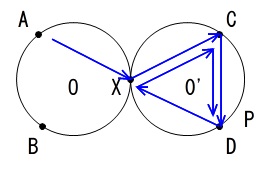
\((\,a\,,\,b\,)=(\,4\,,\,2\,)\)
のときは \(a\) が \(b\) の約数ではないので円 \(\mathrm{O}\) 上の点だけを移りながら6進みます。
\(\mathrm{A}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{B}\,\rightarrow\,\mathrm{A}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{B}\,\rightarrow\,\mathrm{A}\)
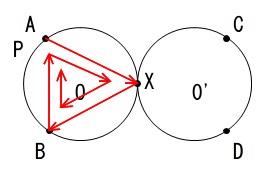
ここで「あれ?」と気がつきます。
もう一つ試してみます。
\((\,a\,,\,b\,)=(\,3\,,\,2\,)\)
のときは \(a\) が \(b\) の約数ではないので円 \(\mathrm{O}\) 上の点だけを移りながら5進みます。
\(\mathrm{A}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{B}\,\rightarrow\,\mathrm{A}\,\rightarrow\,\mathrm{\color{red}{X}}\,\rightarrow\,\mathrm{B}\)
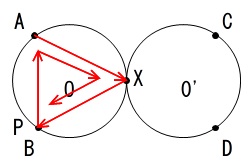
進み方は \(a\) が \(b\) の約数のときと約数でないときの二通りありますが、
どちらにも関係なくい移動回数\(\,1\,\)回目と\(\,4\,\)回目には必ず \(\color{red}{\mathrm{X}}\) にいます。
もっと試すと\(\,7\,\)回目も必ず \(\color{red}{\mathrm{X}}\) にいます。
ただし、\(a+b\) が\(\,1\,\)となることはありません。
ここまで気がつくと、
\(a\) が \(b\) の約数のときと約数でないとき
の二通りあるけど、進む数 \(a+b\) が決まれば
それぞれの円での位置は決まっているとわかります。
書いていけばわかるのでまとめて書いておきます。
\(a\) が \(b\) の約数のとき
(円 \(\mathrm{O’}\) 上を動きます。)
\(a+b\) が \(2,5,8,11\) のとき \(\mathrm{C}\)
\(a+b\) が \(3,6,9,12\) のとき \(\mathrm{D}\)
\(a+b\) が \(4,7,10\) のとき \(\mathrm{X}\)
\(a\) が \(b\) の約数でないとき
(円 \(\mathrm{O}\) 上を動きます。)
\(a+b\) が \(2,5,8,11\) のとき \(\mathrm{B}\)
\(a+b\) が \(3,6,9,12\) のとき \(\mathrm{A}\)
\(a+b\) が \(4,7,10\) のとき \(\mathrm{X}\)
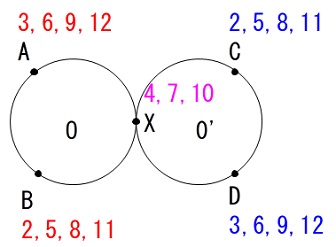
となっています。
これとさいころ2つ和を示した表を合わせると答えがすぐに出てきます。
問5の解き方と答えの出し方
(ア)
点 \(\mathrm{P}\) が点 \(\mathrm{X}\) にある確率です。
ルールを確認せずに考えると難しく思えるかもしれませんが、
書き出していくうちに、点 \(\mathrm{P}\) が \(\mathrm{X}\) にあるのは、
\(a\) が \(b\) の約数でも、約数でなくても関係なく
\(\color{magenta}{\,a\,+\,b\, が\, 4\,,\,7\,,\,10\, の場合}\)
だということがわかります。
| 小\(\setminus\)大 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ④ | 5 | 6 | ⑦ |
| 2 | 3 | ④ | 5 | 6 | ⑦ | 8 |
| 3 | ④ | 5 | 6 | ⑦ | 8 | 9 |
| 4 | 5 | 6 | ⑦ | 8 | 9 | ⑩ |
| 5 | 6 | ⑦ | 8 | 9 | ⑩ | 11 |
| 6 | ⑦ | 8 | 9 | ⑩ | 11 | 12 |
実際にはこの表は問題用紙か計算用紙に1つで良いですよ。
問題の違いによって○とか×とかで印を分けていけば良いのです。
時間はかからないので書き直した方が見やすいですけどね。
\(\,36\,\)通りの中で \(\mathrm{P}\) が \(\mathrm{X}\) の位置にあるのは○のついた\(\,12\,\)通りなので
求める確率は \(\displaystyle \frac{12}{36}=\underline{\frac{1}{3}}\)
樹形図でも同じ答えが出るはずなのでやってみると良いです。
さいころ2つの場合はこの表の方が楽だと気がつきます。
(イ)
点 \(\mathrm{P}\) が点 \(\mathrm{B}\) にある確率です。
点 \(\mathrm{B}\) の位置にある場合は \(a+b\) が \(2,5,8,11\) の場合ですが、
\(a\) が \(b\) の約数のときは、点 \(\mathrm{C}\) にあります。
だから、
\(a\) が \(b\) の約数ではなく、
\(a+b\) が \(2,5,8,11\)
の確率を出せば良いのです。
表から選んで見ましょう。
緑の数字が \(a+b\) が \(2,5,8,11\) の斜めの並びになりますが、
そのうち \(a\) が \(b\) の約数でないものは○がついた数字です。
| \(b\setminus a\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ⑤ | 6 | 7 |
| 2 | 3 | 4 | ⑤ | 6 | 7 | ⑧ |
| 3 | 4 | ⑤ | 6 | 7 | ⑧ | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | ⑧ | 9 | 10 | ⑪ |
| 6 | 7 | 8 | 9 | 10 | ⑪ | 12 |
調べるのは \(2,5,8,11\) の斜めの並びだけで良いのでたいした手間は必要ありません、
36通りのなかで\(\,8\,\)通りが点 \(\mathrm{P}\) が点 \(\mathrm{B}\) の位置にある場合になります。
とって求める確率は
\(\displaystyle \frac{8}{36}=\underline{\frac{2}{9}}\)
説明が長くて難しそうに見えますが、
やっていることは手を動かして、例を多く試しているだけですからね。
試験時間に実験をして規則性を見つけるというのは確率でも同じです。
文章が長いからルールの読み取りに時間がかかります。
他の問題をさっさと済ませて、確率の問題をじっくえり解けるようになれば満点目指せますよ。
高校受験の確率は樹形図ですべて解けるということは忘れないでください。
使い方によるのですべてというのは言い過ぎか?笑
似た問題は2018年だけでも全国の公立入試でたくさん出てましたよ。
⇒ 2018年度神奈川県公立高校入試の数学問6立体図形の考え方と解説
問6は立体です。空間図形でやることは決まってますよね。
立体が苦手という人は平面も苦手です。笑
