2018年(平成30年)度に神奈川県で行われた公立高校入試の問6にある立体問題の考え方と解説です。
3つの問題がありますが、2つは基本ですので公式と求め方を確認しておきましょう。
もう1つは応用ともいえますが割とよくでるタイプの問題です。
直通の方法もありますので手順さえ身についていれば答えはすぐに出ます。
⇒ 神奈川県2018数学問題
円錐の体積の公式を確認する問題
(ア)円錐の体積を求める問題です。
円錐に限らず、三角錐でも四角錐でも、
すべての錐体の体積は柱体の\(\,\displaystyle \frac{1}{3}\,\)
となります。
柱体の体積は
\(\color{magenta}{\fbox{(体積)=(底面積)×(高さ)}}\)
なので
\(\large{\color{red}{\fbox{(錐体の体積)=\(\,\displaystyle \frac{1}{3}\,\)×(底面積)×(高さ)}}}\)
これを忘れている受験生はほとんどいないでしょう。
後は確実に計算していくだけです。
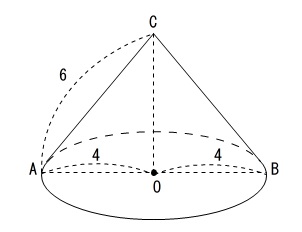
底面は円なので底面積は
半径4の円の面積
となります。
\(\,底面積=\pi \times (4)^2=16\,\pi\,\)
高さは頂点Cから底面に下ろした垂線\(\,\mathrm{\color{red}{OC}}\,\)の長さなので、
\(\,\triangle \mathrm{AOC}\,\)を抜き出して、
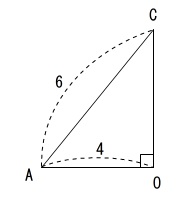
三平方の定理から
\(\begin{eqnarray}
\mathrm{OC}^2+4^2&=&6^2\\
\mathrm{OC}^2&=&36-16=20\\
\mathrm{OC}&=&\pm \sqrt{20}=\pm 2\sqrt{5}
\end{eqnarray}\)
\(\,\mathrm{OC}\,\)は長さなので\(\,\mathrm{OC}>0\,\)だから
\(\,\mathrm{OC}=2\sqrt{5}\,\)
よって求める円錐の体積は
\(\hspace{10pt}\displaystyle \frac{1}{3}\times 16\,\pi \times 2\sqrt{5}\\
\displaystyle =\underline{\frac{32\sqrt{5}}{3}}\)
錐体が柱体の\(\,\displaystyle \frac{1}{3}\,\)になるということを忘れていなければ、
高さを出すだけなので問題はないでしょう。
この問題では、母線がどこなのか書いてくれているので良いですが、
「母線って何?」という人がたまにいます。
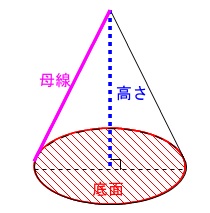
忘れないようにしておきましょう。
表面積を求めるときの合い言葉
(イ)は円錐の表面積を求めます。
『覚え太郎』を見ている人には当たり前のことなのですが、
こんな基本も未だに知らない中学生、高校生もいるので会員には耳にたこだろうけど説明をしておきます。
表面積という日本語を見たら展開図を書く
これは必ずやることです。
立体を立体のまま考えるなんてなかなかできません。
では手順通り展開図を書いていきましょう。
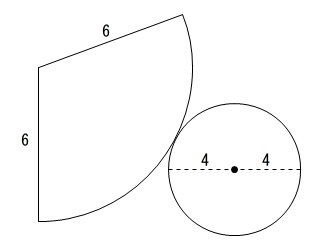
このような「感じ」です。
正確には扇形の中心角が違いますが最初からわかっているわけではありません。
(中心角が違うからといって書き直す必要もありません。)
ここでポイントになるのが中心角がわかっていないということです。
実は面積を出すだけなら中心角は必要ないのですが、
中心角も出せないなんて受験生としては足りていないので比例式を利用して求めておきましょう。
展開図で底面の円周と扇形の弧が等しいというのが注目点です。
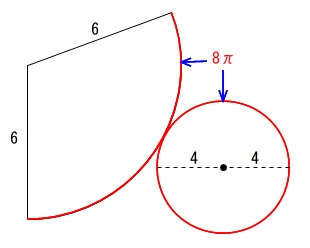
半径4の円周は \(2\,\pi \times 4=8\,\pi\)
なので扇形の弧の長さも\(\,8\,\pi\,\)です。
ここで扇形の半径は\(\,6\,\)なので中心角が\(\,360^{\circ}\,\)となる場合
円周の長さは \(\,2\,\pi \times 6=12\,\pi\,\)
ところが弧の長さは \(\,8\,\pi\,\) なので中心角を\(\,x^{\circ}\,\)とすると
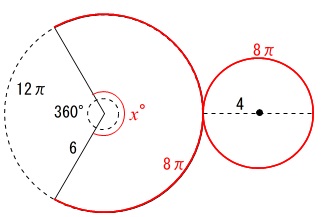
\(\,12\,\pi\,\,\)のときに\(\,360^{\circ}\,\)
\(\,8\,\pi\,\)のときは\(\,x^{\circ}\,\)
を比例式にして(\(\,^{\circ}\,\)は書かなくて良いです。)
\(\,12\pi:8\pi=360:x\,\)
これから
\(\begin{eqnarray}
12\pi x&=&8\pi \times 360\\
\displaystyle x&=&\frac{8\pi}{12\pi}\times 360\\
&=&240
\end{eqnarray}\)
扇形の中心角は \(\,240\,^{\circ}\,\)
半径\(\,6\,\)の円の面積は \(\pi\,(6)^2=36\pi\)
なので扇形の面積も比例式で出せます。
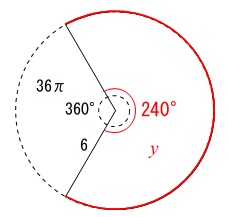
扇形の面積を\(\,y\,\)とすると、
\(\,360^{\circ}\,\)のときに\(\,36\,\pi\,\,\)
\(\,240\,^{\circ}\,\)のときは\(\,y\,\)
なので
\(360:240=36\pi:y\)
これから
\(\begin{eqnarray}
360y&=&240\times 36\pi\\
\displaystyle y&=&\frac{240\times 36\pi}{360}\\
y&=&24\pi
\end{eqnarray}\)
これは公式としてあつかう場合が多いのではないでしょうか。
扇形の半径を\(\,r\,\)、中心角を\(\,a^{\circ}\,\)とすると
\(\displaystyle \,\color{red}{扇形の面積=\pi \times r^2 \times \frac{a}{360}}\,\)
だから
\(\displaystyle y=\pi\times (6)^2\times \frac{240}{360}\\
\displaystyle =36\pi \times \frac{2}{3}\\
=24\pi\)
ただ、これを意味なく覚えても使えない中学生が多いので、公式推進派の私ですがおすすめしておりません。笑
この基本になる比例関係が分ければ弧も面積も出せるので、比例式を立てる方を優先します。
ただ、この比例式が使えるようになった後で覚えるなら便利な公式もあります。
弧の長さが\(\,\ell\,\)で半径が\(\,r\,\)の扇形の面積は
\(\displaystyle \,\color{red}{S=\frac{1}{2}\,\ell \,r}\,\)
弧の長さを底辺、半径を高さとする三角形と同じ公式です。
扇形の弧の長さが\(\,8\pi\,\)とわかった時点で面積は
\(\,\displaystyle \frac{1}{2}\times 8\pi \times 6=24\pi\,\)
と出せますし、
円錐の底面の半径\(\,4\,\)、母線\(\,6\,\)となっている時点で
扇形の面積は
\(\,\displaystyle \pi \times 6 \times 4=24\pi\,\)
と求まりますし、
何も図示しなくても表面積は
\(\pi \times 4 \times (4+6)=40\pi\)
と直接求めることもできます。
表面積とあれば展開図を書く
という定石を知ってれば必要ないのでここでは公式の説明はしません。
比例式利用での表面積をまだ出していませんでした。
扇形の面積は求まりました。\(\,24\pi\,\)です。
底面の面積は半径\(\,4\,\)の円なので、
\(\,\pi \times (4)^2=16\pi\,\)
これと扇形の面積を足すことで表面積が求まります。
\(24\pi+16\pi=\underline{40\pi}\)
たかが表面積に説明が長すぎましたが、苦手な人はここまででいいです。
配点は(ア)(イ)で10点分あります。
次はちょっとした応用とずるい公式があります。
立体図形の問題を解くときの基本的なこと
(ウ)円錐の中を抜けている線分の長さです。
円錐の周りを回って最短距離、という問題も多いですが、こちらは立体的に見なくてはならないような気がする問題です。
ここで立体問題の基本的な考え方をお伝えします。
今までの解説でもわかってきているかもしれませんが、立体をあつかう問題では立体で考えないというのがポイントになります。
立体の問題なのですが、立体のまま考えない、ということです。
慣れれば立体のままでもイメージできるようになりますが、
\(\color{red}{\fbox{平面を抜き出して考える}}\)
というのが、私のような凡人には向いています。笑
高校の数学で空間図形を見るときも同じです。
天才のマネができれば良いですが、普通に問題は解けるので平面で考えれば良いです。
この問題では、点\(\,\mathrm{E}\,\)は\(\,\triangle \mathrm{ACD}\,\)上にあるので、
\(\,\triangle \mathrm{ACD}\,\)を抜き出せば良いのです。
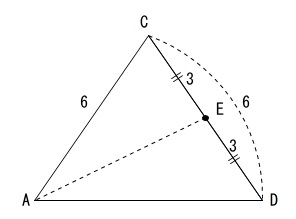
求めるのは線分\(\,\mathrm{AE}\,\)ですが、\(\,\mathrm{AD}\,\)の長さがわからなければ求まりません。
そこで今度は\(\,\mathrm{AD}\,\)を含む平面を考えます。
底面の中にある\(\,\triangle \mathrm{OAD}\,\)を抜き出します。
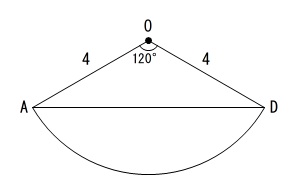
これから\(\,\mathrm{AD}\,\)を直接求めるには高校の定理が必要になるので、中学生は垂線を引いて三平方の定理を利用します。
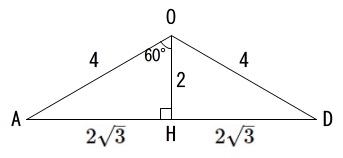
\(\,\mathrm{O}\,\)から\(\,\mathrm{AD}\,\)に垂線\(\,\mathrm{OH}\,\)を引くと三角定規の辺の比が利用できます。
\(\mathrm{OH:OA:AH}=1:2:\sqrt{3}\)
で\(\,\mathrm{OA}=4\,\)なので
\(\mathrm{OA:AH}=4:2\sqrt{3}\)
よって
\(\,\mathrm{AD}=2\mathrm{AH}=4\sqrt{3}\,\)
これを書き込めていなかったので図に書き込みます。
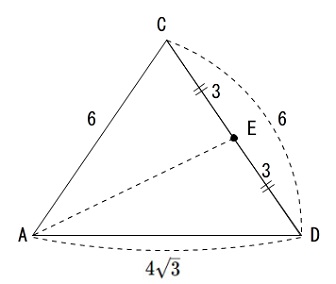
ここまで書き込めても中学生には簡単に答えの出る問題ではありません。
角の二等分線なら簡単に答えが出てきますが、\(\,\mathrm{AE}\,\)は角の二等分線ではなく中線です。
中線と角の二等分線を間違える場合が多いので気をつけてくださいね。
中線の場合は定理があるにはあるのですが、中学生では教科書にありません。
なのでちょっと面積の応用をします。
三角形は回転しても面積は変わりませんよね?
そのことを利用して底辺と高さの組を変えて等式にします。
この問題に合わせて説明しますが、よく使われる手法ですので覚えておくと良いです。
\(\triangle \mathrm{ACD}\) の面積を二通りの方法で表してみましょう。
頂点\(\,\mathrm{C}\,\)から\(\,\mathrm{AD}\,\)に垂線\(\,\mathrm{CF}\,\)を引くと
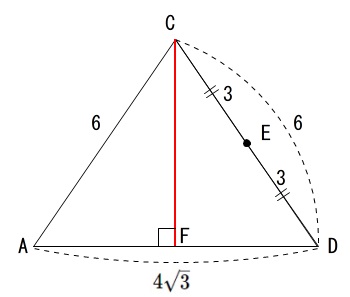
底辺を\(\,\mathrm{AD}\,\)として高さを\(\,\mathrm{CF}\,\)とする三角形の面積として
\(\begin{eqnarray}
\displaystyle \color{red}{\triangle \mathrm{ACD}}&=&\frac{1}{2}\times \mathrm{AD} \times \mathrm{CF}\\
\displaystyle &=&\frac{1}{2}\times 4\sqrt{3}\times \mathrm{\color{magenta}{CF}}
\end{eqnarray}\)
ここで\(\,\mathrm{CF}\,\)は二等辺三角形の頂角の二等分線なので、
底辺を垂直に二等分するから(二等辺三角形の定理)
\(\,\mathrm{AF=DF=2\sqrt{3}}\,\)

三平方の定理から
\(\begin{eqnarray}
\mathrm{AF^2+CF^2}&=&\mathrm{AC^2}\\
\mathrm{(2\sqrt{3})^2+CF^2}&=&(6)^2\\
\mathrm{12+CF^2}&=&36\\
\mathrm{CF^2}&=&36-12=24\\
\mathrm{CF}&=&\pm \sqrt{24}\\
&=&\pm 2\sqrt{6}
\end{eqnarray}\)
\(\,\mathrm{CF}\,\)は長さを表すから\(\,\mathrm{CF>0}\,\)なので
\(\,\mathrm{\color{magenta}{CF}}=2\sqrt{6}\,\)
これで面積が求めることができます。
\(\begin{eqnarray}
\displaystyle \triangle \mathrm{ACD}&=&\frac{1}{2}\times \mathrm{AD \times CF}\\
&=&\frac{1}{2}\times 4\sqrt{3}\times 2\sqrt{6}\\
&=&4\sqrt{18}=\color{red}{12\sqrt{2}}
\end{eqnarray}\)
もう一つ別の方向から見ます。
頂点 \(\,\mathrm{A}\,\) から \(\,\mathrm{DC}\,\) 垂線 \(\,\mathrm{AG}\,\) を引くと
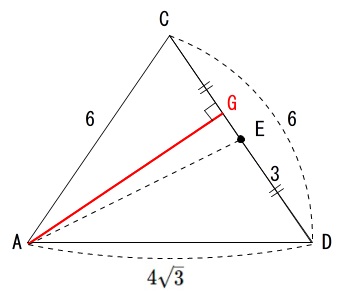
(\(\,\mathrm{E}\,\)は\(\,\mathrm{DC}\,\)の中点ですが\(\,\mathrm{G}\,\)は中点とはなりません。)
底辺を\(\,\mathrm{DC}\,\)として高さを\(\,\mathrm{AG}\,\)とする三角形の面積として
\(\begin{eqnarray}
\displaystyle \mathrm{\triangle ACD}&=&\mathrm{\frac{1}{2}\times DC \times AG}\\
\displaystyle &=&\frac{1}{2}\times 6 \times \mathrm{\color{magenta}{AG}}\\
&=&3\mathrm{\color{magenta}{AG}}
\end{eqnarray}\)
と表せます。
これは先ほど求めた\(\,\mathrm{\triangle ACD}\,\)の面積と等しいので、
\(\begin{eqnarray}
3\mathrm{\color{magenta}{AG}}&=&12\sqrt{2}\\
\mathrm{\color{magenta}{AG}}&=&\frac{12\sqrt{2}}{3}\\
&=&4\sqrt{2}
\end{eqnarray}\)
この回転や移動をしても、高さと底辺を変えてみても、
1つの図形の面積は等しい(変化しない)ことを利用するのは大学入試でもよく使いますので覚えておきましょう。
まだですよ。笑
求めたいのは\(\,\mathrm{AE}\,\)です。
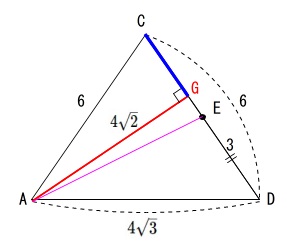
ここまできても\(\,\mathrm{AE}\,\)の長さはわからないでしょう。
わかる長さから求めていきましょう。
\(\triangle \mathrm{ACG}\)は直角三角形なので三平方の定理が使えます。
\(\begin{eqnarray}
\mathrm{AG^2+CG^2}&=&\mathrm{AC^2}\\
\mathrm{CG^2}&=&\mathrm{AC^2-AG^2}\\
&=&6^2-(4\sqrt{2})^2\\
&=&36-32=4
\end{eqnarray}\)
\(\mathrm{CG}>0\)なので
\(\mathrm{\color{magenta}{CG}=2}\)
ようやく答えに向かえます。
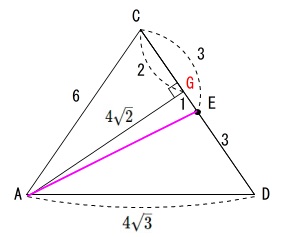
\(\,\mathrm{E}\,\)は\(\,\mathrm{DC}\,\)の中点だったので\(\,\mathrm{\color{red}{CE}=3}\,\)なので
\(\,\mathrm{EG=\color{red}{CE}-\color{magenta}{CG}}=3-2=1\,\)
最後です。
\(\triangle \mathrm{AEG}\)は直角三角形なので三平方の定理より
\(\begin{eqnarray}
\mathrm{AE^2}&=&\mathrm{AG^2+EG^2}\\
&=&(4\sqrt{2})^2+1^2\\
&=&32+1=33
\end{eqnarray}\)
\(\mathrm{AE}>0\)なので
\(\mathrm{AE}=\underline{\sqrt{33}}\)
ものすごく遠回りに思えますが、図を見ながら求められる長さを順に出していけば試験場ではこうなるのではないでしょうか。
もちろん途中の考え方を詳しく書く必要はありませんので、計算はそれほどきついものではないからそれほど時間はかかりません。
ここからは会員向け『超え太郎』マスターへの説明です。
一般の高校受験生は見なくても良いです。
まずは面積の等しいことを利用する方法を覚えておきましょう。
\(\,\mathrm{AD}\,\)の長さが求まった時点で、
\(\begin{eqnarray}
\mathrm{\color{red}{2(AE^2+DE^2)}}&=&\mathrm{\color{red}{AC^2+AD^2}}\\ \\
\mathrm{2AE^2+2(3)^2}&=&\mathrm{6^2+(4\sqrt{3})^2}\\
\mathrm{2AE^2+18}&=&\mathrm{36+48}\\
\mathrm{2AE^2}&=&36+48-18=66\\
\mathrm{AE^2}&=&33
\end{eqnarray}\)
\(∴ \mathrm{AE}=\underline{\sqrt{33}}\)
\(\large{\color{red}{\fbox{\(\,\mathrm{\color{red}{2(AE^2+DE^2)}}=\mathrm{\color{red}{AC^2+AD^2}}\,\)}}}\)
は中線定理です。
(『超え太郎』三平方の定理Q66 )
途中の計算は移項してからでもどうでも良いので確実に進めてください。
この問題では答えだけなので定理の説明も必要ないでしょう。
(ウ)も5点です。
数学での高得点が必要な人はやることやってしっかり得点しましょう。
やっていることは基本定理の繰り返しです。
⇒ 神奈川県公立高校入試2018の数学問7(平面図形)の解説
問7は時間をかけたくない平面図形問題です。
問4からは問6までは問題の意味を読み取るのに時間が必要です。
⇒ 神奈川県公立高校入試問題(平成30年度)の数学の過去問解説(公開)
まででを素早く確実にとっておくようにすると良いですね。
