Warning: Undefined array key "file" in /home/kashiwada/fromhimuka.com/public_html/math/wp-includes/media.php on line 1788
神奈川公立高校入試2018年(平成30年度)の数学問4の解説です。
問4は関数と図形が融合された総合問題です。
基本作業を続けていけば難しい問題ではありませんが、作業量に見合わない配点があります。笑
2018 神奈川県公立高校入試の問4関数総合問題
神奈川県に限らず、関数でやることは決まっています。
最後の(ウ)、面積比の問題は会員向けに書いた場合は割と楽だったのですが、
一般公開となると中学生の教科書の範囲での説明になるので私自身がめんどくさかった。笑
解法は過去問題集や他の塾の方がきれいだと思います(見てないので知りませんがwww)ので、きれいな解法を求めている人は他を参考にしてください。
比例定数を求める方法
(ア)
曲線② \(y=ax^2\) は原点を通る2次関数で、
\(y\,は\,x^2\,に比例する\)
といい、わかっているとは思いますが、\(a\) は比例定数といいます。
比例や反比例のときも比例定数なので覚えておきましょう。
比例定数は曲線上の原点以外の1点がわかれば良いので、それを探しにいきます。
ちなみにですが、数学で曲線というのは直線を含みますからね。
中学校の先生には間違えている人もいらっしゃるのであなただけは気をつけておいて下さい。
ただ、関数の問題でいきなり問に入るというのは、問題を難しくする原因です。
関数に限ったことではありませんけど、条件やルールの確認はある程度してから問に入るとさらっと終わったりもしますよ。
条件をできるだけ出しておくことがポイントになりますが、
問題文に書いてある順番に書き出してみましょう。
直線①は \(y=x+6\)
曲線②は \(y=ax^2\)
点Aの \(x\) 座標は \(x=-3\)
点Bの \(x\) 座標は \(x=6\)
\(\mathrm{CO:OD}=6:7\) で点Dの \(y\) 座標は負
\(\mathrm{AE=ED}\)
直線BFは \(y\) 軸に平行
と書いてあります。
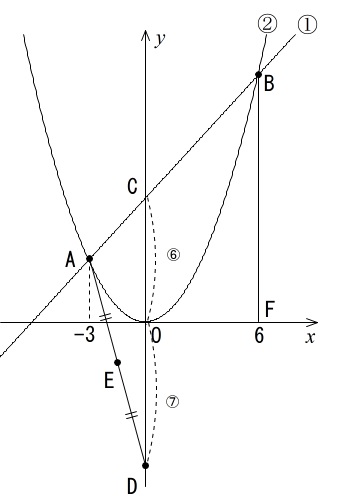
これをもっと具体的にしましょう。
点 A は直線 \(y=x+6\) 上の点なの \(x=-3\) を代入して
\(y=(-3)+6=3\)
となるので点 A の座標がわかります。
\(\color{red}{\mathrm{A}\,(\,-3\,,\,3\,)}\)
点 B も直線 \(y=x+6\) 上の点なの \(x=6\) を代入して
\(y=(6)+6=12\)
となるので点 B の座標もわかります。
\(\color{red}{\mathrm{B}\,(\,6\,,\,12\,)}\)
また D は \(y\) 軸上で \(\mathrm{CO:OD}=6:7\) の負の位置にあるので、
\(\color{red}{\mathrm{D}\,(\,0\,,\,-7\,)}\)
F は B から \(x\) 軸に垂線を下ろした点なので
\(\color{red}{\mathrm{F}\,(\,6\,,\,0\,)}\)
さらに点 E は AD の中点なので、
\(\mathrm{A}\,(\,-3\,,\,3\,)\) \(\mathrm{D}\,(\,0\,,\,-7\,)\)
から
\(\displaystyle \left(\,\frac{-3+0}{2}\,,\,\frac{3+(-7)}{2}\,\right)=\left(\,-\frac{3}{2}\,,\,-2\,\right)\)
なので
\(\displaystyle \color{red}{\mathrm{E}\,\left(\,-\frac{3}{2}\,,\,-2\,\right)}\)
点Cは① \(y=x+6\) の切片( \(y\) 切片)なので
\(\color{red}{\mathrm{C}\,(\,0\,,\,6\,)}\)
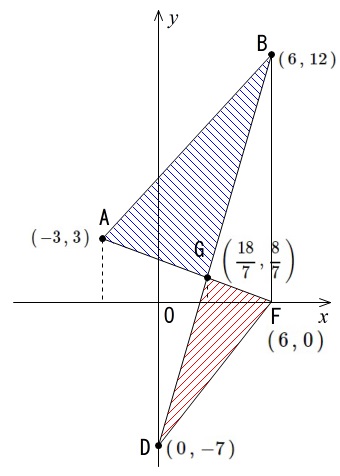
ここまでを書き込むと
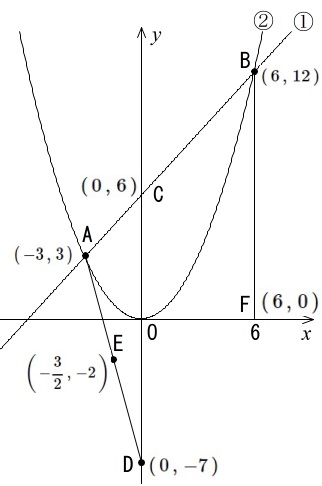
説明が長いからややこしそうに見えるけど、自分でやってみたらわかります。
すぐに終わるから。
やってみないとわからないし、これを出さないと問には答えられません。
これでかなりのことがわかります。
普通の問題なら半分以上答えが出せるはずです。
点Aと点Bは直線①上の点ですが、曲線②上の点でもあります。
交点とはそういう(両方の曲線上にある)点のことですから、覚えておきましょう。
どちらでも良いですが、1点を②に代入して比例定数を決めましょう。
どっちでも良いのですが、点A \((\,-3\,,\,3\,) \)を代入してみます。
\(3=a\times (-3)^2=9a\) から \(\displaystyle \underline{a=\frac{1}{3}}\)
当然点B \((\,6\,,\,12\,) \)を代入しても
\(12=a\times (6)^2=36a\) から \(\displaystyle \underline{a=\frac{1}{3}}\)
同じにならないとおかしい。
(ア)は \(\displaystyle \underline{a=\frac{1}{3}}\)
1次関数は異なる2点があれば求まる
(イ)は
「 2点 E , F を通る 1 次関数 \(y=mx+n\) を求めよ。」
と同じです。
ただ、答えを選ぶ形で出題されているだけです。
こんな問題は 1 次関数の決定問題で教科書でもたくさんやっているでしょう。
図に書き込んだ座標を抜き出せば簡単です。

※
ここでは縦に説明が長いので図が遠いように感じますが、
実際の試験では自分で書き込んだ図は目の前にあるのです。
つまりは \(2\) 点
\(\displaystyle \mathrm{E}\,\left(\,-\frac{3}{2}\,,\,-2\,\right)\) \(\mathrm{F}\,(\,6\,,\,0\,)\)
を通る直線の式を求めることになります。
1次関数の求め方は、
\(\color{black}{\fbox{連立方程式を解く}}\)
\(\large{\color{red}{\fbox{傾きを求めて、切片を求める}}}\)
の二つに大きくわけられます。
慣れている方で良いですが、傾きから求める方を勧めます。
問題によってはたくさんの直線を求めなければなりません。
連立方程式を何度も解くのはいやです。笑
その他にも理由はありますが、強制はしないことにします。
説明するのも、会員にしたら聞くのもいやになっているだろうけど、しつこくします。笑
それだけ大切なんですよ。
\(\displaystyle \color{red}{傾き=変化の割合=\frac{\hspace{4pt} y\,の増分\hspace{4pt}\, }{\hspace{4pt}xの増分\hspace{4pt}\, }}\)
「変化の割合」はすべての関数に使う言葉なので覚えておきましょう。
1次関数では傾きに一致するだけですよ。
傾きを出すときは座標二つを縦に並べて、同じ方向に引いて増分を出します。
\(x\,の増分\)で下から上を引いたら、\(y\,の増分\)も下から上を引きます。
一方を逆にすると符号が変わりますから気をつけておきましょう。
下から上を引くと決めておけば良いだけです。
\(\displaystyle \mathrm{E}\,\left(\,-\frac{3}{2}\,,\,-2\,\right)\)
\(\mathrm{F}\hspace{4pt}(\hspace{10pt}6\,\hspace{4pt},\hspace{6pt}0\hspace{4pt})\)
なので
\(\displaystyle \,x\,の増分=6-\left(-\frac{3}{2}\right)=\frac{12+3}{2}=\color{red}{\frac{15}{2}}\)
\(\,y\,の増分=0-(-2)=0+2=\color{blue}{2}\)
だから \(y=mx+n\) の傾き(変化の割合)\(m\) は
\(\displaystyle m=\frac{\color{blue}{2}}{\color{red}{\frac{15}{2}}}=\color{blue}{2}\times \color{red}{\frac{2}{15}}=\underline{\frac{4}{15}}\)
割り算は逆数のかけ算になるのは説明はいらないですよね。
\(m\) が決まったので \(y=mx+n\) に戻します。
\(\displaystyle y=\frac{4}{15}x+n\)
この直線は2点 \(\mathrm{E},\mathrm{F}\) を通るのでどちらかを代入すれば \(n\) が求まります。
\(\mathrm{F}\,(\,6\,,\,0\,)\) を代入すると
\(\displaystyle 0=\color{red}{\frac{4}{15}\times (6)}+n=\color{red}{\frac{8}{5}}+n\)
なので、
\(\displaystyle n=\underline{-\frac{8}{5}}\)
もちろん点 \(\displaystyle \mathrm{E}\,\left(\,-\frac{3}{2}\,,\,-2\,\right)\) を代入しても同じです。
\(\displaystyle -2=\color{magenta}{\frac{4}{15}\times \left(-\frac{3}{2}\right)}+n=\color{magenta}{-\frac{2}{5}}+n\)
から
\(\displaystyle n=-2+\frac{2}{5}=\frac{-10+2}{5}=\underline{-\frac{8}{5}}\)
ここでも言っておきましょうか。
分数計算は分母を1つにして、分子の計算に集中した方がミスは減りますよ。
連立方程式でも解いておきましょうか。
\(y=mx+n\) が \(2\) 点
\(\displaystyle \mathrm{E}\,\left(\,-\frac{3}{2}\,,\,-2\,\right)\) \(\mathrm{F}\,(\,6\,,\,0\,)\)
を通るので、
\( \begin{cases}
\hspace{6pt} \displaystyle -2=-\frac{3}{2}m+n\\
\hspace{12pt} 0=6m+n
\end{cases}\)
分母の残った形は気持ち悪いので、
上の方程式を両辺2倍しておきます。
\( \begin{cases}
\hspace{6pt} -4=-3m+2n\\
\hspace{12pt} 0=6m+n
\end{cases}\)
加減法でも代入法でも良いですが、下の式から
\(n=-6m\) として上の方程式に代入してみましょう。
\(\begin{eqnarray}
-4&=&-3m+2(-6m)\\
-4&=&-3m-12m\\
-4&=&-15m
\end{eqnarray}\)
これから \(\displaystyle m=\frac{4}{15}\)
これを上の連立方程式で出てきたどれかに代入すれば \(n\) が求まります。
変形済みの \(n=-6m\) に代入しましょう。
\(\displaystyle n=-6\times \frac{4}{15}=-\frac{8}{5}\)
簡単です。
でも後でやりますが(ウ)のような問題でこれを繰り返すって、私ならお断りします。
つまり、直線を求めるときは連立方程式は使いたくは無いと言うことです。笑
使って良いですよ。
答えが出れば間違いなく正解で点数はもらえます。
ただ、私はお断りするというだけです。
連立方程式を解くのは、交点を求めるときだけでおなかいっぱいになりますからね。
関数と面積比の応用問題の解き方
(ウ)
問4の続き問題ですが、条件が加わりますので図への書き込みが必要です。
この問題を解こうとするレベルにあれば図に書き込まないということはないとは思いますが、
図を書いて必要な情報を抜き出さない限りこの手の関数問題は解けません。
逆に、ここでやることすべてを習得できればほとんどの関数問題はクリアーできるようになります。
会員向けのままだと一般の受験生には理解できない部分が出てくると思うので、
教科書の範囲内での説明を加えておきますので長くなると思いますが参考にして下さい。
追加条件は
\(\color{red}{\mathrm{AF} と \mathrm{BD} の交点を \mathrm{G}}\)
だけですが、求めるものが少しややこしい位置にあります。
気がつけば楽、気がつかなければ捨てる?
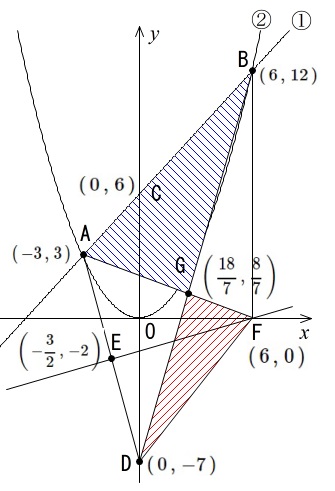
先ず書き込んだ図を見ておきましょう。
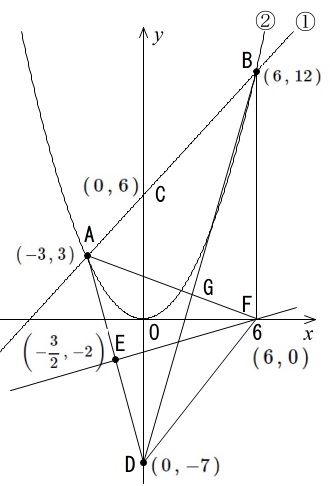
そういえばまだ直線 EF を書き込んでなかったですね。
問題の図に座標を入れるとこうなります。
問題は
\(\color{red}{三角形 \mathrm{AGB} と三角形 \mathrm{DFG} の面積比}\)
を聞いています。
図のどこかは確認しておきましょう。
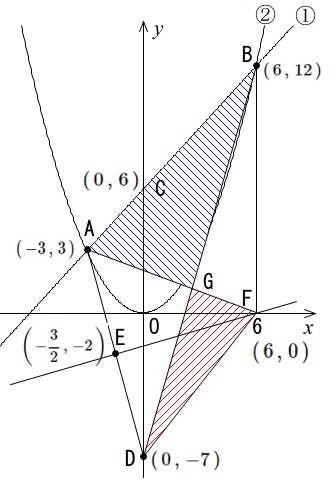
さて、早速ですが関数の問題では
\(\color{magenta}{\fbox{すべての交点}}\)
\(\color{red}{\fbox{すべての直線}}\)
が求まればほぼ解けます。
これが誘導から省かれる部分で、差がつくポイントなのです。
ただ、すべてを求めていたら時間がかかるので、そこが考えどころですね。
ここでは、すべての直線を出しておきます。
交点は連立すれば出るので後にします
解法は中学生向けに後でまとめます。
線分で書いているものも含め直線は6本です。
\(\mathrm{AB\,,\,\color{red}{AF}\,,\,\color{green}{AD}\,,\,EF\,,\,\color{magenta}{BD}\,,\,\color{orange}{DF}}\)
軸や定直線 \(\mathrm{BF}\,(x=6)\) は省いていますので1次関数は6本としておきましょう。
\(\mathrm{AB}\,:\,y=x+6\)
\(\displaystyle \mathrm{EF}\,:\,y=\frac{4}{15}x-\frac{8}{5}\)
はわかっています。
求め方は先ほど(イ)で説明したので省きます。
直線 \(\mathrm{\color{red}{AF}}\) は \((\,-3\,,\,3\,)\,,\,(\,6\,,\,0\,)\) を通るので
\(\displaystyle \mathrm{\color{red}{AF}}\,:\,\color{red}{y=-\frac{1}{3}x+2}\)
直線 \(\mathrm{\color{green}{AD}}\) は \((\,-3\,,\,3\,)\,,\,(\,0\,,\,-7\,)\) を通るので
\(\displaystyle \mathrm{\color{green}{AD}}\,:\,y=-\frac{10}{3}x-7\)
直線 \(\mathrm{\color{magenta}{BD}}\) は \((\,6\,,\,12\,)\,,\,(\,0\,,\,-7\,)\) を通るので
\(\displaystyle \mathrm{\color{magenta}{BD}}\,:\,\color{magenta}{y=\frac{19}{6}x-7}\)
直線 \(\mathrm{\color{orange}{DF}}\) は \((\,0\,,\,-7\,)\,,\,(\,6\,,\,0\,)\) を通るので
\(\displaystyle \mathrm{\color{orange}{DF}}\,:\,y=\frac{7}{6}x-7\)
交点を求めますが、\(\color{red}{点\,\mathrm{G}}\) の座標がないとどうにも比が出せません。
相似も合同も平行な直線もないので、直接三角形の面積を求めにいった方がはやそうだからです。
\(\color{red}{\mathrm{G}}\) の座標は
直線 \(\mathrm{\color{red}{AF}}\) と 直線 \(\mathrm{\color{magenta}{BD}}\)
の交点です。
\( \begin{cases}
\hspace{7pt} \displaystyle y=-\frac{1}{3}x+2\\ \\
\hspace{7pt} \displaystyle y=\frac{19}{6}x-7
\end{cases}\)
から
\(\displaystyle -\frac{1}{3}x+2=\frac{19}{6}x-7\)
両辺を6倍して
\(\begin{eqnarray}
-2x+12&=&19x-42\\
-2x-19x&=&-12-42\\
-21x&=&-54\\
21x&=&54\\
\displaystyle x&=&\frac{54}{21}=\color{red}{\frac{18}{7}}
\end{eqnarray}\)
この問題に取りかかれているレベルの人にこの計算は必要ないですね。
\(y\) 座標は
\(\displaystyle y=-\frac{1}{3}\times \frac{18}{7}+2\\
\displaystyle =\frac{-6+14}{7}=\color{blue}{\frac{8}{7}}\)
よって \(\color{red}{\mathrm{G}}\) の座標は
\(\displaystyle \left(\,\color{red}{\frac{18}{7}}\,,\,\color{blue}{\frac{8}{7}}\,\right)\)
ここからが面積比の出し方です。
入試の関数でよく出る形の面積の求め方
もう少しなのですがここからが方法が分かれます。
直線になっている部分の線分比から面積比にすると早いのですが、
実際の面積計算で比を出す方が分かり易いでしょう。
関数で三角形の面積を求めるときよく出る形なので覚えておくと良いです。
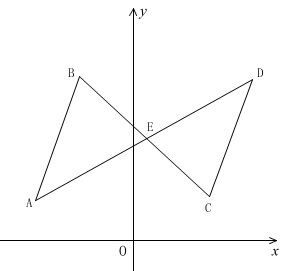
例えば、

この図で三角形 \(\mathrm{OAB}\) の面積を求めるとき、
\(y\) 軸に底辺となる線分 \(\mathrm{OC}\) をとり、
頂点から \(y\) 軸までの距離 \(\mathrm{AD,BE}\) を高さ、
とする二つの三角形の面積の和とする求め方です。
\(\triangle \mathrm{OAB}=\triangle \mathrm{OAC}+\triangle \mathrm{OBC}\)
この場合は線分 \(\mathrm{OC}\) の長さは直線 \(\mathrm{AB}\) の切片として出てきますので分かり易いです。
原点を通らないときでも、同じように軸を切り取る線分を底辺と考えると面積が出てくることが多いです。
問題に戻って見てみましょう。

三角形 \(\mathrm{AGB}\) と三角形 \(\mathrm{DFG}\) の面積を求めるとすると、
底辺にできる線分は見つけにくいですが、
\(\,△\mathrm{AGB}=△\mathrm{DAB}-△\mathrm{DAG}\,\)
とすれば\(\color{red}{底辺を \mathrm{DC}}\) と見ることで求めることが可能です。
または
\(\triangle \mathrm{AGB}=\triangle \mathrm{ABF}-\triangle \mathrm{BGF}\)
とすれば\(\color{red}{底辺を \mathrm{BF}}\) ( \(y\) 軸に平行)と見ることで求めることが可能です。
同じように三角形 \(\mathrm{DFG}\) は
\(\triangle \mathrm{DFG}=\triangle \mathrm{DAF}-\triangle \mathrm{DAG}\)
とするか、
\(\triangle \mathrm{DFG}=\triangle \mathrm{DBF}-\triangle \mathrm{GBF}\)
とすることで面積が求めることができます。
普通なら
\(\triangle \mathrm{AGB}=\triangle \mathrm{DAB}-\triangle \mathrm{DAG}\)
\(\triangle \mathrm{DFG}=\triangle \mathrm{DAF}-\triangle \mathrm{DAG}\)
で考えると思います。
直線 \(\mathrm{AF}\) は求めているので切片から \(y\) 軸上の底辺となる線分の長さはわかりますが、
ここでは線分 \(\mathrm{BF}\) を底辺として見ておきましょう。
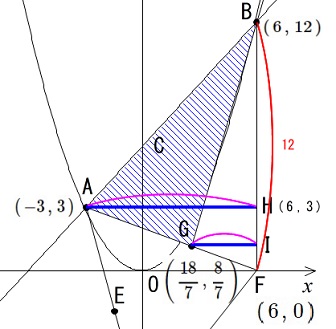
線分 \(\mathrm{BF}\) の長さは2点 \(\mathrm{B,F}\) の \(y\) 座標の差なので
\(\mathrm{BF}=12-0=12\)
高さは \(x\) 座標の差になるので
\(\begin{eqnarray}
\displaystyle \triangle \mathrm{ABF}&=&\frac{1}{2}\times \mathrm{BF}\times \mathrm{AH}\\
\displaystyle &=&\frac{1}{2}\times 12\times \{6-(-3)\}\\
&=&54
\end{eqnarray}\)
\(\begin{eqnarray}
\displaystyle \triangle \mathrm{BGF}&=&\frac{1}{2}\times \mathrm{BF}\times \mathrm{GI}\\
\displaystyle &=&\frac{1}{2}\times 12\times \left\{6-\left(\frac{18}{7}\right)\right\}\\
\displaystyle &=&\frac{1}{2}\times 12\times \frac{42-18}{7}\\
\displaystyle &=&\frac{1}{2}\times 12\times \frac{24}{7}\\
\displaystyle &=&\frac{144}{7}
\end{eqnarray}\)
差を取って
\(\begin{eqnarray}
\triangle \mathrm{AGB}&=&\triangle \mathrm{ABF}-\triangle \mathrm{BGF}\\
\displaystyle &=&54-\frac{144}{7}\\
\displaystyle &=&\frac{378-144}{7}\\
\displaystyle &=&\color{red}{\frac{234}{7}}\\
\end{eqnarray}\)
同じように
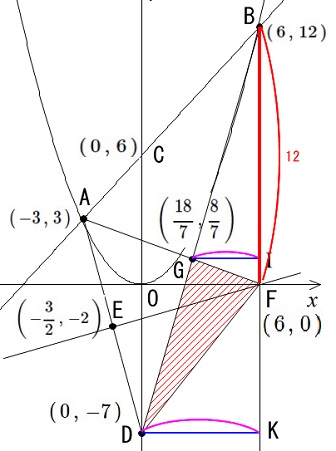
\(\triangle \mathrm{DFG}=\triangle \mathrm{DBF}-\triangle \mathrm{GBF}\)
を利用します。
\(\begin{eqnarray}
\displaystyle \triangle \mathrm{DBF}&=&\frac{1}{2}\times \mathrm{BF}\times \mathrm{DK}\\
\displaystyle &=&\frac{1}{2}\times 12\times \{6-(0)\}\\
&=&36
\end{eqnarray}\)
\(\begin{eqnarray}
\displaystyle \triangle \mathrm{GBF}&=&\frac{1}{2}\times \mathrm{BF}\times \mathrm{GI}\\
\displaystyle &=&\frac{1}{2}\times 12\times \left\{6-\left(\frac{18}{7}\right)\right\}\\
\displaystyle &=&\frac{1}{2}\times 12\times \frac{42-18}{7}\\
\displaystyle &=&\frac{1}{2}\times 12\times \frac{24}{7}\\
\displaystyle &=&\frac{144}{7}
\end{eqnarray}\)
差を取って
\(\begin{eqnarray}
\triangle \mathrm{DFG}&=&\triangle \mathrm{DBF}-\triangle \mathrm{GBF}\\
\displaystyle &=&36-\frac{144}{7}\\
\displaystyle &=&\frac{252-144}{7}\\
\displaystyle &=&\color{red}{\frac{108}{7}}\\
\end{eqnarray}\)
よって
\(\triangle \mathrm{AGB}:\triangle \mathrm{DFG}\\
\displaystyle= \frac{234}{7}:\frac{108}{7}\\
=234:108\\
=\underline{13:6}
\)
答えは出ましたが、交点の座標が分数なので計算に自信が持てなかったかもしれませんね。
普通 \(y\) 軸を底辺とする場合で計算するので逆でしょうけど、
\(y\) 軸上の \(\mathrm{DC}\) を底辺とした場合の面積比で検算しても良いですね。
いずれにしても、図を横に見ながら進めればここで説明を見るよりはやりやすいです。
自分でわかる限りの情報を見やすく書いて、ときには抜き出した図を書いて、
自信を持って計算を進め、見直しをする。
それしかありません。
ずるい面積比の求め方
一つだけ、超え太郎(中学数学を超えた)マスター向きの解き方を簡単にですがお伝えして終わります。
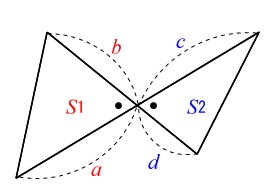
図のように一つの角が等しいとき、
(直線が交わるときは対頂角が等しいので今回の問題でも同じことがいえます。)
その等しい角をはさんでいる二つの辺の積の比が面積比になります。
\(\large{\color{red}{S_1}\,:\,\color{blue}{S_2}\,=\,\color{red}{ab}\,:\,\color{blue}{dc}}\)
今回の問題に当てはめてみましょう。
線分の長さは必要ありません。
線分比だけで良いので \(x\) 座標か \(y\) 座標のどちらかの差を線分比としてかまいません。
「何故線分の長さじゃなくて、各座標の差で良いのか?」
素晴らしい質問です。
質問内容ではありません。
単なる流し読みではなくしっかり解きながらやっているからこその質問ですね。
「鉛筆動かしながらじゃないと過去問は意味ないよ」、といっている私なんかの言葉もくみ取ってくれている。
ありがたいことです。
そしてこれをやっている人は高校数学でも力が発揮できます。
たかがセンタ-試験や共通テストで8割、9割も取れない人の理由はこれをやっていないからです。
その違いは大きいですよ。3年後に実感して下さい。
説明します。
面積そのものを求めるときは長さは必要ですが、面積比の場合は線分比だけで出すことができます。
怪しい人はかなり時間に差は出ますが、三平方の定理で実際の長さで面積比を出しても良いですよ。
面積比だから線分比で良いので
\(\,\mathrm{△AEB:△DEC=AE\times BE:DE\times CE}\,\)
ここまでは良いとして、
線分比じゃなくて\(\,x\,\)座標の差、
または\(\,y\,\)座標の差の比で良い
という部分です。
実はこれは公立入試でも良く取り上げられることで、
高さの比を利用した面積を求める問題に使うことが多いです。
ここでは
\(\,\color{red}{\mathrm{AE:DE}=(\,\mathrm{AE}\,の\,x\,座標の差):(\,\mathrm{DE}\,の\,x\,座標の差)}\,\)
または
\(\,\color{red}{\mathrm{AE:DE}=(\,\mathrm{AE}\,の\,y\,座標の差):(\,\mathrm{DE}\,の\,y\,座標の差)}\,\)
の部分を説明します。
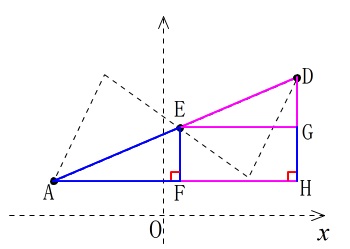
線分\(\,\mathrm{AD}\,\)だけを抜き出して考えてみましょう。

\(\,\mathrm{A,E,D}\,\)から軸に平行線を引いて直角三角形\(\,\mathrm{AHD}\,\)を作ります。
すると
\(\,\mathrm{△AEF}\,\) ∽ \(\,\mathrm{△ADH}\,\)
はすぐに分かると思いますが、相似なので対応する辺の比はそれぞれ等しくなります。
さらに一歩進んで、
\(\,\mathrm{EF\,/\!/\,DH}\,\)なので
\(\,\mathrm{\color{red}{AE}:\color{red}{ED}=\color{blue}{AF}:\color{blue}{FH}}\,\)
\(\,\mathrm{AH\,/\!/\,EG}\,\)なので
\(\,\mathrm{\color{red}{AE}:\color{red}{ED}=\color{magenta}{HG}:\color{magenta}{GD}}\,\)
つまり、
線分比は\(\,x\,\)座標の差、
または\(\,y\,\)座標の差と同じ
だということです。
この比を利用する問題はあちこちの都道府県で面積を求めるときに出ていますので、
相似の単元の復習をしておくと良いですよ。
直接の面積計算ではなく、分かり易い面積があるときの一部の面積を求めるときなどに使います。
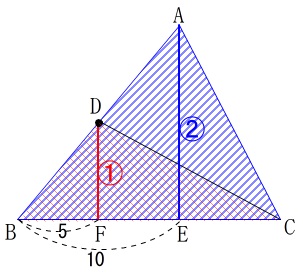
この図の様に
\(\,\displaystyle \mathrm{△BDC=\frac{1}{2}\times △ABC}\,\)
となることを利用するということです。
図形問題としては簡単なのですが、座標上にあるので使えない人が多いですけどね。
関数の問題だから図形の知識を使っちゃいけないとか、数学はそんなに狭い心は持っていません。笑
問題作成者は関数、座標の中で相似を試しているのです。
ここでは \(x\) 座標でやっておきます。
\(y\) 座標の方は少し分子が小さくなるのでやりやすいから自分でやってみて下さい。
\(\begin{eqnarray}
\color{blue}{\triangle \mathrm{AGB}}\,:\,\color{red}{\triangle \mathrm{FGD}}\,&=&\,\color{blue}{\mathrm{AG}\times \mathrm{BG}}\,:\,\color{red}{\mathrm{FG}\times \mathrm{DG}}\\ \\
\displaystyle &=&\color{blue}{\left\{\frac{18}{7}-(-3)\right\}\times \left\{6-\left(\frac{18}{7}\right)\right\}}\,:\,\color{red}{\left\{6-\left(\frac{18}{7}\right)\right\}\times \left(\frac{18}{7}-0\right)}\\ \\
\displaystyle &=&\color{blue}{\frac{18+21}{7}\times \frac{42-18}{7}}\,:\,\color{red}{\frac{42-18}{7}\times \frac{18}{7}}\\ \\
\displaystyle &=&\color{blue}{\frac{39}{7}\times \frac{24}{7}}\,:\,\color{red}{\frac{24}{7}\times \frac{18}{7}}\\ \\
&=&\color{blue}{13}\,:\,\color{red}{6}
\end{eqnarray}\)
これは高校生でも見抜きにくいかもしれませんが、超え太郎マスターは当たり前の解法になっていると思います。
中学生に無理しろとはいいませんが、過去に数学が苦手といっていた中学生が、1ヶ月でこのレベルにまでなったのは一人や二人ではありません。
中学生の伸びしろがどれだけ大きいか思い知らされます。
あなたにも可能性はあるのです。
何故なら、道具はすべて会員サイトにありますから。
⇒ 神奈川県公立高校入試問題(平成30年度)の数学の過去問解説(問1~問3)
問1から問3はまとめて説明しています。
⇒ 神奈川県公立入試2018年(平成30年)の数学問5確率問題の解説
問5は確率です。ルールの読み取りが大切なのは確率だけではありませんが大きなポイントになります。
