東京都立高校入試2018(平成30年度)前期 数学問題の解説(問1)

東京都の公立（都立）高校入試2018(平成30年度)に前期日程で行われた数学の問題と解答解説です。
ここでは大問1の問9までの解説になります。
大問１は全体で５分もかからない小問集合問題ですが、確実に取っておきたいところなので注意することは小さなことが１つ、大きな注意点が一つです。

問題は東京都の公式ホームページにもあります。

⇒　2018東京都立高校入試前期の数学問題

都立入試の注意点

都立高校を受験するときの注意点と準備するものです。

まずは小さな注意点。（大きな注意点は最後にまとめます。）
都立高校の数学問題は親切に問題の注意書きが多いです。
２０１８年で１３項目あります。

毎年大きく変わることではありませんのであらかじめ目を通しておくことをおすすめします。
試験開始までに目を通す時間はありますが、項目数が変わっている場合は必ずチェックしておきましょう。

準備するもの、これは受験票が届くまでに確認していることですが、
作図があるのでコンパスは必要です。

筆記用具も当然ですが、都立高校入試ではマークシート方式が一部入ります。
マークシートのポイントはマークすることに時間をかけないことです。

学校の先生に言われているとは思いますが、ここでも言っておきます。

HBまたはBのシャーペンでも良いと書かれていますが、マーク用の鉛筆と両方用意しましょう。
普通の計算部分や下書き段階はシャーペンでかまいませんが、マークするときは鉛筆を使うのです。

鉛筆は芯が少し太いBを用意することをおすすめします。
HBよりBの方が濃いだけでなく、芯が柔らかいので間違えたとき消しやすいです。

鉛筆の削った先を少し平らにしておくとマークの時間は少し減ります。
マークする番号を丸く縁取って、後は中を塗りつぶすのですが、太い方がはやいです。

問題が全体通して短い時間で解ける構成になっているし、
マークする部分が少ないのでシャーペンでも良いですけどね。

シャーペンの芯まで口出しする気はないですが、笑
HBよりはBの方が消した後が残りにくいです。
これは都立に限ったことではありません。

では\(\color{black}{\fbox{ 1 }}\)の解説に入ります。

『覚え太郎』会員にとっては単純作業で答えが出ます。
目安は５分です。
ここだけで配点が\(\,46\,\)点あることを知っておくと良いです。

解説は一般向けになるので長くなります。笑

正負の数と文字式と無理数の計算問題

\(\,問1\,\)　正負の数の計算問題です。

かけ算割り算が足し算引き算より先、というのは算数と変わりません。

　\(\displaystyle \hspace{10pt}5-\frac{1}{3}\times (-9)\\
=5-(-3)\\
=5+3\\
=\underline{8}\)

2行目は省略しても良いですが、3行目は書いた方がはやいしミスが減ります。

暗算の方が速いと感じるのはわかります。
でも、この程度なら差はありませんが項が多くなる計算では逆に遅くなりますよ。
そもそも、書いても時間かからないのに書かない理由が見つかりません。

会員にいっておきますが、高校に行っても数学を苦手にしたくないならレポートで指摘している計算は続けた方が良いです。

\(\,問2\,\)　文字式の展開と整理です。

　\(\hspace{10pt}8(a+b)\color{red}{-(4a-b)}\\
=8a+8b\color{red}{-4a+b}\\
=\underline{4a+9b}\)

これも2行目は省略しないことです。
この１行を飛ばすことでのミスが非常に多いです。

見直しで気がつくでしょうが、暗算してミスすることで逆に時間の無駄になりますので、手間と時間のかからない１行の重要性を認識しておくと良いです。

\(\,問3\,\) 無理数の展開計算です。

分母の有理化が混じっていないので説明が楽です。笑

この展開は公式を使うとすぐに答えが出ます。
この程度の練習はさんざんやってきたと思いますが、最悪一つひとつ展開すれば答えは出ますよ。

展開公式
　\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用すると

　\(\hspace{10pt}(\sqrt{7}+2\sqrt{3})(\sqrt{7}-2\sqrt{3})\\
=(\sqrt{7})^2-(2\sqrt{3})^2\\
=7-4\times 3\\
=7-12\\
=-5\)

展開してもしれてますので本番ではあがきましょう。笑
公式使えても展開するというのも確実性を増す見直しになります。

　\(\hspace{10pt}(\sqrt{7}+2\sqrt{3})(\sqrt{7}-2\sqrt{3})\\
=\sqrt{7}\times \sqrt{7}-\sqrt{7}\times 2\sqrt{3}+2\sqrt{3}\times \sqrt{7}-2\sqrt{3}\times 2\sqrt{3}\\
=7-2\sqrt{21}+2\sqrt{21}-4\times 3\\
=7-12\\
=\underline{-5}
\)

この計算でも2行目は2段階の暗算はしていませんので省略してもかまいません。

１次方程式と連立方程式と２次方程式

\(\,問4\,\) １次方程式を解きます。

方程式を解くことと方程式の解を求めることは同じことですよ。

基本通り左辺に\(\,x\,\)の項を集め、右辺に定数項を集めます。

　\(\begin{eqnarray}
4x-5&=&x-6\\
4x-x&=&-6+5\\
3x&=&-1\\
x&=&\displaystyle \underline{-\frac{1}{3}}
\end{eqnarray}\)

ここでも移項の説明をしておきます。

　\(\begin{eqnarray}
4x\color{blue}{-5}&=&\color{red}{x}-6\\
4x\color{red}{-x}&=&-6\color{blue}{+5}\\
\end{eqnarray}\)

２つ一度に移項しているので見にくいですが、

　\(\begin{eqnarray}
4x-5\color{blue}{+5}&=&x-6\color{blue}{+5}\\
4x&=&x-6+5\\
4x\color{red}{-x}&=&x\color{red}{-x}-6+5\\
4x-x&=&-6+5
\end{eqnarray}\)

左辺の\(\,-5\,\)を消すために両辺に\(\,\color{blue}{+5}\,\)を足して、
右辺の\(\,x\,\)を消すために両辺に\(\,\color{red}{-x}\,\)を足す、
その結果、移項すると符号が入れ替わっているのです。

\(\,問5\,\) 普通の連立方程式を解くだけの問題です。

　\( \begin{cases}
\hspace{7pt} 7x-y=8\\ \\
\hspace{7pt} -9x+4y=6
\end{cases}\)

連立方程式を解くときの方針は一文字消去です。
ここでは\(\,y\,\)を消去することを考えます。

消去するのはどちらでも良いですが、\(\,x\,\)を消去しようとすると両方の方程式を何倍かしなくてはなりません。
\(\,y\,\)だと上の方程式を4倍すれば係数がそろいます。

上の方程式を両辺4倍すると
　\(28x-4y=32\)

この方程式と下の方程式を辺ごとに足すと

　\(\hspace{19pt}28x-4y=32\\
+\underline{)\,-9x+4y=\hspace{6pt}6　}\\
\hspace{18pt}19x\hspace{22pt}=38\\
\hspace{50pt}x=\underline{2}\)

連立方程式ではもう一つも求めておくことを忘れないようにしましょう。
解答用紙見たらすぐ気がつきますけどね。

この\(\,x=2\,\)をどの方程式でもいいので代入して\(\,y\,\)を求めます。
一番上の方程式に代入しましょう。

　\(\begin{eqnarray}
7(2)-y&=&8\\
14-y&=&8\\
-y&=&8-14\\
-y&=&-6\\
y&=&\underline{6}
\end{eqnarray}\)

　答え　\(x=2\)　,　\(y=6\)

\(問6\)　2次方程式を解きます。

　\(x^2+12x+35=0\)

2次方程式を解くことと、2次方程式の解を求めることは同じですよ。

だからといって解の公式をいつも使うわけではありません。
２次方程式を因数分解して解けないかをまずは試してみることをおすすめします。
特に文章題は整数解が多いので、ほとんどが因数分解できます。

２次方程式を解く手順としては、項をすべて左辺に集めて右辺を\(\,0\,\)にすることからです。
この問題ではその手間すら省いてくれています。

次は定数項に着目して因数分解を試みます。
定数項は+35なのでかけて35になる整数の組み合わせを書き出します。
　\(\color{black}{\fbox{ 1×35 }}\)　\(\color{red}{\fbox{ 5×7 }}\)
この\(\,2\,\)つだけですが、足すか引くかで\(\,x\,\)の1次の項の係数\(\,+12\,\)になる組み合わせを探します。

かけて\(\,＋35\,\)なので両方＋か両方－です。
　\(\,+5\,\)と\(\,+7\,\)の組み合わせで\(\,+12\,\)となるので

　\(\begin{eqnarray}
x^2+12x+35&=&0\\
(x+5)(x+7)&=&0\\
x&=&\underline{-5\,,\,-7}
\end{eqnarray}\)

小問集合での2次方程式は解の公式を使うことが多いので、解の公式は覚えておきましょう。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

資料の整理(度数分布表)

度数分布表がありますが、4月7日とか40年間とかは関係ありません。
40日分の気温を測ったデータが度数分布表になっているのと同じです。

　\(\hspace{10pt}階級(℃)\hspace{30pt}度数(日)\\
　以上\hspace{20pt}未満\\
\hspace{10pt}8　～　10\hspace{35pt}1\\
\hspace{4pt}10　～　12\hspace{35pt}4\\
\hspace{4pt}12　～　14\hspace{35pt}2\\
\hspace{4pt}14　～　16\hspace{35pt}7\\
\hspace{4pt}16　～　18\hspace{35pt}8\\
\hspace{4pt}18　～　20\hspace{35pt}\color{red}{5}\\
\hspace{4pt}20　～　22\hspace{35pt}\color{red}{9}\\
\underline{\hspace{4pt}22　～　24\hspace{35pt}\color{red}{4}\hspace{10pt}　}\\
\hspace{20pt}計\hspace{50pt}40
\)

\(\,18\,\)℃以上だった日は
　\(5+9+4=18日\)
度数合計が\(\,40\,\)なので
　\(\displaystyle \hspace{10pt}\frac{18}{40}\times 100\\
=\underline{45}％\)

これはちょっと簡単すぎるので来年以降はもう少し違った形になってくると思われますね。

この問題はたまたま用語を知らなくても出せる問題だっただけだということは覚えておきましょう。
資料の整理では用語を覚えていないと通用しないのが普通です。

平行線と角度

基本的な平行線の角度の問題です。

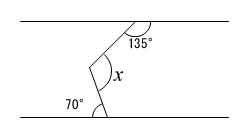
条件は図の角度と \(\ell\, //\, m\) だけです。

すぐに2つの見方ができますが、平行線でカクカクと曲がったときにも使いやすい方から説明します。

曲がったところで平行線を引くと錯角が等しいので、図のように等しい角度が次々とつながります。

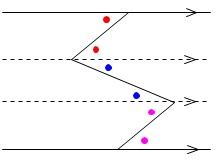
この方法で平行線を引くと

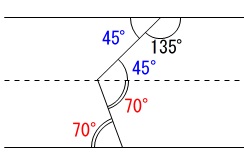
これから
　\(x=45^{\circ}+70^{\circ}=\underline{115^{\circ}}\)

右上の角度\(\,135°\,\)をそのまま使わない点は注意が必要です。

もう一つは三角形を作って内角の和や外角の性質を利用します。
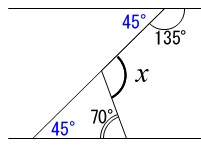わかる角度を一つずつ書いていけばでます。
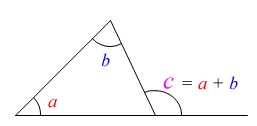図の　\(c=a+b\) を使えばはやいですね。
　\(x=45^{\circ}+70^{\circ}=\underline{115^{\circ}}\)

　答えは　\(\,\underline{115}\,度\,\)

作図

折り目の作図です。

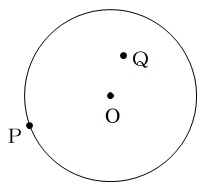
　点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)が重なるように折り曲げた折り目を作図しなさい。
という問題です。

2点が重なる折り目は「垂直二等分線」です。
　「線分\(\,\mathrm{PQ}\,\)の垂直二等分線を作図しなさい。」
と問題を置きかえることができます。

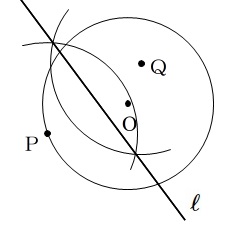
作図のポイントはコンパスの針の指しどころですよ。

直線 \(\ell\) という文字も書くように指示がありますので、問題の指示はよく見るようにしましょう。

直線\(\,\ell\,\)は線分\(\,\mathrm{PQ}\,\)の垂直二等分線ですが、線分\(\,\mathrm{PQ}\,\)を結ぶ必要はありません。
書いても減点はされないと思いますが、必要最小限の作図をするようにしておくといいです。
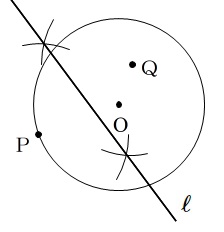弧を書くとき図のように重なる部分だけで良いです。
しかし、ちょんちょん、と一部の弧を書くより、バン！と書いた方が確実に交差する部分が出てきやすいです。

こういうのを説明していて感じるのは、
　図は多くのことを語る
ということですね。

日本語の説明がほとんどいらなくなります。
でも、図を書いて挿入するのに時間かかりますけど。ｗ

作図の解答も「日本語なし」ですよね。

都立入試での大きな注意点と対策

ここで大きな注意点ですが、
\(\color{black}{\fbox{ 1 }}\)は難しい問題がありません。

教科書の基本さえおさえてあればとれる問題で時間もかかりません。

狙っている点数が何点かによりますが、まずは\(\,6\,,\,7\,\)割と考えているなら、
この\(\color{black}{\fbox{ 1 }}\)の配点を見直してみてください。

公立高校入試ではどこも同じで当たり前のことですが、
教科書の基本を広くおさえていくことが一番の対策になります。

　\(\color{magenta}{\fbox{会員に向けて}}\)
『覚え太郎』と『基礎レポート』で十分な範囲ですよ。
問題を最後まで見ればわかりますが、満点狙えます。
もちろん『超え太郎』の一部でもあればもっと楽ですけど。笑
入試前はもう一度基本編を見直しておきましょう。

解答の記述含めてかなり時間が余るでしょう。
その後の大切なこと忘れないように！

⇒　2018年東京都公立高校入試の前期大問2立体図形の問題と解説

『覚え太郎』に慣れている人は大問\(\,2\,\)を普通に考えると余計なことをしてしまいます。
もっと簡単に考えてください。

⇒　東京都公立高校入試数学の過去問と解答解説

都立高校入試の数学過去問解説まとめページです。