2018年東京都公立高校入試の前期大問2立体図形の問題と解説

2018年に東京都で行われた公立入試の前期大問2の問題と解説です。
大問2は立体図形に関する問題です。
立体といっても総合ではなく1年の空間図形の内容で解ける問題だけです。

問題は東京都が公開してくれています。

⇒　東京都2018前期数学問題　

六角柱の表面積

　\(\color{black}{\fbox{ 2 }}\)　
\(\,問1\,\)は六角柱の表面積です。

これは会員であればすぐにやらなければならない作業がわかるでしょう。
ただ、問題が簡単すぎて先走るとやり直すことになります。笑
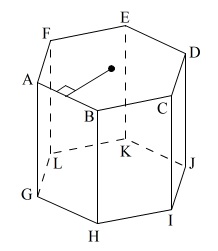この\(\,図Ⅰ\,\)が問題に与えられています。
問題の条件です。
短めの文章がありますが、条件を書き出すともっとすっきりします。

　立体は正六角柱
　底面の\(\,1\,\)辺は\(\,\color{red}{a}\,\)
　高さが\(\,\color{red}{h}\,\)
　\(\,\mathrm{MN}=\color{red}{b}\,\)
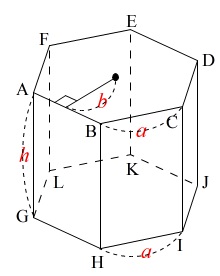ここまでは文章通りなのですぐ終わります。

表面積を求めます。
表面積とあれば展開図です。
球以外は展開図が書けるので、展開図を書くことで平面で考えることができます。
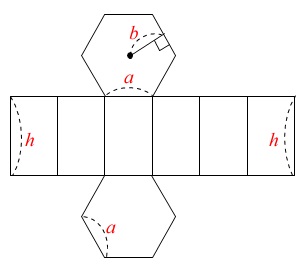長方形部分は簡単に面積は出ます。
正六角形のときは対角線を入れるとほとんどの問題が楽になるのでポイントになるのですが、
この問題では親切に問題が誘導してくれています。

　\(\,\mathrm{AD}と\mathrm{CF}の交点が\mathrm{M}\,\)

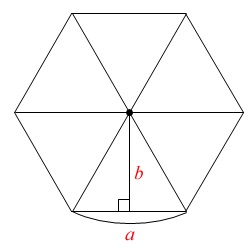正六角形は\(\,\color{red}{正三角形\,6\,つ分}\,\)です。

ここで正三角形の高さを三平方の定理で求めるのが普通ですが、
この問題は高さ\(\,b\,\)として求めます。
底辺は正六角形の\(\,1\,\)辺\(\,a\,\)なので
　
　\(\hspace{10pt}(正六角形の面積)\\
\displaystyle =\frac{1}{2}\times a\times b\times 6\\
=3ab\)

この底が\(\,2\,\)つあるので

　\(\hspace{10pt}(底面＋底面)\\
=2\times 3ab\\
=\color{red}{6ab}\)

側面は縦が高さ\(\,h\,\)で横は\(\,6a\,\)になるので

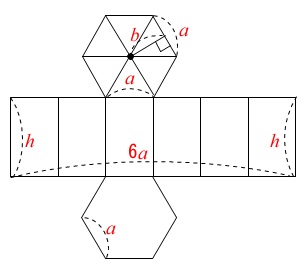
　\(\,(側面)=\color{blue}{6ah}\,\)

よって表面積\(\,\mathrm{P}\,\)は

　\(\begin{eqnarray}
\mathrm{P}&=&\color{red}{6ab}+\color{blue}{6ah}\\
&=&6a(\,\underline{b+h}\,)
\end{eqnarray}\)

三平方の定理を使って\(\,b\,\)を\(\,a\,\)で表すこともできますがここでは聞いていませんでした。
　

円柱の表面積

問\(\,2\,\)は円柱の表面積です。

問題に与えられた文字を図に書き込んでみると
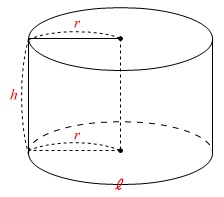立体は立体のまま考えません。
展開図を書き出します。

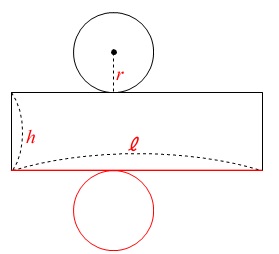
解答用紙に示す必要がない場合は簡単にフリーハンドで良いですよ。
このときポイントは円周と長方形の横\(\,\ell\,\)の長さが一致することです。

問題は何を聞いているかというと、

　表面積\(\,\mathrm{Q}\,\)が
　　\(\,\mathrm{Q}=\ell (h+r)\,\)

となることを証明することです。

こういう証明はどうやってと考える前に、わかる関係式をいくつか出せば終わっているのことが多いです。
すぐにわかるのではなく、わかることを書き出してみると見えてくるのです。

\(\,\ell\,\)は半径\(\,r\,\)の円周なので
　\(\,\ell=2\pi r\,\)

底面の円の面積は\(\,\color{red}{\pi r^2}\,\)です。
側面の長方形の面積は縦は高さが\(\,h\,\)、横は円周と同じ\(\,\ell\,\)なので

　\(\,(側面の面積)=\color{blue}{h\ell}\,\)

これから円柱の表面積Qは底面が2つあることに注意して

　\(\,\mathrm{Q}=2\color{red}{\pi r^2}+\color{blue}{h\ell}\,\)

証明すべき関係式と違うのは\(\,2\pi r^2\,\)の部分ですが、
　\(\,\color{red}{\ell}=\color{magenta}{2\pi r}\,\)
なので

　\(\begin{eqnarray}
\mathrm{Q}&=&2\pi r^2+h\ell\\
&=&\color{magenta}{2\pi r}\times r+h\ell\\
&=&\color{red}{\ell} \times r+h\ell\\
&=&\ell(r+h)
\end{eqnarray}\)

と証明できます。

これをきれいにまとめると、
（答え）
\(\,\ell\,\)は半径\(\,r\,\)の円周に等しいので
　\(\,\underline{\ell=2\pi r}\,\)

（証明）
底面の円の面積は　\(\,\pi r^2\,\)

側面の長方形の面積は縦は高さが\(\,h\,\)、横は円周と同じ\(\,\ell\,\)なので
　\(\,(側面の面積)=h\ell\,\)

よって円柱の表面積\(\,\mathrm{Q}\,\)は底面積2つと側面積の和だから
　\(\begin{eqnarray}
\mathrm{Q}&=&\pi r^2+\pi r^2+h\ell\\
&=&2\pi r^2+h\ell
\end{eqnarray}\)

ここで円周\(\,\ell\,\)は
　\(\,\ell=2\pi r\,\)
なので

　\(\begin{eqnarray}
Q&=&2\pi r^2+h\ell\\
&=&2\pi r\times r+h\ell\\
&=&\ell r+h\ell\\
&=&\ell(r+h)　（終わり）
\end{eqnarray}　\)

1年の空間図形と文字式の証明でした。

⇒　東京都立高校入試2018(平成30年度)前期 数学問題の解説(問1)

ここまでで\(\,58\,\)点分です。

⇒　2018年東京都公立高校入試前期試験の大問3関数の解説

問3は関数問題です。