2022年度東京都立高校入試前期の数学第４問平面図形の問題と解説

2022年(令和4年)度東京都公立高校入試問題【前期】の数学第４問の問題と解説です。
第４問は平面図形問題です。
正三角形２つを合わせたひし形なので平行四辺形の条件を利用します。
同位角や錯角が等しくなる基本は必ず確認しておきましょう。

前半部分は下部にリンクさせてあります。

2022年(令和4年)度東京都公立高校入試問題前期の数学第４問の問題

問題は前半部分にもありますが、
第４問分だけを再度載せておきます。

\(\color{black}{\fbox{4}}\)の問題　⇒　2022年(令和4年)度東京都公立高校入試【前期】の数学第4問の問題PDF

表紙の注意書きおよびマークシートは添付していません。

2022年(令和4年)度東京都公立高校入試【前期】の数学第4問の解説

\(\color{black}{\fbox{4}}\)の平面図形問題の解説です。

\(\color{black}{\fbox{4}}\)
正三角形が2つ組み合わされた平面図形の問題です。
問題に書かれていませんが平行四辺形（ひし形）ですね。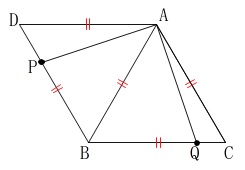点\(\,\mathrm{P\,,\,Q}\,\)は頂点にはありません。

〔問１〕角度を文字を使って表す問題

角度を文字を使って求めます。
　\(\,\mathrm{∠PAQ}=90^{\circ}\,,\,\mathrm{∠DAP}=a^{\circ}\,\)
とするときの\(\,\mathrm{∠AQB}\,\)の大きさです。
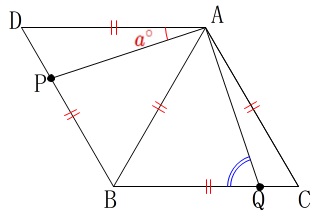正三角形が２つなので色々考えられるでしょう。
いくつか経路は出てきますがどれでも良いですよ。
　\(\hspace{10pt}\mathrm{∠DAP}=\color{red}{a^{\circ}}\,\)
なので
　\(\hspace{10pt}\mathrm{∠APB}=60^{\circ}+\color{red}{a^{\circ}}\,\)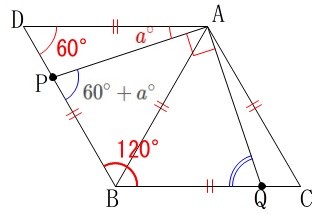四角形\(\,\mathrm{APBQ}\,\)の内角の和は\(\,360°\,\)なので
　\(\hspace{10pt}\mathrm{∠AQB}=\underline{　(\,90-a\,)度　}　\)
（計算は自分でやってみてください。）
※
　\(\hspace{10pt}\mathrm{∠PAQ=}90^{\circ}\)
　\(\hspace{10pt}\mathrm{∠PBQ}=120^{\circ}\)
なので四角形の内角の和の残りが\(\,150°\,\)だから
　\(\hspace{10pt}\mathrm{∠APB+∠AQB}=150°\)
となります。

\(\color{black}{\fbox{1}}\)の〔問８〕でも出てきていますが、
　\(\hspace{4pt}\mathrm{∠APB=∠ADP+∠DAP}\)です。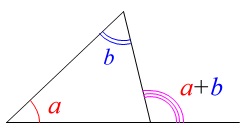または、
　\(\,\mathrm{∠DAC=120^{\circ}}\,,\,\mathrm{∠PAQ}=90^{\circ}\)
なので
　\(\hspace{4pt}\mathrm{∠CAQ}=\color{blue}{30^{\circ}-a^{\circ}}\)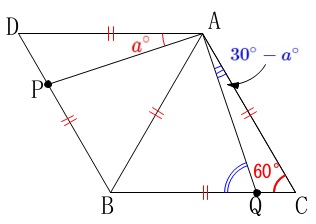だから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AQB}&=&\mathrm{∠CAQ+∠ACQ}\\
&=&\color{blue}{30^{\circ}-a^{\circ}}+\color{red}{60^{\circ}}\\
&=&(\,90-a\,)^{\circ}
\end{eqnarray}\)
でも良いですし、すべての角が\(\,a\,\)で表せるのでどれでも良いです。
大切なのは、自分で分かる角度を書き込むことです。

〔問２〕合同の証明と面積比

〔問１〕の条件とは異なり\(\,\mathrm{∠PAQ=60^{\circ}}\,\)となります。
なんとなく\(\,\mathrm{△APQ}\,\)は正三角形かな？と思えます。
ただ、理由も無く思い込んではいけませんよ。

\(\,\mathrm{△APQ}\,\)は1つの角が\(\,60°\,\)なので二等辺三角形になれば正三角形です。
それが問題になっています。

①合同の証明

　\(\,\mathrm{△ABP}\,\)≡\(\,\mathrm{△ACQ}\,\)の証明です。

合同の証明のとりあえずの目標は合同条件をそろえることです。
合同条件は5つあるので必ず確認しておいてください。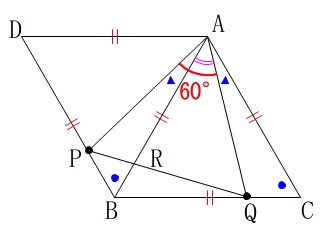会員の方には言うまでもありませんが、
証明を書くときは図の中で証明を済ませてから、です。
（証明）
　\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△ACQ}\,\)において
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ABD}\,\)はともに正三角形で１辺を共有しているので
（「仮定より」で良いです。）
　\(\hspace{4pt}\mathrm{AB=AC}　･･･㋐\)
　\(\hspace{4pt}\mathrm{∠ABP=∠ACQ}=60^{\circ}　･･･㋑\)
また仮定から\(\,\mathrm{∠PAQ=60^{\circ} }\,\)なので
　\(\hspace{4pt}\mathrm{\color{blue}{∠BAP}=60^{\circ}-\color{magenta}{∠BAQ}}　･･･㋒\)
　\(\hspace{4pt}\mathrm{\color{blue}{∠CAQ}=60^{\circ}-\color{magenta}{∠BAQ}}　･･･㋓\)
\(\,㋒㋓\,\)より
　\(\hspace{4pt}\mathrm{∠BAP=∠CAQ}　･･･㋔\)
\(\,㋐㋑㋔\,\)より
　１組の辺とその両端の角がそれぞれ等しい。
よって、
　\(\hspace{10pt}\mathrm{△ABP}\,\)≡\(\,\mathrm{△ACQ}\)
（終わり）

\(\,㋒㋓\,\)を示すときに
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BAP}&=&\mathrm{\color{red}{∠PAQ}}-\mathrm{\color{magenta}{∠BAQ}}\\
&=&\color{red}{60^{\circ}}-\mathrm{\color{magenta}{{∠BAQ}}}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{∠CAQ}&=&\mathrm{\color{red}{∠BAC}}-\mathrm{\color{magenta}{∠BAQ}}\\
&=&\color{red}{60^{\circ}}-\mathrm{\color{magenta}{{∠BAQ}}}
\end{eqnarray}\)
と書いた方がていねいですが、
「仮定」、「正三角形」と何度も言うのもしつこいかなと思い省きました。
（もちろん試験ではできるだけ詳しく書いた方が良いです。）

②2つの三角形の面積比

2つの三角形の面積比を求めます。

「\(\,\mathrm{△BRP}\,\)の面積は\(\,\mathrm{△ABC}\,\)の何倍か？」
と
「\(\,\mathrm{△BRP}\,\)：\(\,\mathrm{△ABC}\,\)は？」
という問題は同じになります。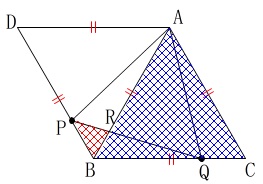\(\,\mathrm{△ABC}\,\)を\(\,1\,\)とすると\(\,\mathrm{△BRP}\,\)の面積がいくつになるかということです。

具体的な長さがないので比で出すしかありません。
※
長さに関係なく成り立つことなので
適当に長さを設定しても答えは出ます。

平行四辺形があるので相似を見つけましょう。
直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{PQ}\,\)の交点を\(\,\mathrm{S}\,\)とします。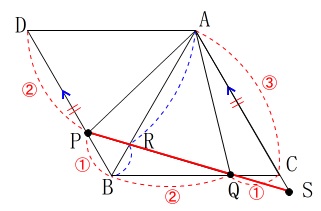

ここで2つの相似があるので書き出します。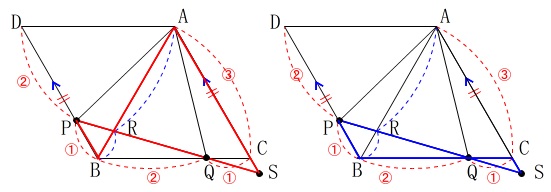　\(\,\mathrm{△ARS}\,\)∽\(\,\mathrm{△BRP}\,\)
　\(\,\mathrm{△BQP}\,\)∽\(\,\mathrm{△CQS}\,\)
相似比を出したいですが、
なぜ相似に着目しているかを説明しますので後にします。

\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ABD}\,\)は合同な正三角形で面積が同じなので
\(\,\mathrm{△ABP}\,\)の面積は\(\,\mathrm{△ABC}\,\)の\(\,\displaystyle \color{green}{\frac{1}{3}}\,\)です。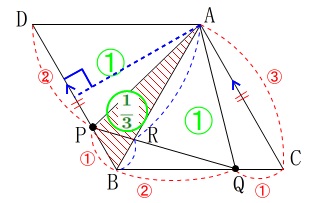高さは共通で底辺が\(\,\displaystyle \frac{\color{red}{①}}{\color{red}{②}+\color{red}{①}}=\color{red}{\frac{1}{3}}\,\)だからです。
（問\(\,①\,\)で示した合同から\(\,\mathrm{△ACQ}\,\)からでも同じです。）
ここで\(\,\mathrm{AR:BR}\,\)が分かれば面積比が出るという方向性が見えてきますね。

それでは相似比を出して行きます。
　\(\,\mathrm{△ARS}\,\)∽\(\,\mathrm{△BRP}\,\)
の相似比は\(\,\mathrm{CS}\,\)の比がわかっていないので後です。

　\(\,\mathrm{△BQP}\,\)∽\(\,\mathrm{△CQS}\,\)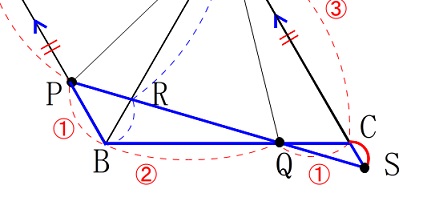からは相似比が
　\(\hspace{10pt}\mathrm{BQ:CQ}=\,2：1\,\)
とすぐに分かるので
　\(\,\mathrm{BP=1}\,\)に対して\(\,\mathrm{CS}=\displaystyle \color{red}{\frac{1}{2}}\,\)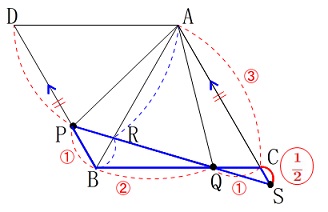これから\(\,\mathrm{BP=1}\,\)に対して
　\(\begin{eqnarray}\displaystyle
\mathrm{AS}&=&\mathrm{AC+CS}\\
&=&3+\frac{1}{2}\\
&=&\color{red}{\frac{7}{2}}
\end{eqnarray}\)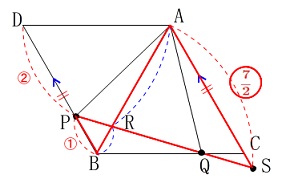となるので
　\(\begin{eqnarray}\displaystyle
\mathrm{AR:BR}&=&\frac{7}{2}:1\\
&=&\Large{\color{blue}{⑦}:\color{blue}{②}}
\end{eqnarray}\)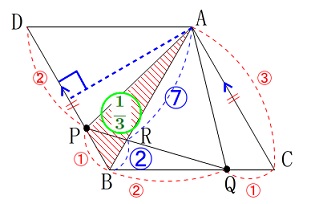よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△BRP}&=&\mathrm{△ABC}\times \frac{1}{3}\times \frac{2}{7+2}\\
&=&\mathrm{△ABC}\times \color{red}{\frac{1}{3}}\times \color{blue}{\frac{2}{9}}\\
&=&\underline{　\frac{2}{27}　}\times \mathrm{△ABC}
\end{eqnarray}\)

相似比の出し方が不安な人は過去の都立入試解説でも
お腹いっぱいになるほどしていますので確認してください。
これからの高校入試でも大学入試でも必ず必要になります。
あえてここではしません。
※
メンドクサイからではありません。

②2つの三角形の面積比（別解）

\(\,\mathrm{P}\,\)から直線\(\,\mathrm{BC}\,\)に垂線を下ろして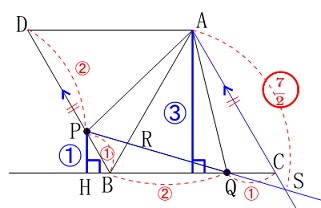高さ\(\,\mathrm{PH}\,\)が\(\,\mathrm{△ABC}\,\)のが\(\,\displaystyle \color{blue}{\frac{1}{3}}\,\)で、
底辺が\(\,\displaystyle \color{red}{\frac{2}{3}}\,\)（\(\,\mathrm{BQ:CQ=2:1}\,\)から）なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△PBQ}&=&\frac{2}{3}\times \frac{1}{3}\times \mathrm{△ABC}\\
&=&\frac{2}{9}\times \mathrm{△ABC}
\end{eqnarray}\)

ここで\(\,\mathrm{PR:RQ}\,\)が知りたいので
線分\(\,\mathrm{PS}\,\)を抜き出し人もいると思います。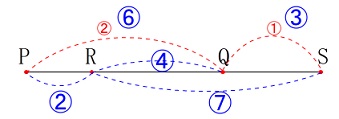（比の和の最小公倍数\(\,\color{blue}{⑨}\,\)を使っています。）

　\(\begin{eqnarray}\displaystyle
\mathrm{△BRP}&=&\frac{\mathrm{PR}}{\mathrm{PR+RQ}}\times \frac{2}{9}\times \mathrm{△ABC}\\
&=&\frac{\color{blue}{2}}{\color{blue}{2}+\color{blue}{4}}\times \frac{2}{9}\times \mathrm{△ABC}\\
&=&\frac{1}{3}\times \frac{2}{9}\times \mathrm{△ABC}\\
&=&\underline{　\frac{2}{27}　}\times \mathrm{△ABC}
\end{eqnarray}\)

こちらで進めた人は途中で「\(\,\mathrm{AR:RB}\,\)を出した方が早いかも」
と思ったかもしれませんがここまできたら突っ走っても良いですよ。
あれこれ迷っていると時間が無駄に過ぎていきます。
ここまでの方針が立つ会員は特にです。
解法をいくつも立てたからといって得点を増やしてはくれません。
レポート読み込んでいれば余裕でしょ？

\(\color{black}{\fbox{4}}\)は以上です。

\(\color{black}{\fbox{5}}\)は空間図形です。
空間での動点問題なのでとりつきにくいかもしれませんが、
平面も空間もやることは変わりません。

⇒　2022年度東京都立高校入試前期の数学第5問の問題と解説

\(\color{black}{\fbox{3}}\)は関数でした。

⇒　2022年度東京都立高校入試前期の数学【第3問】の問題と解説

後半は問題別に解説しているので最初から見通して
目標点数を決めているなら全体の配点から対策すると良いですよ。

⇒　東京都公立高校入試数学の過去問と解答解説

東京都立入試数学の問題と解説の数年分のまとめになっています。