2022年度東京都立高校入試前期の数学第5問の問題と解説

2022年(令和4年)度東京都公立高校入試問題【前期】の数学第５問の問題と解説です。
第５問は空間図形の問題です。
動点があるので関数がらみに見えますが、条件によって固定されています。
ただ、体積の求め方は見方によって難しくなります。

前半部分は下部にリンクさせてあります。

2022年(令和4年)度東京都公立高校入試問題前期の数学第５問の問題

問題は前半部分にもありますが、
第５問分だけを再度載せておきます。

\(\color{black}{\fbox{5}}\)の問題　⇒　2022年(令和4年)度東京都公立高校入試【前期】の数学第５問の問題PDF

表紙の注意書きおよびマークシートは添付していません。

2022年(令和4年)度東京都公立高校入試【前期】の数学第５問の解説

\(\color{black}{\fbox{5}}\)の空間図形問題の解説です。

動点問題に見えたので関数と融合された問題かな？
と思えたのですが、実は定点だけを扱う空間図形でした。
ただし、安易に取りくめるほど簡単でもありませんので、
空間図形への取り組み方は変えないようにしましょう。

条件が多いので問題文でも端的にまとめられています。
こういった数学らしい問題への取り組み方は、
手を止めないことです。

問題できれいにまとめてありますがここでも条件をまとめておきます。
（問題の条件は読み取れるように必ずみておきましょう。）
記号の位置は問題の図１の通りです。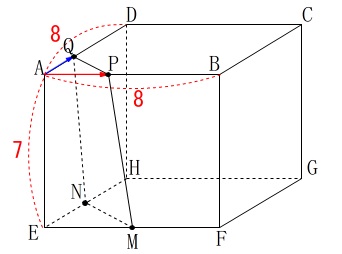条件
　直方体があり\(\,7\,,\,8\,,\,8\,\)が３辺の長さ。
　点\(\,\mathrm{M\,,\,N}\,\)はそれぞれ\(\,\mathrm{EF\,,\,EH}\,\)の中点。
　点\(\,\mathrm{P}\,\)は\(\,\mathrm{A \rightarrow B \rightarrow C}\,\)と毎秒\(\,1\,\)で移動。
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{A \rightarrow D \rightarrow C}\,\)と毎秒\(\,1\,\)で移動。
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。

〔問１〕四角形の周の長さを求める問題

〔問１〕
点\(\,\mathrm{P}\,\)が動き出して３秒後の四角形\(\,\mathrm{MPQN}\,\)の周の長さです。

\(\,\mathrm{M\,,\,N}\,\)は固定された点なので
点\(\,\mathrm{P\,,\,Q}\,\)の位置を固定します。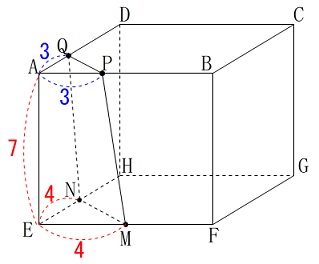素直に\(\,4\,\)辺の長さを求めに行きましょう。

四角形\(\,\mathrm{MPQN}\,\)は台形です。
　\(\hspace{10pt}\mathrm{PM=QN}\)
となるので\(\,\mathrm{PQ\,,\,PM\,,\,MN}\,\)を求めます。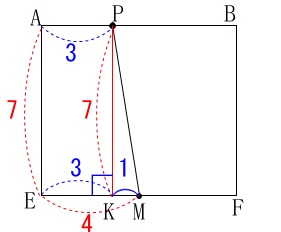\(\,\mathrm{P}\,\)から\(\,\mathrm{EF}\,\)に垂線\(\,\mathrm{PK}\,\)を引くと
直角三角形ができるので三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{PM}^2&=&\mathrm{PK^2+KM^2}\\
&=&7^2+1^2\\
&=&50\\
\mathrm{PM}&=&\pm 5\sqrt{2}
\end{eqnarray}\)
\(\,\mathrm{PM}\,\)は長さなので\(\,\mathrm{PM\,＞\,0}\,\)だから
　\(\hspace{4pt}\color{red}{\mathrm{PM=QN}=5\sqrt{2}}\)

また\(\,\mathrm{△APQ}\,\)と\(\,\mathrm{△EMN}\,\)は直角二等辺三角形です。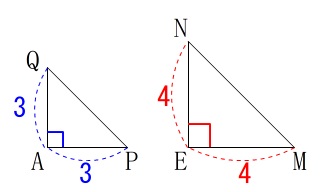三角定規になるので
（三平方の定理ですが三角定規の辺の比は覚えているでしょう。）
　\(\hspace{10pt}\color{blue}{\mathrm{PQ}=3\sqrt{2}}\)
　\(\hspace{10pt}\color{magenta}{\mathrm{MN}=4\sqrt{2}}\)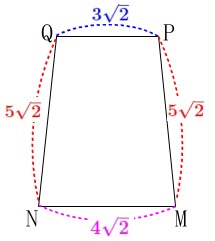よって、求める四角形\(\,\mathrm{MPQN}\,\)の周の長さは
　\(\hspace{10pt}\mathrm{\color{red}{PM}+\color{red}{QN}+\color{blue}{PQ}+\color{magenta}{MN}}\\
=\color{red}{5\sqrt{2}}+\color{red}{5\sqrt{2}}+\color{blue}{3\sqrt{2}}+\color{magenta}{4\sqrt{2}}\\
=\underline{　\color{black}{\fbox{17}}\sqrt{\color{black}{\fbox{2}}}　}　(\,\mathrm{cm}\,)\)

〔問２〕立体の体積を求める問題

〔問２〕
\(\,\mathrm{P\,,\,Q}\,\)が動き出して１２秒後の
立体\(\,\mathrm{A-MPQN}\,\)の体積を求めます。

点\(\,\mathrm{P\,,\,Q}\,\)は１２秒後に止まるので位置を確認して図形を固定しましょう。
直方体から部分的に引いていく事も考えられますが、
（手順が多くなりそうです。笑）
すい体の体積を求める公式が使えるので
公式を利用する方向で進めます。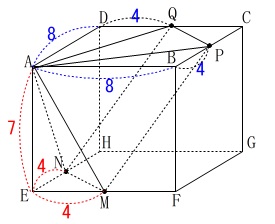立体\(\,\mathrm{A-MPQN}\,\)は四角すいで
頂点を\(\,\mathrm{A}\,\)として底面\(\,\mathrm{MPQN}\,\)は長方形です。
（正四角すいではありません。）
真上から見ると\(\,\mathrm{MPQN}\,\)が長方形だということは分かりやすいです。
ただし、図では正方形に見えますが傾いているので長方形ですよ。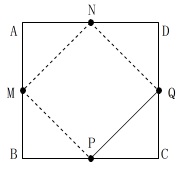
立体\(\,\mathrm{A-MPQN}\,\)を抜き出します。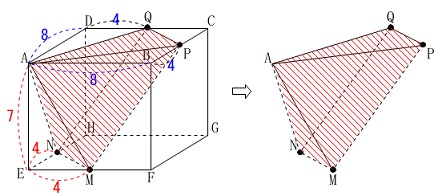三平方の定理から
　\(\hspace{10pt}\mathrm{\color{blue}{MN}=\color{blue}{PQ}}=\color{blue}{4\sqrt{2}}\)
　\(\hspace{10pt}\mathrm{\color{red}{PM}=\color{red}{QN}}=\color{red}{9}\)
　\(\hspace{10pt}\mathrm{AP=AQ}=\sqrt{80}=4\sqrt{5}\)
　\(\hspace{10pt}\mathrm{AM=AN}=\sqrt{65}\)
となります。
比較（正四角すいでは無いことの確認）のために体積には関係ない長さも出しています。
※
この問題を解きにいっている人は三平方の定理は使えるとしました。
捨てるほどでもないので『覚え太郎』シリーズで基礎固めはしておきましょう。

〔問２〕四角すいの体積を公式から求める

四角すいなので底面積と高さを求めて体積を出します。
高さを求めるところは空間での基本になるのでみておきましょう。
※
この問題の体積だけを求めるならこちらは効率悪いです。
しかし、問題が「四角すいの高さを求めよ。」まで対応できるようにしておきます。

底面積\(\,\mathrm{MPQN}\,\)から出します。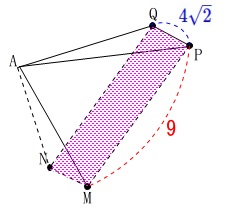　\(\hspace{10pt}\mathrm{\color{blue}{MN}=\color{blue}{PQ}}=\color{blue}{4\sqrt{2}}\)
　\(\hspace{10pt}\mathrm{\color{red}{PM}=\color{red}{QN}}=\color{red}{9}\)
から底面積\(\,S\,\)は
　\(\hspace{10pt}S=9\times 4\sqrt{2}=\color{magenta}{36\sqrt{2}}\)
（計算は後で約分しても良いです。）

高さですが、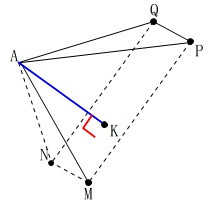頂点\(\,\mathrm{A}\,\)から面\(\,\mathrm{MPQN}\,\)へ垂線\(\,\mathrm{AK}\,\)とします。

このとき\(\,\mathrm{K}\,\)は面\(\,\mathrm{AEGC}\,\)にあります。
もっといえば\(\,\mathrm{PQ}\,\)の中点と\(\,\mathrm{MN}\,\)の中点を結んだ線分上にあります。
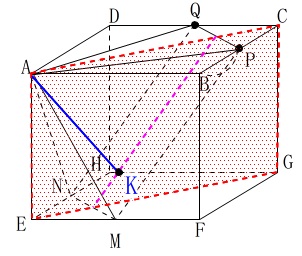真上から見るとわかりやすいですよ。

そこで面\(\,\mathrm{AEGC}\,\)を抜き出します。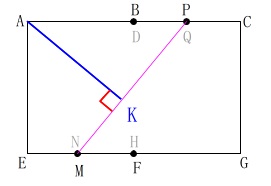このままでは線分の長さを誤解するので
\(\,\mathrm{PQ}\,\)と\(\,\mathrm{AC}\,\)との交点を\(\,\mathrm{R}\,\)、
\(\,\mathrm{MN}\,\)と\(\,\mathrm{EG}\,\)の交点を\(\,\mathrm{T}\,\)としておきます。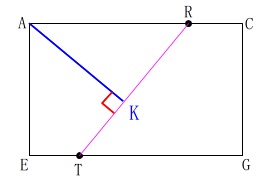
後はあれこれ分かる部分の長さを出すと
　\(\hspace{10pt}\mathrm{AC}=8\sqrt{2}\,,\,\mathrm{AE}=\color{red}{7}\)
　\(\hspace{10pt}\mathrm{AR}=\color{red}{6\sqrt{2}}\,,\,\mathrm{RT}=\mathrm{PM}=\color{red}{9}\)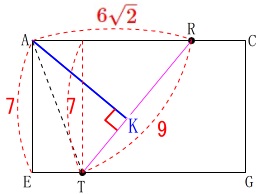ここで\(\,\mathrm{△ATR}\,\)の面積は一定なので
（底辺と高さを別にみても面積は変わらない。）
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \mathrm{AR}\times \mathrm{AE}&=&\frac{1}{2}\times \mathrm{RT}\times \mathrm{\color{blue}{AK}}\\
6\sqrt{2}\times 7&=&9\times \mathrm{AK}\\
\mathrm{\color{blue}{AK}}&=&\color{blue}{\frac{14\sqrt{2}}{3}}
\end{eqnarray}\)
底面積\(\,S\,\)は
　\(\hspace{10pt}S=\color{magenta}{36\sqrt{2}}\)
だったので（最初に出しています。）求める立体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times S\times \mathrm{AK}\\
&=&\frac{1}{3}\times 36\sqrt{2}\times \frac{14\sqrt{2}}{3}\\
&=&\underline{　\color{black}{\fbox{　112　}}　}　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

ちょっと説明を省いたところもありますが、
会員にはくどい説明になったでしょうね。

三角形や立体の高さを求めるときの
「見方をかえる」ための説明でした。

次の解き方がこの問題では早いです。
もちろん、四角すいとしての高さを求める方針で進めたなら突っ走って良いですよ。

〔問２〕四角すいの体積を２つに分ける別解

今度は対称性から四角すいの体積を
2つの三角すいとみて体積を出します。ここで対称性をみてください。
頂点\(\,\mathrm{A}\,\)を通り、
底面\(\,\mathrm{MPQN}\,\)の対角線を含む面で切り分けます。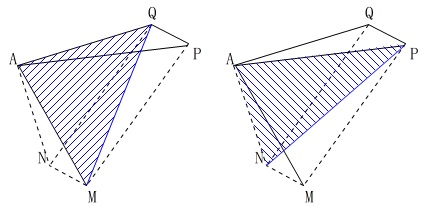（対角線はどちらでも良いですよ。）
どちらも同じ大きさの（合同な）三角すいなので
求める体積は\(\,\mathrm{△APQ}\,\)を底面とし
高さを\(\,\mathrm{AE}\,\)とする三角すい２つ分です。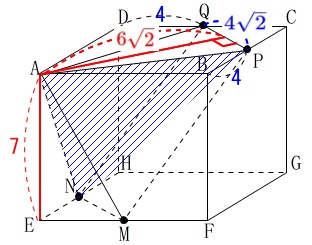ここからは一気に答えにいけます。

底面とみる\(\,\mathrm{△APQ}\,\)において
　底辺は\(\hspace{10pt}\mathrm{PQ}=\color{blue}{4\sqrt{2}}\)
　高さは\(\hspace{10pt}\color{red}{6\sqrt{2}}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times \color{blue}{4\sqrt{2}}\times \color{red}{6\sqrt{2}}\\
&=&\color{magenta}{24}
\end{eqnarray}\)
１つの三角すい\(\,\mathrm{A-NPQ}\,\)の体積\(\,V_1\,\)は
高さが\(\,\mathrm{AE}=\color{red}{7}\,\)なので
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \color{magenta}{24}\times \color{red}{7}\\
&=&56
\end{eqnarray}\)
求める四角すいの体積\(\,V\,\)は\(\,V_1\,\)が２つ分なので
　\(\begin{eqnarray}\displaystyle
V&=&V_1\times 2\\
&=&56\times 2\\
&=&\underline{　\color{black}{\fbox{　112　}}　}　(\mathrm{cm^3})
\end{eqnarray}\)

それぞれの長さが出せない場合は先の解説を見直してください。
\(\,\mathrm{△APQ}\,\)の底辺や高さは面\(\,\mathrm{ABCD}\,\)を抜き出すことですぐに求まります。

立体が斜めを向いているからわかりにくいですが、
長方形\(\,\mathrm{MPQN}\,\)をぺたんと下にすれば対称性に気がつくでしょう。

四角すいとみても公式が使えますが
体積や面積を求める場合に
　「全体－部分」
　「部分＋部分」
という練習をしてきた人なら計算は圧倒的にこちらが楽です。

どちらでも良いです。
この問題に来る前に基本問題を短時間で終わらせ、
少し時間に余裕を持たせておくと見方を変えて取り組むこともできますね。

以上です。

最初から通してみてみると問題のバランスが見えてきますよ。

⇒　2022年(令和4年)度東京都公立高校入試問題【前期】の数学の問題と解説

\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)の解説です。
後半はそれぞれの問題を別々に解説しています。

⇒　東京都公立高校入試数学の過去問と解答解説

過去数年分の都立入試の解説がありますので
年度別、問題別にみておきたい場合はご利用ください。