2022年度東京都立高校入試前期の数学【第3問】の問題と解説

2022年(令和4年)度東京都公立高校入試問題【前期】の数学第３問の問題と解説です。
第３問は関数総合問題となりますので差がつきやすいですが
基本をおさえておけば得点し難い訳ではありません。
〔問３〕ではいろいろな設定ができますので１つの解答例としてみて下さい。

前半部分は下部にリンクさせてありますので、
もう一度全体を通してみて見直しておくと良いでしょう。

2022年(令和4年)度東京都公立高校入試問題前期の数学第３問の問題

問題は前半部分にもありますが再度載せておきます。

　⇒　2022年(令和4年)度東京都公立高校入試【前期】の数学第3問の問題PDF

表紙の注意書きおよびマークシートは添付していません。

2022年(令和4年)度東京都公立高校入試【前期】の数学第3問の解説

\(\color{black}{\fbox{3}}\)は関数総合問題の解説です。
変域、直線の式を求める基本問題と座標を文字設定する応用問題があります。

　曲線\(\,\ell\,\)：\(\displaystyle y=\frac{1}{4}\,x^2\,\)
　\(\,\ell\,\)上の点である\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-8\,\)
これが問題全体に与えられた共通の条件です。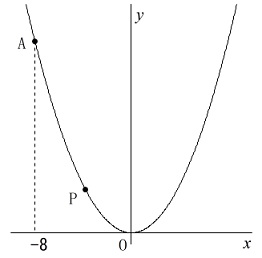点\(\,\mathrm{P}\,\)について\(\,x\,\)座標が\(\,-8\,\)より大きい、
ということが書かれています。
こういった条件は後で必ずと言って良いほど使いますので
見逃さないようにしましょう。

〔問１〕変域を求めるときの注意点

文字が\(\,a\,,\,b\,\)となっていますが\(\,x\,,\,y\,\)の変域です。
\(\,a\,\)が（\(\,x\,\)の変域が）
　\(\hspace{4pt}-4\,≦\,a\,≦\,1\)
のときの\(\,b\,\)の変域（\(\,y\,\)の変域）です。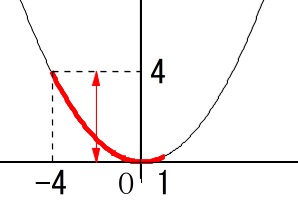　\(\hspace{10pt}\underline{　\color{black}{\fbox{0}}\,≦\,b\,≦\color{black}{\fbox{4}}　}\)

\(\,y\,\)の変域に\(\,x=1\,\)の値は関係しませんので注意しましょう。
数値だけ見ててもミスし易いのでグラフに書き込んで確認すると良いですよ。

〔問２〕直線の式の求め方

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,2\,\)のとき\(\displaystyle y=\frac{1}{4}\,x^2\,\)から
　\(\hspace{10pt}\mathrm{P}\,(\,2\,,\,1\,)\,\)
となるので２点
　\(\,\mathrm{A\,(\,-8\,,\,16\,)}\,\)
　\(\,\mathrm{P\,(\,2\,,\,1\,)}\,\)
を通る直線を求めることになります。

求める直線を\(\,y=\color{red}{a}x+\color{blue}{b}\,\)とします。
　\(\hspace{10pt}\displaystyle (傾き)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)
なので
　\(\displaystyle \color{red}{a}=\frac{16-1}{-8-(2)}=\frac{15}{-10}=-\frac{3}{2}\)
※
計算途中の\(\,=\,\)は縦につなげる事をおすすめしていますが、
分母、分子を同時にする場合は横にすることが多いです。
自分でやる場合は分母と分子の増加量は別に計算しています。

傾きが求まりましたので直線の式を書き直します。
　\(\hspace{10pt}\displaystyle y=-\frac{3}{2}\,x+\color{blue}{b}　･･･①\)

次は切片（\(\,y\,\)切片）\(\,\color{blue}{b}\,\)です。
これは直線が通る点をどちらでも1つ代入すれば求まります。
　\(\,\mathrm{P\,(\,2\,,\,1\,)}\,\)
を\(\,①\,\)に代入します。
　\(\begin{eqnarray}\displaystyle
1&=&-\frac{3}{2}\times (2)+\color{blue}{b}\\
\color{blue}{b}&=&4
\end{eqnarray}\)
よって求める直線は
　\(\hspace{10pt}\displaystyle \underline{　y=-\frac{3}{2}\,x+4　}\)
　
代入する点を\(\,\mathrm{A\,(\,-8\,,\,16\,)}\,\)にして同じになるか確認してみてください。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

２点を通る直線の式を求める方法は
連立方程式でも良いですが傾き（または切片）から求める方が早いです。

　\(\hspace{10pt}\displaystyle \underline{　y=\color{black}{\fbox{\(\displaystyle \,-\frac{3}{2}\,\)}}\,x+\color{black}{\fbox{4}}　}\,\)
記号を選ぶので間違えないように気をつけましょう。
ケアレスミスは悔しいです。（笑）

〔問３〕座標を文字で設定する

条件を満たす点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。
条件　
　・点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,0\,\)より大きく\(\,8\,\)より小さい。
　・点\(\,\mathrm{Q}\,\)は点\(\,\mathrm{A}\,\)を通り\(\,y\,\)軸に平行な直線と、点\(\,\mathrm{P}\,\)を通り\(\,x\,\)軸に平行な直線との交点。
　・点\(\,\mathrm{R}\,\)は直線\(\,\mathrm{PQ}\,\)と線分\(\,\mathrm{AO}\,\)との交点。
　・\(\,\mathrm{PR:RQ=3:1}\,\)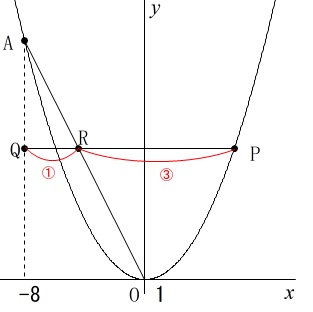おおよそは問題の図の通りです。
この問題に不要な条件、足りない条件はありませんので
条件を読みとれるかがこの問題の課題の１つです。

文字を使っての点の設定ですが
点\(\,\mathrm{P}\,\)か、点\(\,\mathrm{R}\,\)を文字で表すか２つに分かれたと思います。
どちらでも良いですが直接答えになる点\(\,\mathrm{P}\,\)を文字で表しておきます。

点\(\,\mathrm{P}\,\)は\(\,\ell\,\)上の点なので\(\,x\,\)座標を\(\,t\,\)とすると、
（文字は何でも良いですよ。）
　\(\hspace{10pt}\displaystyle \mathrm{P}\,\left(\,\color{red}{t}\,,\,\frac{1}{4}\,t^2\,\right)\)
点\(\,\mathrm{Q}\,\)は点\(\,\mathrm{P}\,\)と\(\,y\,\)座標が同じで\(\,x=-8\,\)なので
　\(\hspace{10pt}\displaystyle \mathrm{Q}\,\left(\,-8\,,\,\frac{1}{4}\,t^2\,\right)\)

直線\(\,\mathrm{AO}\,\)は原点\(\,(\,0\,,\,0\,)\)と点\(\,\mathrm{A}\,(\,-8\,,\,16\,)\)を通るので
　\(\hspace{10pt}y=-2x\)

点\(\,\mathrm{R}\,\)は直線\(\,\mathrm{AO}\,\)と\(\,\mathrm{PQ}\,\)との交点ので\(\,y\,\)座標が同じだから\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle
\frac{1}{4}\,t^2&=&-2\,x\\
x&=&-\frac{1}{8}\,t^2
\end{eqnarray}\)
これから点\(\,\mathrm{R}\,\)の座標は
　\(\hspace{10pt}\displaystyle \mathrm{R}\,\left(\,\color{blue}{-\frac{1}{8}\,t^2}\,,\,\frac{1}{4}\,t^2\,\right)\)

\(\,\mathrm{P\,,\,Q\,,\,R}\,\)の\(\,y\,\)座標は同じなので\(\,x\,\)座標だけを図に書き込みます。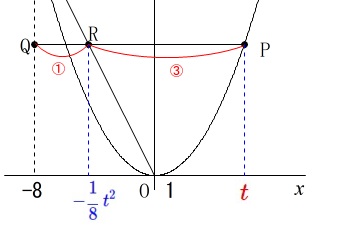一気に比例式を立ててもいいですが、
線分の長さを表しておきますね。
　\(\begin{eqnarray}
\mathrm{PR}&=&\color{red}{t}-\left(\color{blue}{-\frac{1}{8}t^2}\right)\\
&=&t+\frac{1}{8}\,t^2
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\mathrm{RQ}&=&\left\{\color{blue}{-\frac{1}{8}t^2}-(-8)\right\}\\
&=&-\frac{1}{8}\,t^2+8
\end{eqnarray}\)
※
長さ（正の値）なので大きい方から小さい方を引いています。

これらから条件をみたす\(\,t\,\)を求めると
　\(\begin{eqnarray}\displaystyle
\mathrm{PR:RQ}&=&3:1\\
\left(t+\frac{1}{8}\,t^2\right):\left(-\frac{1}{8}\,t^2+8\right)&=&3:1\\
3\left(-\frac{1}{8}\,t^2+8\right)&=&t+\frac{1}{8}\,t^2
\end{eqnarray}\)
これを解くと
　\(\hspace{10pt}t=-8\,,\,6\)
（計算力も問われていますので２次方程式は自分で解いてください。）
条件に適している方が答えになります。
　\(\hspace{10pt} t=\underline{　6　}\)

点\(\,\mathrm{R}\,\)を\(\,(\,t\,,\,-2t\,)\,\)とおいても同じ答えが出ます。
ただし、少し遠回りになりそうです。

図形的にみると
　\(\,\mathrm{PR:RQ=3:1}\,\)
なので\(\,\mathrm{AO}\,\)を延長してみたくなります。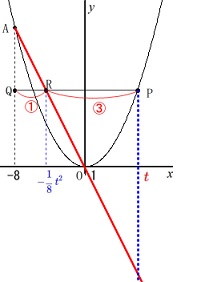ただ、
問題用紙からは想定していないようなので省略します。笑