2022年(令和4年)度北海道公立高校入試問題の数学の問題と解説

2022年(令和4年)度北海道公立高校入試問題の数学の問題と解説です。
この年度から学校裁量問題が無くなるなどのいくつか変更がありました。
数学問題の全体の構成としてはそれほど変わりありませんが、
目標点数に応じた対策は必要になりますので注意しましょう。

2022年(令和4年)度北海道公立高校入試問題の数学問題

令和４年度北海道立高校入試の数学問題です。

⇒　2022年(令和4年)度北海道公立高校入試問題の数学の問題

事前に北海道の教育委員会から（数学に関して）
・学校裁量問題・標準問題の区別は無くなりすべての学校で同一問題となる。
・一般選抜の学力検査が１００点、５０分となる。
（６０点、４５分が前年度まで）
と通知されていました。
募集要項などには必ず目を通しておきましょう。

2022年(令和4年)度北海道公立高校入試問題の数学の解説

変更点については先に書いておきましたが、
ここで気をつけておきたいのは試験時間の変更です。
試験時間が延長されるところに注意が必要ですね。
「たった５分だからそれほど変わらない？」
と考えた人は苦戦したかもしれません。

配点も変更され問題数は若干増えた？
という感じはしますが配点比率の問題なのであまり気にしなくて良いです。
まあ、ここは対策ページではありませんので深くは述べません。

対策は塾や家庭教師の先生に聞いて下さい。
会員はお気軽にお問合せ下さい。
ここでは、
「過去問で傾向を知るなら裁量問題にも目を通しておくこと。」
とだけ言っておきます。

解説の中である程度見えてくると思うので先に進みます。

問題は大問\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まであります。
問題数としては増えていませんね。
試験時間の延長の影響はここではありません。
（当会独自の見解なので気にしないで下さい。）

第１問小問集合

\(\color{black}{\fbox{1}}\)
計算問題を含めた\(\,8\,\)問の小問集合です。

問１
(1)
　\(\hspace{10pt}8\times (-4)\\
=\underline{　-32　}\)
符号に注意すれば問題ないでしょう。

(2)
　\(\hspace{10pt}(-5)^2-9\div 3\\
=25-3\\
=\underline{　22　}\)
計算順序を問われています。
\(\hspace{4pt}(-5)^2=25\,,\,-(5)^2=-25\)
の違いと、どこで計算が途切れるか分かっていれば良いです。

(3)
　\(\hspace{10pt}4\sqrt{5}+\color{red}{\sqrt{20}}\\
=4\sqrt{5}+\color{red}{2\sqrt{5}}\\
=\underline{　6\sqrt{5}　}\)
素因数分解して
\(\hspace{4pt}\sqrt{20}=2\sqrt{5}\,\)
の部分はていねいにやった方が良いです。

問２
代入問題です。
　\(\hspace{10pt}a^2+2ab\\
=a(a+2b)\\
=7\{7+2\times (-3)\}\\
=7(7-6)\\
=\underline{　7　}\)
（３行目は暗算でも良いです。）
この程度なら直接代入しても良いですが、
　\(\hspace{10pt}a^2+ab\\
=7^2+2\times 7\times (-3)\\
=49-42\\
=\underline{　7　}\)
（ややこしい代入問題に対応できるように）
与式（求値式）をある程度変形して
最後に代入すると楽なことが多いです。

問３
座標を求めます。

直線\(\,y=-2x+8\,\)と\(\,x\,\)軸との交点ですが、
\(\,x\,\)軸は\(\,y=0と\,\)いう直線になります。
　\(\begin{eqnarray}\displaystyle
-2x+8&=&0\\
-2x&=&-8\\
x&=&4
\end{eqnarray}\)
答え　\(\hspace{4pt}\underline{　\mathrm{A}\,(\,4\,,\,0\,)　}\)

「交点」を求めるときは連立方程式ですよ。

この問題は\(\,x\,\)座標だけを求める問題ではありません。
「座標を求めなさい。」のときは、
\(\,x\,,\,y\,\)座標の両方を答えに書くことを忘れないようにしましょう。

問４
連立方程式です。
　\( \begin{cases}
\hspace{4pt} 3x-2y=5　･･･①\\
\hspace{4pt} -x+4y=5　･･･②
\end{cases}\)

ここでは\(\,y\,\)を消去し\(\,x\,\)を先に求めます。
　\(\hspace{26pt}6x-4y=10\\
\underline{+)　-x+4y=5　}\\
\hspace{26pt}5x\hspace{23pt}=15\\
\hspace{54pt}x=3\)
このとき\(\,①\,\)から
　\(\begin{eqnarray}\displaystyle
3\times (3)-2y&=&5\\
9-2y&=&5\\
-2y&=&-4\\
y&=&2
\end{eqnarray}\)
\(\,②\,\)に\(\,x=3\,\)を代入しても同じです。
　\(\hspace{10pt}\underline{　x=3\,,\,y=2　}\)

連立方程式を解くときの基本は一文字消去です。

問５
不等式の表し方です。
「以下」は等号をつけます。

　\(\hspace{10pt}\underline{\underline{　x\,≦\,10　}}\)

解説とは関係ないですけど、
最近飛行機に乗ってない、という人多くないですか？
問題みて旅したい欲求が増してしまいました。

問６
作図です。

線分\(\,\mathrm{AC}\,\)上に\(\,\mathrm{AP:PC=3:1}\,\)となる点\(\,\mathrm{P}\,\)を作図します。
点\(\,\mathrm{E}\,\)は中点連結定理から\(\,\mathrm{AC}\,\)の中点なので、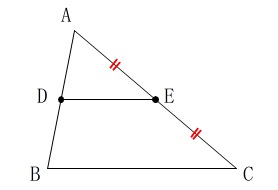
線分\(\,\mathrm{EC}\,\)の中点を作図することになります。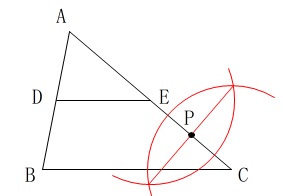線分\(\,\mathrm{EC}\,\)の垂直二等分線と
線分\(\,\mathrm{AC}\,\)の交点が\(\,\mathrm{P}\,\)です。

この問題はヒントになる\(\,\mathrm{DE}\,\)がなくても、
当会の作図問題集『さくっと！』の問題番号２１そのものです。
会員は確認しておきましょう。

第２問データの活用（箱ひげ図）

\(\color{black}{\fbox{2}}\)
データの活用における箱ひげ図の問題です。
移行措置期間なので前倒しの出題になりますが、
来年以降本格的に出てくるでしょう。

問１
箱ひげ図と『四分位数』の基本確認問題です。
(1)
\(\,\mathrm{B}\,\)組の第３四分位数を求めます。用語の確認です。
　\(\hspace{10pt}\underline{　8.6　(秒)}\)

箱ひげ図はかけるようになれば自ずと意味が理解できます。

(2)
データの散らばり（分布）についての問題です。

ア：「範囲」は最大値と最小値の差です。
　\(\,\mathrm{A}\,\)組：\(\hspace{4pt}10.3-6.2=4.1\)
　\(\,\mathrm{B}\,\)組：\(\hspace{4pt}10.5-6.5=4.0\)
\(\,\mathrm{A}\,\)組の方が大きい。×
イ：「四分位範囲」は第３四分位数と第１四分位数との差です。
　\(\,\mathrm{A}\,\)組：\(\hspace{4pt}8.7-7.3=1.4\)
　\(\,\mathrm{B}\,\)組：\(\hspace{4pt}8.6-7.4=1.2\)
\(\,\mathrm{A}\,\)組の方が大きい。○
ウ：「平均値」は箱ひげ図からは分かりません。×
※
箱ひげ図でも平均値を示すこともありますが、
ここではありません。
エ：「最大値」は
　\(\,\mathrm{A}\,\)組：\(\hspace{4pt}10.3\)
　\(\,\mathrm{B}\,\)組：\(\hspace{4pt}10.5\)
\(\,\mathrm{B}\,\)組の方が大きい。×

適当なものは\(\,\underline{　イ　}\,\)だけです。
　
おかしな事に代表値（平均値、中央値、最頻値）が小学校の内容になったので
今後が箱ひげ図だけの出題だとは考えにくいのですが、
データの活用では用語の意味を確認しておきましょう。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

箱ひげ図を攻略するには代表値抜きでは難しいですよ。
特に中央値を知らなければ箱ひげ図の意味が分かりません。

問２
この問題も箱ひげ図からの読み取りです。

箱ひげ図は最大値最小値と四分位数を
箱とひげで表したものなので代表値は読み取れません。
（中央値は第２四分位数なので分かります。）

それを話し合っているようです。
登場人物は３人いますがどうでも良いです。
要は、\(\,\mathrm{A}\,\)組、\(\,\mathrm{B}\,\)組に\(\,7.5\,\)秒より早い人はどれだけいるか、考えます。
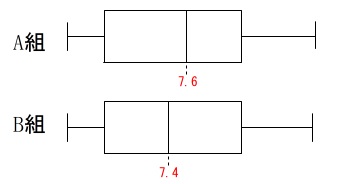中央値：\(\,\mathrm{A}\,\)組\(\,7.6\,\)秒、\(\,\mathrm{B}\,\)組\(\,7.4\,\)秒
は箱ひげ図から読み取れます。

\(\,15\,\)人のデータなので中央値は\(\,8\,\)人目と考えられます。
（\(\,8\,\)人目だけとは限りません。）

「より速い人」は数値の小さい方であることに注意して、
色々とデータを設定すれば見えてきますが簡単に済ませます。

\(\,\mathrm{B}\,\)組では\(\,8\,\)人目が\(\,7.4\,\)秒なので、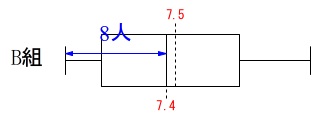
\(\,7.5\,\)秒より速い人は少なくとも\(\color{black}{\fbox{　8　}}\)人はいます。
記録が\(\,7.5\,\)秒以上の人が\(\,8\,\)人いた場合は中央値が\(\,7.5\,\)以上になるからです。

箱ひげ図での注意点は学校でもやっているでしょうから次行きます。

\(\,\mathrm{A}\,\)組では\(\,8\,\)人目が\(\,7.6\,\)秒なので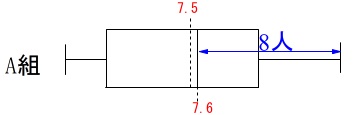
\(\,7.5\,\)秒より速い人は多くとも\(\color{black}{\fbox{　7　}}\)人になります。

ここはすぐに出せるとは思えません。
　\(\hspace{4pt}○○○|\,8人目\,|○○○\)
中央値前後にデータを当てはめて試して確認する方が良いです。
（試験時間の延長の理由の一部はここにもあります。）

よって、\(\,7.5\,\)秒より速い人は\(\color{black}{\fbox{　\(\,\mathrm{B}\,組\,\)　}}\)の方が多い。

このことは言えますが箱ひげ図で分かることは限られますね。
代表値の意味が分かっていないと箱ひげ図の意味はとれませんので、
小学校の算数でがんばって下さい。笑

第３問関数

\(\color{black}{\fbox{3}}\)
関数の問題です。
２次関数の比例定数を求める基本問題と
文字設定して方程式を解く裁量問題風の問題があります。

問題全体にある条件はシンプルで
　関数\(\,y=ax^2\hspace{4pt}(\,a\,は正の定数)　･･･①\,\)
　\(\,①\,\)上の点\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,t\,(\,t\,＞\,0\,)\)とする。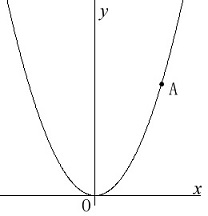問題に与えられたグラフから位置関係が確認できます。

問１
比例定数を求めます。
ただし、全体に通して言えることではありません。
この問に限った比例定数になりますので注意しておきましょう。

点\(\,\mathrm{A}\,\)の座標が\(\,(\,\color{red}{2}\,,\,\color{blue}{12}\,)\,\)のときの\(\,a\,\)です。
点\(\,\mathrm{A}\,\)は\(\,①\,\)上の点ので\(\,y=ax^2\,\)に代入して
　\(\begin{eqnarray}\displaystyle
\color{blue}{12}&=&a\times (\,\color{red}{2}\,)^2\\
a&=&\underline{　3　}
\end{eqnarray}\)

問２
比例定数と関数上の点の\(\,x\,\)座標とにおける関係を考えます。

コンピューターを使っても手書きでやっても関係は変わりませんが、
ここではコンピューターの代わりを自分でやれ、ということです。

条件（問題を簡単に書き換えると）
　点\(\,\mathrm{A}\,\)を通る\(\,x\,\)軸に平行な直線を引く。
　\(\,①\,\)との交点を\(\,\mathrm{B}\,\)とする。（\(\,\mathrm{A}\,\)と異なる点。）
　\(\,\mathrm{∠AOB=90^{\circ}}\,\)
「このとき次の問に答えよ。」です。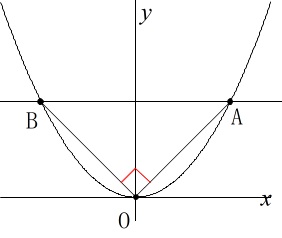

(1)
文字設定に慣れている人は(2)が先に出てもおかしくない問題ですが、
問題の中にヒントがあります。
「\(\,a\,\)の値をいくつか決めて、・・・」
つまり、いくつか自分で試しにやって下さい、ということです。
数学問題を解くときの基本ですね。

ただし、
\(\,\mathrm{∠AOB=90^{\circ}}\,\)を満たすのはどういうときかは考えなければなりません。

直径\(\,\mathrm{AB}\,\)の円？
いやいや、\(\,y\,\)軸で左右対称だから、
見た目からも直角二等辺三角形でしょう。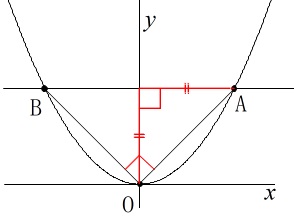この関係を満たすように試していきます。
※
条件を満たすのは直径\(\,\mathrm{AB}\,\)として原点を通る円ですが、
結局は直角二等辺三角形に行き着きます。

\(\,a=1\,\)のとき\(\,\mathrm{A}\,\color{blue}{(\,t\,,\,t^2\,)}\,\)
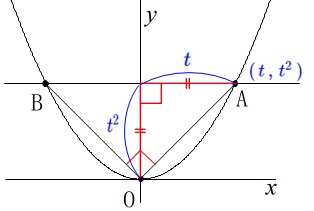このとき
　\(\begin{eqnarray}\displaystyle
t^2&=&t\\
t^2-t&=&0\\
t(t-1)&=&0\\
t&=&0\,,\,1
\end{eqnarray}\)
\(\,t\,＞\,0\,\)なので\(\,t=1\,\)
これを\(\,a=1\,,\,2\,,\,\cdots\,\)と続けると
　\(\begin{array}{|c|c|c|c|c|} \hline
a & 1 & 2 & 3 & \cdots \\ \hline
t & 1 & \displaystyle \color{red}{\frac{1}{2}} & \displaystyle \frac{1}{3} & \cdots \\ \hline
\end{array}\)
となるので表の\(\,\mathrm{X=\displaystyle \underline{　\frac{1}{2}　}}\,\)で、
\(\,a\,\)と\(\,t\,\)のかけたもの、
つまり「\(\,\underline{　積　}\,\)」が一定で\(\,\underline{　1　}\,\)あることが予想されます。

この予想が成り立つことを説明するのが(2)です。

(2)
比例定数\(\,a\,\)をそのまま関係式にすれば
(1)の具体例の方程式を解いたときと同じです。

\(\,x\,\)座標が\(\,t\,\)のとき\(\,\mathrm{A}\,(\,t\,,\,a\,t^2\,)\,\)とおくと、
\(\,\mathrm{∠AOB=90°}\,\)となるのは\(\,\mathrm{△AOB}\,\)が直角二等辺三角形になるときで
\(\,\mathrm{A}\,\)の\(\,x\,\)座標と\(\,y\,\)座標が等しくなるときである。
このとき
　\(\begin{eqnarray}\displaystyle
t&=&a\,t^2\\
a\,t^2-t&=&0\\
t(a\,t-1)&=&0\\
t&=&0\,,\,a\,t=1
\end{eqnarray}\)
ここで\(\,t＞0\,\)なので
　\(\hspace{4pt}a\,t=1\)
つまり、\(\,a\,,\,t\,\)の積は一定で\(\,1\,\)となる。

(1)が無くても(2)は説明できたと思いますが、
\(\,\mathrm{∠AOB=90^{\circ}}\,\)という条件の使い方が問題ですね。

コンピューターなどの言葉は必要ありあせんが、
問題文だけ読んでいたら難しく感じたでしょう。
「いくつか決めて」というのが大きなヒントであり、ポイントです。

\(\color{black}{\fbox{3}}\)は以上です。

ここまでで配点の\(\,65\,\)％になります。
\(\color{black}{\fbox{2}}\)までを前半としても良かったのですが後半が長くなりそうだったので、
ここまでを前半としておきます。

第４問第５問（後半）

\(\color{black}{\fbox{4}}\)、\(\color{black}{\fbox{5}}\)を後半として分けて解説しておきます。
\(\color{black}{\fbox{4}}\)は平面図形で、\(\color{black}{\fbox{3}}\)と同じように予想と証明があります。
\(\color{black}{\fbox{5}}\)は平面図形と確率です。

確率の問題はシンプルではありますが、
取り組み方で差がついたのではないでしょうか。

⇒　2022年度北海道公立高校入試問題の数学の問題と解説（後半）

全体として問題数はほぼ変化無し、という感じでした。

⇒　北海道の公立高校入試数学の過去問と解説

統一問題では問題の難易度がばらつきますので、
目標点数によっては裁量問題にも目を通しておいた方が良いですね。