2022年(令和4年)度北海道公立高校入試問題の数学の問題と解説の後半です。
第４問は平面図形、第５問は平面図形と確率になります。
確率問題は基本通りできていればとりやすいですが、
取り組み方で差がついたかもしれません。
2022年(令和4年)度北海道公立高校入試問題の数学問題
令和４年度北海道立高校入試の数学問題です。
問題は前半の解説にも載せてありますのでここでは\(\color{black}{\fbox{4}}\)、\(\color{black}{\fbox{5}}\)だけを載せておきます。
2022年(令和4年)度北海道公立高校入試問題の数学の解説
北海道の方はご存じだと思いますが
学校裁量問題と標準問題の区別は無くなり同一問題になりました。
問題が統一された共通問題で気をつけたいのは、
比較的とりやすい基本問題と
取り組み方によって差が出る問題が混在するということです。
時間の延長が示すように試験中の作業量が増えるということです。
このことは他の都道府県でも言えることですので
対策するときに気をつけて取り組むと良いですよ。
第４問
\(\color{black}{\fbox{4}}\)
平面図形総合問題です。
全体に通じる条件は非常にシンプルですね。
条件
\(\,\mathrm{∠BCA=90^{\circ}}\,\)
\(\,\mathrm{∠ABC}\,\)の二等分線と\(\,\mathrm{AC}\,\)の交点が\(\,\mathrm{D}\,\)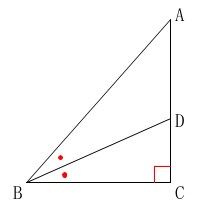
問１
角度を求めます。
図の中に分かる角度を書きこんで行けば良いだけです。
直角三角形なので
\(\,\mathrm{∠BAC=\color{red}{40^{\circ}}}\,\)のとき\(\,\mathrm{∠ABC=\color{blue}{50^{\circ}}}\,\)です。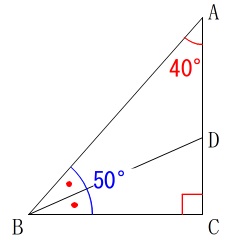
このとき\(\,\mathrm{BD}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線なので
\(\hspace{4pt}\mathrm{∠ABD=∠CBD}=\color{magenta}{25^{\circ}}\)
すべての角を書き込みますね。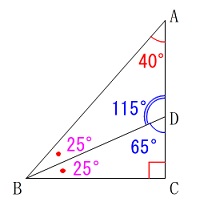
\(\hspace{10pt}\mathrm{∠ADB}=\underline{ 115^{\circ} }\)
すべての角を求める必要はありませんよ。
\(\,\mathrm{∠CBD=25^{\circ}}\,\)
が分かった時点で
\(\begin{eqnarray}\displaystyle
\mathrm{∠ADB}&=&\mathrm{∠CBD+∠BCD}\\
&=&25^{\circ}+90^{\circ}\\
&=&\underline{ 115^{\circ} }
\end{eqnarray}\)
で良いです。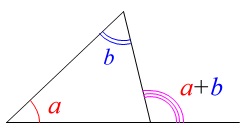
問２
４点が１つの円周上にあることの予想と証明です。
この手の問題は読み取るポイントを間違えないようにしましょう。
数学の条件を読み取るのであって。
問題の都合上名前をつけていた方が示しやすいからなので
「望さんって誰だろう？」とか余計なことは考えなくて良いです。
条件
点\(\,\mathrm{E}\,\)は\(\,\mathrm{AB}\,\)上の点で\(\,\mathrm{BC=BE}\,\)
線分\(\,\mathrm{BD}\,\)と\(\,\mathrm{CE}\,\)の交点を\(\,\mathrm{F}\,\)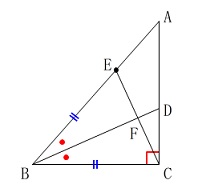
大問の最初にある条件はその問題全体に通じる条件なので忘れないように。
このとき「４点\(\,\mathrm{B\,,\,C\,,\,D\,,\,E}\,\)が１つの円周上にある」ことを証明します。
（望さんの見通し）の中で結果として証明したい
「４点\(\,\mathrm{B\,,\,C\,,\,D\,,\,E}\,\)が１つの円周上にある」
ことの代わりの証明が方針として書かれています。
どういうことかというと、
結果として証明したいことは
（望さんの見通し）が示せれば良い。
ということです。
この手順は三角形の合同や相似の証明でもいえます。
合同を示したいのであれば合同条件をそろえる。
相似を示したいのであれば相似条件をそろえる。
などのことです。
この問題は相似の証明ですが合同も同じです。
簡単にですがまとめていますので見て参考にしてください。
会員はレポートで証明の手順を確認してください。
ここでは「４点が１つの円周上にある」ことの証明なので
「何を言えば良いか？」を望さんがヒントにしてくれています。
(1)
相似を証明するのでは無く、
相似であれば円周角の定理から(2)が証明できるということです。
（望さんの見通し）をうめていきましょう。
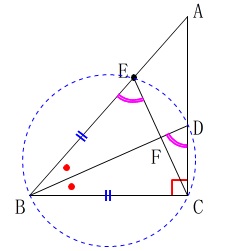見通しの中にある
\(\hspace{10pt}\mathrm{\color{magenta}{∠BEC}}=\color{magenta}{∠}\color{black}{\fbox{\( \mathrm{\color{magenta}{BDC}} \)}}\)
であれば同一の弦に対する円周角が等しくなるので
\(\hspace{10pt}\mathrm{△\color{black}{\fbox{ BEF }}}\,\)∽\(\,\mathrm{△\color{black}{\fbox{ BDC }}}\,\)
または（記号の順番を入れかえた）
\(\hspace{10pt}\mathrm{△BFE}\,\)∽\(\,\mathrm{△BCD}\,\)
が示せれば良いということです。
※
相似（合同）の場合は記号の順番をそろえることを忘れないように。
グダグダな説明が長くなったのでとっとと先に行きます。
(2)
(1)が埋まれば(2)は相似から円周角の定理につなげるだけです。
もう一度みておきます。円周上に\(\,4\,\)点\(\,\mathrm{B,C,D,E}\,\)があるなら円周角が等しくなるので、
その逆、円周角が等しくなれば証明できたことになります。
「定理の逆」が正しいからですね。
（見通し）通り相似の証明を進めて行きます。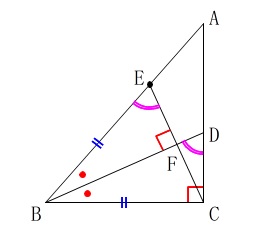
\(\,\mathrm{△BCE}\,\)が二等辺三角形であることを忘れないようにしましょう。
問題の条件にあることは必ず使います。
（たまに使わなくても良い条件はありますけど。）
（証明）
\(\,\mathrm{△BEF}\,\)と\(\,\mathrm{△BDC}\,\)において
\(\hspace{4pt}\mathrm{\color{red}{∠EBF}}=\mathrm{\color{red}{∠DBC}}\,（仮定） ･･･①\)
また\(\,\mathrm{△BCE}\,\)は\(\,\mathrm{BC=BE}\,\)の二等辺三角形で
頂角の二等分線は底辺を垂直に\(\,2\,\)等分するので
仮定の\(\,\mathrm{∠BCA=90^{\circ}}\,\)より
\(\hspace{4pt}\mathrm{\color{red}{∠BFE}=\color{red}{∠BCD}}=90^{\circ} ･･･②\)
\(\,①②\,\)から
２組の角がそれぞれ等しい。
よって
\(\,\mathrm{△BEF}\,\) ∽ \(\,\mathrm{△BDC}\,\)
このことから
\(\,\mathrm{\color{magenta}{∠BEC}=\color{magenta}{∠BDC}}\,\)
１つの弦に対する円周角が等しいので
４点\(\,\mathrm{B,C,D,E}\,\)は１つの円周上にある。（終わり）
証明の書き方はお任せします。
相似条件をそろえる順番はどうでも良いです。
手を抜いた証明よりはいいので
「これは書いた方が良いのかな？」
と不安になるようなら書いておきましょう。
⇒ 中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント
\(\color{black}{\fbox{4}}\)は以上です。
第５問
\(\color{black}{\fbox{5}}\)
問１は線分の長さと面積、問２は確率で問題が変わります。
つながりが無いので切り替えが大切です。
問１平面図形（長さと面積）
問１
ここは順に三平方の定理と相似を使って行きます。
詳しい解説は必要無いと思うので簡単に済ませますね。
条件
長方形\(\,\mathrm{OABC}\,\)がある。
\(\,\mathrm{OA=4\,,\,OC=4\sqrt{2}}\,\)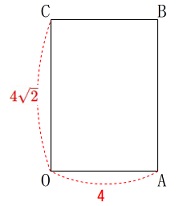
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。
(1)
対角線\(\,\mathrm{AC}\,\)の長さを求めます。
三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{AC^2}&=&\mathrm{OA^2+OC^2}\\
&=&(\,\color{red}{4}\,)^2+(\,\color{red}{4\sqrt{2}}\,)^2\\
&=&48\\
\mathrm{AC}&=&\pm 4\sqrt{3}
\end{eqnarray}\)
長さだから\(\,\mathrm{AC\,＞\,0}\,\)なので
\(\hspace{10pt}\mathrm{AC}=\underline{ 4\sqrt{3} (\mathrm{cm}) }\)
対角線\(\,\mathrm{OB}\,\)も同じ長さです。
これは\(\color{black}{\fbox{1}}\)で出されても良いのですが続き問題の入口です。
(2)
長方形が相似拡大された図形の一部の面積を求めます。
条件
長方形\(\,\mathrm{OABC}\,\)の対角線を長辺とする相似な長方形を\(\,\mathrm{ODEB}\,\)、
長方形\(\,\mathrm{ODEB}\,\)の対角線を長辺とする相似な長方形を\(\,\mathrm{OFGE}\,\)、
対角線\(\,\mathrm{BD}\,\)、\(\,\mathrm{OE}\,\)の交点を\(\,\mathrm{H}\,\)とする。
※
長方形の長辺とは長い方の辺の事です。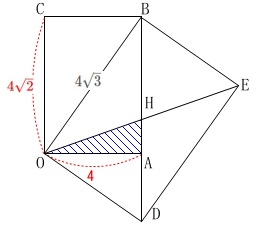
図２を与えてくれているので直感的にも分かりやすいですね。
ただ、順に分かる長さを出していくうちに\(\,\mathrm{OFGE}\,\)の使い道は？
と終わったので深くは考えないことにしました。笑
長さを求めて面積の公式を使う方法
相似比から長さを出していきますが、
簡単に済ませますので計算は自分でもやってみてください。
相似から
\(\begin{eqnarray}\displaystyle
\mathrm{OA:OC}&=&\mathrm{OD:OB}\\
4:4\sqrt{2}&=&\mathrm{OD}:4\sqrt{3}\\
\mathrm{OD}&=&\frac{4\times 4\sqrt{3}}{4\sqrt{2}}\\
&=&\color{magenta}{2\sqrt{6}}
\end{eqnarray}\)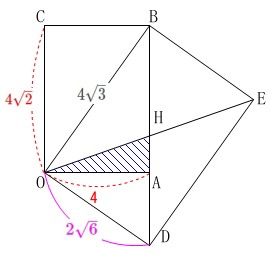
さらに
\(\begin{eqnarray}\displaystyle
\mathrm{OA:OB}&=&\mathrm{OD:OE}\\
4:4\sqrt{3}&=&2\sqrt{6}:\mathrm{OE}\\
\mathrm{OE}&=&\frac{4\sqrt{3}\times 2\sqrt{6}}{4}\\
&=&\color{blue}{6\sqrt{2}}
\end{eqnarray}\)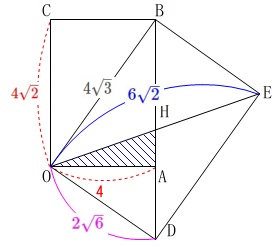
ここで長方形の対角線は等しいので\(\,\mathrm{BD=OE}\,\)で、
対角線の半分だから\(\,\mathrm{OH=HD}=3\sqrt{2}\,\)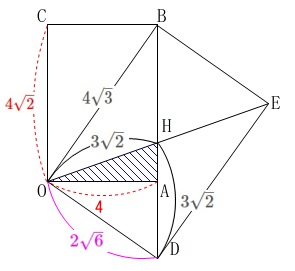
さらに、三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{OH^2}&=&\mathrm{OA^2+AH^2}\\
(3\sqrt{2})^2&=&(4)^2+\mathrm{AH^2}\\
\mathrm{AH^2}&=&18-16\\
&=&2\\
\mathrm{AH}&=&\color{red}{\sqrt{2}} (\,\mathrm{AH}\,＞\,0\,）
\end{eqnarray}\)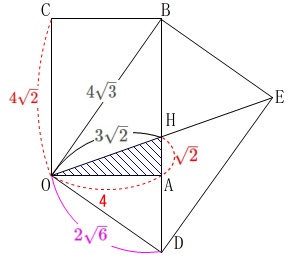
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{△OAH}&=&\frac{1}{2}\times \mathrm{OA}\times \mathrm{AH}\\
&=&\frac{1}{2}\times \color{red}{4}\times \color{red}{\sqrt{2}}\\
&=&\underline{ 2\sqrt{2} (\,\mathrm{cm^2}\,) }
\end{eqnarray}\)
\(\,\mathrm{OD=2\sqrt{6}}\,\)が先に目に入って、
\(\,\mathrm{AD}\,\)を求めにいった人もいると思いますが構いません。
方針が立ったなら突っ走った方が早いです。
(2)（別解）相似比から面積を求める方法
相似な三角形に気がつけば、
面積比と引き算で答えは出ます。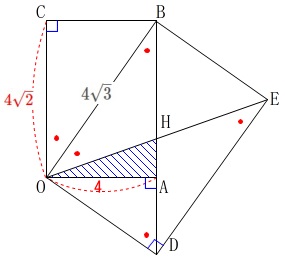
こちらは考えすぎとも言えるので簡単に済ませます。
長方形\(\,\mathrm{OABC}\,\)と\(\,\mathrm{ODEB}\,\)は相似で、
相似比：\(\,4\sqrt{2}:4\sqrt{3}=\sqrt{2}:\sqrt{3}\,\)
なので
面積比：\(\,(\sqrt{2})^2:(\sqrt{3})^2\,=\,2:3\)
このことから長方形\(\,\mathrm{ODEB}\,\)の面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\frac{3}{2}\times 4\times 4\sqrt{2}\\
&=&\color{blue}{24\sqrt{2}}
\end{eqnarray}\)
\(\,\mathrm{△ODH}\,\)の面積は長方形の面積を４等分されるので
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△ODH}}&=&\frac{1}{4}\times \color{blue}{24\sqrt{2}}\\
&=&\color{red}{6\sqrt{2}}
\end{eqnarray}\)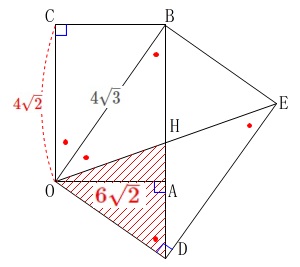
また
\(\,\mathrm{△OAB}\,\)∽\(\,\mathrm{△DAO}\,\)
相似比は
\(\,\mathrm{AB:AO}=4\sqrt{2}:4=\sqrt{2}:1\)
面積比は
\(\hspace{10pt}(\sqrt{2})^2:1^2\,=\,2：1\)
なので
\(\begin{eqnarray}\displaystyle
\mathrm{△DAO}&=&\frac{1}{2}\times \mathrm{△OAB}\\
&=&\frac{1}{2}\times \frac{1}{2}\times 4\times 4\sqrt{2}\\
&=&\color{magenta}{4\sqrt{2}}
\end{eqnarray}\)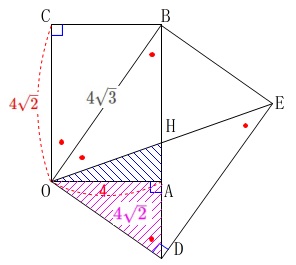
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{△OAH}&=&\mathrm{\color{red}{△ODH}}-\mathrm{\color{magenta}{△DAO}}\\
&=&\color{red}{6\sqrt{2}}-\color{magenta}{4\sqrt{2}}\\
&=&\underline{ 2\sqrt{2} (\mathrm{cm^2} })
\end{eqnarray}\)
ね、考えすぎでしょう？
長方形\(\,\mathrm{OFGE}\,\)があるので本当なら続きがあったのかもしれませんね。
問２場合の数と確率
問２
さいころ２つの問題です。
樹形図で終わりますが、いくつか注意点があります。
大小２つのさいころを投げ、
出た目の和が\(\,n\,\)です。
(1)
条件を満たす\(\,n\,\)をすべて求めます。
条件
\(\,\sqrt{102\,n}\,\)が\(\,a\sqrt{b}\,\)の形で表せる。
\(\,a\,,\,b\,\)は\(\,a＞1\,\)を満たす自然数。
一つ目の注意点ですが\(\,a\,,\,b\,\)は出た目ではありませんよ。
問題によっては「2つのサイコロので目を\(\,a\,,\,b\,\)とする」ことが多いので注意しましょう。
\(\hspace{10pt}\sqrt{102\,n}=\sqrt{2\times 3\times 17\times n}\)
これが\(\,a\sqrt{b}\,\)の形になるということは、
出た目の和\(\,n\,\)は\(\,2\,,\,3\,,\,17\,\)の倍数です。
例えば、
\(\,n=2\,\)のとき\(\,\sqrt{2^2\times 3\times 17}=2\sqrt{3\times 17}\)
となります。
ルートの中に平方となる部分が1つでもできれば
条件を満たすということです。
ただし、\(\,n\,\)が\(\,17\,\)の倍数にはなりません。
さいころの目は最小が\(\,1\,\)で最大が\(\,6\,\)なので
２つのさいころの出た目の和\(\,n\,\)は
\(\hspace{10pt}2\,≦\,n\,≦\,12\)
となるので答えはこの中にあります。
調べても大した数ではありませんよ。
\(\hspace{10pt}n\,=\underline{ \,2\,,\,3\,,\,4\,,\,6\,,\,8\,,\,9\,,\,10\,,\,12 }\)
(2)
「\(\,\sqrt{102\,n}\,\)が\(\,a\sqrt{b}\,\)の形で表せる。」
確率を求めます。
(1)で\(\,n\,\)の場合は出ていますので調べるだけです。
注意点その２です。
「\(\,8\,\)通りの場合を調べる。」
というのが大変だと思う人は、
これからは「たった\(\,8\,\)通り」と考えるようにしましょう。
数年前の北海道大学の入試で鬼のような場合分けがあったのを思い出しました。笑
そもそもさいころ２つでは
３６通りしか考えなくて良いので限定されていますよね。
樹形図で良いですけど出目の和を表で見ます。
縦横のさいころの大小はどちらでも構いません。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& ① & ② & ③ & ④ & ⑤ & ⑥\\ \hline
① & \color{red}{2} & \color{red}{3} & \color{red}{4} & 5 & \color{red}{6} & 7\\ \hline
② & \color{red}{3} & \color{red}{4} & 5 & \color{red}{6} & 7 & \color{red}{8}\\ \hline
③ & \color{red}{4} & 5 & \color{red}{6} & 7 & \color{red}{8} & \color{red}{9}\\ \hline
④ & 5 & \color{red}{6} & 7 & \color{red}{8} & \color{red}{9} & \color{red}{10}\\ \hline
⑤ & \color{red}{6} & 7 & \color{red}{8} & \color{red}{9} & \color{red}{10} & 11\\ \hline
⑥ & 7 & \color{red}{8} & \color{red}{9} & \color{red}{10} & 11 & \color{red}{12} \\ \hline
\end{array}\)
和の赤い数字の組が条件を満たします。
（\(\,2\,\)か\(\,3\,\)で割れる数）
答え \(\hspace{10pt}\displaystyle \frac{24}{36}=\underline{\underline{ \frac{2}{3} }}\)
黒字を数えた方が早いですね。笑
\(\hspace{4pt}\displaystyle 1-\frac{12}{36}=1-\frac{1}{3}=\underline{\underline{ \frac{2}{3} }}\)
（余事象の確率を利用しています。）
以上です。
比較的にとりやすい問題になっている？と思えますが、
問題への取り組み方で差がついたでしょう。
前半から見直してみて下さい。
共通問題の特徴と試験時間の延長は何のためか少しは見えてくるでしょう。
前半 ⇒ 2022年(令和4年)度北海道公立高校入試問題の数学の問題と解説
目標点数によりますが、
過去問から傾向を探るなら裁量問題にも目は通しておくことをおすすめします。
年度によって多少の違いは出てきますが、
問題の量や質は全体ではそれほど変わりはしないと思います。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
