2018年東京都公立高校入試前期試験の大問3関数の解説

2018年に東京都で行われた公立高校入試前期試験の大問3の解説です。
大問3は関数総合問題で変域、直線の方程式、文字を使った座標の利用方法です。
関数問題のポイントになるのは点です。

⇒　東京都2018前期数学問題　

変域を求める問題

　\(\color{black}{\fbox{ 3 }}\)

\(\,問1\,\)は変域を求める問題です。

高校入試の関数問題にはグラフが書いてあります。
ただし、座標が書かれていません。

図形問題でもそうですが情報は書き込む、
それが答えを導くためのポイントになります。

　座標を書き込む

関数問題のはじめはここからです。
\(\,問1\,\)の前に条件があります。

　曲線\(\,\ell\,\)は\(\,\displaystyle y=\frac{1}{2}x^2\,\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-4\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,6\,\)
　点\(\,\mathrm{P}\,\)は曲線\(\,\ell\,\)上の点

このように\(\,\color{red}{x}\,\)座標だけが与えられることが多いですが、
曲線上の点なので\(\,\color{blue}{y}\,\)座標もわかります。

　\(\,x=-4\,\)のとき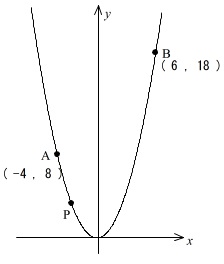
　\(\begin{eqnarray}
\displaystyle y&=&\frac{1}{2}\times (-4)^2\\
&=&\frac{1}{2}\times 16\\
&=&8
\end{eqnarray}\)

なので　\(\,\mathrm{\color{red}{A}}\,\color{red}{(\,-4\,,\,8\,)}\,\)

　\(\,x=6\,\)のとき
　\(\begin{eqnarray}
\displaystyle y&=&\frac{1}{2}\times (6)^2\\
&=&\frac{1}{2}\times 36\\
&=&18
\end{eqnarray}\)

なので　\(\,\mathrm{\color{red}{B}}\,\color{red}{(\,6\,,\,18\,)}\,\)

この座標を書いておくことでずいぶん変わりますよ。

\(\,問1\,\)は、\(\,x\,\)座標\(\,y\,\)座標が\(\,a,b\,\)に置き換わっているので見にくいですが、
　\(\,\mathrm{P}\,(\,a\,,\,b\,)\,\)
としたときのPの動ける範囲を聞いているだけで、
単に\(\,y\,\)の変域を聞いているだけです。

　\(\,-4≦a≦6\,\)　のとき
つまり
　\(\,-4≦x≦6\,\)　のときの
　\(\displaystyle y=\frac{1}{2}x^2\)
の\(\,y\,\)の変域（\(\,b\,\)の変域）を答えれば良いのです。

注意するのは、\(\,\color{red}{最小値は8ではない}\,\)ことです。
\(\,y\,\)の変域は一度減少して、増加しているので、一番小さいのは\(\,x=-4\,\)のときではありません。

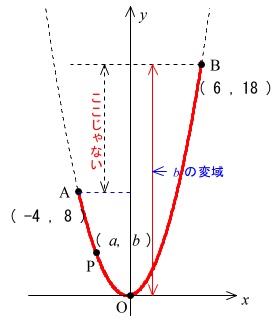
　\(\,\underline{0≦b≦18}\,\)

このちょっとした勘違いをするのはグラフを書かないからです。
それか、\(\,y\,\)の変域の意味を勘違いしているかですね。

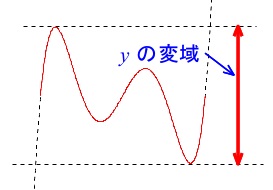
\(\,y\,\)の変域は途中も含めて上下に動ける範囲のことです。
両端が最小、最大になるとは限りません。
　

直線の方程式の求め方

\(\,問2\,\)では条件が増えます。

　\(\,\mathrm{P}\,\)の動く範囲\(\,-4＜x＜6\,\)
　直線\(\,\mathrm{AB}\,\)上で\(\,\mathrm{P}\,\)と同じ\(\,x\,\)座標の点を\(\,\mathrm{Q}\,\)
　\(\,\mathrm{PQ}\,\)の中点を\(\,\mathrm{M}\,\)

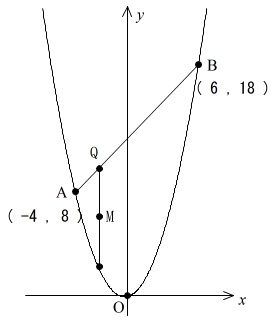
①「\(\,\mathrm{P}\,\)が\(\,y\,\)軸上にあるとき」
つまり
　\(\,x=0\,\)のとき
ということです。
　
　\(\,x=0\,\)のとき\(\,\mathrm{Q}\,\)は直線\(\,\mathrm{AB}\,\)の\(\,y\,\)切片となります。

直線\(\,\mathrm{AB}\,\)は\(\,2\,\)点
　\(\,(\,-4\,,\,8\,)\,\) , \(\,(\,6\,,\,18\,)\,\)
を通ります。
直線\(\,\mathrm{AB}\,\)を\(\,y=ax+b\,\)とおいて
連立方程式を解いても良いですが、傾きから求めましょう。
※
この直線を求める部分は当会では非常に重要視しています。
基礎レポート『1次関数』は必ず見直しておいてください。

1次関数では傾きと変化の割合は同じ値です。

　\(\,\displaystyle \color{red}{傾き=変化の割合=\frac{　y\,の増加量　}{　x\,の増加量　}}\,\)

　\(\,(\,-4\,,\,8\,)\,\)
　\(\,(\hspace{8pt}6\,,\,18\,)\,\)

と縦に並べて\(\,x,y\,\)座標とも下から上を引きます。
上から下からも良いですが、\(\,x\,\)と\(\,y\,\)で方向を変えると変化の割合の符号が逆になります。

　\(\,x\,の増加量=6-(-4)=10\)
　\(\,y\,の増加量=18-(8)=10\)

よって傾きは　\(\,\displaystyle \frac{10}{10}=1\,\)

　\(\,y=x+b\,\)

となりますが、これに2点\(\,\mathrm{A,B}\,\)のどちらかを代入して\(\,b\,\)を決めます。
\(\,\mathrm{A,B}\,\)どちらを入れても同じ値が出ないとおかしいです。

　\(\,\mathrm{\color{red}{B}}\,\color{red}{(\,6\,,\,18\,)}\,\)

を代入すると

　\(\begin{eqnarray}
y&=&x+b\\
18&=&6+b\\
b&=&12
\end{eqnarray}\)

直線\(\,\mathrm{AB}\,\)は
　\(\,y=x+12\,\)
となるので点\(\,\mathrm{Q}\,\)は
　\(\mathrm{Q}\,(\,0\,,\,12\,)\,\)

この2点を通る直線を求めることはほとんどの関数問題では必要になると考えて良いです。
1次関数の確認もできるので総合問題となる入試では2次関数に混じって出ます。
問題によっては何本も直線の方程式を求めることになります。
問題に書いていなくても求めないと答えが出ないので自分で判断して求めることになりますよ。

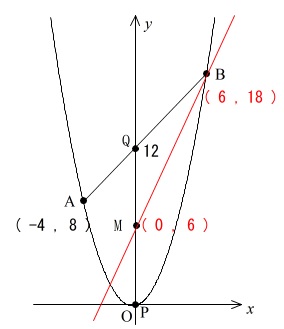
この直線\(\,\mathrm{BM}\,\)が①の答えです。
2点
　\(\,(\,0\,,\,6\,)\,\)
　\(\,(\,6\,,\,18\,)\,\)
を通るので
　\(\displaystyle \,傾き=\frac{18-6}{6-0}=2\,\)

　\(\,y=2x+b\,\)　となりますが切片は\(\,\mathrm{M}\,\)とわかっているので

　\(\,\underline{y=2x+6}\,\)

文字で表した座標の求め方

②直線\(\,\mathrm{BM}\,\)が原点を通るときの点\(\,\mathrm{P}\,\)の座標です。

こういう問題は文字だけ見てても見えてきません。
グラフに書きこんでおおよその位置を確認すると良いです。
頭の中で確認できるようになっても書いた方がはやいし確実です。

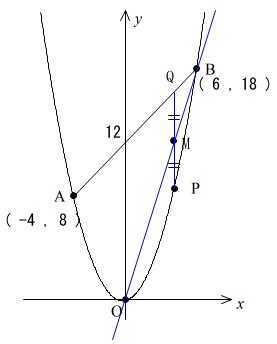
直線\(\,\mathrm{BM}\,\)が原点を通るということで、\(\,\mathrm{M}\,\)が原点にあるわけではありません。
位置関係をしっかり見ておきましょう。

直線\(\,\mathrm{BM}\,\)は原点と\(\,\mathrm{B}\,\)を通る直線なので比例です。

　\(\,\mathrm{O}(\,0\,,\,0\,)\,\)
　\(\,\mathrm{B}(\,6\,,\,18\,)\,\)
より
　
　直線\(\mathrm{BM}：\,y=3x\,\)

ここで\(\,\mathrm{P}\,\)と\(\,\mathrm{M}\,\)と\(\,\mathrm{Q}\,\)は\(\,x\,\)座標が同じなので、
\(\,\mathrm{P}\)の\(\,x\,\)座標を\(\,a\,\)とすると（問1でも同じ設定）

\(\,\mathrm{P}\,\)は曲線\(\,\ell\,\)上の点なので
　\(\,\color{red}{\mathrm{P}\,(\,a\,,\,\frac{1}{2}a^2\,)}\,\)

\(\,\mathrm{Q}\,\)は直線\(\,\mathrm{AB}\,\)上の点なので
　\(\,\color{red}{\mathrm{Q}\,(\,a\,,\,a+12\,)}\,\)

\(\,\mathrm{M}\,\)は直線\(\,\mathrm{OB}\,\)上の点なので
　\(\,\color{red}{\mathrm{M}\,(\,a\,,\,3a\,)}\,\)

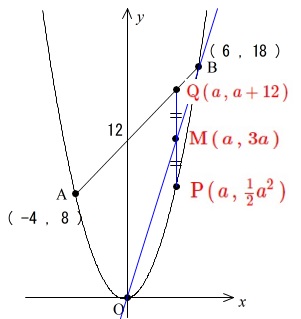
ここからは分かれます。
\(\,\mathrm{M}\,\)が\(\,\mathrm{P,Q}\,\)の中点だということを利用するのは同じですが、

　\(\,\displaystyle \mathrm{\frac{P+Q}{2}=M}\,　･･･①\)
とするか
　\(\,\mathrm{QM=MP}\,　･･･②\)
です。

結果は同じことなのですが計算過程が変わるのと、
①は中点や等分される場合しか使えないのに対し、
②は具体的な長さで与えられた場合など、中点でない場合も使えるという違いがあります。

ここでは②の方法を使います。

線分の長さは\(\,y\,\)座標の差になるので
　\(\,\mathrm{QM}=(a+12)-(3a)\,\)
　\(\,\displaystyle \mathrm{MP}=(3a)-\left(\,\frac{1}{2}a^2\,\right)\,\)

これらが等しい場合なので
　\(\begin{eqnarray}
\displaystyle (a+12)-(3a)&=&(3a)-\left(\,\frac{1}{2}a^2\,\right)\\
a+12-3a&=&3a-\frac{1}{2}a^2\\
-2a+12&=&3a-\frac{1}{2}a^2\\
-4a+24&=&6a-a^2\\
a^2-6a-4a+24&=&0\\
a^2-10a+24&=&0\\
(a-4)(a-6)&=&0\\
a&=&4\,,\,6
\end{eqnarray}\)

あれ？2つ？
と思った人は良い感じですが条件を見落としています。

　「\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,-4\,\)より大きく\(\,6\,\)より小さい」
　　\(-4＜x＜6\)

「より小さい」は\(\,6\,\)を含みません。

よって　\(\,a=4\,\)

このとき\(\,\displaystyle \mathrm{P}\,\left(\,a\,,\,\frac{1}{2}a^2\,\right)\,\)は

　\(\,\mathrm{P}\,\underline{(\,4\,,\,8\,)}\,\)　

関数で文字の設定になれたら公立入試で捨てる問題が減るだけじゃなく、
高校の数学で活躍します。

『超え太郎』－「座標と図形」シリーズは見ておくことをおすすめします。

⇒　数学短期攻略教材『覚え太郎』

できれば高校入試を楽にしておきたいですが、高校数学で活用するために高校に入学してからでも良いです。

⇒　2018年東京都公立高校入試前期問題の大問４平面図形の解説

問4は平面図形の問題です。