2018年東京都公立高校入試前期問題の大問４平面図形の解説

２０１８年東京都で行われた公立入試前期問題の大問４の解説です、
大問４は平面図形の総合問題です。
角度、合同、面積比とありますが、図形問題ですることは１つです。

⇒　2018東京都立高校入試前期の数学問題

　\(\large{\color{black}{\fbox{　4　}}}\)

角度を文字で表す問題

角度が具体的な数値ではなく文字を使って表される問題です。

図を与えてくれていますが条件すべては書き込んでありませんので、
条件を書き込むことから始めます。
条件は
　
　\(\,\mathrm{AB}\,\)は直径
　\(\,\stackrel{ \Large \frown }{ \mathrm{AC} }\,=\,\stackrel{ \Large \frown }{ \mathrm{BC} }\,\)
　
だけですね。
これだけでもいろいろなことが分かります。
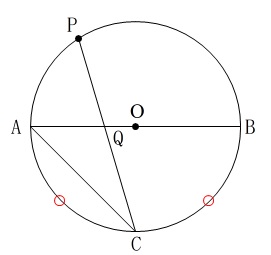書き込むことが多いので問題に合わせて書き込むことにします。

〔\(\,問1\,\)〕
\(\,\mathrm{∠ACP}=a^{\circ}\,\)とするときに、\(\,\mathrm{∠AQP}\,\)の大きさを\(\,a\,\)で表す問題です。

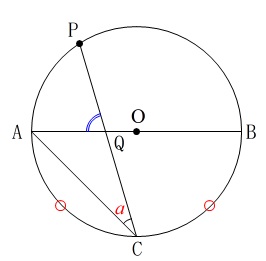　条件　\(\,\stackrel{ \Large \frown }{ \mathrm{AC} }\,=\,\stackrel{ \Large \frown }{ \mathrm{BC} }\,\)を使っていません。

　「2つの弧が等しい」
ということから言えるのは
　「2つの弧に対する円周角と中心角は等しい」
ということです。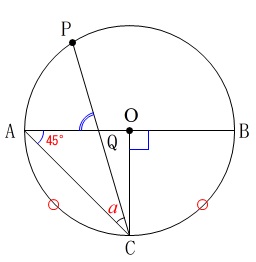
半径は常に等しいから\(\,\mathrm{△ACO}\,\)は直角に等辺三角形になるので

　\(\,\mathrm{∠ACQ}=45^{\circ}\,\)

よって　\(\,\mathrm{∠AQP}=\underline{(45+a)度}\,\)

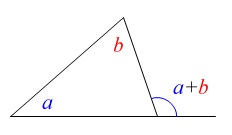
　\(\,\mathrm{∠OCA}=45^{\circ}\,\)
なので
　\(\,\mathrm{∠OCQ}=45^{\circ}-a^{\circ}\,\)
と表せるから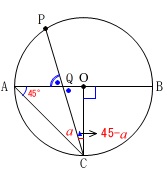
　\(\begin{eqnarray}
\mathrm{∠OCQ+∠OQC}&=&90^{\circ}\\
(45^{\circ}-a^{\circ})+\mathrm{∠OQC}&=&90^{\circ}\\
\mathrm{∠OQC}&=&90^{\circ}-(45^{\circ}-a^{\circ})\\
&=&(\underline{45+a})(度）\\
&=&\mathrm{∠AQP}（対頂角）
\end{eqnarray}\)

でも良いですけど、ここまできたら三角形の外角の性質を利用できるようになっておきましょう。

合同の証明ポイント

〔\(\,問2\,\)〕①
図形の証明は図の中で証明すべきことを完成させておくことがポイントです。
後はその図の中に書き込んだことを日本語を足して説明していけば良いだけです。

問題にある条件を図示していきましょう。
条件は\(\,問1\,\)の前にあるものも全体通じていえる条件ですよ。
\(\,問2\,\)では追加して

　\(\,\mathrm{BP=RP}\,\)
分かることを書き足して行きましょう。

　\(\,\color{red}{直径に対する円周角は90°}\,\)

これで合同の証明は終わりです。

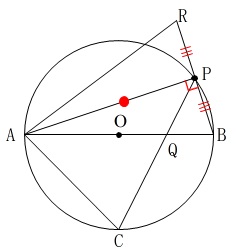
\(\,\mathrm{AP}\,\)は共通なので\(\,2\,\)辺とその間の角がそれぞれ等しくなっています。

合同の証明や相似の証明では記号の順番もそろえなければなりませんので注意してください。
（証明）
　\(\,\mathrm{△\color{red}{A}\color{blue}{B}\color{magenta}{P}}\,\)と\(\,\mathrm{△\color{red}{A}\color{blue}{R}\color{magenta}{P}}\,\)において
　\(\,\mathrm{\color{blue}{B}\color{magenta}{P}=\color{blue}{R}\color{magenta}{P}}　（仮定）　　　･･･①\,\)
　\(\,\mathrm{\color{red}{A}\color{magenta}{P}=\color{red}{A}\color{magenta}{P}}　（共通な辺）　･･･②\,\)
また直径に対する円周角は\(\,90°\,\)なので
　\(\,\mathrm{∠\color{red}{A}\color{magenta}{P}\color{blue}{B}=∠\color{red}{A}\color{magenta}{P}\color{blue}{R}}=90°　･･･③\,\)
①②③より
　二組の辺とその間の角がそれぞれ等しい。
よって
　\(\,\mathrm{△\color{red}{A}\color{blue}{B}\color{magenta}{P}}\equiv\mathrm{△\color{red}{A}\color{blue}{R}\color{magenta}{P}}　（終わり）\,\)

順番の確認のために色分けしましたが実際には必要ありません。
ただ、証明のときは順番をそろえなければならない、
ということは示そうとしている等しい辺や角では、
　左辺と右辺の順番は一致している
ということです。

証明すべき合同な三角形があれば、どことどこが等しいはずなのか図の中でみておくと、示せば良いことが見つかりやすくなります。

　\(\,\mathrm{△\color{red}{A}B\color{blue}{C}}\,\equiv\,\mathrm{△\color{red}{D}E\color{blue}{F}}\,\)

を示すのであれば

　\(\begin{eqnarray}
\mathrm{\color{red}{A}B}&=&\mathrm{\color{red}{D}E}\\
\mathrm{B\color{blue}{C}}&=&\mathrm{E\color{blue}{F}}\\
\mathrm{\color{blue}{C}\color{red}{A}}&=&\mathrm{\color{blue}{F}\color{red}{D}}\\
\mathrm{∠B\color{red}{A}\color{blue}{C}}&=&\mathrm{∠E\color{red}{D}\color{blue}{F}}\\
\mathrm{∠\color{red}{A}B\color{blue}{C}}&=&\mathrm{∠\color{red}{D}E\color{blue}{F}}\\
\mathrm{∠\color{red}{A}\color{blue}{C}B}&=&\mathrm{∠\color{red}{D}\color{blue}{F}E}
\end{eqnarray}\)

となっているはずなので、等しいことを示せる辺や角を見つけていくというのも方法の1つです。

三角形と四角形の面積比

〔\(\,問2\,\)〕②
三角形と四角形の面積比です。
\(\,問2①\,\)に条件が加わります。

　　\(\,\stackrel{ \Large \frown }{ \mathrm{BC} }\,=\,2\stackrel{ \Large \frown }{ \mathrm{BP} }\,\)

弧の長さの比を与えてくれているということは
　円周角か中心角の比
に着目するように教えてくれているのと同じです。
ここまでくれば作業するかどうかなので簡単に説明していいでしょう。
\(\,問1\,\)からの条件を図に書き込んでみてください。
　　\(\,\stackrel{ \Large \frown }{ \mathrm{BC} }\,=\,2\stackrel{ \Large \frown }{ \mathrm{BP} }\,\)
なので弧\(\,\mathrm{PB}\,\)の中心角と弧\(\,\mathrm{BC}\,\)の円周角が等しくなります。
　\(\,\mathrm{∠POB=∠BAC}\,\)

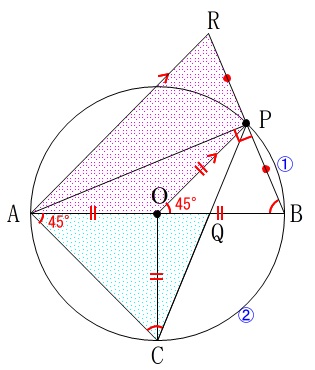
直接は面積比較できないのでどこかに基準を作るか、具体的な数値で求めるかです。
方法はいろいろと考えられます。

この問題は長さの数値が1つもありませんので、自分で簡単な数値を当てはめても面積比は変わりませんよ。

ここでは文字を使って一般的に面積比を出しておきます。
図の中に相似な三角形があるので抜き出して面積比につなげるのがはやいでしょう。

　中点連結定理から
　　\(\,\mathrm{PO}\,/\!/\,\mathrm{RA}\,\)
　　\(\,\mathrm{△BPO}\,\)　∽　\(\,\mathrm{△BRA}\,\)

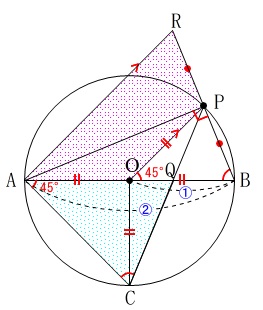
面積比は相似比が\(\,\color{blue}{①：②}\,\)であることから
　　\(\mathrm{△BPO}:\mathrm{△BRA}=\color{blue}{①:④}\)
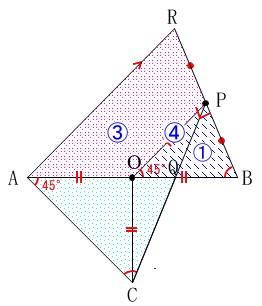このことから
　\(\,四角形\,\mathrm{AOPR}\,=\mathrm{△BRA-△BPO}\,\)
なので
　\(\,\mathrm{△POB}:四角形\,\mathrm{AOPR}\,=\color{blue}{①:③}\,\)

ここまでくれば基準を\(\,\mathrm{△POB}\,\)にしようという気になるでしょう。

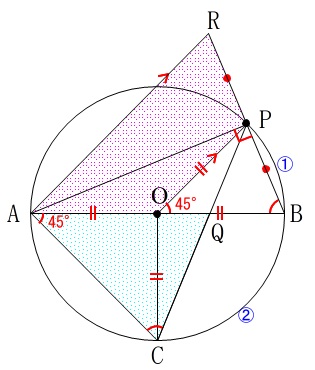
　弧\(\,\mathrm{PA}\,\)の円周角から
　　\(\,\mathrm{∠OBP=∠ACQ}\,\)
　　\(\,\mathrm{△OBP}\,\)　∽　\(\,\mathrm{△ACQ}\,\)

問題になるのはこの2つの三角形の相似比が出ていないことです。
そこでこの円の半径を\(\,r\,\)とおきます。

直角二等辺三角形\(\,\mathrm{OAC}\,\)から
　\(\,\mathrm{AC}=\sqrt{2}r\,\)
対応する辺\(\,\mathrm{OB}\,\)は半径\(\,r\,\)に等しいので
　\(\,\mathrm{\color{blue}{△OBP}}\,\)　と　\(\,\mathrm{\color{green}{△ACQ}}\,\)
の相似比は
　\(r:\sqrt{2}r=\color{blue}{1}:\color{green}{\sqrt{2}}\)

相似比が\(\,\color{blue}{1}:\color{green}{\sqrt{2}}\,\)なので
　\(\,\mathrm{△OBP}\,\)と\(\,\mathrm{△ACQ}\,\)の面積比は
　　\(\,\color{blue}{1}^2:(\color{green}{\sqrt{2}})^2=\color{blue}{①}:\color{green}{②}\,\)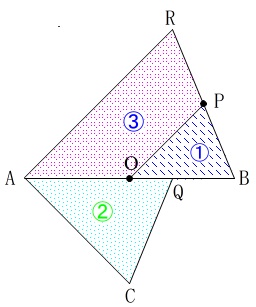
\(\,\mathrm{△ACQ}\,\)の面積\(\,\color{blue}{②}\,\)は四角形\(\,\mathrm{AOPR}\,\)の面積\(\,\color{green}{③}\,\)の
　\(\displaystyle \underline{\frac{2}{3}\,倍}\)　

他にもいろいろな方法が考えられます。
　補助線を引くなら平行線か垂線
とお伝えしているので半径を\(\,r\,\)とした後、垂線を引いてみると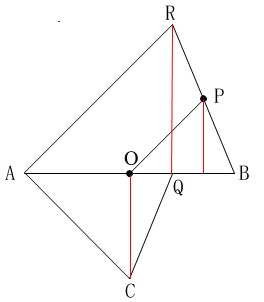
3つの三角形の面積が\(\,r\,\)を使って求まります。
（\(\,r\,\)とおかなくても面積比は出ます。）

　\(\begin{eqnarray}
\displaystyle \mathrm{△OBP}&=&\frac{1}{2}\times r\times \frac{1}{\sqrt{2}}r\\
&=&\frac{\sqrt{2}}{4}r^2
\end{eqnarray}\)

　\(\begin{eqnarray}
\displaystyle \mathrm{△BRA}&=&\frac{1}{2}\times 2r\times \sqrt{2}r\\
&=&\sqrt{2}r^2
\end{eqnarray}\)

　\(\begin{eqnarray}
\displaystyle \mathrm{△ACQ}&=&\frac{1}{2}\times \sqrt{2}\times r\\
&=&\frac{\sqrt{2}}{2}r^2
\end{eqnarray}\)

となるので三角形から三角形を引いて、面積比を出せば答えは同じものが出てきますのでやってみてください。
3つの三角形はすべて相似になるので、他にも簡単に比が出せる方法はあります。
自分にできそうな方法をいろいろ試してみると良いです。

試験会場ではあれこれやる余裕がないでしょうから、
「これで行こう」
と決めたら突っ走った方がはやいかもしれません。

問題はいろいろな解法で答えが出るように設定してくれていますが、
基本的な定理は使いますので覚えて、使えるようになっておくことです。

試験の結果は受験までにどれだけ準備したかで決まっているのです。

⇒　2018年東京都公立高校入試の前期問題問5空間図形の解説

\(\color{black}{\fbox{　5　}}\)は空間図形ですが数字がきれいなので取り組みやすいです。

⇒　東京都公立高校入試数学の過去問と解答解説

内容、計算量ともに都立入試では同じレベルの問題が多いです。