令和４年度埼玉県公立高校入試数学【学校選択問題】の解説【前半】

令和４年（２０２２年）度埼玉県公立高校入試数学【学校選択問題】前半の解説です。
学校選択問題を選択する時点である程度の基礎はできいるとして要点だけをおさえた解説とします。
【前半】は配点の半分以上となる第１問第２問とします。
例年通り一般入試問題との重複がありますので省略する部分があります。
一般入試と重なる問題は別解を示すところもありますので参考にしてください。

２０２２（令和４年）度埼玉県公立高校入試の数学【学校選択】の問題

試験での注意点は例年通りです。

⇒　２０２２（令和４年）度埼玉県公立高校入試の数学【学校選択】の問題

問題は\(\,\large{1}\,\)から\(\,\large{5}\,\)まであります。

２０２２年度埼玉県公立高校入試の数学【学校選択問題】の解説

一般入試と重なる部分は略解とします。

学校選択問題で高得点とるためには基礎に加えある程度の作業が必要です。
一般入試と同じですが逆に試験時間は\(\,50\,\)分しかないと考え、
試験の受け方に注意した方が良いですね。
会員は『最大得点法』で確認しておいてください。

問題構成や配点については詳しく書きませんので、
対策としての確認はご自身でお願い致します。

第１問

\(\,\large{1}\,\)

(1)
　\(\hspace{10pt}\displaystyle 6xy^2\div \left(\,-\frac{3}{5}xy\,\right)\div (\,-2x\,)^3\\
\displaystyle =6xy^2\times \frac{5}{3xy}\times \frac{1}{8x^3}\\
\displaystyle =\underline{\underline{　\frac{5\,y}{4\,x^3}　}}\)

全体の符号が\(\,+\,\)であることを最初に確認すると良いです。

(2)
ある程度の推測からで良いです。

おおよそですが\(\,\sqrt{11}=3.\cdots \,\)です。
　\(\hspace{4pt}\sqrt{9}\,＜\,\sqrt{11}\,＜\,\sqrt{16}\)

\(\,整数部分\,+\,小数部分\,\)が全体なので
整数部分\(\,a\,\)と小数部分\(\,b\,\)は
　\(\hspace{10pt}a=\color{blue}{3}\)
　\(\hspace{10pt}b=\sqrt{11}-3\)

与式（求値式）に直接代入してもしれていますが、
\(\,b\,\)の変形が先なのは会員にはおなじみでしょう。
　\(\begin{eqnarray}\displaystyle
b&=&\sqrt{11}-3\\
b+3&=&\sqrt{11}\end{eqnarray}\)
両辺平方して
　\(\begin{eqnarray}\displaystyle (b+3)^2&=&11\\
b^2+6b+9&=&11\\
b^2+6b&=&\color{red}{2}
\end{eqnarray}\)

これから
　\(\hspace{10pt}a^2-b^2-6b\\
=a^2-(b^2+6b)\\
=(\color{blue}{3})^2-(\,\color{red}{2}\,)=\underline{　7　}\)

代入して算数でも良いですが、数学しましょう。

(3)
２つやっておきます。

展開して整理すると
　\(\begin{eqnarray}\displaystyle
2(x+3)^2-3(x+3)-3&=&0\\
2x^2+12x+18-3x-9-3&=&0\\
2x^2+9x+6&=&0\end{eqnarray}\)
解の公式から
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-9\pm \sqrt{81-4\cdot 2\cdot 6}}{2\times 2}\\
&=&\underline{\underline{　\frac{-9\pm \sqrt{33}}{4}　}}
\end{eqnarray}\)

まとまりに注目すると\(\,x+3=a\,\)として
　\(\hspace{4pt}2a^2-3a-3=0\)
いったん\(\,a\,\)の方程式として解の公式から
　\(\begin{eqnarray}\displaystyle
a&=&\frac{3\pm \sqrt{3^2-4\cdot 2\cdot (-3)}}{2\times 2}\\
&=&\frac{3\pm \sqrt{33}}{4}\\
\end{eqnarray}\)
元にもどすと
　\(\begin{eqnarray}\displaystyle
x+3&=&\frac{3\pm \sqrt{33}}{4}\\
x&=&\underline{\underline{　\frac{-9\pm \sqrt{33}}{4}　}}
\end{eqnarray}\)

これは計算過程を考えてもどちらでも良いです。
迷うくらいなら突っ走ってしまいましょう。
両方でミスの確認するのが一番良いですが、
目標点数に対する時間の配分によりますね。

(4)
ん？これはどこかで見たことがありますね。
一般入試問題大問\(\,\large{1}\,\)の(12)と同じです。
　\(\hspace{10pt}540=2^2\times 3^3\times 5\)

平方数を残すように\(\,n\,\)で割れば良いので
　\(\hspace{10pt}\underline{　4　}(通り)\)

⇒　令和４年（２０２２）度埼玉県公立高校入試数学【一般問題】の解説

わかりにくい場合は一般入試の解説を参考にしてください。

(5)
これも一般入試問題大問\(\,\large{1}\,\)の(13)と同じです。
相似な三角形を書き出しましょう。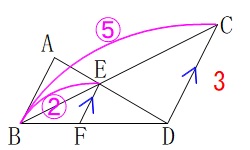一般入試では違う相似を利用したので、
こちらではもう一方を利用しておきます。
　\(\,\mathrm{△BEF}\,\)　∽　\(\,\mathrm{△BCD}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{BE:BC}&=&\mathrm{FE:DC}\\
2:5&=&\mathrm{FE}:3\\
5\times \mathrm{FE}&=&2\times 3\\
\mathrm{FE}&=&\underline{\underline{　\frac{6}{5}　(\mathrm{cm})}}
\end{eqnarray}\)

(6)
一般問題の(14)と同じです。
中央値と平均値は一致するとは限りません。
答え　\(\,\underline{　ウ　}\,\)

(7)
挿絵はありませんが、一般問題の(15)と同じです。
繁殖池にいる魚の総数を\(\,x\,\)とすると
　\(\begin{eqnarray}\displaystyle
x:22&=&23:3\\
x&=&\frac{22\times 23}{3}\\
&=&168.6\cdots
\end{eqnarray}\)

答え　およそ\(\,\underline{　169　}\,\)　（匹）

一般入試の解説では比例関係の便利な計算式を紹介しています。
興味のある方は確認しておくと良いです。
（理科でめちゃくちゃ役に立ちますが他ではめったに見ることは無いでしょう。）

(8)
１次方程式でもいいですが連立方程式で進めます。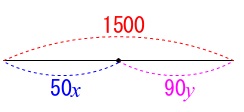歩いた時間を\(\,\color{blue}{x}\,\)分、走った時間を\(\,\color{magenta}{y}\,\)分とします。
移動した時間の和は\(\,24\,\)分なので
　\( \begin{cases}
\hspace{4pt} x+y=24\\
\hspace{4pt} 50\,x+90\,y=1500
\end{cases}\)
解き方は加減法でも代入法でも良いです。
　\(\hspace{10pt}x=16.5\,,\,y=7.5\)

歩き始めてから\(\,16.5\,\)分後に走り始めているので
　\(\hspace{10pt}\underline{　午後\,1\,時\,16\,分\,30\,秒　}\)

(9)
一般入試に似ていますが２次関数が加わります。
考え方は同じで良いです。
　曲線\(\,①\,\)：\(\,y=a\,x^2\,\)
　曲線\(\,②\,\)：\(\displaystyle \,y=\frac{b}{x}\)
　直線\(\,\ell\,\)：\(\,y=c\,x+d\)
　点\(\,\mathrm{P}\,\)で３つの曲線が交わり\(\,x\,\)座標が\(\,-1\,\)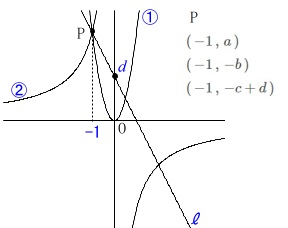点\(\,\mathrm{P}\,\)は\(\,a\,,\,b\,,\,c\,,\,d\,\)を使って表すと
　\((\,-1\,,\,a\,)\)
　\((\,-1\,,\,-b\,)\)
　\((\,-1\,,\,-c+d\,)\)
となりますが全て同じ点です。

つまり\(\,y\,\)座標は全て同じなので、
直線\(\,\ell\,\)の\(\,y\,\)切片\(\,d\,\)が正で\(\,a\,\)より小さいこと、
および\(\,-b=-c+d\,\)から
（\(\,b\,,\,c\,\)は負であることはグラフからも分かる）
　\(\hspace{4pt}\underline{　b\,＜\,c\,＜\,d\,＜\,a　}\)

比例定数などを適当な整数で数字を合わせても大小関係は出せますよ。
一般的に成り立つ関係なので具体的にも成り立ちます。

(10)
アイスクリームの絵はありませんけど一般入試の(16)と同じです。
そもそもアイスクリームでなくても良い。

体積比と価格を比較すれば割安なのはどれかが分かります。
もちろん単位体積に対して価格が安いのが割安です。
逆に見れば価格比に対し体積比が大きいのが割安ということです。
　\(\begin{array}{|c|c|c|c|} \hline
　サイズ　 &　 \mathrm{S}　 &　 \mathrm{M}　 & 　\mathrm{L}　 \\ \hline
価格 & 160 & 320 & 960 \\ \hline
体積比 & 27 & 64 & 200 \\ \hline
\end{array}\)
価格比に対し体積比は\(\,\mathrm{L}\,\)が一番大きいので、
最も割安なサイズは\(\,\mathrm{\underline{　L　}}\,\)です。

『理由を説明しなさい。』となっていますので、
２つずつの比較でも、
体積比で割って数値で示すでも良いですよ。
（小数が出てきて割り算がメンドウだけど。）

買い物するならお得に買いたいですが、
余って捨てるようだと無駄になりますので気をつけましょう。

第２問

\(\,\large{2}\,\)
作図と比例定数を求める関数の問題があります。

(1)
一般問題と考え方は同じで良いですね。
線分\(\,\mathrm{AB}\,\)上に\(\,\mathrm{AC:AB=\color{red}{1}:\color{blue}{\sqrt{2}}}\,\)となる点\(\,\mathrm{C}\,\)の作図です。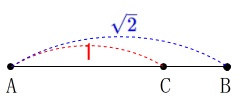ただし、同一直線上に線分比を作るので逆の作業となります。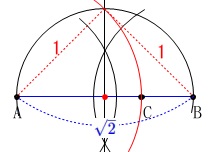線分\(\,\mathrm{AB}\,\)が\(\,\mathrm{\sqrt{2}}\,\)となるので、
線分\(\,\mathrm{AB}\,\)が直角二等辺三角形の斜辺になれば良いわけです。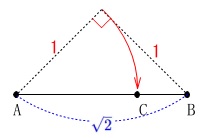
線分\(\,\mathrm{AB}\,\)の垂直二等分線と、
線分\(\,\mathrm{AB}\,\)を直径とする円との交点を見つけ、
点\(\,\mathrm{A}\,\)から交点までを\(\,\mathrm{AC}\,\)の長さにします。

作図には点線で書いた線分は必要ありません。

(2)
関数のグラフ上の問題ですが図形的な性質が出てきます。

問題にある条件をグラフ上に示しておきます。
条件
　曲線の関数：\(\,y=a\,x^2\,(\,a\,＞\,0\,)\)
　２点\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標は\(\,-3\,,\,3\,\)
　\(\,\mathrm{D}\,\)は\(\,\mathrm{C}\,\)と\(\,y\,\)座標が等しい\(\,y\,\)軸上の点
　\(\,\mathrm{AE=EC}\,\)
　\(\,\mathrm{AC}\,\)⊥\(\,\mathrm{BD}\,\)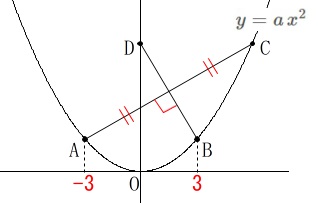図形の性質を見ておくと、
\(\,y\,\)座標が等しく\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)なので
　\(\,\mathrm{△AEB}\,\)　≡　\(\,\mathrm{△CED}\,\)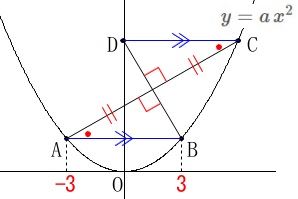つまり四角形\(\,\mathrm{ABCD}\,\)はひし形ですね。

ここからは座標を見ていきましょう。
関数\(\,y=a\,x^2\,\)や\(\,\mathrm{ABCD}\,\)が平行四辺形であることから
　\(\,\mathrm{A}\,(\,-3\,,\,9\,a\,)\,\)
　\(\,\mathrm{B}\,(\,3\,,\,9\,a\,)\,\)
　\(\,\mathrm{C}\,(\,6\,,\,36\,a\,)\,\)
　\(\,\mathrm{D}\,(\,0\,,\,36\,a\,)\,\)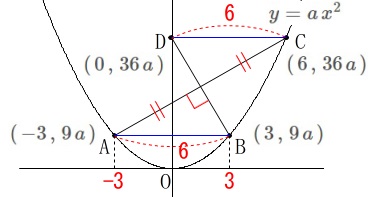\(\,\mathrm{AB}=6\,\)なので\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,6\,\)ですよ。

さて、ここからはいろいろな方向が出てくると思います。
関数で直線が「直交」するなら、
傾きをかけて\(\,-1\,\)とするのが一般的ではありますが、
でもこれは高校入試ですので解法には想定されていないはずです。
与えられた条件を利用して解いていきましょう。

あまり考えすぎても仕方ないので使う条件をひし形にします。
　\(\hspace{10pt}\mathrm{AD=AB}=\color{red}{6}\)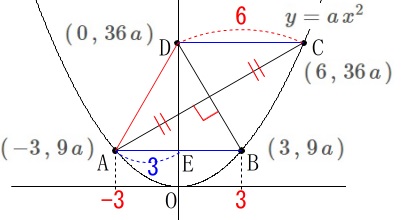線分\(\,\mathrm{AB}\,\)と\(\,y\,\)軸との交点を\(\,\mathrm{E}\,\)とします。

三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AE^2+DE^2}&=&\mathrm{AD^2}\\
3^2+(27\,a)^2&=&6^2\\
27^2\,a^2&=&36-9\\
a^2&=&\frac{1}{27}\\
a&=&\pm \frac{1}{3\sqrt{3}}
\end{eqnarray}\)
\(\,a\,＞\,0\,\)なので
　\(\hspace{10pt}\displaystyle a=\frac{1}{3\sqrt{3}}=\underline{\underline{　\frac{\sqrt{3}}{9}　}}\)

他の考え方が出てきたとしても条件
　\(\,\mathrm{AE=EC}\,\)
　\(\,\mathrm{AC}\,\)⊥\(\,\mathrm{BD}\,\)
を満たしていればそれでいいです。

前半はここまでとさせて頂きます。
学校選択問題を受験する人は高得点を狙っていると思うので、
後半もとれるところは確実にとりましょう。

ただ、ここまでの問題も小問集合とはいえ確実な基礎が必要となりますので、
応用ばかりやる前に確実な基礎を身に付けておくと良いです。

第３問以降の解説

長くなるのでページを分けます。

⇒　令和４年度埼玉県公立高校入試数学【学校選択問題】の解説【後半】

\(\,\large{3}\,\)は座標と確率の条件付き確率で、
一般問題と重複する問題もあります。

\(\,\large{4}\,\)は一般問題と同じですので別解を示すことにします。

\(\,\large{5}\,\)は\(\,5\,\)面体の体積を求める問題があり、
試験時間中に答えまでたどり着けた人は少ないのではないでしょうか。

⇒　埼玉県公立高校入試の数学（一般・学校選択問題）過去問と解説

埼玉県の公立入試は基本中心の一般問題でも年度によってクセがあります。
問題に安定感がないという印象がありますね。