令和４年度埼玉県公立高校入試数学【学校選択問題】の解説【後半】

令和４年（２０２２年）度埼玉県公立高校入試数学【学校選択問題】後半の解説です。
【後半】は第３問第４問第５問としています。
一般入試問題との重複がありますので省略する部分がありますが、
別解を示しておきますので参考にしてください。
どちらが正解ということはなく、方向がちょっと違うだけなので気にしなくていいですよ。

２０２２（令和４年）度埼玉県公立高校入試の数学【学校選択】の問題

試験での注意点は例年通りです。

⇒　２０２２（令和４年）度埼玉県公立高校入試の数学【学校選択】の問題【後半】

後半の問題は\(\,\large{3}\,\)から\(\,\large{5}\,\)までです。
全体が見たい方は【前半】に問題全体があります。
リンクを下に貼っておきますのでご利用ください。

２０２２年度埼玉県公立高校入試の数学【学校選択問題】の解説【後半】

一般問題と重なる部分は省略するか別解としますので、
省略部分は一般問題で確認してください。

第３問格子点と条件付き確率

\(\,\large{3}\,\)
さいころ２つの出目と座標上の格子点と確率です。
図形的性質を取り入れた応用？となりますので直感的でも良いです。
何せ文字が多いので数学らしいシンプルさはありません。

問題の条件は問題文の通りです。
さいころを２回投げて、
１回目を\(\,s\,\)、２回目を\(\,t\,\)とし、
この座標\((\,s\,,\,t\,)\,\)を点\(\,\mathrm{P}\,\)とします。
２点\(\,\mathrm{A\,,\,B}\,\)は
　\(\,\mathrm{A\,(\,2\,,\,1\,)\,,\,B\,(\,4\,,\,5\,)}\,\)点\(\,\mathrm{P}\,\)が存在できるのは\(\,\mathrm{A\,,\,B}\,\)と\(\,●\,\)だけです。

(1)
\(\,\mathrm{∠APB=90^{\circ}}\,\)となる確率を求めます。
「\(\,\mathrm{△APB}\,\)が直角三角形になるとき」ではありません。
（\(\,\mathrm{∠PBA=90^{\circ}}\,\)は考えなくて良いということです。）

円周角の定理から\(\,\mathrm{AB}\,\)を直径とする
円周上に\(\,\mathrm{P}\,\)があれば良いということですね。
ただし、\(\,\mathrm{A\,,\,B}\,\)上にあるときはダメです。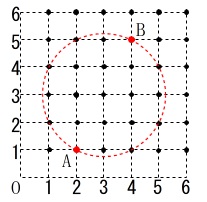直感的に６点あるので確率は
　\(\hspace{10pt}\displaystyle \frac{6}{36}=\underline{\underline{　\frac{1}{6}　}}\)

正確には２点間の距離で三平方の定理が成り立つかどうかで確認します。
コンパスを持っているはずなので円を描いて、
\(\,(\,3\,,\,3\,)\,\)中心の円より内側も外側もダメなので６点を調べれば良いのです。
（\(\,(\,2\,,\,5\,)\,,\,(\,4\,,\,1\,)\,\)はすぐに見つかるので確認から除外できます。）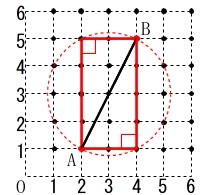

(2)(3)

(2)は間違えることは無いでしょうけど、
(3)は試験中だと焦って間違えても仕方ない、としておきましょう。笑

説明が必要な(3)は条件付き確率で、
問題の注意を読んでいないと間違えます。
一般入試と同じことを書いても仕方ないのでここでの説明は省略します。

⇒　令和４年（２０２２）度埼玉県公立高校入試数学【一般問題】の解説

一般問題の第３問と同じです。

ちょっと補足しておくと、
条件付き確率は公式がありますがベン図で見るとわかりやすいです。\(\,\mathrm{A}\,\)という条件の下で、\(\,\mathrm{B}\,\)である確率は
　\(\hspace{10pt}\displaystyle \frac{　\mathrm{C}\,である確率　}{　\mathrm{A}\,である確率　}\)
となります。
（ここでは\(\,\mathrm{B}\,\)となる『面積が４以上』は\(\,\mathrm{A}\,\)である『三角形である』に内包されますけどね。）

ただ、今は分からなくて良いです。
高校で勉強するときベン図ではそういう意味か、と思い出してください。
（忘れていると思います。笑）

第４問２つの円と共通接線

\(\,\large{4}\,\)
円と接線の問題で一般問題と同じです。

(1)
合同の証明なので省略します。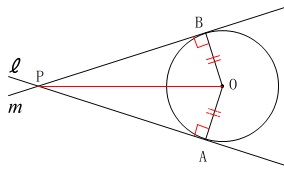合同条件５つは必ず覚えておきましょう。
ここでは「直角三角形の斜辺と他の１辺がそれぞれ等しい。」が合同条件です。

合同や相似の証明の書き方は決まりはありませんので、
自分で形を決めておくと良いですよ。

⇒　中学２年 平行と合同と証明の書き方ポイントまとめ

ポイントは図の中で終わらせておく、です。

(2)
一般問題の解説では相似と三平方の定理を使って求めました。
こちらもそれは変わりませんが一般問題の解説で少し触れた、
２円が接するときに普通に使う平行線を引く方法で求めておきますね。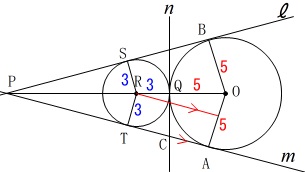中心\(\,\mathrm{R}\,\)から平行線を引いて長方形を作ります。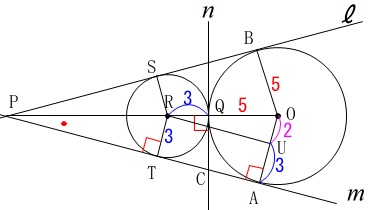点\(\,\mathrm{U}\,\)は\(\,\mathrm{RU}\,\)∥\(\,\mathrm{TA}\,\)となる点で、
　\(\hspace{4pt}\mathrm{OU}=\color{magenta}{2}\,,\,\mathrm{UA}=\color{blue}{3}\,\)
に分けます。
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{OR^2}&=&\mathrm{OU^2+RU^2}\\
(\color{blue}{3}+\color{red}{5})^2&=&\color{magenta}{2}^2+\mathrm{RU^2}\\
\mathrm{RU^2}&=&60
\end{eqnarray}\)
これから
　\(\hspace{4pt}\mathrm{RU}=\mathrm{TA}=\color{red}{2\sqrt{15}}　\)

また\(\,\mathrm{△ROU}\,\)∽\(\,\mathrm{△POA}\,\)から
　\(\hspace{4pt}\mathrm{PR}=\color{magenta}{12}\)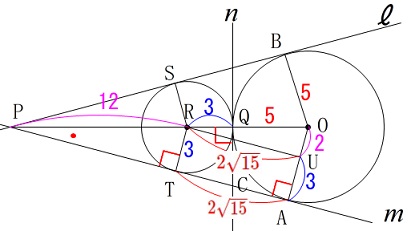（\(\,\mathrm{PR}\,\)については一般問題の解説を参照してください。）

ここからはまた方法が分かれると思いますが、
　\(\hspace{4pt}\mathrm{TC=QC=AC}=\color{red}{\sqrt{15}}\)を利用しておきます。
\(\,\mathrm{△ROU}\,\)∽\(\,\mathrm{△POA}\,\)の相似比が\(\,2:5\,\)なので
　\(\hspace{4pt}\mathrm{PA}=\color{blue}{5\sqrt{15}}\)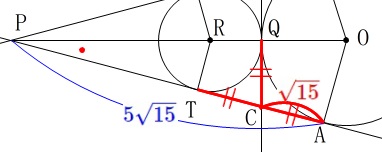よって、
　\(\hspace{10pt}\mathrm{PC}=\underline{　4\sqrt{15}　(\,\mathrm{cm}\,)　}\)

\(\,\mathrm{△PQC}\,\)を使っても良いですが、
今回はあっさりとこれで終わりにします。

第５問立体図形問題

\(\,\large{5}\,\)
体積を３つ求めます。

(1)
立体\(\,\mathrm{V}\,\)は球を半分の半分の半分にしています。
つまり球の体積の\(\,\displaystyle \frac{1}{8}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{4\,\pi}{3}\times (\,r\,)^3\times \frac{1}{8}\\
&=&\underline{\underline{　\frac{\,\pi}{6}\,r^3　}}
\end{eqnarray}\)

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

球の体積を求める公式は中学生では導く事はできませんので、
覚えておかないと使えません。

(2)
四角錐の体積を求めます。
問題文の条件の読み取りは自分でやっておいてください。

底面は四角形\(\,\mathrm{OBDC}\,\)で高さは\(\,\mathrm{AO}\,\)です。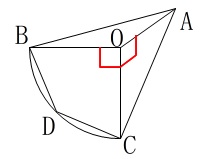点\(\,\mathrm{D}\,\)は弧\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BC}} }\,\)を２等分しているので
　\(\hspace{4pt}\mathrm{∠BOD=∠COD}=45^{\circ}\)
点\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)から線分\(\,\mathrm{OD}\,\)に垂線を下ろすと面積が求まります。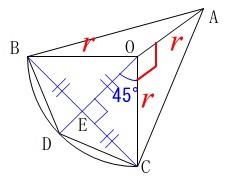見えてきたでしょう。
交点を\(\,\mathrm{E}\,\)とすると\(\,\mathrm{△OBE}\,\)と\(\,\mathrm{△OCE}\,\)直角二等辺三角形で合同です。

三角定規の比で\(\,\mathrm{OB:OE=\sqrt{2}:1}\,\)から
　\(\hspace{10pt}\displaystyle \mathrm{OE=BE=CE}=\color{blue}{\frac{\sqrt{2}}{2}\,r}\)
線分\(\,\mathrm{OD}\,\)は半径だから\(\,\color{red}{r}\,\)なので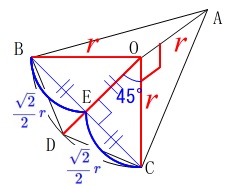　\(\begin{eqnarray}\displaystyle
(\,底面\,\mathrm{OBDC}\,)&=&\frac{1}{2}\times r\times \frac{\sqrt{2}}{2}\,r\times 2\\
&=&\frac{\sqrt{2}}{2}\,r^2
\end{eqnarray}\)
高さは\(\,\color{red}{r}\,\)の錐体なので求める体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \frac{\sqrt{2}}{2}\,r^2\times r\\
&=&\underline{\underline{　\frac{\sqrt{2}}{6}\,r^3　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

ここでは底面積の計算を結果までしていますが、
約分できる可能性があるので高さをかけた後でまとめてでも良いですよ。

面\(\,\mathrm{AOD}\,\)で四角錐が２等分されるので、
三角錐\(\,\mathrm{A-OBD}\,\)の体積を２倍しても良いです。
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \frac{1}{2}\times r\times \frac{\sqrt{2}}{2}\,r \times r \times 2\\
&=&\frac{\sqrt{2}}{6}\,r^3　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

(3)
求めたい５面体の体積は公式で直接は求まりません。
こういう場合の体積は
『部分＋部分』または『全体－部分』ですね。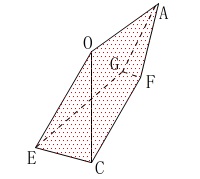球が元にありますが、
面でスパスパ切った５面体なので円周率は関係なくなります。

ところでこの問題の底面の１つと見られる\(\,\mathrm{△OEC}\,\)は、
円に内接する正十二角形の一部で辺の長さや面積が大学入試で取り上げられる事があります。
（外接する正十二面体の場合はもっとややこしい。）

高校数学の基礎というより大学入試の基礎なので、
体積問題に組み込んだこの問題は高校入試で扱うには不適切だと判断しました。
合否判定の参考にならないでしょう。

なので解説は詳しくはしません。
会員向け、しかも『超え太郎』まで目を通している人に向けての解説とします。

ただ、
\(\,\mathrm{△OEC}\,\)の面積は求められるようになっておきたいので、
部分的に少し説明しておきます。

全体の流れとしては次のようになります。
底面は\(\,\mathrm{△OEC}\,\)で、
高さは\(\,\mathrm{OA}\,\)が底面に垂直に立っているのでこれを高さとして利用します。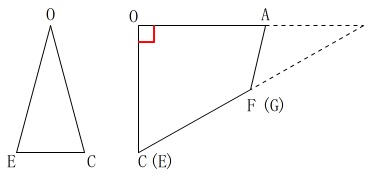真横から見ると\(\,\mathrm{C\,,\,E}\,\)および\(\,\mathrm{F\,,\,G}\,\)は重なるので、
\(\,\mathrm{C\,,\,F}\,\)と、\(\,\mathrm{E\,,\,G}\,\)を延長して\(\,\mathrm{OA}\,\)と交わる点を\(\,\mathrm{P}\,\)とします。
※
３直線は点\(\,\mathrm{P}\,\)で交わります。
イメージだけでもしておいてください。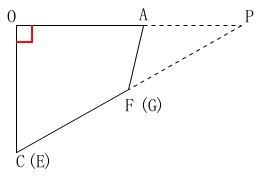全体としての高さは\(\,\mathrm{OP}\,\)です。

つまり、
底面\(\,\mathrm{△OEC}\,\)で高さが\(\,\mathrm{OP}\,\)の三角錐を圧縮して求めるということです。
点\(\,\mathrm{F}\,\)から直線\(\,\mathrm{OA}\,\)に垂線を引いて交点を\(\,\mathrm{Q}\,\)とすると、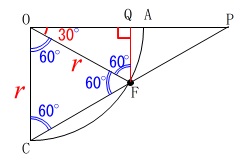三角定規や正三角形からも分かるように
　\(\hspace{10pt}\displaystyle \mathrm{FQ}=\color{red}{\frac{1}{2}\,r}\,,\,\mathrm{OQ}=\color{blue}{\frac{\sqrt{3}}{2}\,r}\)
合同から\(\,\mathrm{PQ=OQ}\,\)なので
　\(\hspace{10pt}\displaystyle \mathrm{OP}=\color{magenta}{\sqrt{3}\,r}\)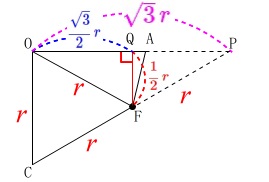高さが出たので底面積を求めましょう。

今回は求められるようになるのはここだけでも良いです。
底面と見なせる\(\,\mathrm{△OEC}\,\)の面積ですね。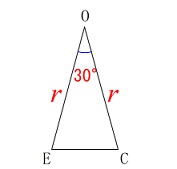\(\,\mathrm{C}\,\)または\(\,\mathrm{E}\,\)から垂線を引きます。
ここでは\(\,\mathrm{E}\,\)から\(\,\mathrm{OC}\,\)に垂線を引きます。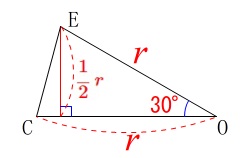三角定規の比から高さが求まるので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△OEC}&=&\frac{1}{2}\times r\times \frac{1}{2}\,r\\
&=&\frac{1}{4}\,r^2
\end{eqnarray}\)

ここまではできるようになっておきましょう。
高校の数学で三角比を使うとすぐに求まりますが、
この垂線を補助線とする方法は覚えておきましょう。

さて、答えを出しておきます。

全体の三角錐\(\,\mathrm{P-OCE}\,\)の体積は
　\(\begin{eqnarray}\displaystyle
\mathrm{(\,P-OCE\,)}&=&\frac{1}{3}\times \mathrm{△OCE}\times \mathrm{OP}\\
&=&\frac{1}{3}\times \frac{1}{4}\,r^2\times \sqrt{3}\,r\\
&=&\color{red}{\frac{\sqrt{3}}{12}\,r^3}
\end{eqnarray}\)
これから部分となる三角錐\(\,\mathrm{P-AFG}\,\)の体積を引きます。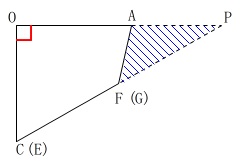
三角錐\(\,\mathrm{P-AFG}\,\)の体積は、
　\(\begin{eqnarray}\displaystyle
\mathrm{PA}&=&\mathrm{OP-OA}\\
&=&\sqrt{3}\,r-r\\
&=&\color{blue}{(\,\sqrt{3}-1\,)\,r}
\end{eqnarray}\)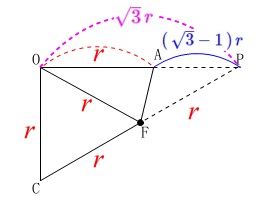また
　\(\hspace{10pt}\displaystyle \mathrm{PF}=\frac{1}{2}\,\mathrm{PC}\,,\, \mathrm{PG}=\frac{1}{2}\,\mathrm{PE}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{(\,P-AFG\,)}&=&\mathrm{(\,P-OCE\,)}\times \mathrm{\frac{PA}{OP}}\times \mathrm{\frac{PF}{PC}}\times \mathrm{\frac{PG}{PE}}\\
&=&\frac{\sqrt{3}}{12}\,r^3 \times \frac{\sqrt{3}-1}{\sqrt{3}}\times \frac{1}{2}\times \frac{1}{2}\\
&=&\color{blue}{\frac{\sqrt{3}}{12}\,r^3 \times \frac{\sqrt{3}-1}{4\sqrt{3}}}
\end{eqnarray}\)
※
ここは『超え太郎』立体図形で確認しておいてください。

よって、求める体積を\(\,V_3\,\)とすると
　\(\begin{eqnarray}\displaystyle
V_3&=&\color{red}{\frac{\sqrt{3}}{12}\,r^3}-\color{blue}{\frac{\sqrt{3}}{12}\,r^3 \times \frac{\sqrt{3}-1}{4\sqrt{3}}}\\
&=&\frac{\sqrt{3}}{12}\,r^3\,\left(\,1-\frac{\sqrt{3}-1}{4\sqrt{3}}\,\right)\\
&=&\frac{\sqrt{3}}{12}\,r^3\times \frac{4\sqrt{3}-\sqrt{3}+1}{4\sqrt{3}}\\
&=&\frac{\sqrt{3}}{12}\,r^3\times \frac{3\sqrt{3}+1}{4\sqrt{3}}\\
&=&\underline{\underline{　\frac{3\sqrt{3}+1}{48}\,r^3　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

計算過程は三角錐\(\,\mathrm{\,P-AFG\,}\,\)の体積を
　\(\hspace{4pt}\displaystyle \mathrm{(\,P-AFG\,)}=\color{magenta}{\frac{\sqrt{3}-1}{48}\,r^3}\)
と計算しておいて
　\(\begin{eqnarray}\displaystyle
V_3&=&\color{red}{\frac{\sqrt{3}}{12}\,r^3}-\color{magenta}{\frac{\sqrt{3}-1}{48}\,r^3}\\
&=&\frac{4\sqrt{3}-\sqrt{3}+1}{48}\,r^3\\
&=&\frac{3\sqrt{3}+1}{48}\,r^3
\end{eqnarray}\)
でも同じです。
　\(\begin{eqnarray}\displaystyle
V_3&=&\color{red}{\frac{\sqrt{3}}{12}\,r^3}\times \left(\,1-\frac{\sqrt{3}-1}{\sqrt{3}}\times \frac{1}{2}\times \frac{1}{2}\,\right)\\
&=&\underline{\underline{　\frac{3\sqrt{3}+1}{48}\,r^3　}}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
とするのが一番スマートに見えますが、
解説が結構手抜きな上に計算まで飛んだら、
分かり難さ１００倍になると思って分けました。　

ところで、
この体積を『部分＋部分』で見る場合ですが、
　\(\,\mathrm{△OCE}\,\)　∽　\(\,\mathrm{△QFG}\,\)
が相似比\(\,2:1\,\)で成り立っていることが分かれば、
なんとか求められると思うのでやってみてください。
錐台と三角錐とみるとすっきり？でもありませんね。

他にも立体を分ける方法はありますが、
入試問題の解説としてはやりたくないので省略します。
立体の体積を求める方法を探る事が目的なのか、
計算処理能力を確かめる事が目的なのか、
両方かもしれませんが試験時間を考えて作られた問題とは思えないので解説をやめます。

以上です。

前半から見直しておきましょう。
実際の試験では時間配分が重要になります。

⇒　令和４年度埼玉県公立高校入試数学【学校選択問題】の解説【前半】

超手抜きの解説で申し訳無いですが、
ここは対策ではないので以上です。

⇒　埼玉県公立高校入試の数学（一般・学校選択問題）過去問と解説

過去２年分は普通に良い問題だと感じるので復習しておくと良いですよ。