令和４年（２０２２）度埼玉県公立高校入試数学【一般問題】の解説

２０２２年（令和４年）度の埼玉県公立高校入試数学の一般問題の解説です。
学校選択問題と重なる問題もありますが、
基本確認問題が主となりますのでミスの無いよう見直し重視で取り組むと良いです。
もちろん、基本をしっかりとおさえておくことが優先です。

２０２２（令和４年）度埼玉県公立高校入試の数学【一般】の問題

試験での注意点は例年通りですが、
ここでも載せておきますので受験の際は同じ内容か確認して開始しましょう。

⇒　2022（令和4年）度埼玉県公立高校入試の数学【一般】の問題

問題は\(\,\large{1}\,\)から\(\,\large{4}\,\)まであります。

２０２２年度埼玉県公立高校入試の数学【一般】問題の解説

早速解説に入ります。

一般問題は十分満点が狙えます。
今は数学は苦手だと感じている人も『覚え太郎』使ってみてください。

⇒　『覚え太郎』ここから入試問題は作られます。

数学が苦手なのでは無く、
今までやってきた方法が違っていたということに気がつきます。

ここでは会員向け解説として簡単に進めます。（予定です。）
試験時間は\(\,50\,\)分あるので試験の受け方を『最大得点法』で確認しておいてください。

第１問計算主体の小問集合

\(\,\large{1}\,\)

(1)
文字式の計算です。
　\(\hspace{10pt}7x-9x\\
=\underline{　-2x　}\)

同類項では係数をまとめるだけです。

(2)
正の数負の数の計算です。
　\(\hspace{10pt}5\times (-3)-(-2)\\
=-15+2\\
=\underline{　-13　}\)

掛け算部分が先ですよ。

(3)
文字式の計算です。
　\(\hspace{10pt}\displaystyle 12x^2y\div 3x\times 2y\\
\displaystyle =\frac{12x^2y\times 2y}{3x}\\
\displaystyle =\underline{\underline{　8\,x\,y^2　}}\)

割り算を逆数の掛け算とするのと、
割る（\(\,\div\,\)）の直後を分母に持ってくるのとは同じことです。

(4)
１次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
7x-2&=&x+1\\
7x-x&=&2+1\\
6x&=&3\\
x&=&\underline{\underline{　\frac{1}{2}　}}
\end{eqnarray}\)

方程式を解くときの基本は全ての項を左辺に集めることですが、
１次方程式では定数項を右辺に持ってきます。
解を求める最終段階にあるからです。

(5)
無理数（根号）の計算です。
　\(\hspace{10pt}\displaystyle \frac{12}{\sqrt{6}}-3\sqrt{6}\\
\displaystyle =\frac{12\sqrt{6}}{6}-3\sqrt{6}\\
=2\sqrt{6}-3\sqrt{6}\\
=\underline{　-\sqrt{6}　}\)

分母の有理化は慣れの段階によって差が出ますが、
ていねいにやっておいた方が良いですね。
こんなところでのミスはもったいないです。

(6)
因数分解です。
　\(\hspace{10pt}x^2-x-20\\
=\underline{　(x+4)(x-5)　}\)

暗算しているように見えるでしょうが、
かけて定数項の数値\(\,20\,\)、
　\(\color{black}{\fbox{\(\,1\times 20\,\)}}\)、\(\color{black}{\fbox{\(\,2\times 10\,\)}}\)、\(\color{red}{\fbox{\(\,4\times 5\,\)}}\)
足して\(\,1\,\)次の係数\(\,-1\,\)になる数を
符号を見ながら探しています。

(7)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 4x-3y=10　･･･①\\
\hspace{4pt} 3x+2y=-1　･･･②
\end{cases}\)
係数から見て加減法が早いです。
先ず\(\,①\times2+②\times 3\,\)で\(\,y\,\)を消去します。
　\(\hspace{20pt} 8x-6y=20\\
\underline{　+)\,9x+6y=-3　}\\
\hspace{18pt}17x\hspace{20pt}=17\\
\hspace{50pt}x=1\)
\(\,①②\,\)のどちらにでも良いので戻すと\(\,y\,\)が求まります。
　\(\begin{eqnarray}\displaystyle
3\times (1)+2y&=&-1\\
2y&=&-4\\
y&=&-2
\end{eqnarray}\)
答え　\(\,\underline{　x=1\,,\,y=-2　}\,\)

順番は先ず\(\,x\,\)を消去する、でも良いですよ。
いずれにしても連立方程式は一文字消去が基本です。

(8)
２次方程式を解きます。
　\(\hspace{10pt}2\,x^2-3\,x-3=0\)
タスキガケを試しても良いですが、
今のところ（現行課程では）\(\,x^2\,\)の係数が\(\,1\,\)でないときは解の公式を優先しましょう。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(-3)^2-4\cdot 2\cdot (-3)}}{2\times 2}\\
&=&\frac{3\pm \sqrt{9+24}}{4}\\
&=&\underline{\underline{　\frac{+\pm \sqrt{33}}{4}　}}
\end{eqnarray}\)

解の公式は導けなくても良いですが、
使えるようにはなっておきましょう。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

公式は使えることが先で良いです。

(9)
角度を求めます。
図に条件が書かれていますので図を読み取らないと始まりません。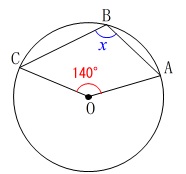\(\,∠x\,\)の中心角は\(\,140°\,\)ではありません。
\(\,\mathrm{∠AOC}=\color{blue}{220°}\,\)側が中心角になります。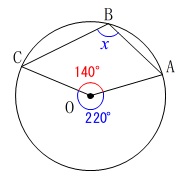\(\hspace{10pt}∠x=\underline{　110^{\circ}　}\)

(10)
１次関数と反比例のグラフがあり、グラフから、
傾きと切片（\(\,y\,\)切片）と反比例の比例定数の符号を読み取ります。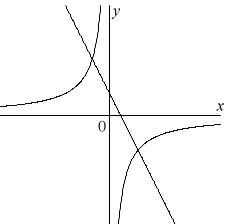それぞれの関数は、
　直線：\(\hspace{4pt}y=a\,x+b\)
　曲線：\(\hspace{4pt}\displaystyle y=\frac{c}{x}\)
です。
先にいっておくと反比例の比例定数は
　\(\hspace{4pt}c=xy\)
から求めることができます。

直線の傾きが右下がりなので\(\hspace{4pt}a\,＜\,0\)
切片が正のところにあるので\(\hspace{4pt}b\,＞\,0\)
反比例のグラフは\(\,x\,\)の値が正のとき\(\,y\,\)の値は負なので
比例定数\(\,c\,\)は　\(\hspace{4pt}c\,＜\,0\)

答え　\(\,\underline{　カ　}\,\)

(11)
おうぎ形の中心角を求めます。
　母線の長さが\(\,8\,\)、底面の円の半径が\(\,3\,\)の円錐
の展開図におけるおうぎ形の中心角です。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。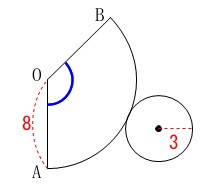比例式で良いですよ。
底面の円の半径が\(\,3\,\)なので、
おうぎ形の弧の長さが一致して\(\hspace{10pt}\color{blue}{6\,\pi}\)
一方、母線がおうぎ形の半径になります。
半径\(\,\color{red}{8}\,\)の円周の長さは\(\,\color{magenta}{16\,\pi}\,\)なので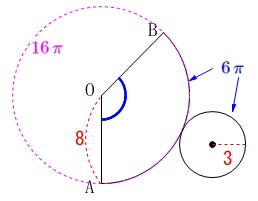中心角は弧の長さに比例するから
　\(\begin{eqnarray}\displaystyle
\color{magenta}{16\,\pi}:\color{blue}{6\pi}&=&360^{\circ}:∠\mathrm{AOB}\\
∠\mathrm{AOB}&=&\frac{6\,\pi}{16\,\pi}\times 360^{\circ}\\
&=&\frac{3}{8}\times 360^{\circ}\\
&=&\underline{　135^{\circ}　}
\end{eqnarray}\)

⇒　1次方程式と比例式の利用と解き方のまとめ

比例式は相似でも大いに利用します。
使えるようにしておくと良いです。

比例式に慣れている会員は
　\(\begin{eqnarray}\displaystyle
16\,\pi\times \frac{\mathrm{∠AOB}}{360°}&=&6\,\pi\\
\mathrm{∠AOB}&=&360^{\circ}\times \frac{6}{16}\\
&=&\underline{　135^{\circ}　}
\end{eqnarray}\)

と計算したと思いますが、
理科でもよく使う比例の関係式なので良いですね。

⇒　比例式の応用文章題への利用と便利な比の使い方

他ではお目にかかれない比例計算方法です。

(12)
ルートの付いた数が整数になる自然数\(\,n\,\)が何通りあるか求めます。
　\(\hspace{10pt}\displaystyle \sqrt{\frac{540}{n}}\rightarrow 整数\)

全体が整数となるので分子が\(\,n\,\)で割り切れ、
さらに残りが平方数となる場合です。
　\(\hspace{10pt}540=2^2\times 3^3\times 5=2^2\times 3^2\times \color{red}{3\times 5}\)
なので\(\,n\,\)は\(\,3\times 5\,\)を必ず持っていて、
　\(\hspace{10pt}\color{red}{3\times 5}\,,\,\color{red}{3\times 5}\times 2^2\,,\,\color{red}{3\times 5}\times 3^2\,,\,\color{red}{3\times 5}\times 2^2\times 3^2\)
の場合に全体が整数になります。

答え　\(\,\underline{　4\,通り　}\,\)

ルートの付いた数は素因数分解して見ることが基本ですね。
※
素因数分解は必ず自分でやって確認しておきましょう。

(13)
平行線で作られた相似の問題です。
条件（長さの単位は\(\,\mathrm{cm}\,\)です。）
　\(\,\mathrm{ＡＢ}\,\)∥\(\,\mathrm{ＣＤ}\,\)∥\(\,\mathrm{ＥＦ}\,\)
　\(\,\mathrm{AB=2\,,\,DC=3}\,\)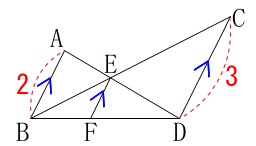平行線があるので同位角や錯角が等しいから、
相似な三角形がいろいろあるので書き出しておくと良いですよ。

先ずは\(\,\mathrm{AB=2\,,\,DC=3}\,\)を含んだ相似です。
平行線の錯角が等しくなるので
　\(\,\mathrm{△EAB}\,\)　∽　\(\,\mathrm{△EDC}\,\)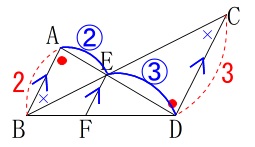相似比は\(\,\color{red}{2}:\color{red}{3}\,\)です。

また平行線の同位角は等しいので
　\(\,\mathrm{△DAB}\,\)　∽　\(\,\mathrm{△DEF}\,\)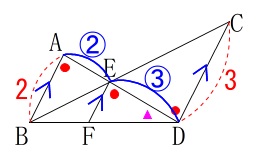相似比は
　\(\hspace{4pt}\mathrm{AD:ED}=(2+3)：3\,=\,5:3\,\)
となるので
　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\mathrm{AB}\times \frac{3}{5}\\
&=&2\times \frac{3}{5}\\
&=&\underline{\underline{　\frac{6}{5}　}}(\,\mathrm{cm}\,)
\end{eqnarray}\)

もちろん比例式を利用しても良いです。
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:ED}&=&\mathrm{AB:EF}\\
5:3&=&2:\mathrm{EF}\\
5\times \mathrm{EF}&=&3\times 2\\
\mathrm{EF}&=&\frac{6}{5}
\end{eqnarray}\)

どちらかというと比例式の方が機械的に進められますが、
やっていることは同じです。

または、\(\,\mathrm{△BEF}\,\)∽\(\,\mathrm{△BCD}\,\)でもあるので
（相似比は\(\,2:5\,\)です。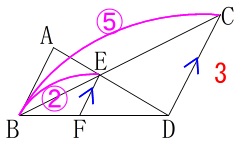）　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\frac{2}{5}\times \mathrm{DC}\\
&=&\frac{2}{5}\times 3=\frac{6}{5}
\end{eqnarray}\)
でも同じです。

(14)
箱ひげ図について誤っているものを一つ選びます。

中央値と平均値は違います。

答え　\(\,\underline{　ウ　}\,\)

他は正しいです。

(15)
標本調査です。

比例関係を利用した推測値なので比例式ですね。
養殖池の魚の総数を\(\,x\,\)とします。
その中の\(\,22\,\)匹に印をつけて戻しています。
数日後（魚は増えたり減ったりしていないとして）
\(\,23\,\)匹捕獲した中に印のついた魚が\(\,3\,\)匹であるときなので
　\(\begin{eqnarray}\displaystyle
23:3&=&x:22\\
3\,x&=&23\times 22\\
x&=&\frac{23\times 22}{3}\\
&=&168.66\cdots
\end{eqnarray}\)

答え　およそ\(\,\underline{　169　}\,\)匹

魚の総数と印をつけた魚の比と、
捕獲した魚と印のついた魚の比が同じ、という比例関係です。

(16)
相似と体積比から割安なサイズを求める問題です。

相似比が\(\,a:b\,\)のとき体積比は\(\,a^3:b^3\,\)ですが、
ここでは相似だけではないので３つのサイズの体積比を出します。

\(\,\mathrm{S}\,\)と\(\,\mathrm{M}\,\)は相似で相似比\(\,3:4\,\)なので体積比は
　\(\hspace{10pt}\mathrm{S:\color{red}{M}}=27:\color{red}{64}\)
\(\,\mathrm{M}\,\)と\(\,\mathrm{L}\,\)の底面は相似で相似比\(\,4:5\,\)、
高さの比は\(\,1:2\,\)なので体積比は
　\(\begin{eqnarray}\displaystyle
\mathrm{M:L}&=&4^2\times 1:5^2\times 2\\
&=&16:50
\end{eqnarray}\)
ここで３つのサイズを比較するため\(\,\mathrm{M\,,\,L}\,\)の比を４倍します。
（\(\,\mathrm{M}\,\)の比を同じ数値にするためです。）
　\(\hspace{10pt}\mathrm{\color{red}{M}:L}=\color{red}{64}:200\)

体積比は
　\(\hspace{10pt}\mathrm{S:M:L}=27:\color{red}{64}:200\)
これを価格と照らし合わせます。
　\(\begin{array}{|c|c|c|c|} \hline
　サイズ　 & \mathrm{S} & \mathrm{M} & \mathrm{L} \\ \hline
価格 & \,160\, & \,320\, & \,960\, \\ \hline
体積比 & 27 & 64 & 200 \\ \hline
\end{array}\)
比較の方法は価格を体積比で割っても良いですし、
価格の比が\(\,1:2:6\,\)になっているので体積比を見比べても良いです。

\(\,\mathrm{S}\,\)を基準に見ると\(\,\mathrm{M}\,\)は価格が\(\,2\,\)倍、
体積は\(\,2\,\)倍以上あるので\(\,\mathrm{M}\,\)の方が割安で、
\(\,\mathrm{M}\,\)を基準に見ると\(\,\mathrm{L}\,\)は価格が\(\,3\,\)倍で、
体積は\(\,3\,\)倍以上あるので\(\,\mathrm{L}\,\)の方が割安です。

答え　\(\,\underline{　\mathrm{L}　}\,\)　サイズ

市場ではサイズが大きければ割安になることが多いですが、
たまにだましの価格があるので注意しておきましょう。笑

\(\,\large{1}\,\)は以上です。

第２問作図とグラフ上の面積

\(\,\large{2}\,\)
作図と座標上の平行四辺形の面積を求める２題があります。
（必然的に比例定数を求めますがそれも問題になっています。）

(1)
おうぎ形の中心角が\(\,180°\,\)は半円です。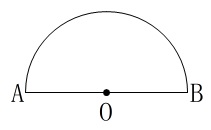弧\(\,\stackrel{\large{\frown}}{\mbox{AB}}\,\)上に
　\(\,\mathrm{AO:AC=1:\sqrt{2}}\,\)
となる点\(\,\mathrm{C}\,\)を作図します。
　\(\,\mathrm{∠AOC=90°}\,\)
となるとき\(\,\mathrm{△AOC}\,\)は直角二等辺三角形になるので
　\(\,\mathrm{AO:AC=1:\sqrt{2}}\,\)
となります。

手順は\(\,\mathrm{O}\,\)を通り\(\,\mathrm{AB}\,\)に垂線を引いて、
弧\(\,\stackrel{\large{\frown}}{\mbox{AB}}\,\)との交点を\(\,\mathrm{C}\,\)とします。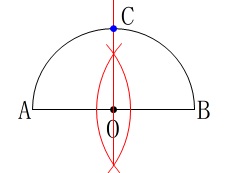比でも\(\,\sqrt{2}\,\)の長さを作りたい場合は直角二等辺三角形ですね。※
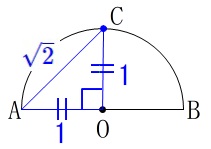会員の方は\(\,\color{blue}{1}:\color{blue}{\sqrt{2}}\,\)の長さの取り方は
作図問題集『さくっと！』（問題\(\,22\,\)）の解説中にありますので確認しておきましょう。

(2)
条件を整理して図の中で処理すればすぐに終わります。

条件
　曲線の関数：\(\,y=a\,x^2\,(\,a\,＞\,0\,)\)
　\(\,\mathrm{A\,,\,B\,,\,C}\,\)は曲線上の点。
　\(\,\mathrm{D}\,\)は\(\,y\,\)軸上の点で\(\,y\,\)座標が\(\,\mathrm{C}\,\)と等しい。
　\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標はそれぞれ\(\,-3\,,\,3\,\)
　点\(\,\mathrm{D}\,\)の\(\,y\,\)座標は\(\,8\,\)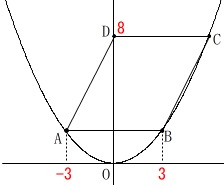四角形\(\,\mathrm{ABCD}\,\)が平行四辺形なので
　\(\,\mathrm{AB=DC=6}\,\)
だから点\(\,\mathrm{C}\,\)の座標は\(\,\color{blue}{(\,6\,,\,8\,)}\,\)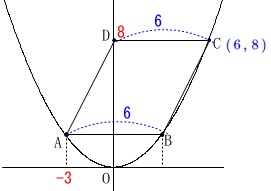点\(\,\mathrm{C}\,\)を通るので関数の比例定数は
　\(\begin{eqnarray}\displaystyle
\color{blue}{8}&=&a\times (\,\color{blue}{6}\,)^2\\
a&=&\underline{\underline{　\frac{2}{9}　}}
\end{eqnarray}\)

平行四辺形の面積は底辺\(\,\mathrm{AB}\,\)、
高さは\(\,\mathrm{A\,,\,B}\,\)の\(\,y\,\)座標と\(\,\mathrm{C\,,\,D}\,\)の\(\,y\,\)座標の差です。
曲線の関数\(\hspace{4pt}\displaystyle y=\frac{2}{9}\,x^2\,\)において\(\,x=3\,\)から
　\(\begin{eqnarray}\displaystyle
y&=&\frac{2}{9}\times (3)^2\\
&=&2
\end{eqnarray}\)
\(\,\mathrm{A\,,\,B}\,\)の\(\,y\,\)座標は\(\,2\,\)となります。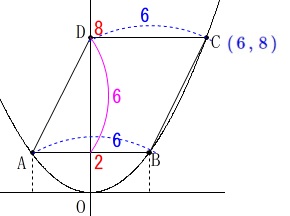よって平行四辺形の高さは\(\,\color{magenta}{6}\,\)となるので求める面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&6\times 6\\
&=&\underline{　36　}(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

説明をみると長く感じるかもしれませんが、
分かる条件をグラフ上に書き込んで行けばすぐに終わりますよ。

\(\,\large{2}\,\)は以上です。

第３問座標と確率の融合問題

\(\,\large{3}\,\)
さいころ２つの確率ですが、
求める確率に条件がつきます。

設定
　座標上に\(\,\mathrm{A\,(\,2\,,\,1\,)\,,\,B\,(\,4\,,\,5\,)}\,\)がある。
　さいころを２回投げ１回目を\(\,s\,\)、２回目を\(\,t\,\)とする。
　座標\(\,(\,s\,,\,t\,)\,\)を点\(\,\mathrm{P}\,\)とする。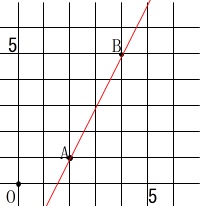直線\(\,\mathrm{AB}\,\)上に\(\,\mathrm{P}\,\)が来るとき三角形になりません。

(1)
直線\(\,\mathrm{AB}\,\)の式を求めます。
２点
　\(\,\mathrm{A\,(\,2\,,\,1\,)}\,\)
　\(\,\mathrm{B\,(\,4\,,\,5\,)}\,\)
を通るので傾きは
　\(\hspace{10pt}\displaystyle \frac{5-1}{4-2}=2\)
求める直線を\(\hspace{4pt}y=2\,x+b\,\)とすると
\(\,\mathrm{A\,,\,B}\,\)を通るのでどちらかを代入して
　\(\begin{eqnarray}\displaystyle
5&=&2\times (4)+b\\
b&=&-3
\end{eqnarray}\)

答え　\(\hspace{10pt}\underline{　y=2\,x-3　}\)

２点を通る直線の式の求め方は慣れておいた方が良いです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い
　
関数総合問題では求める直線が何本も出てくることが多いので、
時間をあまりかけたくありません。

(2)
三角形にならない点\(\,\mathrm{P}\,\)の個数と、
三角形になる点\(\,\mathrm{P}\,\)の個数を求めます。

さいころを２回投げるので出方は全部で３６通り、
三角形になる場合の点\(\,\mathrm{P}\,\)の数は、
三角形にならない個数が分かれば３６から引けば良いのですが、
この問題では条件をつけた確率を求めるので求めておくようにしてあります。
※
条件付き確率は現時点では高校で習います。
この問題では文章に沿って考えるしかありません。点\(\,\mathrm{P}\,\)は青い正方形の中の格子点になります。
（格子点とは\(\,x\,,\,y\,\)座標ともに整数の点です。）

\(\,\mathrm{△ABP}\,\)が三角形にならないのは、
点\(\,\mathrm{P}\,\)が直線\(\,\mathrm{AB}\,\)上にあるときで
　\(\,(\,2\,,\,1\,)\,,\,(\,3\,,\,3\,)\,,\,(\,4\,,\,5\,)\,\)
の３点があります。
答え　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　3　}\,\)

三角形になるのは残りの\(\,33\,\)点になります。
答え　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　33　}\,\)

次に\(\,\mathrm{△ABP}\,\)の面積が\(\,4\,\)以上になるときですが、
計算で出るわけではありません。

調べて行くことで見えてくることがあります。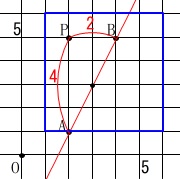おおよそで良いので\(\,\mathrm{△ABP}\,\)の面積が\(\,4\,\)になりそうな点を探していくと、
点\(\,\mathrm{P}\,\)が\(\,(\,2\,,\,5\,)\)のときちょうど\(\,4\,\)になります。
反対側では点\(\,\mathrm{P}\,\)が\(\,(\,4\,,\,1\,)\)のときです。底辺を\(\,\mathrm{AB}\,\)と見ると高さがそれ以上であれば面積が\(\,4\,\)以上になるので
点\(\,(\,2\,,\,5\,)\)を通り\(\,\mathrm{AB}\,\)に平行な直線、
点\(\,(\,4\,,\,1\,)\)を通り\(\,\mathrm{AB}\,\)に平行な直線を境界として、
直線\(\,\mathrm{AB}\,\)から遠い位置にある点が面積\(\,4\,\)以上です。
全部で\(\,15\,\)点あります。

求める確率ですが分母が\(\,36\,\)でないことに注意が必要で、
『三角形となる場合のうち』という条件付きで
　\(\hspace{10pt}\displaystyle \frac{15}{33}=\underline{\underline{　\frac{5}{11}　}}\)

三角形になるのは\(\,36\,\)通りのうち、
\(\,33\,\)通りだったことを忘れないようにしましょう。

この問題は『\(\,\mathrm{△ABP}\,\)の面積が\(\,\mathrm{4}\,\)以上になる確率』であれば、
　\(\hspace{10pt}\displaystyle \frac{15}{36}=\frac{5}{12}\)
という答えになります。

これを間違えてしまった人は今は気にしなくて良いですが、
会話の中で注意点を話しているのでこういう確率を、
『条件付き確率』というんだと覚えておいて高校でしっかり勉強しましょう。

第４問平面図形（円と接線）

\(\,\large{4}\,\)

線分の長さが等しいことの証明と、
線分の長さを求める２問です。

条件として円と接線があります。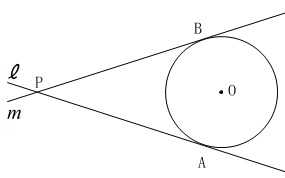２点\(\,\mathrm{A\,,\,B}\,\)は接点、
点\(\,\mathrm{P}\,\)は２本の接線の交点です。

(1)
証明です。
　\(\hspace{4pt}\mathrm{PA＝PB}\)
の証明ですが合同を証明すれば良いだけです。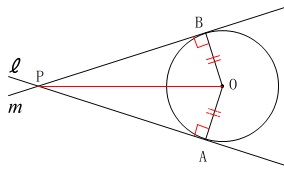合同の証明のポイントは、
図の中で合同条件を集めることです。

⇒　中学２年平行と合同と証明の書き方ポイントまとめ

ここで証明しても意味は無いので、
自分で証明してみてください。

合同条件は『直角三角形の斜辺と他の１辺がそれぞれ等しい。』です。
ただし、合同の証明で終わらないようにしてください。

問題は対応する辺が等しいことの証明ですよ。

(2)
線分の長さを求めますが、もう一つ円が加わります。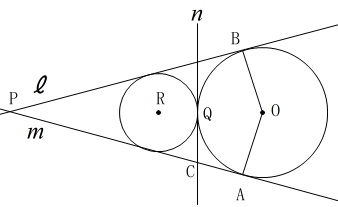条件は問題の通りで見たままです。
長さの条件があります。（単位は\(\,\mathrm{cm}\,\)です。）
　円\(\,\mathrm{O}\,\)の半径が\(\,\color{red}{5}\,\)
　円\(\,\mathrm{R}\,\)の半径が\(\,\color{blue}{3}\,\)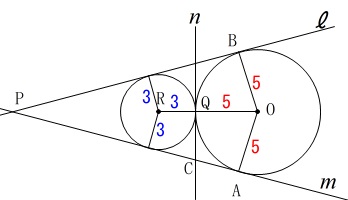このとき\(\,\mathrm{PC}\,\)の長さを求めます。

解答方針の方向性はいろいろありますが、
先ずは分かることから書き込んで行きましょう。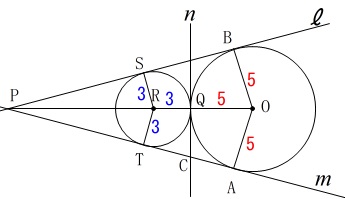(1)で証明した事からも分かるように、
円\(\,\mathrm{R}\,\)と共通の接線との交点を\(\,\mathrm{S\,,\,T}\,\)とすると、
\(\,\mathrm{O\,,\,Q\,,\,R\,,\,P}\,\)は一直線上にあり、
　\(\,\mathrm{△PSR}\,\)　≡　\(\,\mathrm{△PTR}\,\)
　\(\,\mathrm{△PBO}\,\)　≡　\(\,\mathrm{△PAO}\,\)
また
　\(\,n\,\)　⊥　\(\,\mathrm{OP}\,\)
　\(\,\mathrm{OB}\,\)　∥　\(\,\mathrm{RS}\,\)
　\(\,\mathrm{OA}\,\)　∥　\(\,\mathrm{RT}\,\)
でもあります。

この図中での性質は直感的でも良いですよ。
２円が接するときは接点\(\,\mathrm{Q}\,\)は中心\(\,\mathrm{O\,,\,R}\,\)から、
線分\(\,\mathrm{OQ+RQ}\,\)（半径の和）が一番小さくなるときなので一直線になります。
後は\(\,\mathrm{∠BPA}\,\)の二等分線が\(\,\mathrm{OP}\,\)なので合同、相似が見えてきます。

方法はいくつかあります。
２円が接するときよく使う方法は平行線ですが、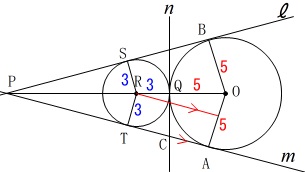相似と三平方の定理の利用で終わらせます。

相似な三角形がたくさんありますので迷うでしょうけど、
いくつか書き出しておくと良いですね。
　\(\,\mathrm{△PRT}\,\)　∽　\(\,\mathrm{△POA}\,\)　∽　\(\,\mathrm{△PCQ}\,\)
相似から\(\,\mathrm{PR}\,\)と三平方の定理で\(\,\mathrm{CQ}\,\)を求めて行きましょう。

\(\,\mathrm{PR}=\color{blue}{x}\,\)とすると、
　\(\hspace{4pt}\mathrm{PO=PR+RO}=x+8\)
なので\(\,\mathrm{△PRT}\,\)　∽　\(\,\mathrm{△POA}\,\)から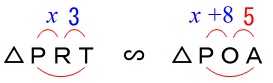　\(\begin{eqnarray}\displaystyle
\mathrm{PR:PO}&=&\mathrm{RT:OA}\\
x:(\,x+8\,)&=&3:5\\
5x&=&3(\,x+8\,)\\
5x&=&3x+24\\
2x&=&24\\
x&=&12
\end{eqnarray}\)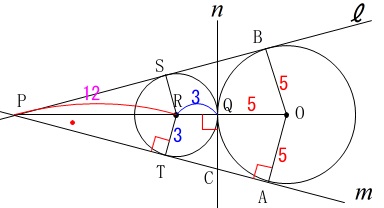このとき三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{PT^2+RT^2}&=&\mathrm{PR^2}\\
\mathrm{PT}^2+3^2&=&12^2\\
\mathrm{PT}^2&=&144-9\\
&=&135\\
\mathrm{PT}&=&\pm 3\sqrt{5}
\end{eqnarray}\)
\(\,\mathrm{PT}\,\)は長さだから\(\,\mathrm{PT}\,＞\,0\,\)で
　\(\hspace{10pt}\mathrm{PT}=\color{magenta}{3\sqrt{5}}\)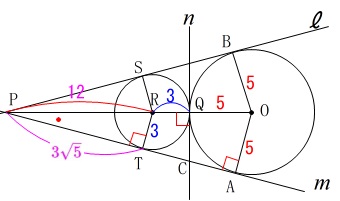さらに
　\(\begin{eqnarray}\displaystyle
\mathrm{PQ}&=&\mathrm{PR+RQ}\\
&=&12+3=15
\end{eqnarray}\)
となるので\(\,\mathrm{△PRT}\,\)∽\(\,\mathrm{△PCQ}\,\)から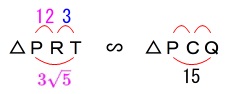
　\(\begin{eqnarray}\displaystyle
\mathrm{PR:PC}&=&\mathrm{PT:PQ}\\
12:\mathrm{PC}&=&3\sqrt{5}:15\\
3\sqrt{5}\times \mathrm{PC}&=&15\times 12\\
\mathrm{PC}&=&\frac{15\times 12}{3\sqrt{5}}\\
&=&\underline{　4\sqrt{5}　}(\,\mathrm{cm}\,)
\end{eqnarray}\)