2018年東京都公立高校入試の前期問題問5空間図形の解説

2018年に東京都で行われた公立高校入試の前期問題問5の解説です。
問5は空間図形の総合問題です。
当然のように最後は体積問題ですが具体的な数値が与えられているので難しくはありません。

⇒　2018東京都立高校入試前期の数学問題

　\(\large{\color{black}{\fbox{ 5 }}}\)

図形問題の最初にすること

\(\,問1\,\)は角度を求める問題ですが、図形問題は平面図形、空間図形関係なく条件を図示することから始めます。
ボーとながめてても何も進みませんよ。

この問題のように「\(\,問1\,\)」に入り前に書いてある条件はすべての問題に共通する条件です。

　\(\,\mathrm{AB=AC=AD}=9\,\)
　\(\,\mathrm{∠BAC=∠BAD=CAD}=90°\,\)
　\(\,\mathrm{M}\,\)は\(\,\mathrm{EF}\,\)の中点

ここまでの条件はすべての問題に共通して使えますが、密かにかくされた条件もあるので書き出しておきます。

\(\,\mathrm{△ABC}\,\)は直角二等辺三角形なので
　\(\,\mathrm{∠ABC=∠ACB}=45°\,\)

これくらいは気がついているでしょうけど、加えておきます。
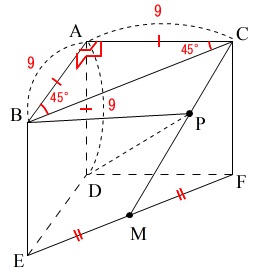三角柱なので他にも等しい辺や角はありますが、見にくくなるのでその都度書くことにします。

条件付きの角度の求め方

〔\(\,問1\,\)〕
点\(\,\mathrm{P}\,\)が\(\,\mathrm{C}\,\)に一致するときの\(\,\mathrm{∠BPD}\,\)の角度を求めます。
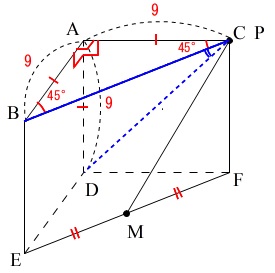空間図形では長さや角度を求めたいとき、求めたい角や辺を含む平面を抜き出します。
ここでは\(\,\mathrm{△BPD}\,\)を抜き出せば良いのです。

\(\,\mathrm{△BPD}\,\)は\(\,3\,\)辺が正方形の対角線になっているので、

　\(\,\mathrm{BP=BD=PD=9\sqrt{2}}\,\)つまり\(\,\mathrm{△BPD}\,\)は正三角形だから

　\(\,\mathrm{∠BPD=\underline{60}}（度）\,\)

線分比と体積の関係

〔\(\,問2\,\)〕点\(\,\mathrm{P}\,\)が移動します。

\(\,\mathrm{CP:PM}\,=2:1\)のときの三角錐の体積です。
立体\(\,\mathrm{P-ABD}\,\)とは\(\,\mathrm{△ABD}\,\)を底面とする三角錐ですよ。
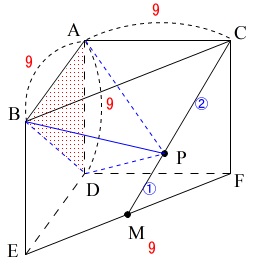底面積は簡単に求まりますが、高さをどうやって求めるか、ですね。

相似を使いますが、\(\,\mathrm{AC}\,\)を基準にして比がわかれば点\(\,\mathrm{P}\,\)の高さも求まります。
しかし、高さを求めるために比を利用するなら、底面積が同じなので体積ごと比を利用するとはやいです。

底面積が同じなので、高さの比が体積の比になるからです。

高さを求めて具体的に体積を求める方法と、
基準の体積から比で体積を求める方法と2つ説明しておきます。

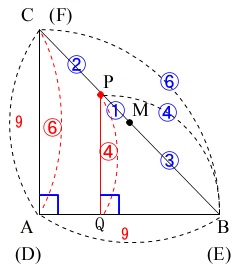
底面積は\(\,\mathrm{△ABD}\,\)なのでみる方向を変えておきます。
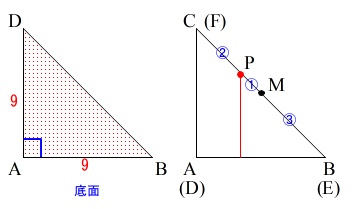左は底面となる三角形\(\,\mathrm{ABC}\,\)、
右は元の立体からすると真上からみた、高さを透過させて見た図になります。
高さは真横から見れば変わりませんので透過させても同じ高さです。

底面積は

　\(\begin{eqnarray}
\displaystyle \mathrm{△ABD}&=&\frac{1}{2}\times 9\times9\\
&=&\frac{81}{2}
\end{eqnarray}\)

ここから高さを具体的に求めて体積を求めるか、
高さの比を出して基準とする体積からの比で体積を求めるかが分かれます。
まずは具体的な長さを出します。
点\(\,\mathrm{P}\,\)から底面の正方形\(\,\mathrm{ABED}\,\)に下ろした垂線との交点を\(\,\mathrm{Q}\,\)とすると

　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△QBP}\,\)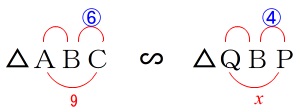
\(\,\mathrm{PQ}=x\,\)として相似な三角形の比を利用すると、

　\(\begin{eqnarray}
\mathrm{BC:BP}&=&\mathrm{AC:QP}\\
6:4&=&9:x\\
6x&=&4\times 9\\
6x&=&36\\
x&=&6　
\end{eqnarray}\)

つまり、三角錐の高さ\(\,\mathrm{PQ}\,\)が\(\,6\,\)で、
立体\(\,\mathrm{P-ABD}\,\)の体積は

　\(\hspace{10pt} \displaystyle \frac{1}{3}\times (底面積)\times (高さ)\\
\displaystyle =\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{PQ}\\
\displaystyle =\frac{1}{3}\times \frac{81}{2}\times 6\\
=\underline{81}
\)

と簡単に求まります。

　・柱体の体積は\(\,\mathrm{底面積×高さ}\,\)であること。
　・錐体の体積が柱体の\(\displaystyle \frac{1}{3}\)であること。
　・相似な三角形から線分比が出てくること。

これらは教科書に基本として書いてあることです。
教科書の範囲で解けない公立入試問題はありません。

「高得点とらなければ」と焦る気持ちも分かりますが、
応用問題ばかり練習する前に『覚え太郎』の復習した方が良いです。

図を書いて分解して、組み立てていく、という作業さえしっかりやれば解けるように問題は作られているし、作業しないと解けないようにもなっています。

　\(\large{\color{magenta}{\fbox{『覚え太郎』×『作業』}}}\)

で、高校入試の数学はほぼ満点に近い得点になりますよ。

⇒　中学数学短期攻略『覚え太郎』

『覚え太郎』をはずして高校入試の問題は作れません。

もう一つの基準体積を比で計算する方法を示しておきます。
これも簡単なのでさっとすませます。

高さとなる比を\(\,\mathrm{CA:PQ}\,\)とします。基準となる体積を三角錐\(\,\mathrm{C-ABD}\,\)とすると、

　\(\hspace{10pt}(三角錐\mathrm{C-ABD}の体積)\\
\displaystyle =\frac{1}{3}\times \mathrm{△ABD}\times \mathrm{CA}\\
\displaystyle =\frac{1}{3}\times \frac{81}{2}\times 9\\
\displaystyle =\frac{243}{2}\)
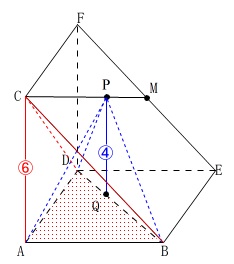立体\(\,\mathrm{P-ABD}\,\)の高さと\(\,\mathrm{C-ABD}\,\)の高さの比は

　\(\,⑥：④=\color{red}{3:2}\,\)

なので立体\(\,\mathrm{C-ABD}\,\)の体積は

　\(\hspace{10pt}(立体\mathrm{C-ABD}の体積)\\
\displaystyle = (立体\mathrm{P-ABD}の体積)\times\color{red}{\frac{2}{3}}\\
\displaystyle =\frac{243}{2}\times \color{red}{\frac{2}{3}}\\
=\underline{81}\)

と求めることもできます。

どちらでも良いです。
実際の試験会場であれこれきれいな解法を考えているヒマはありません。
図に書き込んでみて、気がついた方法で突っ走れば良いですよ。

これで東京2018年前期試験の数学は終了です。

⇒　東京都公立高校入試数学の過去問と解答解説

過去問はあまり対策にはなりませんが傾向だけでも知っておきましょう。