2018年度の大阪府公立入試A問題の数学問3関数と規則性の解説

2018年(平成30年)度の大阪府で行われた公立入試A問題の問3の解説です。
問3は1次関数と規則性の融合ともいえますが問題文の意味を読み取りさえすれば難しくはありません。
問題文が長いですが問題文がいっていることを図示していけば良いだけです。

問題は大阪府の公式サイトにもあります。

⇒　大阪府2018年A数学問題　

文章題が苦手な人は見方を変えてみる

問題文が長いですが余計な日本語が問題を長くしています。
いらないところを消してみるとすっきりすることも多いですよ。

　「Mさん」なんて誰でも良い部分は読み飛ばしてかまいません。
　本でなくても箱でも同じです。
こういう部分を消して、問題文を見てみると日本語の文章が少なくなるので取り組みやすくなる人もいるはずです。

数学の問題文は、国語の文章ではないので大事なところが繰り返されるわけではありません。
条件は一度しか書かれません。
数学の文章にすると短いので日本語で長く見せて、取り組む、という部分で少し難易度を上げているだけですよ。

問題に書いてある条件は、
　横\(\,15\,\mathrm{cm}\,\)、縦\(\,2\,\mathrm{cm}\,\)の長方形を積み重ねたとき、
　周囲の長さ\(\,y\,\)はどうなっていくか？
ということです。

　本の冊数を\(\,x\,\)
　周囲を\(\,y\,\)
とすると、という表がありますが、\(\,1\,\)冊、\(\,2\,\)冊、と増やしていくとどうなるか、という規則性の問題と同じです。

関数もすべて規則性が始まり

(1)
これは表にあてはまる数値を書き込むことになりますが、
(1)に取り組む前に少しでも規則性を見た人なら(2)の関数が先に出ているでしょう。

数学の応用問題では、必ず条件から導き出さなければならない一般性があります。
あまり難しく考えなくて良いですよ。

例えば、
　本\(\,1\,\)冊の場合周囲は　\(2+2+15+15=34\)
　本\(\,2\,\)冊の場合周囲は　\(2\times 2+2\times 2+15+15=38\)
　本\(\,3\,\)冊の場合周囲は　\(2\times 3+2\times 3+15+15=42\)
と、一つひとつ例を出してみて、ある程度一般性を見ておくという作業をするのです。
これができるようになれば公立入試はほぼ全国の問題で満点近くとれますよ。

この場合横の長さは変わらない、縦だけが変わるんだな、と簡単にで良いので規則性を見るのです。

本が一冊増えると一定の数だけ増えているので1次関数だと見抜けば終わりです。

ではなぜ(1)があるのか？

この規則性を見つけるという作業を普通の中学生はしないので、
問題の中で規則性を見てね、と作成者が親切に誘導してくれているのです。

せっかくですので誘導に乗りましょう。
（大学入試を受ける人はセンター試験、共通テストはもちろん本試験でも誘導に乗れないと数学は撃沈しますよ。笑）

改めて、表に当てはまる数を探しましょう。
図を書けばすぐに求まります。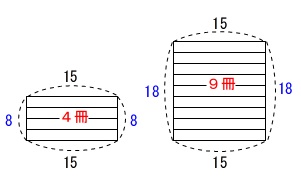
本が\(\,4\,\)冊 \(\,x=4\,\) のとき周囲\(\,y\,\)は　
　\(\begin{eqnarray}
y&=&8+8+15+15\\
&=&\underline{　46　}
\end{eqnarray}\)

本が\(\,9\,\)冊 \(\,x=9\,\) のとき周囲\(\,y\,\)は　
　\(\begin{eqnarray}
y&=&18+18+15+15\\
&=&\underline{　66　}
\end{eqnarray}\)

(2)上の2つを計算するときに気がついていると思います。

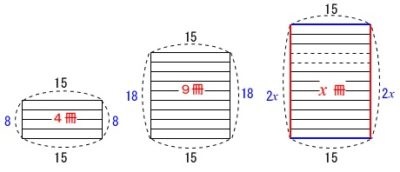
横は一定で\(\,15\mathrm{cm}\,\)、縦が\(\,1\,\)冊\(\,2\mathrm{cm}\,\)で\(\,x\,\)冊のとき\(\,2x\,\mathrm{(cm)}\,\)になっているので
周囲\(\,y\,\)はその2倍で
　\(\begin{eqnarray}
y&=&2(15+2x)\\
&=&30+4x\\
&=&\underline{　4x+30　}
\end{eqnarray}\)

これは本当なら問題の条件を与えられたとき先に出している関数です。

与えられた条件でどこまでいえるか自分で出す、それが数学の力です。
得点力とはちょっと違いますけど、少しずつで良いのでこの力をつけていくと良いです。
問1のような小問集合はその計算部分だけになっているだけです。

ただし、試験時間は限られるので今は誘導をうまく使えばそれでいいです。
高校に入って時間ができたら少し考える時間を使って、問題の条件でいえることはどこまでか、これをしないと答えが出ない問題が多くなりますからね。
もちろん、高校入試の応用問題でも同じですが、高校入試の場合はほんの少しの作業で答えは出ますので難しくはありません。

時間が許せば、与えられた条件でどこまでいえるか自分で出す。
やってみてください。

ここでは\(\,y=4x+30\,\)までで十分です。

これが先に出ていた人は自信を持って良いですよ。
数学の力が着いてきているということです。

この『問題の条件でどこまでわかるか』、ある程度出しておくと、
　「あれ？この問題終わってた。」
というのが高校入試です。

(3)これはおまけの計算でしょう。
　\(y=4x+30\)　において\(\,y=102\,\)のときの\(\,x\,\)を求めなさい。
ということです。

　\(\begin{eqnarray}
102&=&4x+30\\
4x+30&=&102\\
4x&=&102-30\\
4x&=&72\\
x&=&\underline{　18　}
\end{eqnarray}\)

次の問4は図形問題です。

⇒　2018年大阪府公立高校入試数学A問題問4の図形問題の解説

平面図形なのでそれほど作業はありません。

⇒　大阪府公立高校入試数学の過去問と解答解説

解説が会員向けでわかりにくい点があるかもしれませんがご容赦下さい。