愛知県公立高校入試2018年A問題問2の確率や文章題の解説

2018年に愛知県で行われた公立高校入試A問題の問2の解説です。
問2の確率や文章題の小問集合の解説になりますが、やり方によっては時間も得点も差が出る問題になっています。
うまく処理すれば後の問題への時間を残せますので、差をつける側になりましょう。

⇒　愛知県2018A日程数学問題　

さいころ2つの出目の積の問題

(1)2つのさいころを投げます。
これは同時に投げても、一つずつ投げても同じだということは説明しなくて良いですね。

　大きいさいころの出た目の数を\(\,\color{red}{a}\,\)
　小さいさいころの出た目の数を\(\,\color{blue}{b}\,\)

とするとき

　\(\,x^2=\color{red}{a}\,\color{blue}{b}\,\)　の解がともに整数

となる確率を求めます。

わかりにくいですけどよく見てください。
左辺は \(\,\color{red}{x^2}\,\) つまり平方数です。
この平方根\(\,x\,\)が整数になるということは\(\,ab\,\)が平方数にならなければなりません。

例えば
　\(\,a=1\,,\,b=2\,\)のときだと\(\,ab=2\,\)
なので
　\(\begin{eqnarray}
x^2&=&2\\
x&=&\pm \sqrt{2}
\end{eqnarray}\)
となり \(x\) は整数では出てきません。
　
　\(\,a=1\,,\,b=4\,\)のときだと\(\,ab=4\,\)
なので
　\(\begin{eqnarray}
x^2&=&4\\
x&=&\pm 2
\end{eqnarray}\)
となり \(x\) は整数になります。

この問題を簡単に言えば、
　「出目の積が平方数になる確率を求めなさい。」
と同じです。

これを考えて問題に取り組んでも良いのですが、
さいころ２つを投げると３６通りの出方があります。

この３６通りを調べた方がはやいです。
普通は樹形図ですがさいころふたつのときは表が便利ですよ。

\(b\)\(\setminus\)\(a\)	1	2	3	4	5	6
1	1	2	3	4	5	6
2	2	4	6	8	10	12
3	3	6	9	12	15	18
4	4	8	12	16	20	24
5	5	10	15	20	25	30
6	6	12	18	24	30	36

３６通りの組み合わせの中で積が平方数になるのは赤字で記した８つです。

この表を使って\(x^2=ab\)を満たす\(\,x\,\)が整数になる組をいくつか探すことで、
逆に平方数のことに気がつく、という方が多いのではないでしょうか。

その方がはやいですよ。
表を書くのに考えることはありませんし、時間は大してかかりません。

調べれば赤字の組だけとわかるので求める確率は
　\(\displaystyle \frac{8}{36}=\underline{　\frac{2}{9}　}\)

とほとんど考えなくても答えが出ます。

文字式の利用法

(2)連続する自然数です。

『覚え太郎』会員はすぐに5つの自然数が書けますが、
問題に指示があるので表現方法が違っていないか確認してください。

文章中の
　\(\,\mathrm{A}\,\)には式
　\(\,a\,,\,b\,,\,c\,,\,d\,\)には自然数
を入れる指示があるので逆にめんどうな問題に思えますが、普通に進めれば簡単に入るように問題ができています。

問題の条件に従って数学の言葉に変換します。
問題に書いてあるのは
　\(\color{magenta}{\fbox{連続する5つの自然数}}\)
　\(\color{magenta}{\fbox{最も小さい数を\(\,n\,\)}}\)
　\(\color{magenta}{\fbox{連続する5つの自然数の和}}\)　
です。

最も小さい数を\(\,n\,\)とすると、
連続する5つの数は（自然数は1ずつ増えるので）
　\(\,n\,,\,n+1\,,\,n+2\,,\,n+3\,,\,n+4\,\)

5つの自然数の和は

　\(\hspace{10pt}n+(n+1)+(n+2)+(n+3)+(n+4)\\
=5n+10\\
=5(n+2)\)

と言われたとおり計算すると答えが出ています。

最も小さい数を\(\,n\,\)とすると、
最も大きい数は\(\,\color{red}{n+4}\,\)と表され、
連続する自然数の和は\(\,\color{red}{5}(n+\color{red}{2})\,\)と表され、
小さい方から\(\,\color{red}{3}\,\)番目の\(\,n+2\,\)の\(\,\color{red}{5}\,\)倍になっています。

　\(\,\mathrm{A}：n+4\,\)　\(\,a：5\,\)　\(\,b：2\,\)　\(\,c：3\,\)　\(\,d：5\,\)

ここは数学の基本だと知っている『覚え太郎』会員には物足りないでしょうが、
さらっと終わらせて次に進みましょう。ｗ

比例定数の範囲

(3)問題を見ると、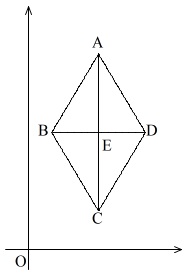
　ひし形？図形の問題か？
と思えますが、
　\(y=ax^2\)
の比例定数（\(\,\color{red}{a}\,\)）の範囲を求める関数問題です。

　\(y=ax^2\) がひし形と交わる点または部分がある

ときの\(\,a\,\)の範囲を求めます。

図で簡単にですが部分的に見てみると

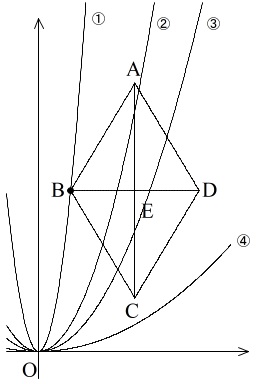
①②③は交わっているけど、④は交わっていない。

問題になりそうなところは点\(\,\mathrm{C}\,\)と点\(\,\mathrm{D}\,\)あたりです。
左側は\(\,\mathrm{B}\,\)を通るときの①が境界になるのはわかりますからね。

図形でも関数でもやることは同じなのですが、
ここでは座標を書き込んでいきましょう。
見えてくることがたくさん増えてくるからですよ。

与えられている条件は、

　四角形\(\,\mathrm{ABCD}\,\)はひし形
　\(\,\mathrm{AC=2BD}\,\)　
　点\(\,\mathrm{A}\,(\,\color{red}{3\,,\,10}\,)\,\)
　点\(\,\mathrm{E}\,(\,\color{red}{3\,,\,6}\,)\,\)

これからわかることは

　点\(\,\mathrm{A,E,C}\,\)の\(\,x\,\)座標は同じ\(\,x=3\,\)。
　\(\,\mathrm{AE=4}\,\)だから\(\,\mathrm{EC=AE=4}\,\)なので\(\,y\,\)座標が\(\,4\,\)下がって
　\(\,\mathrm{C}\,(\,\color{red}{3\,,\,2}\,)\,\)

　\(\,\mathrm{AC=2BD}\,\)から\(\,\mathrm{BD=4}\,\)
ひし形だから
　\(\,\mathrm{BE=ED=2}\,\)
このことと\(\,\mathrm{B,E,D}\,\)の\(\,y\,\)座標が同じ\(\,y=6\,\)なので
　\(\,\mathrm{B}\,(\,\color{red}{1\,,\,6}\,)\,\)　\(\,\mathrm{D}\,(\,\color{red}{5\,,\,6}\,)\,\)

長々と書いていますが座標上で書き込めば簡単です。
ただし、この作業を自分でするかどうかは大きな差になります。

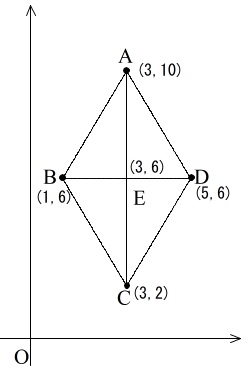
\(\,y=ax^2\,\)は\(\,\mathrm{C}\,\)を通るときが一番外に広がるのか、\(\,\mathrm{D}\,\)を通るとき一番開くのか、それを\(\,\mathrm{C,D}\,\)を代入して確認します。

左の端、つまり\(\,y=ax^2\,\)が一番とがるときは点\(\,\mathrm{B}\,\)を通るときだというのはわかるので、
点\(\,\mathrm{C,D}\,\)ときを調べるのです。
もしかしたら同じ比例定数のとき両方の点を通るかもしれない。

こういう微妙なときは具体的に調べていくのが一番です。

　\(\,y=ax^2\,\)が\(\,\mathrm{C}\,(\,3\,,\,2\,)\,\)を通るとき
　\(2=a\times (3)^2\)　から　\(\displaystyle a=\frac{2}{9}\)

　\(\,y=ax^2\,\)が\(\,\mathrm{D}\,(\,5\,,\,6\,)\,\)を通るとき
　\(6=a\times (5)^2\)　から　\(\displaystyle a=\frac{6}{25}\)

また
　\(\,y=ax^2\,\)が\(\,\mathrm{B}\,(\,1\,,\,6\,)\,\)を通るとき
　\(6=a\times (1)^2\)　から　\(a=6\)

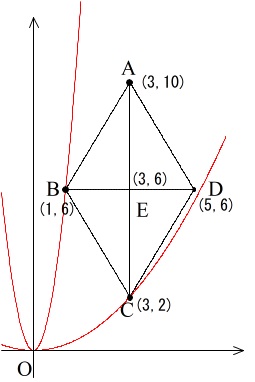
よって比例定数\(\,a\,\)の範囲は
　
　\(\displaystyle \underline{　\frac{2}{9}≦a≦6　}\)

\(\displaystyle \frac{2}{9}\,\)と\(\displaystyle \,\frac{6}{25}\,\)の大小比較は、
小数にしてもいいし、分母をそろえて分子の大きさで比べても良いです。

ある程度の大小さえわかれば良いので、ここでは小数にした方がはやいかな？
　\(\displaystyle \,\frac{2}{9}=0.22\cdots\,\)

　\(\displaystyle \,\frac{6}{25}=0.24\,\)

分数だと分母をそろえて分子の大きさを比較します。
（分母の計算はする必要はありません。）

　\(\displaystyle \frac{2}{9}=\frac{2\times 25}{9\times 25}=\frac{50}{9\times 25}\)

　\(\displaystyle \frac{6}{25}=\frac{6\times 9}{25\times 9}=\frac{54}{25\times 9}\)

だから小さい \(\displaystyle \frac{2}{9}\) が最小になります。

2点間の距離と1次関数

(4)円形の遊歩道を兄弟が逆向きに歩く問題です。

この問題は意味を理解するまでに時間がかかったかもしれませんね。
①②に共通することは
　\(\color{red}{\fbox{逆向きに一定の速さで歩き、１周する}}\)
ということです。

後まで読んでみると兄弟は同じ速さで歩いています。
　
①兄弟は逆向きに同時に出発して二人とも２４分で１周します。
そのときの兄弟間の短い弧の長さを表したグラフがあります。

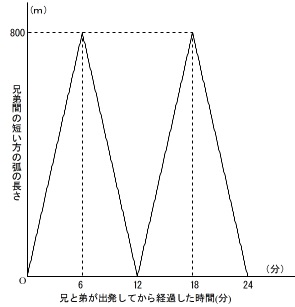
このグラフが意味していることをちょっと説明しておきます。
最初は同じ位置から出発するので、短い弧は\(\,0\,\)から始まって増加しています。

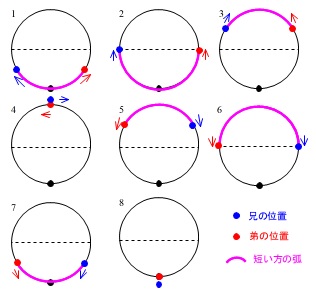
　・最初の直線の上昇は図の\(\,1\,\)の場面で弧の長さは段々長くなります。
　・頂点になっている最大値のところは\(\,2\,\)の場面でちょうど反対側にいるときです。
　・次の減少している直線部分は\(\,3\,\)の場面で、二人とも進むと短い弧は上側で段々短くなります。
　・二人が出会ったときが\(\,4\,\)の場面で、弧の長さは\(\,0\,\)です。
　・また増加し始めている直線は出会ってからさらに反対側に進んでいる場面\(\,5\,\)です。
　・再度最大になっているところは1回目と反対側に兄弟がいる場面\(\,6\,\)です。
　・また減少し始めているのは出発地点に二人とも近づいている場面\(\,7\,\)です。
　・最後の弧の長さが0のところは二人とも1周してきた終点\(\,8\,\)の場面です。
※
私は何に時間をかけて説明しているのでしょう？
『覚え太郎』会員はこれくらい書き出してわかっているだろうに。笑

この弧の長さの最大を表しているのは、ちょうど反対側にいるときの弧の長さです。

このことから\(\,1\,\)周の長さは
　\(800\times 2=\underline{　1600\,\mathrm{(\,m\,)}　}\)
だとわかります。

ここで時間をかけている場合ではありません。
ここは円上の点を動かしてすぐに求めておきましょう。ｗ

②今度は弟が先に出発し、兄が遅れて出発します。

進み方は①の場合と同じで逆方向です。
速さも弟と同じ速さです。

つまり、出発地点が違うだけで動き方は①と同じです。

弟は先に\(\,6\,\)分間歩いています。

二人で歩いて\(\,6\,\)分間で\(\,800\,\mathrm{m}\,\)の弧を描いたので、一人だと\(\,400\,\mathrm{m}\,\)です。

\(\,6\,\)分後に兄が出発してからの時間を\(\,x\,\)とするので、
\(\,x=0\,\)のときの兄弟間の弧の長さ\(\,y\,\)は\(\,y=400\,\)です。

そのとき弟はどこにいるかというと、
\(\,\mathrm{A}\,\)から\(\,90°\,\)の位置です。
そこから同じ速さで逆向きに進むので、\(\,45°\,\)ずつ進んだときに反対になります。
そのときの時間は兄が出発してから\(\,3\,\)分後です。

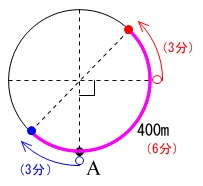
だから　\(\,x=3\,\)　のとき　\(\,y=800\,\)

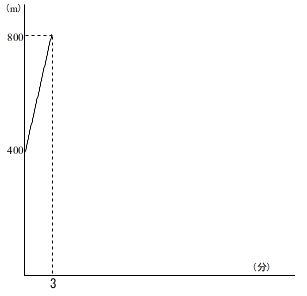
さらに二人ともが歩くので、弧の長さは短くなりますが、出会うまでは減り続けます。
出会うのはそれから\(\,6\,\)分後、兄が出発してからは\(\,9\,\)分後で、

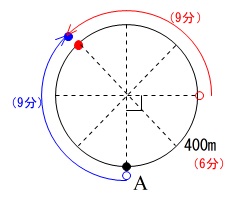
　\(\,x=9\,\)のとき\(\,y=0\,\)となります。
兄が出発した3分後から9分後までのグラフは、
\(\,x=3\,\)から\(\,x=9\,\)までの変化になります。
　\(\,(\,3\,,\,800\,)　(\,9\,,\,0\,)\,\)　を通る直線です。

この後は24分後弟が\(\,\mathrm{A}\,\)に戻るまでは①と同じ変化を繰り返します。
ただし、弟が\(\,\mathrm{A}\,\)に戻ったときに兄はまだ\(\,\mathrm{A}\,\)には戻っていません。
兄が出発したときに弟がいた地点にいます。

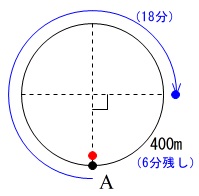
このとき兄が出発してから\(\,18\,\)分後で、残りの長さは\(\,400\,\mathrm{m}\,\)です。
座標で表すと　\(\,(\,18\,,\,400\,)\,\)　です。
ここからは兄だけが歩いて\(\,\mathrm{A}\,\)に向かいます。
（弟は\(\,\mathrm{A}\,\)で兄を待っています。）
弧の減り方も半分になりますが、\(\,24\,\)分で\(\,1\,\)周するというのは変わらないので、
\(\,24\,\)分後残りの弧の長さは\(\,0\,\)です。
　\((\,24\,,\,0\,)\)

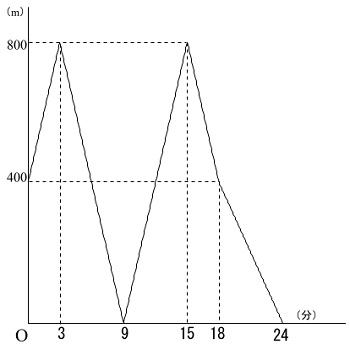
これが答えとなるグラフです。

解答用紙には目盛りが付いているので合わせるように直線をつなげば良いですよ。

この問題では必要ないですけど関数として1次関数をそれぞれ表しておくと、

\(\,0\,≦\,x\,≦\,3\,\)
　\(\displaystyle y=\frac{800}{6}x+400\)

\(\,3\,≦\,x\,≦\,9\,\)
　\(\displaystyle y=-\frac{800}{6}x+1200\)

\(\,9\,≦\,x\,≦\,15\,\)
　\(\displaystyle y=\frac{800}{6}x-1200\)

\(\,15\,≦\,x\,≦\,18\,\)
　\(\displaystyle y=-\frac{800}{6}x+2800\)

\(\,18\,≦\,x\,≦\,24\,\)
　\(\displaystyle y=-\frac{\color{red}{400}}{6}x+1600\)

傾きは時間と弧の長さとの変化を分かり易くするために約分していません。

この問題の考え方は他にもあります。

例えば、
数直線上で原点に兄と弟がいて、\(\,\pm 400\,\)　までを折り返し地点として、
二人が逆向きに速さ\(\displaystyle \frac{1600}{24}=\frac{200}{3}\)で動いて、
その間の距離を\(\,y\,\)とすれば同じ問題になります。

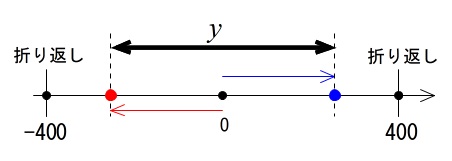
この考え方をすれば最大値が\(\,800\,\)を超えることがないというのはすぐにわかります。
この場合は短いとか、長いとかは考えなくて良くて楽ですので自分でやってみてください。
②の場合は出発地点の置き方が変わります。