2018年愛知県公立高校入試Ａ日程の数学問3図形問題の解説

2018年(平成30年)度に愛知県で行われた公立高校入試Ａ日程の数学問3の解説です。
問3は図形総合問題で、角度、線分、面積比、体積を求めることになります。
空間図形は平面図形より少し手順は多くなりますが覚えておくこと、考え方は同じす。

大問3は図形問題が(1)～(3)まで3つありますが、3つの問はつながりがありません。

問題を見た瞬間では気がつかないですけど、こういうときは落ち着いて取り組んで下さい。
時間かかりそうに見えるけど一つひとつは基本の組み合わせです。

問題は愛知県の公式サイトにもあります。

⇒　2018年度愛知県A日程数学問題　

平面における角度

(1)円周上の点があって、角度がある。
円周角の定理を利用するんだろうな、と推測しても良いくらいです。
ただ、思い込みはよくありません。

条件を図示することから始めましょう。
問題にある条件は
　\(\,\mathrm{A,B,C,D}\,\)は円周上の点
　\(\,\mathrm{AB=AD}\,\)
　\(\,\mathrm{EB=EC}\,\)
　\(\,\mathrm{∠BEC}=106°\,\)
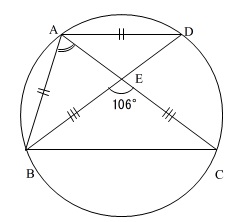これですべての角度がわかります。

円周角や二等辺三角形の底角で等しい角など、
数値以外のわかることをある程度書き込みます。
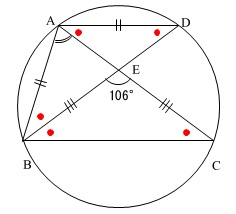数値を出します。
　　\(\,\mathrm{EB=EC}\,\)
から引き出しましょう。
（角度記号　°　を省略して計算しますが答えにはつけましょう。）
\(\,\mathrm{△EBC}\,\)は二等辺三角形なので底角2つは等しく
　\(\begin{eqnarray}
\mathrm{∠EBC}&=&\mathrm{∠ECB}\\
&=&\frac{180-106}{2}\\
&=&\frac{74}{2}\\
&=&37
\end{eqnarray}\)
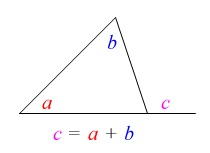を使うと
　\(\,\mathrm{∠BAE+∠ABE=∠BEC}\,\)
なので
　\(\,\mathrm{∠BAE}=106-37=\underline{69}\,\)

　（答え）　\(\,\underline{　69　}\,\)度

角度を求めるときはわかった角度を書き込んでいけば必ず到達できます。
なかなか到達しない場合、何か使っていない条件があるはずです。

もう一度、最初から条件の確認をしてみると良いですよ。

まだまだあるので先に進みます。

平面図形の線分の長さと面積比

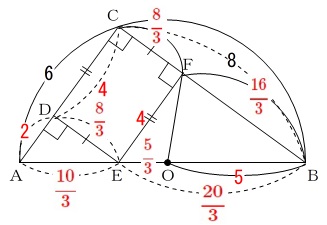
(2)半円の中の三角形の\(\,1\,\)辺が直径です。
これも条件を図示します。
相似な三角形が多くてどれを使うか迷うくらいです。
書き込めることを書き出してみますので確認して下さい。

　\(\,\mathrm{AB}\,\)が直径なので\(\,\mathrm{∠ACB}=90°\,\)
　四角形\(\,\mathrm{CDEF}\,\)は長方形
　\(\,\mathrm{CA=6　,　CB=8}\,\)
　\(\,\mathrm{ＣＤ：ＤＥ}=3：2\,\)

相似を抜き出すと
　\(\,△\mathrm{ACB}\,\)　∽　\(\,△\mathrm{ADE}\,\)　∽　\(\,△\mathrm{EFB}\,\)

①「線分\(\,\mathrm{FE}\,\)の長さを求めよ。」なので、
\(\,\mathrm{FE}\,\)を含んだ三角形を選んだ方が良いかもしれません。
どれを選んでも出てくるとは思いますができるだけ直接求めたいでしょう？

　\(\,△\mathrm{ACB}\,\)　∽　\(\,△\mathrm{EFB}\,\)

を使いましょう。

ここでちょっとしたことで計算を楽にする方法をとります。
普通は求めたいものを文字で置くのですが、
　\(\,\mathrm{ＣＤ：ＤＥ}=3：2\,\)
なので、
　\(\,\mathrm{ＣＤ：ＤＥ}=3x：2x\,\)
とおきます。
すると、四角形\(\,\mathrm{CDEF}\,\)は長方形なので
　\(\,\mathrm{DC=FE}=3x\,\)
　\(\,\mathrm{DE=CF}=2x\,\)
とおけて残りの線分の長さは
　\(\,\mathrm{BF}=8-2x\,\)
また直角三角形\(\,\mathrm{ACB}\,\)の斜辺は三平方の定理から
　\(\begin{eqnarray}
\mathrm{AB}^2&=&\mathrm{AC^2+CB^2}\\
&=&6^2+8^2\\
&=&36+64=100
\end{eqnarray}\)
\(\,\mathrm{AC}＞0\,\)から　\(\,\mathrm{AB}=10\,\)
※
この直角三角形の比\(\,3：4：5\,\)を覚えておいても良いです。
すべての直角三角形ではないので注意しておいて下さい。

これでニコちゃんマークを作ります。
（ニコちゃんマークって何？と感じる人は無視して下さい。）
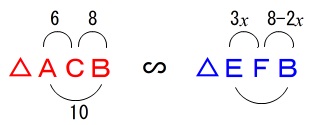相似を見つけたら高校生になってもこれを書くといいですよ。
方べきの定理とかわかりにくい定理を覚えなくても良くなります。

ここで注意して欲しいのは求めるものは\(\,\color{red}{x}\,\)ではなく、\(\,3x\,\)だということです。
分数を使いたくないので文字式の使い方を変えていることは忘れないようにしましょう。　

図は見なくて良いので相似比を利用して比例式を立てます。
　\(\begin{eqnarray}
\mathrm{AC:EF}&=&\mathrm{CB:FB}\\
6:3x&=&8:(8-2x)\\
\end{eqnarray}\)

この比例式は
　\(\begin{eqnarray}
\mathrm{AC:CB}&=&\mathrm{EF:FB}\\
6:8&=&3x:(8-2x)\\
\end{eqnarray}\)

でも同じですよ。解きます。

　　\(\begin{eqnarray}
6:3x&=&8:(8-2x)\\
3x\times 8&=&6\times (8-2x)\\
24x&=&48-12x\\
24x+12x&=&48\\
36x&=&48\\
\displaystyle x&=&\frac{48}{36}=\frac{4}{3}
\end{eqnarray}\)

よって
　\(\begin{eqnarray}
\displaystyle \mathrm{FE}&=&3x\\
&=&3\times\frac{4}{3}=\underline{　4　}
\end{eqnarray}\)

これですべての長さが書き込めます。
　\(\begin{eqnarray}
\displaystyle \mathrm{CF}&=&2x\\
\displaystyle &=&2\times \frac{4}{3}\\
\displaystyle &=&\color{red}{\frac{8}{3}}\\
\end{eqnarray}\)

　\(\begin{eqnarray}
\displaystyle \mathrm{BF}&=&8-2x\\
\displaystyle &=&8-\color{red}{\frac{8}{3}}\\
\displaystyle &=&\frac{8\times 3-8}{3}\\
\displaystyle &=&\color{red}{\frac{16}{3}}
\end{eqnarray}\)

などを計算して書き込めば、
人の計算見て、自分でやったみたいになる人いるのでここは省略します。
すべての長さが必要になる訳ではありませんので、問題に合わせて計算すれば良いですが、
出しておけばどんな問題でも答えは出ます。

②\(\,\mathrm{△FEO}\,\)の面積は\(\,\mathrm{F}\,\)から\(\,\mathrm{AB}\,\)への垂線を出せば具体的に求まります。
それは別の問題でもよく出てくるのでここでは相似比と面積の圧縮で解きましょう。

　\(\,△\mathrm{ABC}\,\)　∽　\(\,△\mathrm{EBF}\,\)

相似比は　\(\,6:4=3:2\,\)　です。
面積比は　\(\,3^2:2^2=9:4\,\)　です。

このことから
　\(\displaystyle △\mathrm{\color{red}{EBF}}=\color{blue}{\frac{4}{9}\times △\mathrm{ABC}}\,\)

\(\,△\mathrm{EBF}\,\)と\(\,△\mathrm{FEO}\,\)は高さが同じになりますので面積比は底辺の比です。

底辺の比は
　\(\displaystyle \,\mathrm{EB:EO}=\frac{20}{3}:\frac{5}{3}=4:1\,\)
なので
　\(\displaystyle \,△\mathrm{FEO}=\frac{1}{4}\times △\mathrm{\color{red}{EBF}}\,\)

よって
　\(\begin{eqnarray}
\displaystyle △\mathrm{FEO}&=&\frac{1}{4}\times△\mathrm{\color{red}{EBF}}\\
\displaystyle &=&\frac{1}{4}\times\color{blue}{\frac{4}{9}\times △\mathrm{ABC}}\\
\displaystyle &=&\frac{1}{9}\times △\mathrm{ABC}
\end{eqnarray}\)

　（答え）\(\,\displaystyle \underline{　\frac{1}{9}　}\,\)倍

説明長いけどやっていることは単純で、短時間で終わります。
自分でやってみるとわかりますよ。

立体図形の線分の求め方と回転体の体積

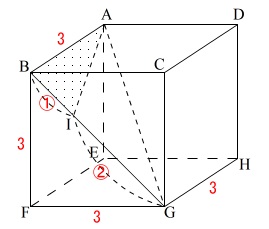
(3)立方体なので少しは楽になります。
後半の回転体は円すいですよ。中学1年でやったことです。

まずは条件を詳しくでなくていいので簡単に書き込みます。
立体、空間は立体のまま考えない、というのが原則です。
（私が勝手に言っていることなので気にしなくて良いですよ。）
わかることはたくさんありますが、問題の中で処理します。

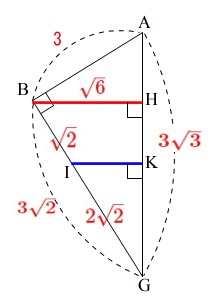
①線分\(\,\mathrm{AI}\,\)の長さを求めます。

空間図形では平面を抜き出して考えると良いのですよね？
レポートをよく読んでる人には耳にたこができるほど見かけているはずです。

\(\,\mathrm{AI}\,\)を含む面を抜き出します。
線分\(\,\mathrm{AB}\,\)は面\(\,\mathrm{BFGC}\,\)に垂直なので
　\(\,\mathrm{∠ABG}=90°\,\)
これが読み取れるくらいは練習しておかないと満点は難しいですね。
中学1年の内容です。
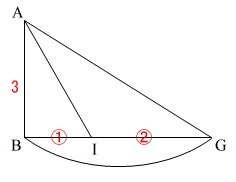線分\(\,\mathrm{BG}\,\)の長さが欲しいです。
三平方の定理から
　\(\begin{eqnarray}
\mathrm{BG}^2&=&\mathrm{BF^2+FG^2}\\
&=&3^2+3^2\\
&=&9+9=18
\end{eqnarray}\)

\(\,\mathrm{BG}＞0\,\)だから
　\(\begin{eqnarray}
\mathrm{BG}&=&\sqrt{18}\\
&=&\color{red}{3\sqrt{2}}
\end{eqnarray}\)

　\(\,\mathrm{BI:IG}=1:2\,\)
なので
　\(\,\mathrm{BI}=\color{red}{\sqrt{2}}\,\)
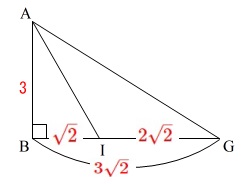\(\,\mathrm{△ABI}\,\)に三平方の定理を使うと
　\(\begin{eqnarray}
\mathrm{AI^2}&=&\mathrm{AB^2+BI^2}\\
&=&3^2+(\sqrt{2})^2\\
&=&9+2=11
\end{eqnarray}\)

\(\,\mathrm{AI＞0}\,\)だから
　\(\,\mathrm{AI=\underline{\sqrt{11}}}\,(\mathrm{cm})\)

順を追って長さを出せばすぐに答えが出てくる簡単な問題です。
平面を抜き出さない人にとってはいつまでたっても難しいと感じる立体問題ですけどね。

②回転体の問題を解くコツは、回転体ができたとするときの正面図です。
縦でも横でも良いのですが真正面から見た断面図が欲しいのです。

この問題では回転する前の図があります。
これを回転軸を水平か垂直にして見やすくします。
※高校生で積分好きな人は横の方が慣れてて使いやすいですね。

ところでこの問題はよく見る問題ですが、できない人多すぎです。
中学1年の内容から復習することをおすすめします。

\(\,△\mathrm{ABI}\,\)を回転させてできる体積は簡単に出す方法はあります。
しかし、普通は回転体から回転体を引きます。
※
『超え太郎』マスターは知っているので簡単に答えを出しても良いですが検算はしておきましょう。

\(\,△\mathrm{ABG}\,\)を\(\,\mathrm{AG}\,\)を軸として回転させた円すいから、
\(\,△\mathrm{AIG}\,\)を\(\,\mathrm{AG}\,\)を軸として回転させた円すいを引けば良いだけです。

必要になってくるのは回転半径です。
　\(\,\mathrm{B}\,\)から\(\,\mathrm{AG}\,\)に下ろした垂線の足を\(\,\mathrm{H}\,\)
　\(\,\mathrm{I}\,\)から\(\,\mathrm{AG}\,\)に下ろした垂線の足を\(\,\mathrm{K}\,\)
としましょう。
（この問題は答えだけなので記号はなくても計算を進めて良いです。）
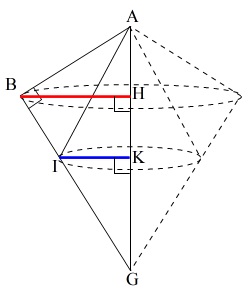答えになる回転体の体積はどうでも良いです。
そんなものは試験の時に、間違えたら何にもならないので、見直しで確実性を増すしかありません。
しかし、どの問題でも確実にできることを大切にしておきましょう。

何をするのでしたか？

平面を抜き出すんでしょ？
何度言ってもやらないって、わざと時間をかけて、間違えたいのですか？

みんながみんなそうではない、と思いたいので繰り返します。
求めたい辺を含む面を抜き出して考えます。
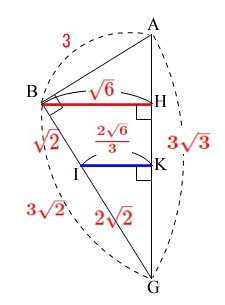
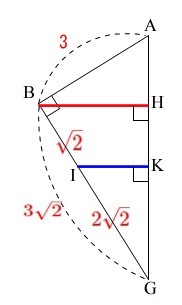\(\,\mathrm{AG}\,\)の長さを出しておきます。
\(\,\mathrm{△ABG}\,\)が直角三角形なので
　\(\begin{eqnarray}
\mathrm{AG^2}&=&\mathrm{AB^2+BG^2}\\
&=&3^2+(3\sqrt{2})^2\\
&=&9+18\\
&=&27
\end{eqnarray}\)

\(\,\mathrm{AG}＞0\,\)だから
　\(\,\mathrm{AG}=\color{red}{3\sqrt{3}}\,\)

相似な三角形がたくさんあるので相似を使って\(\,\mathrm{BH}\,\)を求めてみて下さい。
ここでは違う見方をしておきます。

1つの\(\,\color{red}{\mathrm{△ABC}}\,\)の面積は変化しません。

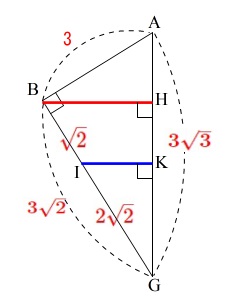
　底辺を\(\,\mathrm{BG}\,\)、高さを\(\,\mathrm{AB}\,\)と見る面積
　\(\begin{eqnarray}
\displaystyle \mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{BG} \times \mathrm{AB}\\
\displaystyle &=&\frac{1}{2}\times 3\sqrt{2}\times 3\\
\displaystyle &=&\frac{9\sqrt{2}}{2}
\end{eqnarray}\)
と
底辺を\(\,\mathrm{AG}\,\)、高さを\(\,\mathrm{BH}\,\)と見る面積
　\(\begin{eqnarray}
\displaystyle \mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AG} \times \mathrm{BH}\\
\displaystyle &=&\frac{1}{2}\times 3\sqrt{3}\times \mathrm{BH}\\
\displaystyle &=&\frac{3\sqrt{3}\times \mathrm{BH}}{2}
\end{eqnarray}\)

は同じでないとおかしい。

　\(\begin{eqnarray}
\displaystyle \frac{3\sqrt{3}\times \mathrm{BH}}{2}&=&\frac{9\sqrt{2}}{2}\\
3\sqrt{3}\times \mathrm{BH}&=&9\sqrt{2}\\
\displaystyle \mathrm{BH}&=&\frac{9\sqrt{2}}{3\sqrt{3}}\\
\displaystyle &=&\frac{3\sqrt{2}}{\sqrt{3}}\\
\displaystyle &=&\frac{3\sqrt{2}\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\\
\displaystyle &=&\frac{3\sqrt{6}}{3}\\
&=&\color{red}{\sqrt{6}}
\end{eqnarray}\)
\(\,\mathrm{△GBH}\,\)　と　\(\,\mathrm{△GIK}\,\)
は相似で、
　相似比は　\(\,3:2\,\)
だから
　\(\begin{eqnarray}
\mathrm{BH:IK}&=&3:2\\
\sqrt{6}:\mathrm{IK}&=&3:2\\
3\times \mathrm{IK}&=&2\times \sqrt{6}\\
\displaystyle \mathrm{IK}&=&\color{red}{\frac{2\sqrt{6}}{3}}
\end{eqnarray}\)

ここまでは平面を抜き出して、相似を使って計算するだけです。

円すいの体積ですが、
2つに分ける必要はありません。

例えば\(\,\mathrm{△ABG}\,\)を回転させた円すいを

　底面を\(\,\mathrm{BH}\,\)を半径とする円
　高さを\(\,\mathrm{AH}\,\)
と
　底面を\(\,\mathrm{BH}\,\)を半径とする円
　高さを\(\,\mathrm{HG}\,\)

の2つが合わさった形をしていますが、
　底面を\(\,\mathrm{BH}\,\)を半径とする円
　高さを\(\,\mathrm{\color{red}{AG}}\,\)
とする1つの円すいと計算しても同じです。

やったことがない人はいないとは思いますが説明しておきます。
底面の円の半径が\(\,r\,\)で、
高さが\(\,a\,\)と\(\,b\,\)の円すいが上下にあるとき、

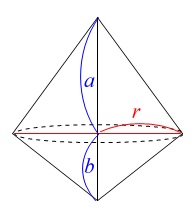
　\(\displaystyle \hspace{10pt}\frac{1}{3}\pi \,r^2\times \color{blue}{a}+\frac{1}{3}\pi ,r^2 \times \color{blue}{b}\\
\displaystyle =\frac{1}{3}\pi \,r^2\times (\color{blue}{a+b})\)

のように1つの円すいとして計算できます。

これを利用しながら答えを出しましょう。

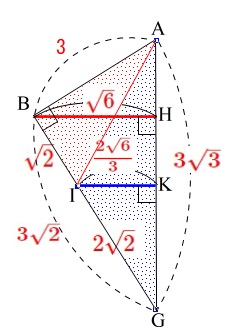
　\(\,\mathrm{△ABG}\,\)の回転体の体積
から
　\(\,\mathrm{△AIG}\,\)の回転体の体積
を引くと
　\(\,\mathrm{△ABI}\,\)の回転体の体積
になります。

三角形\(\,\mathrm{ABC}\,\)の回転体の体積を\(\color{black}{\fbox{　△ABC　}}\)などと表すことにすると

　\(\begin{eqnarray}
\displaystyle \mathrm{\color{black}{\fbox{　△ABG　}}}&=&\frac{1}{3}\pi \times\mathrm{BH}^2\times \mathrm{AG}\\
&=&\frac{1}{3}\pi \times(\sqrt{6})^2\times 3\sqrt{3}\\
&=&\frac{1}{3}\pi \times 6 \times 3\sqrt{3}\\
&=&6\sqrt{3}\pi
\end{eqnarray}\)

　\(\begin{eqnarray}
\displaystyle \mathrm{\color{blue}{\color{blue}{\fbox{　△AIG　}}}}&=&\frac{1}{3}\pi \times \mathrm{IK}^2\times \mathrm{AG}\\
&=&\frac{1}{3}\pi \times \left(\frac{2\sqrt{6}}{3}\right)^2\times 3\sqrt{3}\\
&=&\frac{1}{3}\pi \times \frac{24}{9} \times 3\sqrt{3}\\
&=&\color{blue}{\frac{8\sqrt{3}}{3}\pi}
\end{eqnarray}\)

よって\(\,\color{red}{△\mathrm{ABI}}\,\)の回転体の体積は
　　\(\begin{eqnarray}
\displaystyle \mathrm{\color{red}{\color{red}{\fbox{　△ABI　}}}}&=&6\sqrt{3}\pi-\color{blue}{\frac{8\sqrt{3}}{3}\pi}\\
&=&\frac{18\sqrt{3}-8\sqrt{3}}{3}\pi \\
&=&\underline{　\frac{10\sqrt{3}}{3}\pi　}(\mathrm{cm^3})
\end{eqnarray}\)

終わりです。
問題に『（問題はこれで終わりです。）』と書いてくれています。
これはありがたいです。
「自分の問題用紙だけ抜けているのではないか？」
と思うことありますからね。ない？

ここまで読んでくれた人だけが知ることができる過去問対策のポイントです。

なぜ最後の問題をここまで長々と説明したかというと、
これくらいの計算は待っている、という覚悟をして欲しかったからです。

別の方法で、もっと楽に答えを出す方法もあります。
しかし、入試の現場でそれがすぐに出てくる人はこのページを読んではいないでしょう。
だから道筋が見えたら突っ走る方法で説明してあります。

過去問を見るというのはそういうことです。
どのような問題が出ているかではなく、
どれくらいの作業量と計算量が必要かを知ることです。

全国の公立高校入試は問題内容は似ています。
教科書は違っても日本全国同じ内容を中学で勉強するんだから当然です。
しかし、レベルの違いが出てきます。
それが作業量と計算量です。

それをするのが過去問対策ですよ。
それを標準的？な愛知県でも示しておきました。

自分は『覚え太郎』『超え太郎』を見続けてきたといえるなら、

⇒　中学数学のすべてを短期攻略する『覚え太郎』

レポートも何度も読んだといえるなら、
最低限の努力をしてきたと言えるなら、
　最後の問題3(3)②くらい計算する！
という気持ちで全問に当たってみて下さい。
きっと満点に近い点数がとれます。

「え？もう終わり？」
と感じることもあると思いますよ。

⇒　愛知県公立高校入試2018(平成30年度)A日程 数学問題の解説(問1)

全体通してもう一度通しでやって見ると良いです。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

あなたが受験する都道府県でなくても数学の内容は同じです。
過去問では傾向を知り、対策の目安にすれば良いですよ。