2018年度大阪府公立高校入試Ｂ問題の数学問4空間図形の解説

2018年（平成30年）度に行われた大阪府公立高校入試Ｂ問題の数学問4の解説です。
問4は立体図形の問題ですが立体問題としては標準的な問題です。
ポイントは立体で考えない、という空間図形の基本通りです。

問題にある大きな条件はたった2行です。

⇒　大阪府2018Ｂ数学問題　

ねじれの位置の再確認

\(\,問4\,\)は空間図形ですがこの問題を通じて与えられている条件は

　立体\(\,\mathrm{A-BCD}\,\)は三角すい
　底面の\(\,\mathrm{△BCD}\,\)が\(\,1\,\)辺\(\,6\,\)の正三角形
　\(\,\mathrm{AB=AC=AD}=9\,\)
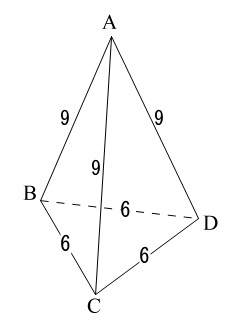全体を通じてこの条件は必要です。

これにそれぞれの問題の条件が加わります。

(1)条件が加わります。
　\(\,\mathrm{AE:ED}=2：3\,\)
　\(\,\mathrm{EF}\,\)∥\(\,\mathrm{DC}\,\)
　\(\,\mathrm{GF}\,\)∥\(\,\mathrm{AB}\,\)
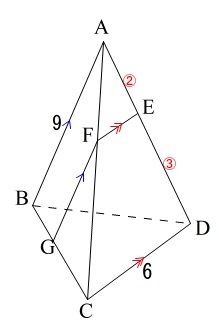①辺\(\,\mathrm{DC}\,\)とねじれの位置にある辺です。

ねじれの位置にあるとは

　交わりもなく平行でもない

ことをいいます。

　（答え）辺\(\,\mathrm{AB}\,\)

ここでは関係ありませんが、
「交わりがない」とは延長しても交わりがないことですよ。
「線分」ではなく「直線」で考えなくてはなりません。

角度を文字で表すときの条件

②\(\,\mathrm{△ACD}\,\)だけを見ればいい問題です。

　\(\mathrm{∠CAD}=a^{\circ}\,\)とするときの\(\,\mathrm{∠ACD}\,\)

これはレポートでも言っているし何度も言うことになりますが、
立体を立体のまま考えることはしない方がいいです。
平面を抜き出して考えるのですよ。
\(\,\mathrm{△ACD}\,\)を抜き出すと
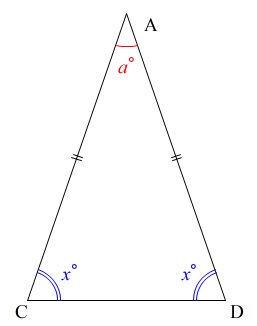角度を文字で表すときは求めるものも文字でおいて、
内角の和で方程式を立てるのがはやいです。
\(\,\mathrm{△ACD}\,\)は二等辺三角形なので

　\(\,\mathrm{∠ACD=∠ADC}=x\,\)

とおくと三角形の内角の和から

　\(\begin{eqnarray}
a+2x&=&180\\
2x&=&180-a\\
x&=&\displaystyle \underline{　\frac{180-a}{2}　}（ 度 ）
\end{eqnarray}\)
または
　\(\displaystyle \underline{　90-\frac{a}{2}　}\)　（度）

問題では「　°」と表していますが、答えでは（度）になって解答用紙に書いてあります。
こういった場合は答えの欄には単位はつけてはダメです。

空間図形で線分の長さを求めるときのポイント

③線分\(\,\mathrm{GC}\,\)の長さです。
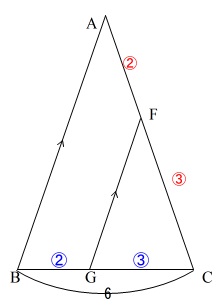\(\,\mathrm{AB}\,\)∥\(\,\mathrm{FG}\,\)なので
　\(\,\mathrm{BG:GC=AF:FC}=2：3\,\)
よって
　\(\begin{eqnarray}
\displaystyle \mathrm{GC}&=&\frac{3}{5}\times \mathrm{BC}\\
&=&\frac{3}{5}\times 6\\
&=&\underline{\frac{18}{5}}
\end{eqnarray}\)

\(\,\mathrm{△ABC}\,\)を抜き出せば、単なる平行線による相似の問題です。

空間図形の線分

(2)の条件は\(\,\mathrm{CH⊥AD}\,\)です。
\(\,\mathrm{H}\,\)は\(\,\mathrm{辺AD}\,\)上の点であれば\(\,\mathrm{BH=CH}\,\)は常に成り立つのですが問題に書いてくれています。
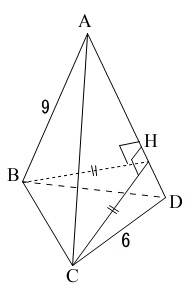\(\,\mathrm{直線AD}\,\)が\(\,\mathrm{平面BCH}\,\)と垂直というのも問題が教えてくれています。
このときは\(\,\mathrm{AD⊥BH}\,\)でもあると言うことですが、
もう一つ、
　\(\,\mathrm{AH}\,\)が三角すい\(\,\mathrm{A-BCH}\,\)の高さだと言うことです。

①線分\(\,\mathrm{CH}\,\)の長さです。
\(\,\mathrm{CH}\,\)を含む面を抜き出しましょう。

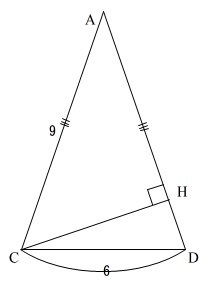
『超え太郎』（三平方の定理）に\(\,\mathrm{AH\,,\,DH}\,\)の長さを一発で出す方法はもありますが普通に三平方の定理を使って求めておきます。

直角三角形は\(\,\mathrm{△AHC}\,\)と\(\,\mathrm{△DHC}\,\)の2つあります。

　\(\mathrm{\color{red}{CH^2}+AH^2=AC^2}\)
　\(\mathrm{\color{blue}{CH^2}+DH^2=DC^2}\)

　\(\,\mathrm{AC=9\,,\,DC=6}\,\)
また
　\(\,\mathrm{AH+HD}=9\,\)
なので
　\(\,\mathrm{HD=9-AH}\,\)
これを上の2つの式に代入すると
　
　\(\begin{eqnarray}
\mathrm{\color{red}{CH^2}+AH^2}&=&\mathrm{AC^2}\\
\mathrm{\color{red}{CH^2}+AH^2}&=&9^2\\
\mathrm{\color{red}{CH^2}}&=&\mathrm{\color{magenta}{9^2-AH^2}}
\end{eqnarray}\)

　\(\begin{eqnarray}
\mathrm{\color{blue}{CH^2}+DH^2}&=&\mathrm{DC^2}\\
\mathrm{\color{blue}{CH^2}+(9-AH)^2}&=&6^2\\
\mathrm{\color{blue}{CH^2}}&=&\color{magenta}{6^2-(9-\mathrm{AH})^2}
\end{eqnarray}\)

文字のままだと見にくいので\(\,\mathrm{AH}=x\,\)としましょう。
最初から\(\,\mathrm{AH}=x\,\)とおいておくと
　\(\mathrm{DH}=9-x\)
となるので方程式は立てやすいですが、
最初からこの方法をとるという人は相当な練習をしている人だろうからあえて不慣れな人向きに流れを見てみました。

関係式を変形していけば文字でおきたくなる、ということです。
ポイントになるのは求めたい\(\,\mathrm{CH}\,\)がすぐには求まらない、ということです。
一度消去するのが\(\,\mathrm{CH}\,\)になっているのでややこしいです。
※
後で違う方法を教えるので今は流れを見ておいてください。

　\(\color{red}{\mathrm{CH^2}}=\color{blue}{\mathrm{CH^2}}\)
なので
　\(\begin{eqnarray}
\mathrm{\color{magenta}{9^2-AH^2}}&=&\color{magenta}{6^2-(9-\mathrm{AH})^2}\\
9^2-x^2&=&6^2-(9-x)^2\\
81-x^2&=&36-(81-18x+x^2)\\
81-x^2&=&36-81+18x-x^2\\
81&=&-45+18x\\
18x-45&=&81　（両辺入れかえた）\\
18x&=&81+45\\
18x&=&126\\
x&=&\frac{126}{18}=7
\end{eqnarray}\)

この方程式の処理はあちこちの小問集合でもお伝えしていますが、
3行目4行目を省略しないことで計算ミスが減ります。

　\(\,\mathrm{AH}=7\,\)なので

　\(\begin{eqnarray}
\mathrm{CH^2}&=&9^2-\mathrm{AH^2}\\
&=&9^2-7^2\\
&=&91-49\\
&=&32\\ \\
\mathrm{CH}&=&\pm \sqrt{32}\\
&=&\pm 4\sqrt{2}
\end{eqnarray}\)

\(\,\mathrm{CH＞0}\,\)なので（長さだから）

　\(\,\mathrm{CH}=\underline{4\sqrt{2}}\,\)

地味な計算ですがこれをやらないと満点は取れないのです。
満点とる必要はありませんがこの程度の計算をめんどうだと感じるようであれば高校で通用しません。
\(\,\mathrm{B}\,\)問題を受けると言うことはそれなりに大学への進学を考えているんでしょう？
試験の時にミスなく答えが出るかどうかは別にして、
これがめんどうなら、高校での数学はかなり苦戦する、と断言しておきます。

高さを求めるもう一つの方法

\(\,\mathrm{CH}\,\)は垂線です。
垂線は高さである、とも言えます。

なのでよく使う手法ですが紹介しておきます。
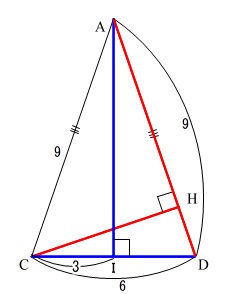\(\,\mathrm{△ACD}\,\)は

　底辺\(\,\mathrm{DC}\,\)、高さ\(\,\mathrm{AI}\,\)の三角形
　底辺\(\,\mathrm{AD}\,\)、高さ\(\,\mathrm{CH}\,\)の三角形

と\(\,2\,\)つの見方ができます。
しかし、面積は\(\,1\,\)つの三角形を見ているので同じです。

だから

　\(\begin{eqnarray}
\displaystyle \frac{1}{2}\times \mathrm{DC\times AI}&=&\frac{1}{2}\times \mathrm{AD\times CH}\\
\mathrm{DC\times AI}&=&\mathrm{AD\times CH}
\end{eqnarray}\)

が成り立ちます。
上の図の直角三角形\(\,\mathrm{ACI}\,\)から三平方の定理によって

　\(\begin{eqnarray}
\mathrm{AI}&=&\sqrt{9^2-3^2}\\
&=&\sqrt{81-9}\\
&=&\sqrt{72}\\
&=&6\sqrt{2}
\end{eqnarray}\)

は容易に出てくるので

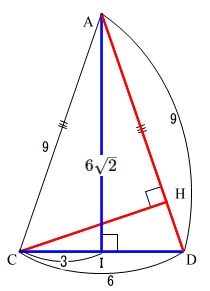
　\(\begin{eqnarray}
\mathrm{DC\times AI}&=&\mathrm{AD\times CH}\\
6\times 6\sqrt{2}&=&9\times \mathrm{CH}\\
9\times \mathrm{CH}&=&6\times 6\sqrt{2}\\
\displaystyle \mathrm{CH}&=&\frac{6\times 6\sqrt{2}}{9}\\
&=&\underline{4\sqrt{2}}
\end{eqnarray}\)

と求めることもできます。
体積にも応用できるので１つ三角形や立体を、
　違った方向から見る
というのもよく使うので覚えておくと良いです。

体積の求め方

体積の求め方はどこまで行っても追っていくのは

　底面積と高さ

です。

ちょっと違うもので球の体積がありますがあれは別物です。
公式は積分を使わないと求められないので覚えて使うしかない、単なる公式利用項目です。
もちろん公式は導けなくても使って良いです。

何故なら、公式だから。笑

違った計算をしているようでも底面積と高さはどこかで使っているので体積を問われたら、
球以外は底面積と高さを探しに行けばほとんど解けます。

立体\(\,\mathrm{A-BCH}\,\)は三角すいです。

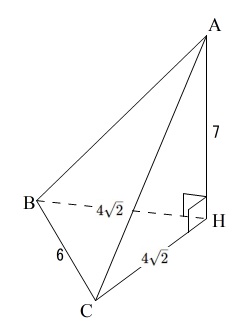
　底面積は\(\,\mathrm{\color{red}{△BCH}}\,\)
　高さは\(\,\mathrm{\color{blue}{AH}}\,\)

すでに必要な長さは出ていますので底面積を求めましょう。

\(\,\mathrm{△BCH}\,\)は二等辺三角形ですが高さとなる辺がありません。
三角形を抜き出して垂線を下ろしましょう。

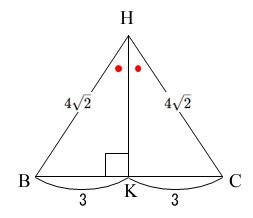
\(\,\mathrm{△BKH}\,\)に三平方の定理を使って

　\(\begin{eqnarray}
\mathrm{HK}&=&\sqrt{(4\sqrt{2})^2-3^2}\\
&=&\sqrt{32-9}\\
&=&\sqrt{23}
\end{eqnarray}\)

よって
　\(\begin{eqnarray}
\displaystyle \mathrm{△BCH}&=&\frac{1}{2}\times \mathrm{BC} \times \mathrm{HK}\\
&=&\frac{1}{2}\times 6 \times \sqrt{23}\\
&=&3\sqrt{23}
\end{eqnarray}\)

高さは\(\,\mathrm{AH}=7\,\)とわかっているので錐体であることに注意して

　\(\hspace{10pt}(立体\mathrm{A-BCH}の体積)\\
\displaystyle =\frac{1}{3}\times 3\sqrt{23}\times 7\\
=\underline{7\sqrt{23}}\)

体積の方が計算が楽に思えるのはそれまでに長さを出しているからですよ。
①が出ていなければ②は出ないかというとそうでもありませんが、誘導されているのでこれが一番楽でしょう。

①がない方が実は体積自体ははやく求めることができるのですが、
長くなったので誘導通りの方法だけにしておきます。

大阪\(\,\mathrm{2018Ｂ}\,\)問題終了です。

⇒　大阪府公立高校入試2018(平成30年度) 数学B問題の解説(問1)

全体でみると説明長いけど、自分でやってみると思ったほどでもないですよ。
というより、これを全国標準の分量として見ておくと良いです。

⇒　大阪府公立高校入試数学の過去問と解答解説

例年それほど変わりないので過去問で分量は知っておくと良いです。