2018年度北海道公立高校入試の数学第2問(裁量問題問1)の解説

2018年(平成30年)度に行われた北海道公立高校入試の数学第2問の解説です。
第2問は裁量問題の問1にもなりますが、因数分解、確率、三角形の面積、基本図形問題の小問集合です。
問題数から考えてもここは短時間で済ませておいた方が良さそうです。

問題は北海道の公式ページでも公表してくれています。

⇒　北海道公立入試2018年数学問題

大問\(\large{\color{black}{\fbox{　2　}}}\)です。
それほど難しい問題があるわけではないのでポイントだけ押さえておきましょう。

因数分解の手順は決まっている

因数分解の手順は、
　1．共通因数の抜き出し
　2．公式利用
これで高校入試の因数分解は終わります。

高校になると手順が増えますので、会員サイトで確認しておいて下さい。

「因数分解しなさい。」
という問題では必ず因数分解できるように問題が作られているので、多少強引に進めても答えは出ます。

例えばこの問題は
　\(x^2-4x-12\)
と\(\,x^2\,\)の係数が\(\,1\,\)なので
　\((x+a)(x+b)\)
という形になります。

次に定数項が\(\,-12\,\)なので
　\((x+1)(x-12)\)
　\((x-1)(x+12)\)
　\((x+2)(x-6)\)
　\((x-2)(x+6)\)
　\((x+3)(x-4)\)
　\((x-3)(x+4)\)
のどれかのはずです。
これを展開して\(\,x\,\)の1次の項が一致すればそれが答えです。

ただ全部展開するのも時間がかかりますので、
定数項の\(\,-12\,\)になる積の組み合わせを抜き出します。
かけて\(\,12\,\)になるのは
　\(\color{black}{\fbox{　1×12　}}\)　\(\color{black}{\fbox{　2×6　}}\)　\(\color{black}{\fbox{　3×4　}}\)
の3組で、かけてマイナスなのでどちらかがマイナスになります。
3組のうち、足して\(\,x\,\)の\(\,1\,\)次の係数\(\,-4\,\)になるのは
　\(\color{magenta}{\fbox{　2　と　－6　}}\)
の組なので
　\(x^2-4x-12=\underline{(x+2)(x-6)}\)

実際の問題用紙の上では
　1　　12
　2　　6
　3　　4
（後は左右が入れ替わるだけなので必要ありません。）
と2つの数字を書いて、\(\,\color{red}{足して-4}\,\)になるときどこにマイナスをつければ良いかを探すだけで良いですよ。
　\(\color{red}{\fbox{　＋2　　－6　}}\)
この数字の前に\(\,x\,\)をそれぞれつけて
　\(\,x+2\,\) \(\,x-6\,\)
（かっこ）をつけるだけです
　\(\,(x+2)(x-6)\,\)　

さいころ2つは表

問2　2つのさいころを投げたときの確率です。
確率は樹形図ですべて答えが出ます。
ただし、さいころ2つの場合は表がはやいです。
なぜさいころ2つのときだけ樹形図で押し通さないのか？

さいころ2つの問題が多いからです。

樹形図で良いですよ。
たいして時間はかかりませんからね。

高校入試に限らず確率問題の場合それぞれの問題に【ルール】があります。
まずはそれを読み取ります。
この「ルール確認」（具体例を調べる）ことをしない人は確率を高い確率で落とします。

この問題のルールです。

2つのさいころ\(\,\mathrm{A,B}\,\)を投げて
　\(\,\mathrm{A}\,\)の出た目を\(\,a\,\)
　\(\,\mathrm{B}\,\)の出た目を\(\,b\,\)
とし、差\(\,a-b\,\)が2以下の自然数となる確率

注意点は2つ。
　2つのさいころの出た目の差ではなく、\(\,\mathrm{A}\,\)のさいころから\(\,\mathrm{B}\,\)のさいころを引くこと。
　その差が自然数であること。

例えば
　\(\,\mathrm{A}\,\)が\(\,1\,\)で\(\,\mathrm{B}\,\)が\(\,3\,\)の場合は\(\,1-3=-2\,\)
これは自然数ではないので条件に合いません。

問題によっては「差が2以下」という問題もあります。
その場合はどちらか大きい方から小さい方を引くことができるので上の例は条件を満たしますが、
ここでは\(\,a-b\,\)と決まっていますので条件は満たしません。

表は自分で書いてみて下さい。
覚え太郎カード『確率』Q5にある表です。

ここでは条件で書き出してみます。
　\(\,a＞b\,\)　と　\(\,a-b≦2\,\)
が条件なので差が2以下となるのは
（\(\,a\,\)は\(\,b\,\)より大きくないと差が自然数になりません。）
　\(\,a=1\,\)　のとき差が自然数になる\(\,b\,\)はありません。　
　\(\,a=2\,\)　のとき　\(\,b=\color{red}{1}\,\)
　\(\,a=3\,\)　のとき　\(\,b=1,\color{red}{2}\,\)
　\(\,a=4\,\)　のとき　\(\,b=2,\color{red}{3}\,\)
　\(\,a=5\,\)　のとき　\(\,b=3,\color{red}{4}\,\)
　\(\,a=6\,\)　のとき　\(\,b=4,\color{red}{5}\,\)
だけです。
　\(a-b\)　の値が\(\,2\,\)となるのは　黒字の\(\,4\,\)通り
　\(\color{black}{\fbox{　ア　}}=\underline{　4　}\)

　\(a-b\)　の値が\(\,1\,\)となるのは　赤字の\(\,5\,\)通り
なので　\(a-b\)　の値が2以下になる場合は
　\(4+5=9\)通り
　\(\color{black}{\fbox{　イ　}}=\underline{　9　}\)

2つのさいころの出方は全部で36通りあるので求める確率は
　\(\displaystyle \frac{9}{36}=\underline{　\frac{1}{4}　}\)

やってみれば答えはすぐ出ます。

表は自分で書いてもらいたいところですが、ここは会員じゃない人もいるので書いておきます。
一番左の縦の並びの赤字を\(\,\color{red}{a}\,\)として、一番上の横の並びを\(\,\color{blue}{b}\,\)とします。
中の黒数字は\(\,a-b\,\)の値です。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\color{red}{1} & \hspace{3pt}0\hspace{3pt}\, & -1 & -2 & -3 & -4 & -5 \\ \hline
\color{red}{2} & 1 & 0 & -1 & -2 & -3 & -4 \\ \hline
\color{red}{3} & 2 & 1 & 0 & -1 & -2 & -3 \\ \hline
\color{red}{4} & 3 & 2 & 1 & 0 & -1 & -2 \\ \hline
\color{red}{5} & 4 & 3 & 2 & 1 & 0 & -1 \\ \hline
\color{red}{6} & 5 & 4 & 3 & 2 & 1 & 0 \\ \hline
\end{array}\)

実際にはすべてを書き込まなくても答えは出ます。
\(\,0\,\)より右は必要ありません。
\(\,0\,\)も自然数ではないので必要ありませんが、境界として書き込んでおくと分かり易いですよね。

表でやった場合と比べてみて下さい。
表を使うと考えることないでしょう？
探すだけです。

三角形の面積は底辺と高さ

問3　作図の問題です。

\(\,△\mathrm{ABP}\,\)の面積がもっとも小さくなる円周上の点\(\,\mathrm{P}\,\)の作図です。

底辺\(\,\mathrm{AB}\,\)は固定されていますので、高さが一番小さくなるときを探します。
簡単に言えば円\(\,\mathrm{O}\,\)と辺\(\,\mathrm{AB}\,\)との一番近い点、です。
円の一番下ですね。
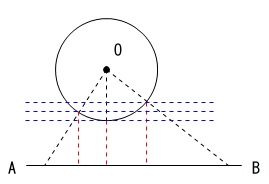辺\(\,\mathrm{AB}\,\)から円に平行に移動して、最初に円に触れるときが最小の高さになります。
つまりは円\(\,\mathrm{O}\,\)の接線と\(\,\mathrm{AB}\,\)が平行のときで、
円\(\,\mathrm{O}\,\)から\(\,\mathrm{AB}\,\)に垂線を下ろしたときの接点（円\(\,\mathrm{O}\,\)との交点）が点\(\,\mathrm{P}\,\)です。
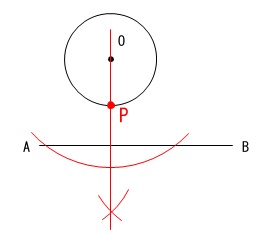円の中心から辺\(\,\mathrm{AB}\,\)に垂線を引いただけです。
点\(\,\mathrm{P}\,\)を示す記号を書くように指示があるので忘れずに書き込みましょう。

作図問題ではいろいろな線を書いてみて、
条件に当てはまりそうなものを見つけて、理由を見つけて作図に入れば良いです。
理由説明は必要無い場合が多いのでコンパスと定規とを使いまくれば見えてきます。

図形問題の基本

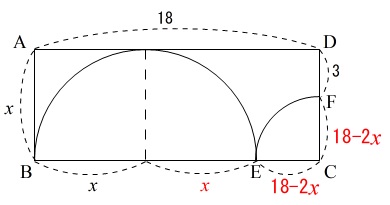
問4　長方形と円が書かれた図形問題です。
図形問題は図の中で考えるのですよ。
図の中で書き出せるだけ書き出せばほとんどの問題は終わっています。
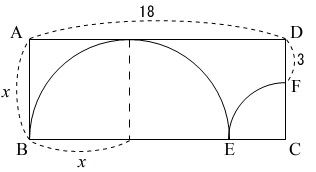長方形と半円と四分円があります。
方向性は2つありますので、問題の誘導してくれている方法でわかることを図の中に書き込んでいきましょう。
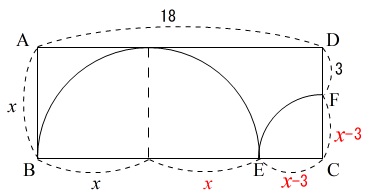　\(\,\mathrm{AB=DC}=x\,\)
なので
　\(\mathrm{CF}=\color{black}{\fbox{\(\, x-3 \,\)}}\)
また半径は等しいから
　\(\,\mathrm{CF=CE}=x-3\,\)
なので
　\(\,\mathrm{BC=BE+CE=AD=18}\,\)
だから
　\(\color{black}{\fbox{\(\,x+x+(x-3)=18\,\)}}\)
これを解けば半円の半径\(\,x\,\)が求まります。
　\(\begin{eqnarray}
x+x+(x-3)&=&18\\
3x-3&=&18\\
3x&=&18+3\\
3x&=&21\\
x&=&\color{black}{\fbox{　7　}}
\end{eqnarray}\)

ここでは先に　\(\,\mathrm{CF}=x-3\,\)　側から見ましたが、
四分円の半径は\(\,\mathrm{CE}\,\)でもあります。
\(\,\mathrm{BC=18}\,\)なので
　\(\mathrm{CE}=\color{black}{\fbox{\(\,18-2x\,\)}}\)
と半径はおくこともできますので、
　\(\,\mathrm{CF=CE}=18-2x\,\)
と
　\(\mathrm{AB=DC}=x\)
から
　\(\color{black}{\fbox{\(18-2x+3=x\)}}\)
という方程式も立てられます。